破运算之困 现课堂之彩——以 “直线与圆锥曲线综合”教学为例

李娟娟

(江苏省新海高级中学 222000)

美国著名的教育学家玻利维亚说过，掌握数学就是意味着要善于解题.这个“善于”是包含了掌握一定的解题方法，也涉及数学思想、数学运算技巧等诸多方面.因此，在课堂教学中，激发学生的兴趣，引导学生正确的思考，配以精准的运算，得出完美的解答结果是课堂追求的最高境界.下面以笔者在高三一轮复习课“直线与椭圆的位置关系”课堂实录为例谈谈数学运算在课堂中的渗透.

一、课堂实录

引入考试题，激发学生兴趣，引发学生的求知欲.

教师：对于直线与椭圆位置关系，我们已经有了一些认识，下面请思考这道题.

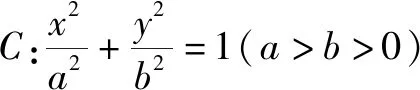
(1)求椭圆C的标准方程；

(2)设直线AP，BQ的斜率分别为k1，k2，是否存在常数λ，使得k1=λk2？若存在，求出λ的值；若不存在，请说明理由.

教师：知道离心率，知道焦点坐标，先请大家动笔完成第(1)题.

教师：概括简明扼要，明确基本量关系，运算准确.请思考第(2)问.

学生2：过右焦点F(1,0)的直线l与椭圆C交于P，Q两点，那么k1，k2的变化来源于这条直线，所以可以从设这条直线开始.

学生3：对，而且此直线要经过右焦点F(1,0)，设直线方程为x=my+1运算可能会简洁.

学生4：我认为还要补充说明一下若m不存在，直线PQ与直线AB重合，不合题意情况.

教师：嗯，说得不错，考虑直线的局限性，考虑到变化的根源，这样的话，此题思路清晰，方向明确，那就请动笔试试，从设出直线PQ开始找出正确答案吧！

(学生动笔做题，教师现场巡视，发现大部分学生在运算过程中停笔不前了)

教师板书：设P(x1,y1)，Q(x2,y2)，直线l的方程为x=my+1代入椭圆方程，得(4+3m2)y2+6my-9=0.

教师：这里请同学们注意，解题方向是消去x，在代入时，注意检查变量y前的系数及其符号，确保解答步骤准确，不影响下面解答.

但下面怎么处理？

(下面一片嘘声：对，对，我也算到这，下面怎么办？)

教师：注意观察特征，化简到最后y1与y2落单了，无路可走了.那么y1与y2有已有的联系能用上吗？如何借助已知的信息？

(教室一片安静，每位同学都在低头思考，用心演算)

学生6：既然y1与y2是方程的根，那么直接解出

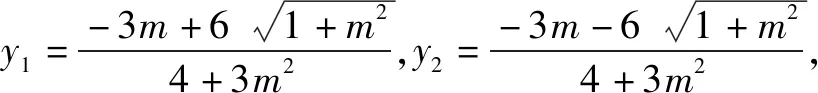
(教室爆发一阵热烈的掌声)

教师：真是山重水复疑无路啊，硬解恰恰是数学学习最本真的处理！

(学生们很兴奋，频频点头)

教师：嗯，紧扣目标，找到关系，转化到位，干得漂亮！

学生8：我是这样处理的(投影展示)

因为最终是一个比值，我估计能消去m，得到定值.

教师：太棒了，这是一个大胆的猜想，从最终结果是比值出发，那么猜测是否正确呢？

学生8：结果是对的，而且这个定值就是分子分母y2前的系数比！

教师：说得很棒，观察很到位.本题中运用不对称性来处理比值问题是一种常用方法，请大家在解过程中注意观察算式特征，大胆配凑，做到严格证明.

回到原题，请大家换个角度再想，有没有其他途径？

学生9：根据题意，如果利用k1，k2表示坐标P，Q，再借助三点F，P，Q共线，也应该能找到k1，k2关系.

众学生：对哦对哦，我怎么没想到！(教室响起一片掌声)

教师：特别好，看来这位同学对椭圆性质掌握很好，能熟练运用学过的知识解决新问题了.下面请大家选择其中一种方法落实问题.

(每位同学再次投入到紧张的演算中)

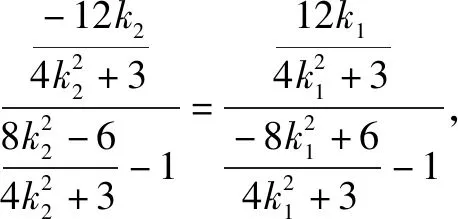
教师：两位同学思路清晰，书写流畅，运算准确，对比三种方法，大家总结一下本课的收获.

二、回顾与思考

教学中，正确运算是学生学习数学时必备和掌握的一项基本功.因此，本节课通过题目驱动，紧扣概念，由浅入深，第(1)题的设置解题方向明确，运算难度简单，目的是激发学生对解题的兴趣.第(2)题引导学生梳理关系，弄清算理，这节课的重点是运算的突破，引导学生冷静分析，更多的要培养学生的运算习惯，包括变量前系数与符号的检查习惯，抄写习惯，检验习惯等.

华罗庚说：“学数学而不练，犹如入宝山而空返.”数学课堂应该是一个有思考的课堂，更应该是一个有行动的课堂.在数学的课堂上教师不仅引导学生分析问题，也要强调运算过程的准确性，更需和学生一起面对运算结果的正确性，将运算渗透到课堂，将理论转化为实践，真正地让学生提高数学核心素养.