强降雨入渗下临海软土开挖边坡稳定性分析

2020-06-29黄泰坤王元战姜金勇贾晗刘少增

中国港湾建设 2020年6期

黄泰坤，王元战，姜金勇，贾晗，刘少增

（1.天津大学建筑工程学院，天津 300072；2.中交第一航务工程勘察设计院有限公司，天津 300222；3.南通港集团建设投资有限公司，江苏南通 226000）

0 引言

近年来我国频繁遭遇强降雨等极端天气，由此引发了较多的滑坡灾害事故[1-3]。季节性集中降雨具有强度大、持时长、次数多等特点，从而导致滑坡多，灾害重，产生严重的社会影响。工程中缺乏考虑强降雨对边坡稳定安全系数计算方法，常忽视降雨对边坡的影响，由于未采取排水措施，常在开挖交界面处出现开裂、冲沟等现象，严重影响了整体边坡的稳定性。

在强降雨过程中，土体内部多因素复杂的相互作用，土坡稳定性问题引起了工程师和学者的广泛关注。目前众多文献[4-10]集中于对原状边坡的原位浸水测试和增湿影响的室内试验；文献[11-15]采用数值方法和试验方法研究了路基边坡在雨水入渗后的开裂变形问题；文献[16-17]对某填沟造地工程进行了原位监测研究，表明地表积水和降雨影响入渗可达7 m 之多，但未对其他灾害现象进行探讨。上述研究黄土边坡、路基开挖中应用较多，为边坡理论和工程设计提供了大量支撑。然而针对软土、大面积开挖在强降雨入渗作用下边坡稳定性及其工程应用研究不多，其防控的设计方法与技术措施鲜有报导。

鉴于此，本文以某软土开挖工程实际为背景，基于ABAQUS 有限元软件平台，建立了工程区域非饱和土渗流-应力耦合模型，研究强降雨入渗边坡稳定性的影响及变形规律，为类似项目设计理论和工程措施提供一种很好的展示。

1 工程背景

某碱厂排渣场位于滨海浅滩边上，工程竣工后经多年碱渣堆积形成现有碱渣山，随着环保的加强及港口开发的需要，急需对碱渣山搬迁治理，设计方案为开挖填埋碱渣。纳渣区选址于碱渣山北侧大面积浅滩区域，场地标高+3.5 m，开挖底标高为-10.0 m，设计边坡1:3～1:4，开挖面积约70 万m2。设计了多级马道开挖（图1）。开挖深度大、土质软、后方堆载高碱渣山，施工过程需经强降雨期，为确保边坡安全，对降雨入渗下软土开挖边坡整体稳定性进行研究。

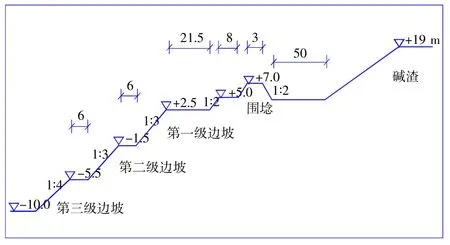
图1 软土开挖、后方围埝和已堆载的碱渣断面图Fig.1 Cross-section of soft soil excavation,rear enclosure and loaded slag

2 有限元数值模型建模方法

2.1 本构模型

土体本构模型采用Mohr-Coulomb 模型。

Mohr-Coulomb 准则是根据材料发生破坏时的应力Mohr 圆得到的，破坏线是与Mohr 圆相切的直线，Mohr-Coulomb 准则可表示为式（1）：

式中：τ 为材料的剪切强度；σ 为该点的应力；c为材料的黏聚力；φ 为材料的内摩擦角。

Mohr-Coulomb 准则采用应变不变量表示时屈服面方程为式（2）～式（4）：

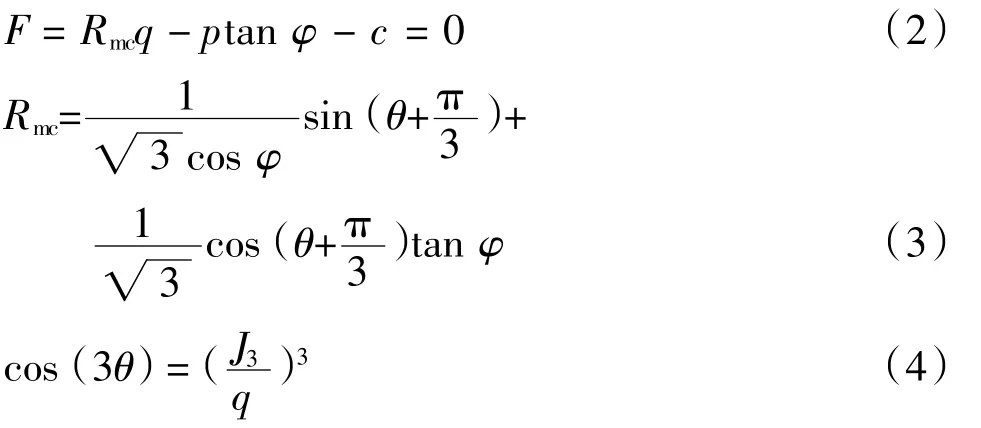
式中：p 为球应力；q 为广义剪应力；φ 为岩土体材料的内摩擦角，取值范围为[0，90°）；c 为土体黏聚力；Rmc（θ，φ）为M-C 偏应力系数，它决定平面内的屈服面形状；θ 为极偏角；J3为第三偏应力不变量。

2.2 非饱和渗流

饱和土体采用常规达西渗流理论。非饱和土中，由于有水和气两种流体存在于渗流中，与饱和土的流动性质不同。Richards[18]于1931 年忽略气体流动阻力，将Darcy 定律推广到非饱和土，该定律采用层流式的Darcy 定律表示，如式（5）：

式中：θw为含水率；k（θw）为某一体积下含水率 θw的非饱和土渗流系数。

在非饱和土体中，由于部分孔隙水被气体所填充，其渗透性小于饱和透水性，同时，又由于受土体含水率、饱和度或孔隙比变化影响，因此将渗透系数表示为基质吸力、饱和度S 和体积含水量 θw的函数 k（θw）。

2.3 降雨入渗模型

降雨入渗的过程复杂，Mein 和Larson[19]采用由降雨强度q、土壤允许入渗的容量fp、土壤饱和时的渗透系数ks等3 个因子来描述降雨入渗的过程与行为：

1）q ＜ks时，地表径流不会发生，降雨将全部入渗，此时水的入渗率保持不变。

2）fp＞q≥ks时，所有的雨水全部入渗，随着入渗深度的增加而变小，但此时降雨强度还未达到土壤允许入渗的容量，故入渗率并不会降低，且入渗率很高。

3）q≥fp时，由于降雨强度大于土壤的入渗容量，故部分降雨并不入渗，形成地表径流，而入渗率在降雨达到入渗容量后，将逐步下降。

所以，降雨入渗过程可以分成为2 个阶段，第一阶段称为供水控制阶段，第二阶段称为土壤入渗率控制阶段。2 个阶段的交点称为积水点。前一阶段称为无压入渗或自由入渗，后一阶段称为积水或有压入渗。本文中，降雨考虑为强降雨情况（＞10 mm/h），远大于土体渗透能力，因此，本模型中的降雨入渗为“积水模型”或有压入渗，即第3 种情况。

2.4 强度折减法

强度折减法SSRT（Shear Strength Reduction Technique）最早由 Zienkiewicz 等[20]提出，后被许多学者广泛采用。当假定边坡内所有土体抗剪强度的发挥程度相同时，这种抗剪强度折减系数相当于传统意义上的边坡整体稳定安全系数Fs，又称为强度储备安全系数，与极限平衡法中所给出的稳定安全系数在概念上是一致的。

折减后的抗剪强度参数可分别表达为式（6）、式（7）。

式中：c 和φ 为土体所能提供的抗剪强度；cm和φm为维持土体平衡所需要的或土体实际发挥的抗剪强度；Fr为强度折减系数。

计算中假定不同的强度折减系数Fr，根据折减后的强度参数进行有限元分析，观察计算是否收敛。整个计算过程中不断的增加Fr，当达到临界破坏时的强度折减系数Fr就是边坡稳定安全系数Fs。

3 有限元数值模型建立与验证

3.1 模型构建

根据上述模型建立方法建立本工程有限元二维边坡稳定性分析模型（图2）。其中，模型底部为固定位移约束（U1=U2=0），两侧为水平位移约束（U1=0）；模型两侧的孔压按静水水压条件布置，左侧水位标高为-10 m，右侧水位标高为+3.5 m。图2 中的围埝为碾压黏土，碱渣山为碱渣，土体自上而下分别为：淤泥质粉质黏土、淤泥质黏土、淤泥、粉质黏土、粉土、粉质黏土和粉土，在图2 中用不同颜色标记。土体的本构模型采用Mohr-Coulomb 模型，孔隙水流动按扩展的非饱和达西定律考虑。

图2 有限元模型Fig.2 Finite element model

土层分布以及土体材料参数如表1 所示。

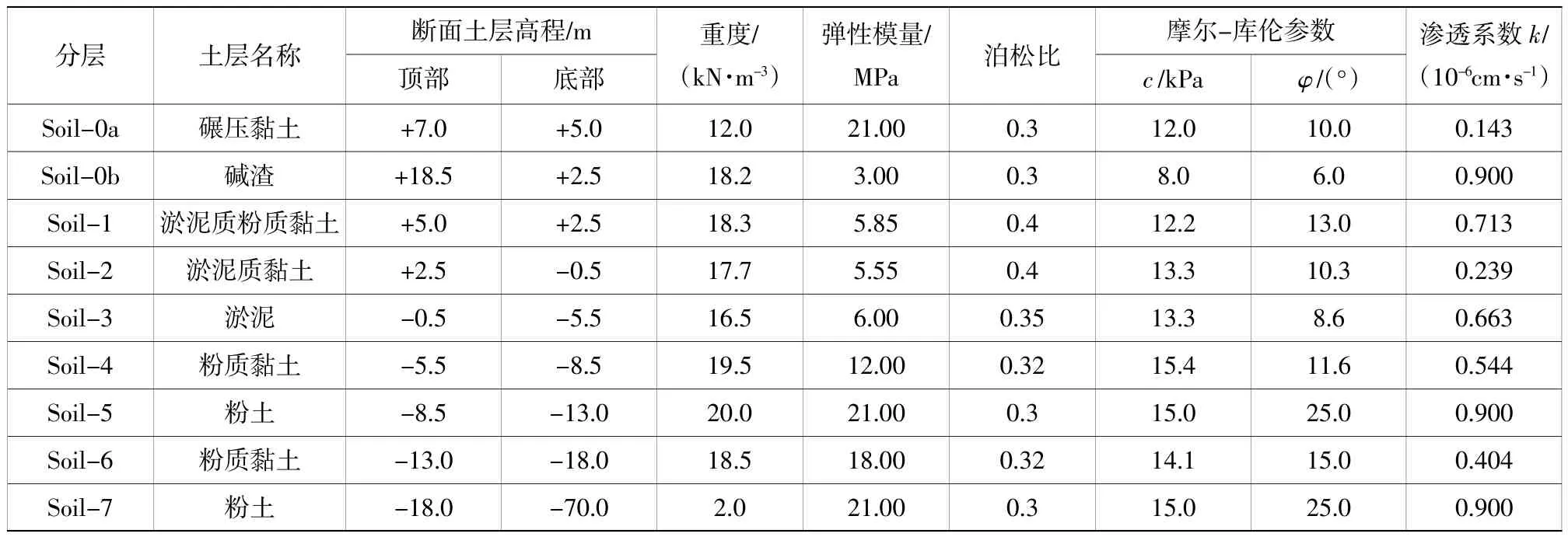
表1 土层分布及土体材料参数Table 1 Soil layer distribution and soil material parameters

3.2 模型验证

图3 为野外现场一级开挖断面（坡肩）处的监测水平位移与有限元计算结果对比。有限元计算结果与监测数据相比略大，但总体上得出的计算结果和监测数据较为接近。

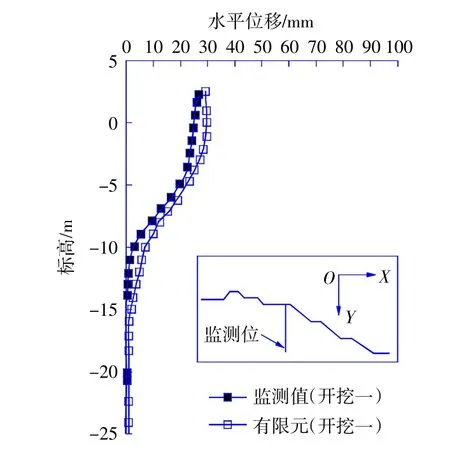
图3 有限元计算结果与现场监测数据的对比Fig.3 Comparison between the results of FEA and field monitoring date

图4 为未考虑雨水入渗影响下，GEO-SLOPE软件的极限平衡法边坡稳定性计算结果，其中，水位考虑为两段折线，土层参数与有限元模型中的设置一致。计算结果表明，最不利边坡安全系数为1.657，与本文建立的有限元计算结果1.70相近。

图4 GEO-SLOPE 极限平衡法边坡稳定性Fig.4 Slope stability of limit equilibrium method based on GEO-SLOPE

4 有限元数值模型应用

4.1 模型设置

基于实际开挖工程，分别研究常规不考虑强降雨影响、考虑强降雨入渗影响的开挖边坡稳定性。模型设计2 种工况，即工况一：不考虑雨水入渗影响；工况二：考虑强降雨入渗影响。

4.2 模拟结果

4.2.1 不考虑雨水入渗（工况一）

图5 为开挖边坡顶处位移与折减系数的关系曲线。从图中可以看出，无论是哪一种失稳准则，工况一的安全折减系数都为1.70。

图5 U-Fr 曲线图Fig.5 U-Fr curve

图6 为不考虑雨水入渗影响下的边坡稳定（工况一）的孔隙水压力POR（总孔压）、土体饱和度SAT、土体水平位移U1、竖向位移U2，以及破坏时的塑性应变PEMAG 变化特征图。

图6 工况一边坡响应特征图Fig.6 Response characteristic of slope of condition 1

如图6 所示，未折减之前，边坡顶处土体水平、竖向位移分别为-0.030 m、+0.067 m，在达到滑移破坏阶段，二者位移分别达到-1.35 m 和-0.56 m。从破坏时塑性应变图可以看出，未考虑雨水入渗，滑裂面滑出点位于坡底-10 m 位置。

4.2.2 考虑强降雨入渗（工况二）

图5 为开挖边坡顶处位移与折减系数的关系曲线。从图中可以看出，无论是哪一种失稳准则，工况二的安全折减系数都为1.42。

图7 为考虑雨水入渗影响下的边坡稳定（工况二）的孔隙水压力POR（总孔压）、土体饱和度SAT、土体水平位移U1、竖向位移U2，以及破坏时的塑性应变PEMAG 变化特征图。如图所示，未折减之前，边坡顶处土体水平、竖向位移分别为-0.250 m、+0.087 m，在达到滑移破坏阶段，二者的位移分别达到-4.48 m 和-1.38 m。考虑雨水入渗，滑出点位于坡面-5.5 m 位置，较工况一有所抬高，提示坡面可能出现破坏情况。

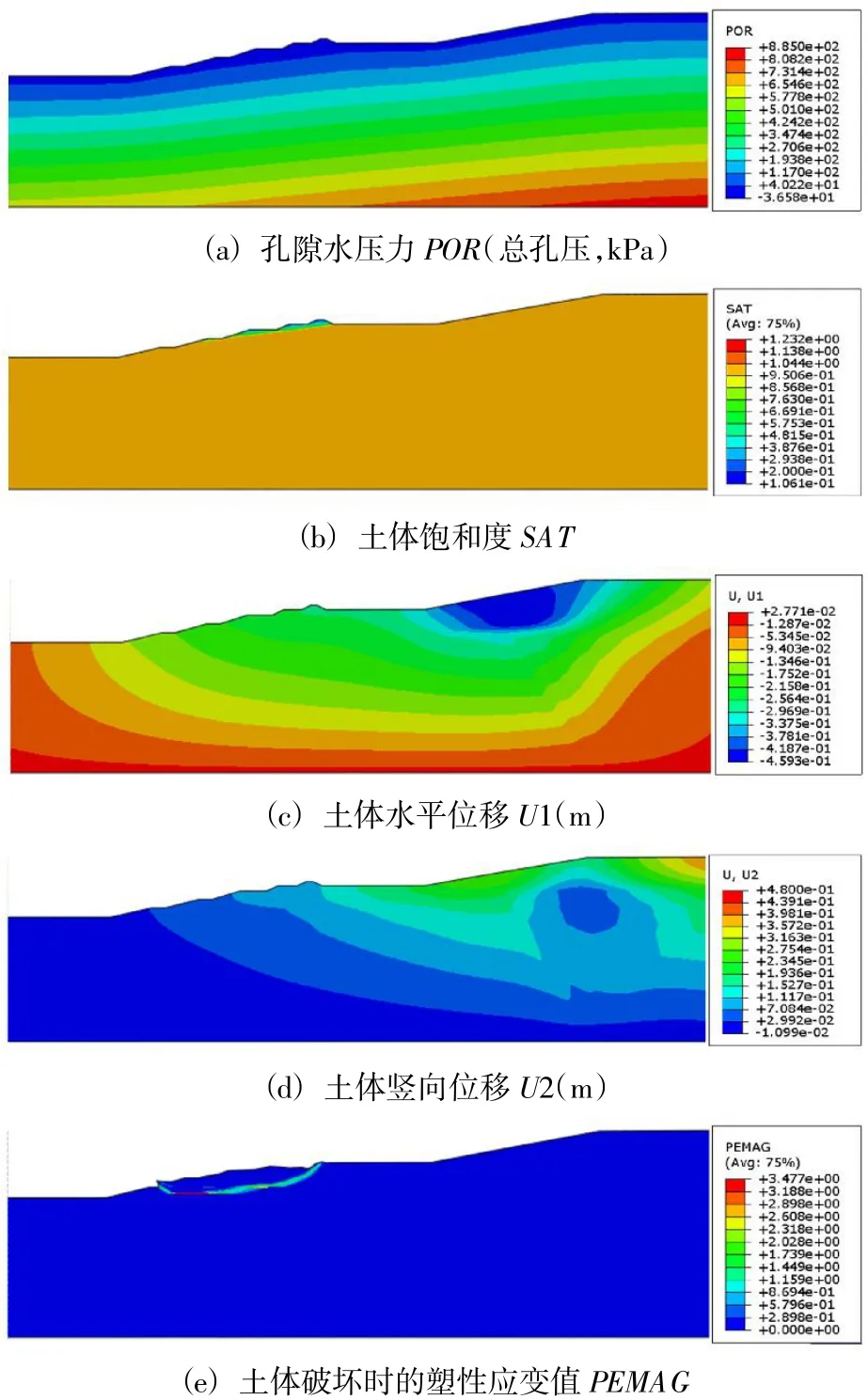
图7 工况二边坡响应特征图Fig.7 Response characteristic of slope of condition 2

4.3 计算结果讨论

1）安全系数及位移

表2 为两种计算工况下，边坡稳定安全系数，水平位移U1、竖向位移U2。从表中对比可以看出，随着雨水入渗，边坡稳定安全系数由1.7 降至1.42，降低16.5%。水平位移由0.03 m 提高到0.25 m，大幅度增加可能的破裂宽度。需要指出的是，本文采用有效应力法计算，得到的安全系数可直接用于指导工程设计，避免了总应力法计算值偏低造成的设计过于保守。

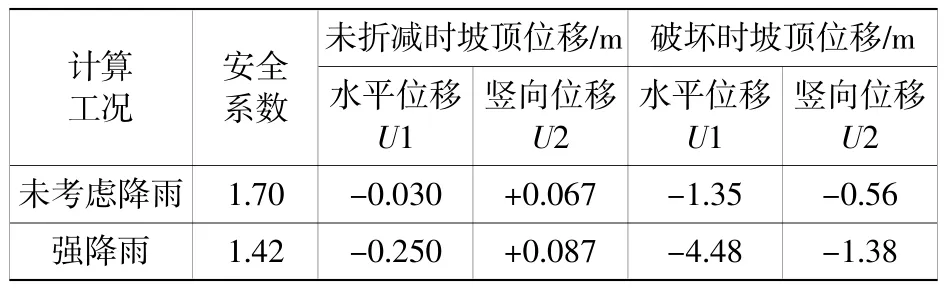
表2 不同工况下边坡安全系数及坡顶位移Table 2 Slope safety factor and slope top displacement under different conditions

2）浸润线

根据两种工况对应的边坡孔压（POR）、饱和度（SAT）分布图（图6～图7）。由计算结果可以看出，在降雨入渗区域，孔压会随着降雨强度的增大而增大。同时，该部分区域的土体孔隙趋向于饱和，从而使得浸润线往上移动。出现这种情况的原因是：土体渗透系数较小（0.512 4～3.24 mm/h），在强降雨（＞10 mm/h）入渗情况下，降雨强度远大于土体渗透性，使得地表形成积水，降雨变现为“积水模型”或有压入渗，入渗强度取决于土体渗透性，而不是降雨强度。

后期工程实际中经历了强降雨过程，并出现局部开裂现象，但未出现滑坡等整体稳定问题，表明设计边坡是合理的。研究成果为工程设计与实际施工提供了指导，也可为同类工程提供参考。