独塔双索面混凝土斜拉桥地震响应分析

2020-06-29莫海洪饶梓彪

中国港湾建设 2020年6期

莫海洪，饶梓彪

（中交第四航务工程勘察设计院有限公司，广东广州 510230）

0 引言

近年来，除了当前尚处于研究和争论状态的基于失效概率的地震功率谱抗震设计和虚拟激励分析法外，基于静态水平力加载的加速度反应谱方法和基于动力学基本规律的时间历程分析法是当前桥梁工程抗震设计中普遍应用的两种成熟设计方法[1-2]。反应谱方法通过分析结构本身的振动特性，将实际复杂结构抽象为一个具有有限自由度的力学模型，并基于矩阵解耦的数学方法，将多自由度系统分解为一组具有统计相关性的单自由度系统。通过理论解析技术分别计算得到每个单自由度系统的动力学响应后，再将各单自由度系统的响应结果进行统计学叠加，作为整体结构在地震作用下的最终响应结果；地震时间历程动力分析法对计算时间间隔进行离散，并在每个离散的时间步长内对结构应用动力学基本方程进行动力响应计算[3-4]。时间历程动力分析法是到目前为止计算地震动力响应的最完整分析方法，该方法可以在计算过程中考虑各种不同的非线性动力学效应，但由于运算过程的复杂性和计算资源的开销巨大，因此时间历程分析法一般只是作为反应谱分析的验证手段[5-6]。

本文以酉水三桥为依托工程，对其动力特性及抗震性能进行了分析。如前所述，为校验分析方法和分析结果的准确性，计算分别采用加速度反应谱分析法与时间历程分析法进行独立计算并比对计算结果[7]。地震响应计算主要针对桥体主墩和桥身主梁的特征截面进行地震响应分析，并将基于数值分析得到的结构响应结果与CJJ 166—2011《城市桥梁抗震设计规范》[8]中所推荐的拟静力方法计算结果进行比较，从而全面评估桥梁在地震作用下的结构可靠性。本文研究的中间数据与所得到的结论对于其他桥梁工程的抗震评估具有一定的参考价值。

1 工程概况

酉水三桥全长417 m。其中桥体主结构为独塔双索面斜拉桥，桥梁主墩和主梁之间设计为固结传力模式。桥梁主体斜拉部分的跨径长度组合为196 m+101 m+62 m，引桥采用2×25 m 小箱梁，桥面宽度设计为29.5 m。桥梁主塔结构设计为钻石形，桥体主梁结构设计为三室单箱预应力混凝土结构，斜拉索布置设计为扇形。主桥结构立面如图1 所示[9]。

图1 桥梁立面布置图（m）Fig.1 Elevation layout of bridge(m)

2 抗震设防标准及结构抗震性能目标的确定

根据GB 18306—2015《中国地震动参数区划图》[10]及 JTG B02—2013《公路工程抗震规范》[11]中对于地震场地分类的相关规定：通过前期工程地质勘察，可以判断工程场地土类型属中硬土，场地类别归属为Ⅱ类，工程场地的地震基本烈度为6 度，对应的地震动峰值加速度为0.05g，场地特征周期值为0.35 s，综合信息表明，工程场地属于地震不利区。本文依托工程所处的场地在不同超越概率条件下对应的地表水平加速度峰值如表1 所示。

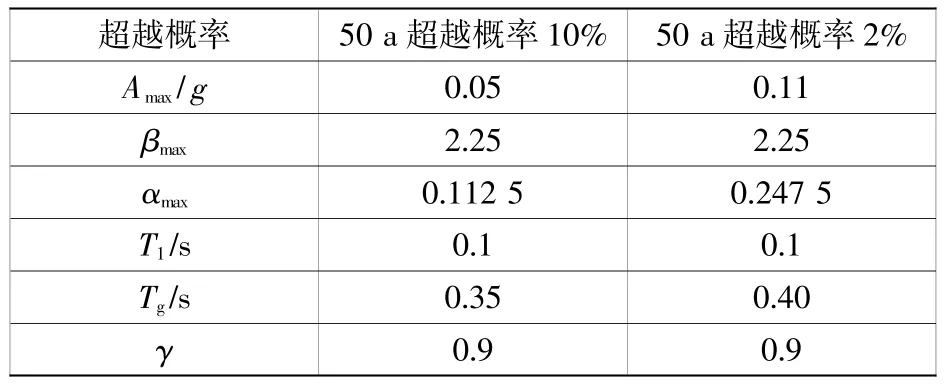
表1 工程场地地表设计地震动参数Table 1 Design ground motion parameters of engineering site

根据《城市桥梁抗震设计规范》[8]中的相应规定：对于斜拉索结构的市政类桥梁，其抗震设防级别应设置为甲级，其抗震标准应高于基本场地烈度1 度，因此考虑桥梁结构的抗震设防标准应当有所提高，见表2。

表2 桥梁主体结构的抗震设防标准与性能目标Table 2 Seismic fortification standards and performance objectives of bridge main structure

3 计算模型与动力特性

3.1 计算模型

计算分析采用MIDAS 桥梁结构专用有限元程序软件。采用空间梁单元模拟桥梁结构的桥墩、主梁和主塔结构，采用桁架单元模拟斜拉索对主梁的连缀效应，并以此模型为基础，开展桥梁整体结构在地震作用下的动力响应评估。

3.2 边界条件

本桥成桥状态结构边界条件边、中支点支座模拟弹性连接，考虑交界一联桥梁刚度边界条件影响，桩基础采用“m”法土弹簧模拟[12-13]。

3.3 动力特性

采用多重Ritz 法对全桥动力特性进行分析，成桥状态振型特点见表3。

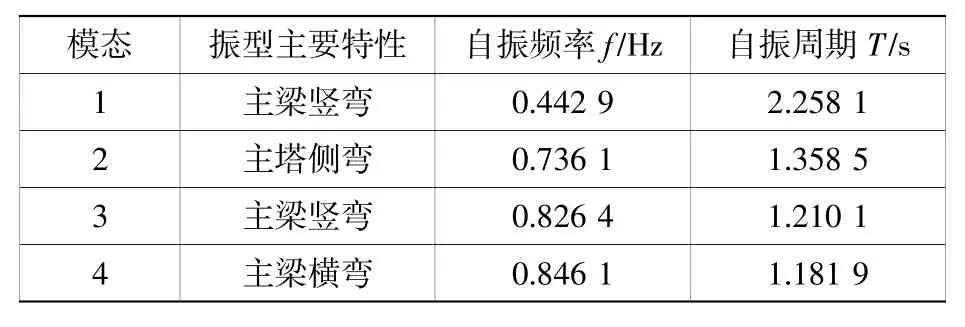
表3 成桥状态结构动力特性Table 3 Dynamic characteristics of bridge structure

4 地震反应谱分析

4.1 结构时间历程分析

与加速度反应谱分析类似，时间历程分析中的地震动输入采用水平纵向+竖向以及水平横向+竖向两种组合方式。

根据《城市桥梁抗震设计规范》[8]中的相关规定，在考虑竖向地震加速度的组合作用下，竖向加速度峰值取为水平向加速度峰值的2/3。为尽可能消除时间历程计算结果的随机性，主桥结构的地震响应计算结果取3 组随机地震波作用结果的最大值。基于上述计算条件，桥梁主体结构在E2地震作用下的位移响应如表4 所示，桥梁主塔结构的控制截面的地震响应结果如表5 所示（仅列举E1 地震作用下的响应结果）。

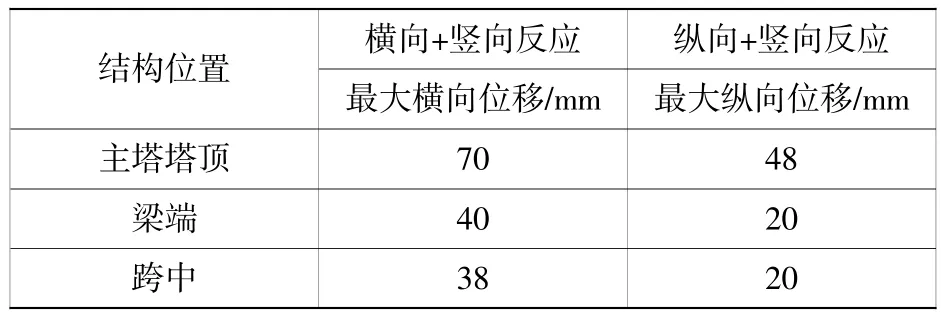
表4 桥梁控制点处地震位移响应（E2 地震作用）Table 4 Seismic displacement response at bridge control point(E2 seismic action)

表5 主塔结构（控制截面处）地震响应（E1 地震作用）Table 5 Seismic response of main tower control section(E1 seismic action)

4.2 结构反应谱分析

根据《城市桥梁抗震设计规范》[8]中的相关规定，采用加速度反应谱进行地震响应分析时，所选用的加速度反应谱为Sa（T）=Amaxβ（T），其中：β为加速度放大系数谱，是场地周期T 的函数；βm为加速度放大系数的最大值；Tg为工程场地的特征周期，s；γ 为反应谱下降段的衰减指数，当系统阻尼比为0.05 时，该值为0.9；Amax为场地的地面加速度峰值。本文计算所采用的参数见表6。

抗震分析中通常需要考虑水平方向的地震加速度与竖直方向地震加速度的联合作用。水平向的地震作用通常按照纵向和横向分开考虑，因此地震激励的输入方式分为两种：1）水平纵向+竖向； 2）水平横向+竖向，不同方向地震作用结果采用SRSS 法组合。

表6 场地水平向设计反应谱特征参数（阻尼比5%）Table 6 The characteristic parameters of horizontal design response spectrum of site(damping ratio 5%)

对于地震响应分析而言，需要确保有足够多的模态参与到计算中，从而避免遗漏重要的结构响应。通过试算可以确定前150 阶振型在各自由度上的质量参与系数均达到95%以上。不同振型计算结果采用CQC 法组合。从结构反应谱分析与结构线性时程分析两种方法计算得到的结果比对可以看到：不管是对于结构位移响应还是结构内力响应，反应谱法和时间历程法的计算结果都较为接近，总体而言，时间历程法计算结果在量值上偏大，两者相对误差不大于20%。

4.3 结构抗震验算

通过以上分析可以看到：时间历程分析法的计算结果相对加速度反应谱方法的计算结果略大，因此本节采用线性时程分析法的计算结果对结构抗震性能进行校验，以判断结构是否满足抗震性能规定。

钢筋混凝土截面等效屈服弯矩在实际加载过程中并无明显的指标可供参考，在实际实施过程中通常将实际的截面弯矩-曲率曲线等效为一个弹塑性曲线。对应的等效屈服弯矩Meq计算如图2由阴影部分面积相等求得。其中My为截面在指定轴力作用下的外层钢筋屈服时所对应的弯矩；Meq=My为所对应的等效屈服弯矩；Mu对应指定轴力作用下的截面抗弯承载力。基于上述方法，主塔的抗震验算结果见表7。

图2 等效屈服曲率和屈服弯矩计算图示Fig.2 Calculation diagram of equivalent yield curvature and yield moment

表7 最不利轴力下主塔初始屈服弯矩验算（E2 地震作用）Table 7 Checking calculation of initial yield moment of main tower under the most unfavorable axial force(E2 seismic action)

从表中可以看到：在E2 地震荷载作用下，桥梁主塔结构最不利截面弯矩安全系数均大于1，说明桥梁主塔结构仅发生可轻微损伤，满足抗震性能要求。