深水空心矩形高墩地震动水附加质量计算方法研究

毛穗丰，高立宝，徐章洁

(中国电建集团成都勘测设计研究院有限公司，四川 成都 610072)

近年来，为开发丰富的水电资源，我国西部山区修建了大量水电站。随着水库的蓄水，原本跨越山区的陆地桥梁变成了深水桥梁，这些桥梁桥墩的入水淹没深度取决于桥跨布置及水库的蓄水深度，少则几十米，多则上百米。如小湾水电站库区的漭街渡大桥，桥墩高168 m，入水深度达166 m；紫坪铺水库的庙子坪大桥，桥墩高102 m，入水深度达85 m；已建成通车的雅江两河口水电站库首特大桥，桥墩高172 m，入水深度达167.84 m，为目前世界桥梁淹没最深的深水桥梁。

我国是一个地震多发的国家，一旦发生破坏性的大地震，将造成巨大的经济损失和人员伤亡，而桥梁工程是公路交通系统中最容易受到地震损伤的环节。如在汶川地震中，岷江紫坪铺水电站库区的庙子坪大桥发生主墩墩底开裂、引桥简支梁掉落等震害，造成了交通中断，严重影响抗震救灾。由于桥墩开裂出现在深水的墩底，水下修复作业困难，为此进行的维修加固花费了大量资金，且耗时近一年之久。可见，深水高墩桥梁的抗震问题不容忽视。

与陆地桥梁不同，深水桥梁长期淹没在水中，当桥墩自身发生振动时，也会引起桥墩周围水体的耦合振动，这种桥墩-水耦合效应会延长结构自振周期，放大地震作用下的结构响应，增加结构失效的概率[1-3]，是深水桥梁地震响应分析中必须考虑的重要因素。现阶段，桥墩-水耦合效应可通过解析方法、流固耦合数值模拟、附加质量等方式进行考虑计算。其中，附加质量方法最早由Westergaard研究大坝在地震作用下的动水压力问题时提出[4]，后经Morison方程推导得到。该方法将动水作用力转化为附加质量的惯性力，具有概念清晰且易于在有限元分析中实现的特点，已被多个抗震设计规范所采用。如我国《铁路工程抗震设计规范》[5](以下简称“铁路规范”)、日本《道路桥示方书·同解说，Ⅴ耐震设计编》[6](以下简称“日本规范”)、欧洲《Eurocode8》[7](以下简称“欧洲规范”)。

目前，空心矩形桥墩是一种广泛使用的深水桥墩形式，而抗震设计规范给出的动水附加质量计算方法主要是针对圆形实体桥墩，对矩形桥墩的适用性尚不明确；对空心桥墩箱室内域水影响如何考虑未明确；对深水下超高桥墩的实用可靠性不明确；对深水下超高桥墩受水流、波浪影响情况不明确。以上问题在现有文献中也鲜有介绍，因此，对于深水桥梁的抗震问题需要开展深入研究。

1 背景项目简介

国道G317线红旗大桥(见图1～2)位于四川省大渡河双江口水电站水库区内白湾乡附近，横跨足木足河谷，连接马尔康市和壤塘县。红旗大桥主桥为120 m+220 m+120 m预应力混凝土连续刚构，引桥为简支梁和连续梁组合结构，桥梁全长758 m，桥面宽13 m。该桥最大桥墩高度为172 m，桥墩截面形式为矩形空心箱型，墩顶截面外轮廓尺寸为11.0 m×7.0 m，墩底截面外轮廓尺寸为13.04 m×12.734 m。双江口水电站库区蓄水后，足木足河水位大幅上涨，主跨桥墩在使用期间几乎完全浸没在水中，在地震作用下，深水桥墩-水体耦合效应显著。鉴于红旗大桥在经济、交通等方面占据的重要地位，以及红旗大桥深水、大跨、高墩的特殊性，因此相关人员开展了对红旗大桥抗震性能的专题研究。这不但能保证大桥在寿命期内的抗震安全，而且对我国深水多跨连续刚构桥梁的抗震研究具有重要的指导意义。

图1 红旗大桥(水库蓄水前效果)

图2 红旗大桥(水库蓄水后效果)

2 水下振动台试验

动力模型试验不仅是研究深水桥梁结构抗震设计理论的重要方法，也能更真实地反映深水桥梁在地震作用下的动力性能，为进一步的理论研究提供可靠的数据和信息支撑。为揭示地震发生时红旗大桥在地震、波浪和水流联合作用下动力响应规律，相关人员进行了红旗大桥缩尺模型水下振动台试验。

2.1 试验系统

水下振动台试验在大连理工大学海岸与近海工程国家重点实验室进行。该试验系统的波流水槽长、宽、深分别为21.6 m、5.0 m和1.0 m，工作水深为0.2～0.8 m，振动台工作区尺寸为4 m×3 m，满载荷载质量为10 000 kg，可以进行水平向振动、竖向振动以及平面内摇摆振动试验。水池一端是推板式造波系统和造流系统，试验波浪最大波高为0.33 m，试验波浪周期为0.5～4 s；试验水流最大流速(水深0.4 m)大于0.5 m/s，试验水流最大流量为1.0 m3/s。

2.2 试验模型

本试验选用有机玻璃(聚丙烯树脂)作为模型材料，选取铅块作为配重材料。模型比例1:220，将桥墩模型分成若干节段，分别加工制作，桥墩设置排水孔，允许水进入桥墩内部。将制作完成的各节段试块在钢板上逐层拼装，模型底部与钢板、钢板与振动台之间均通过螺栓连接固定。试验模型见图3～5。

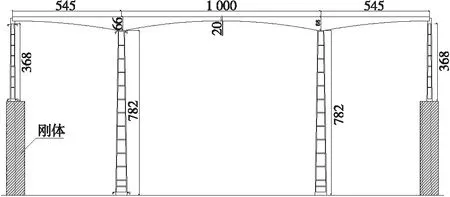
图3 缩尺模型(单位：mm)

图4 水下振动台模型(无水)

图5 水下振动台模型(正常蓄水位)

2.3 试验地震波选取

为了考察深水桥梁结构在不同地震、波浪和水流作用下的性能，综合考虑原型所处场地的地质情况和本次动力试验的加载特点，选用三组地震加速度时程曲线：一条是按实际场地情况，根据规范加速度反应谱生成人工模拟的加速度时程曲线；一条是在工程设计和理论分析中应用较广泛的实际强震记录El-Centro波；另一条是离本试验原型场地较近且造成破坏较大的汶川波。

2.4 试验工况

工作人员分别输入人工波、EI-Centro波、汶川波三种地震波，设定0.1 g、0.15 g、0.2 g三种不同峰值加速度，在无水、死水位及正常蓄水位三种水位状况下，以最大水流速度0.27 m/s、波浪高0.042 m、波浪周期0.5 s进行试验。

2.5 试验结论

通过深水高墩连续刚构桥梁全桥模型的水下振动台及地震、波流联合作用试验，研究库区深水桥梁在地震、波浪和水流联合作用下的结构响应，探讨不同因素对深水桥墩地震响应的影响规律，得到如下主要结论：

(1)水的存在会降低深水桥墩的自振频率。

(2)在峰值加速度0.2 g的地震作用下，红旗大桥桥梁模型处于弹性工作阶段，未发生开裂损伤。根据弹性相似比尺关系，可以认为在峰值加速度0.26 g的地震作用下，原桥结构处于弹性阶段。

(3)在地震、波流、水流耦合作用下，桥墩各测点加速度响应、动水压力与地震单独作用差异较小，说明库区深水高墩桥梁的结构响应由地震作用主导，波浪和水流作用的贡献相对较小，对结构响应不起控制作用；同时考虑到库区深水桥梁的工作特点，在库区深水高墩桥梁地震响应计算时可忽略波流和水流的作用。

(4)横桥向地震作用下，水位对各测点加速度响应及桥墩墩中加速度响应均大于墩底，同时，桥墩中部的加速度最大值均表现为在死水位下最大，无水次之，正常蓄水位最小。桥墩的动水压力最大值受水位影响显著，受地震波峰值加速度的影响不明显，正常蓄水位下桥墩的动力压力最大值均大于死水位。

(5)桥墩的动力压力受不同波形的影响很小。

(6)由于桥梁纵桥向刚度较大，在纵桥向地震作用下，纵桥向响应峰值较横桥向加载时偏小，相同水位及地震动峰值加速情况下，桥墩纵桥向动水压力最大值比横桥向小很多。

3 动水附加质量计算方法

附加质量法已在多国规范中采用，但仍未明确除圆形截面以外其他截面的计算方法，也未明确截面内域水的考虑方法。本文提出同时考虑桥墩内外域水影响的矩形截面动水附加质量计算方法，并以此方法建立高效有限元数值模型与水下振动台模型的动力特性比对；另外，建立基于势流体理论的精细化数值模型与有限元数值模型比对地震响应，以验证附加质量方法的准确性。

3.1 各国规范动水附加质量计算方法

3.1.1 铁路规范

对于圆形或圆端形桥墩，水中桥墩高度z处的单位墩高的附加质量为：

(1)

式中，mw(z)为桥墩单位高度的附加质量，kg/m；hw为水深，m；ρw为水的密度，kg/m3；A为桥墩高度1/2处的截面面积，m2。

3.1.2 日本规范

对于周边完全由水包围的柱状桥墩，距墩底z处单位墩高的附加质量为：

(2)

式中，mw(y)为距水面深y位置处的单位墩高附加质量，kg/m；A为桥墩的截面积，m2；b为地震时垂直于动水压力作用方向的桥墩尺寸，m；a为地震时平行于动水压力作用方向的桥墩尺寸，m；hw为水深，m。

3.1.3 欧洲规范

对于直径为D圆形截面桥墩，单位墩高附加质量即为单位高度的桥墩所排开水的质量[9]：

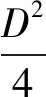
(3)

3.1.4 各规范方法附加质量沿墩高分布

对于深水空心矩形桥墩，根据三种规范得到外域水附加质量沿墩身的分布情况，如图6所示。由图6可知，铁路规范规定的附加质量沿墩高呈双线性分布，在80%水深以下部分沿墩高不变，在80%水深以上部分随墩高增大线性减小至零。日本规范规定的附加质量沿墩高呈抛物线变化，在墩底位置最大，随墩高增大逐渐减小至零，附加质量整体上较铁路规范、欧洲规范偏小。欧洲规范规定的附加质量沿墩高为固定值，与铁路规范在80%水深以下的附加质量相同。

图6 各规范附加质量沿墩高分布

3.2 空心矩形桥墩动水附加质量计算方法

当空心矩形桥墩设置在深水中时，为平衡桥墩内外的静水压力，通常在桥墩壁上设置进水通道，允许水进入空心桥墩内部，所以在静水压力作用下，深水空心桥墩的内部存在一定量的水，且水位与桥墩外部水相同。在地震作用下，桥墩内外部的水体均会对桥墩产生动水作用，因此在分析深水空心矩形桥墩的地震响应时，应同时考虑内外水的附加质量[8]。

3.2.1 外域水附加质量计算

对于矩形桥墩外域水动水附加质量，通常根据矩形桥墩在振动时的迎水面宽度D(即垂直于振动方向的截面宽度)，等效成直径为D的圆形桥墩，然后根据现有针对圆形截面的计算方法得到该圆形桥墩的附加质量，再乘以修正系数KC，最终得到矩形桥墩的动水附加质量[9]，矩形截面等效示意见图7。修正系数KC是矩形桥墩长宽比的函数，挪威船级社(DNV)[10]、欧洲规范[7]给出了不同长宽比D/B对应的KC值，如表1所示。为便于工程应用，杨万理[9]根据表1所示的离散数据点进行拟合，得到KC的拟合公式，如式(4)所示。该式可用于计算0.1≤D/B≤10范围内矩形桥墩的修正系数KC，能够涵盖工程中常见的矩形桥墩尺寸。

KC=1.51(D/B)-0.17

(4)

根据上述过程，空心矩形桥墩外域水单位高度动水附加质量计算公式可以表示为：

mout=1.51(D/B)-0.17mw

(5)

式中，mw为直径等于D的圆形桥墩单位高度附加质量，可根据式(1)～(3)进行计算。

3.2.2 内域水附加质量计算公式

空心桥墩内域水附加质量的计算较为简单，直接以桥墩内部水的质量作为附加质量，所以，空心矩形桥墩内域水的动水附加质量计算公式如式(6)所示。

min=ρwAi

(6)

式中，Ai为空心矩形桥墩内部截面积。

最终将计算的外域水和内域水的动水附加质量相加，即可得到空心矩形桥墩动水附加质量ma：

ma=mout+min=1.51(D/B)-0.17mw+ρwAi

(7)

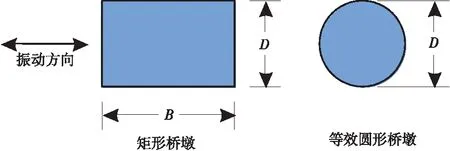
图7 矩形截面等效示意

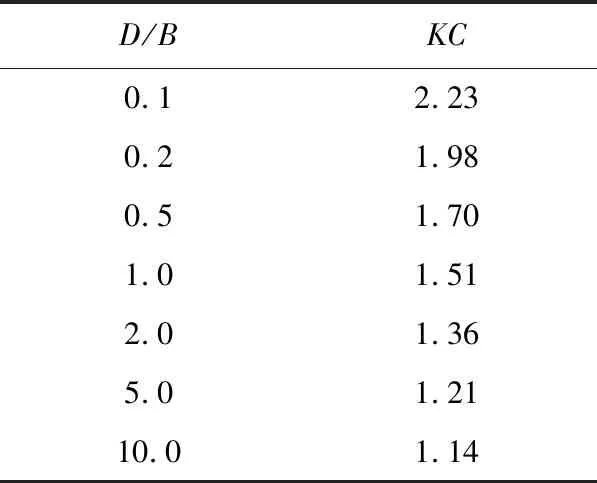
表1 附加质量修正系数KC与D/B的对应关系

3.3 附加质量模型与试验模型对比

采用USFOS软件，按欧洲规范附加质量公式，通过上述方法修正，考虑内外水域动水影响，根据水下振动台试验模型建立了相应的有限元数值模型，以及与水下振动台试验模型对比结构自振频率和地震作用下的结构响应。

3.3.1 模态对比

对于第一阶频率，附加质量模型的误差仅为2%，误差随阶数有所增加。整体而言，附加质量模型的自振频率与试验模型吻合较好(见表2)。

表2 不同模态下数值模型与试验模型对比

3.3.2 地震响应对比

在不同峰值加速度、不同地震波作用下，数值模型在各桥墩位置的加速度响应结果与试验模型整体吻合较好。El-Centro波和汶川波作用下桥墩加速度值如图8～10所示。

3.4 附加质量模型与精细化数值模型对比

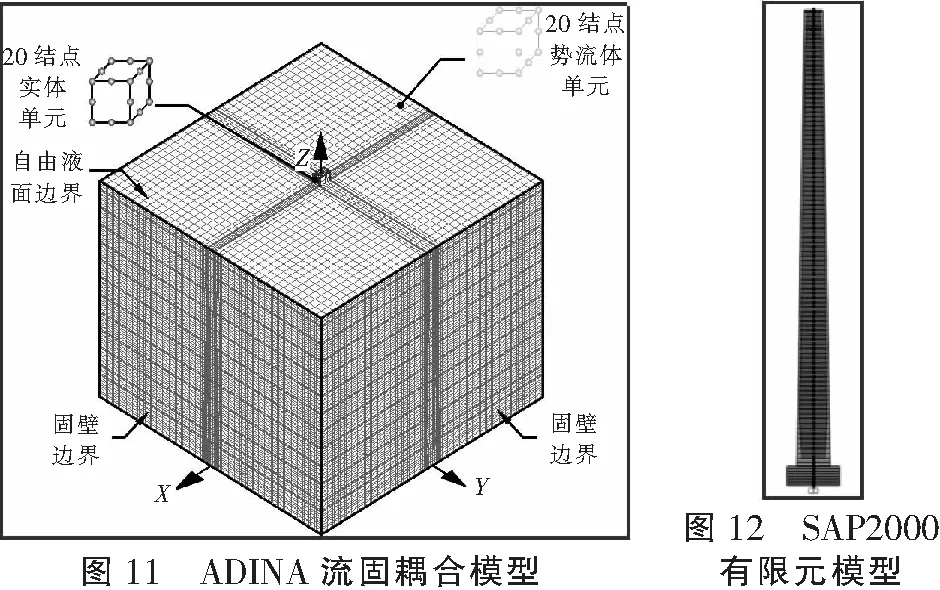
采用ADINA软件建立了基于势流体理论的精细化红旗大桥单墩流固耦合模型，见图11。采用SAP2000软件，按照欧洲规范附加质量公式，用上述方法修正，考虑内外水域动水影响，建立红旗大桥桥墩模型，见图12。

图8 El-Centro波

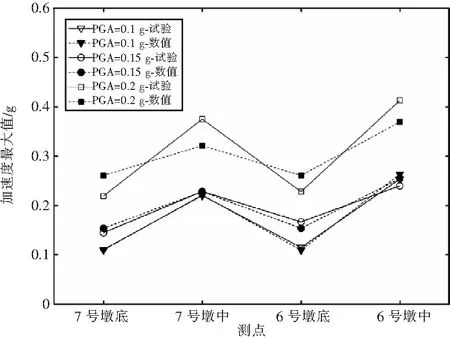
图9 汶川波

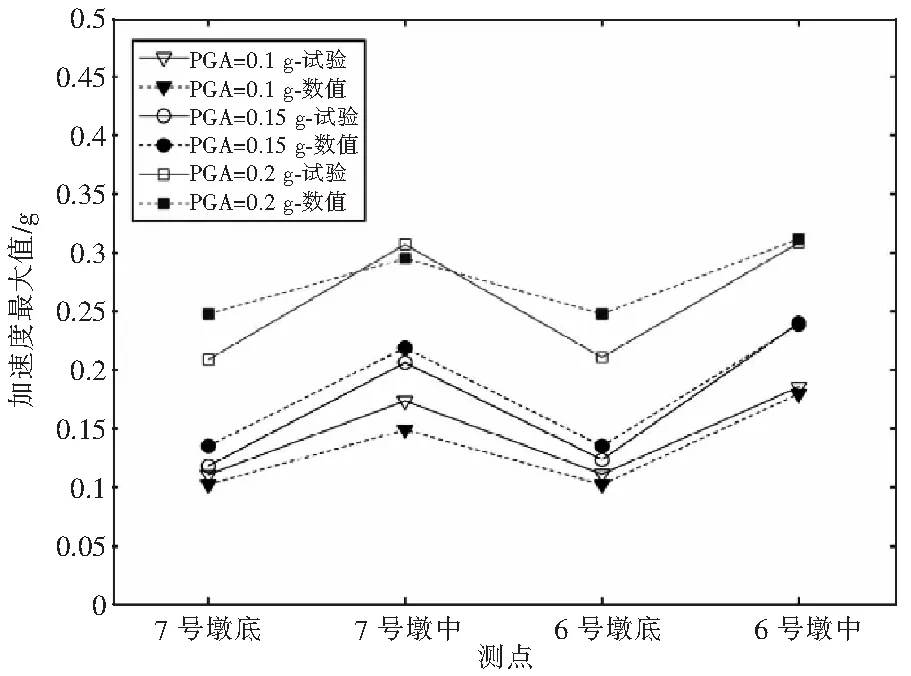
图10 人工波

通过计算，考虑汶川地震波作用下，各模型对应的桥墩弯矩及剪力峰值沿墩高分布、墩顶位移时程对比情况见图13～15。

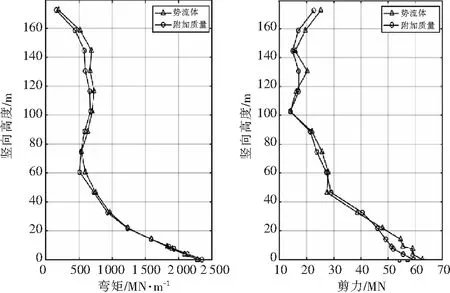
图13 弯矩最大值(汶川波) 图14 剪力最大值(汶川波)

图15 墩顶位移时程对比(汶川波)

通过对比分析，附加质量模型得到的桥墩截面弯矩响应、截面剪力响应以及墩顶位移时程等都与流固耦合模型的结果吻合良好。

综上所述，采用附加质量方法可以得到较为准确的深水桥墩截面地震弯矩、剪力响应；附加质量方法会一定程度上低估深水高墩在墩顶的地震位移响应，误差较小，均在7%左右，满足工程精度要求。鉴于附加质量方法简单、高效、精度高，在工程生产中可广泛应用。

4 结 论

本文首先通过水下振动台模型试验得到模型数据信息，再提出深水矩形空心桥墩地震动水附加质量计算方法，并采用此方法建立高效数值模型，同时建立势流体的流固耦合数值模型，对比验证了地震动水附加质量方法的准确性。通过分析得到如下结论：

(1)深水桥墩的自振频率随水深增大逐渐降低，无论是墩底还是墩顶的地震响应均随水深增大明显增加。动水效应对深水空心桥墩的结构响应影响显著，不容忽视。

(2)采用附加质量方法可以得到较为准确的深水桥墩截面地震弯矩响应、剪力响应以及墩顶地震位移响应，满足工程精度要求。

(3)分析表明，当波高、水流速较小时，波、流对于结构地震响应影响较小，不起控制作用。因此，鉴于水库地区波浪、流速均不大，在库区深水高墩桥梁地震响应分析过程中，可忽略波浪及水流作用的影响。