零耦合度部分运动解耦三平移并联机构刚度建模与分析

2020-06-29孙驰宇沈惠平王一熙许正骁袁军堂

农业机械学报 2020年6期

孙驰宇沈惠平, 王一熙许正骁袁军堂

(1.南京理工大学机械工程学院, 南京 210094； 2.常州大学现代机构学研究中心, 常州 213016)

0 引言

机构刚度是指机构动平台在外部载荷作用下，弹性构件发生形变而产生位移的度量。刚度分析对并联操作手实际应用于参数选择和结构设计都具有重要的参考价值。

目前，主要的刚度分析方法有虚拟关节分析法[1-5]、有限元分析法[6-8]以及矩阵结构分析法[9-10]。虚拟关节分析法将杆件设为刚体，在关节处通过建立柔性关节来描述杆件和关节所累积的柔性量；有限元分析法对杆件和关节的建模都需建立准确的物理模型，因此精度高，但其计算量较大；矩阵结构分析法将杆件和关节看作单元，相比于其他两种方法，其分析效率高，但无法直接得到笛卡尔系的刚度矩阵。

基于以上3种刚度分析方法，国内外学者进行了诸多刚度建模实例分析。胡波等[11]给出了考虑约束反力产生变形的刚度建模方法，基于虚功原理建立机构静力学方程，通过分析机构在合力作用下的变形量给出机构刚度；徐东涛等[12]基于传统的机构刚度映射矩阵建立机构刚度模型，并提出以机构弹性变形评价机构刚性特性的方法；曲海波等[13]通过锁定机构驱动副，运用互易积运算求解动平台反螺旋力系，再以此推导出机构刚度及动平台的广义位移；周玉林等[14]基于机构各构件的弹性变形，利用小变形叠加原理导出机构静力学方程，再运用正交变换得到机构静刚度；杨超等[15]运用螺旋理论和应变能方法研究了具有2R1T三自由度的2UPR-RPU过约束并联机构的静弹性刚度性能，模型考虑了杆件和关节的柔度；CECCARELLI等[16]研究了力的传递及力作用下的机构变形，以此推导出机构的刚度矩阵；MAJOU等[3]通过参数化刚度分析建立了正交矩阵的相容模型，在各向同性结构中计算刚度矩阵元素，从而得到机构刚度；PASHKEVICH等[17]提出利用6自由度虚拟弹簧建立刚度模型的方法；YAN等[18]基于Castigliano第2定理，利用应变能法推导出一般平行四边形机构刚度的代数表达式，得到机构的整体刚度矩阵。

虚拟弹簧法基于虚拟关节分析法，是一种通过在弹性连杆的末端增加虚拟弹簧来描述连杆的线性/旋转变形以及变形之间的耦合特性的建模方法[19-20]，可对并联机构的支链进行单独建模，相比于上述建模方法，该方法不需要推导各类复杂的雅可比矩阵或运动映射关系，仅需利用机构的运动学逆解即可计算机构刚度(含处于奇异位形时)。

三平移并联操作手在定位、抓取、装卸等各种产业工艺操作上具有较广泛的应用。笔者团队提出一种新型零耦合度的非对称三平移并联操作手，该机构可得到位置正解的解析解，同时，还具有运动部分解耦特性，其运动控制及轨迹规划较易，已完成其运动学分析和计算[21]。本文基于虚拟弹簧法对此机构进行刚度建模与特性分析，给出机构整体刚度在工作空间中的分布规律，以及该机构在不同方向、不同高度截面上的扭转、线性刚度特性，以期为该操作手的动力学分析、样机设计及其实验研究提供理论基础。

1 机构描述

(RPa∥3R)2R+RPa三平移并联机构的拓扑结构如图1所示，它由动平台1、静平台0及2条混合支链(HSOC)组成，坐标系如图1所示[22]。

图1 零耦合度且运动解耦的非对称三平移并联机构Fig.1 Asymmetric three-translational parallel mechanism with zero coupling degree and motion decoupling

混合支链Ⅰ由支链A、B、C组成，其中4个球副(Sa、Sb、Sc、Sd)组成的平行四边形结构(Pa(4S))，支链A由驱动副R11串联Pa(4S)组成；R11轴线与平行四边形SaSb边平行；支链B为驱动副R21串联R22与R23组成，它们轴线相互平行；支链C由R12串联R13组成，它们轴线相互平行。因此，混合支链Ⅰ记为：(RPa(4S)3R)⊥2R。混合支链Ⅱ为驱动副R31串联R32后，又串联由4个R副(Re、Rf、Rg、Rh)组成的平行四边形结构(Pa(4R))，进一步再串联R33组成，R31、R32、R33的轴线相互平行，因子串ReR32Rf、RgR33Rh分别等效于2个球副(S)，因此，该平行四边形相当于4个球副组成的平行四边形，但不存在绕其对角线的转动，故混合支链Ⅱ可记为：RPa。

该机构自由度为3，当取静平台0上的3个转动副R11、R21、R31为驱动副时，动平台1可实现沿x、y、z轴的三维平移，且沿y、z轴向的位移仅由驱动副R11、R21确定，因而具有输入-输出部分运动解耦性[23]。

2 刚度模型建立

2.1 单杆刚度矩阵

建立刚度模型时，可将单杆看作悬臂梁，通过分析其末端变形求解刚度矩阵。在单杆受到力/力矩作用时，根据欧拉-伯努利梁理论，可得连杆的挠曲线方程，在弯曲变形很小且材料服从胡克定律的情况下，挠曲线方程是线性的，因此，考虑到连杆受力/力矩的耦合情况，采用叠加法计算连杆在力/力矩作用下的柔度矩阵，再对柔度矩阵求逆，即可得到单杆刚度矩阵为[20，25]

(1)

式中G——杨氏模量

Ix、Iy、Iz——截面关于x、y、z轴的惯性矩

l——单杆杆长

E——弹性模量

A——杆件截面积

式(1)是计算机构各支链及整体刚度矩阵的基础。为便于后续表述和计算，将式中各元素的表达式分别记作Kij。

2.2 4S平行四边形结构刚度矩阵

平行四边形结构无法直接采用单杆的刚度矩阵进行计算，需要将其作为独立结构进行刚度建模。在4S平行四边形结构中，建立图2所示的局部坐标系，其中，平行四边形的两短杆可视为刚性构件，两长杆可视为悬臂梁。o1点为四边形结构末端基点；x1轴方向与两短杆中点连线重合，指向o1点；y1轴方向垂直于四边形平面向外，z1轴方向由右手法则确定。

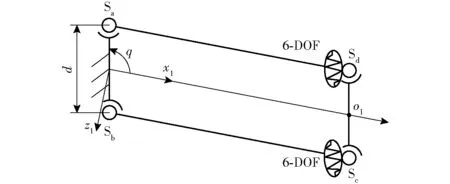
图2 4S平行四边形结构的刚度模型Fig.2 Stiffness model of 4S parallelogram structures

4S四边形结构的刚度矩阵为

(2)

其中，Sq表示sinq，下同。

2.3 4R平行四边形结构刚度矩阵

对于4R平行四边形结构，局部坐标系建立方法同图2，如图3所示，平行四边形的两短杆可视为刚性构件，两长杆可视为悬臂梁。

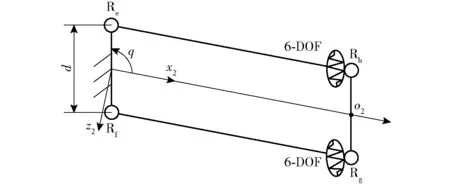
图3 4R平行四边形结构的刚度模型Fig.3 Stiffness model of 4R parallelogram structures

因此，4R四边形结构的刚度矩阵为

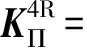
(3)

其中，Cq表示cosq。

因末端点o2沿z2方向的力受到被动副Re、Rf与被动副Rh、Rg的补偿而消失，因此，该4R四边形结构的末端可用5-DOF的虚拟弹簧来描述其刚度特性。

2.4 一般支链的刚度建模

2.4.1运动方程的建立

一般支链通常由驱动副(Ac)、主动杆、从动杆以及被动副组成，其虚拟弹簧模型如图4所示。

图4 4R一般支链的虚拟弹簧模型Fig.4 Virtual spring model of 4R branch chain

1-DOF的虚拟弹簧，表示驱动副Ac的伺服刚度，其变形可表示为Δθ0；6-DOF的虚拟弹簧，表示杆件在笛卡尔坐标系中三自由度的旋转变形和三自由度的拉伸变形，主动杆和被动杆上弹簧的变形量可分别表示为(Δθ1,Δθ2,…,Δθ6)和(Δθ7,Δθ8,…,Δθ12)。

基于图4给出支链中弹簧变形和被动关节变形到末端变形之间的一般性运动方程为

(4)

其中

式中 Δt——静笛卡尔坐标系中机构末端变形

Δφ——旋转变形 Δp——拉伸变形

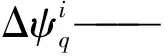
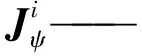
将式(4)的支链运动方程表示成螺旋运动形式，即

(5)

其中

式中 $——机构末端参考点变形的旋量

Δθi——虚拟弹簧变形量

Δψi——被动副运动位移

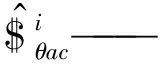
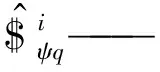
2.4.2静力学方程的建立

(6)

因此，外力fi所做虚功为

(7)

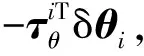
(8)

而被动关节受力后会发生被动运动，所以在静平衡状态下，被动运动不做功，即

(9)

由式(8)、(9)可得

(10)

(11)

于是，支链的静力平衡方程可表示为

(12)

其中

令支链i的笛卡尔刚度矩阵为Ki，则有

fi=KiΔt

(13)

式中fi——支链i所受的外力

由式(12)、(13)可得

(14)

由于每条支链所受外力为机构整体所受外力的分量，因此，一般整体的刚度矩阵为

(15)

2.5 机构的刚度建模

该三平移并联机构由2条HSOC构成，其支链拓扑结构简化后如图5所示。

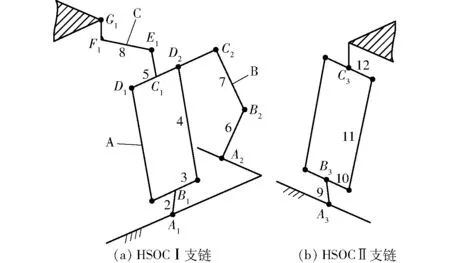
图5 机构的支链拓扑结构简图Fig.5 Schematics of branch chain

2.5.1HSOCⅠ的刚度建模

HSOCⅠ由支链A、B并联组成子并联机构后再串联支链C组成，因此，先分别求出支链A、B的刚度矩阵，即可求得子并联机构的刚度矩阵；再将它看成一个整体与支链C串联进行刚度建模，即可得到HSOCⅠ的刚度矩阵。

(1)支链A的刚度矩阵

支链A的刚度模型如图6所示，其中，驱动副(Ac)对应笛卡尔坐标系中1个旋转自由度的虚拟弹簧变形；主动杆杆2对应笛卡尔坐标系中6个自由度的虚拟弹簧变形，包含3个旋转变形和3个线性变形；4S平行四边形结构对应笛卡尔坐标系中2个自由度的虚拟弹簧(2.2节)。在支链A中，所有被动副均在4S平行四边形结构内，可将其看成整体结构，因此，可认为支链A不包含被动副。

图6 支链A的虚拟弹簧模型Fig.6 Virtual spring model of branch chain A

由式(12)、(14)可得支链A的静力方程为

其中

式中KA——支链A的刚度矩阵

KAc——驱动刚度

(2)支链B的刚度矩阵

支链B的刚度模型如图7所示，其中，驱动副(Ac)对应笛卡尔坐标系中1个旋转自由度的虚拟弹簧变形；主动杆杆6和从动杆杆7各对应笛卡尔坐标系中6个自由度的虚拟弹簧变形。

图7 支链B的虚拟弹簧建模型Fig.7 Virtual spring model of branch chain B

由式(12)、(14)可得支链B的静力方程为

其中

eB=[0 -1 0]T

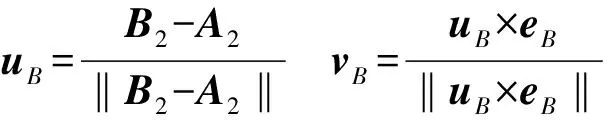
式中KB——支链B刚度矩阵

在求得支链A和B的刚度矩阵后，由式(15)可得子并联结构的整体刚度矩阵为

Ksub=KA+KB

(3)混合支链的刚度矩阵

将支链A、B组成的子并联机构看成一个整体与支链C串联进行刚度建模，混合支链的刚度模型如图8所示，其中，从动杆杆8对应笛卡尔坐标系中6个自由度的虚拟弹簧变形；杆C1E1、F1G1因杆长远短于其他杆件，因此，将它们看作刚性构件，不考虑在其末端建立虚拟弹簧。

图8 HSOCⅠ的虚拟弹簧模型Fig.8 Virtual spring modeling of HSOC Ⅰ

由式(12)、(14)可得HSOCⅠ的静力方程为

其中

e1=[1 0 0]Te2=[0 1 0]T

e3=[0 0 1]T

式中K1——混合支链Ⅰ的刚度矩阵

2.5.2HSOCⅡ的刚度建模

HSOCⅡ的刚度模型如图9所示，其中，驱动副(Ac)对应笛卡尔坐标系中1个旋转自由度的虚拟弹簧变形；主动杆杆6对应笛卡尔坐标系中6个自由度的虚拟弹簧变形；4R平行四边形结构对应笛卡尔坐标系中5个自由度的虚拟弹簧(由2.3节说明)。被动副R32、R33各存在1个自由度的微小变形。

图9 HSOCⅡ的虚拟弹簧建模Fig.9 Virtual spring modeling of HSOCⅡ

由式(12)、(14)可得HSOCⅡ的静力方程为

其中

式中K2——混合支链Ⅱ的刚度矩阵

由式(15)可得机构的整体刚度为

K=K1+K2

3 刚度分析

3.1 机构参数

机构各杆件的尺寸参数如表1所示。为了减轻机构质量，提高机构强度，机构杆件全部选择碳纤维材料。机构3个驱动输入采用相同的驱动电机，其驱动刚度取为5×104N·m/rad。

表1 机构杆件尺寸参数Tab.1 Dimension parameters of mechanism

3.2 数值算例

根据第2节中的刚度矩阵建模，可计算出机构在某一姿态下的整体静刚度矩阵。现取动平台基点p的坐标为(0.02,0.03,0.8)，可得该姿态下机构的整体刚度为

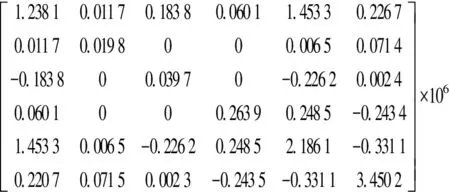
(16)

可知刚度矩阵K为6×6方阵，其中，对角线前3项为机构在x、y、z轴方向的扭转刚度(单位：N·m/rad)；后3项为机构在x、y、z轴方向的线性刚度(单位：N/m)。

机构在运动过程中，刚度随着机构末端基点位置的变化而变化，为研究其分布规律，定义刚度矩阵中对角线上6项数值的平均值η[24]，即

(17)

利用Matlab软件计算η在机构工作空间中的分布，如图10所示。

由图10可知，当动平台在y轴方向上越靠近两侧时，机构的整体刚度越大；为更加清晰地分析z轴方向对机构整体刚度的影响，利用Matlab软件计算机构工作空间中z=0.75 m和z=0.90 m两截面的η分布，如图11所示。

图10 工作空间中机构的刚度分布Fig.10 Stiffness distribution of mechanism

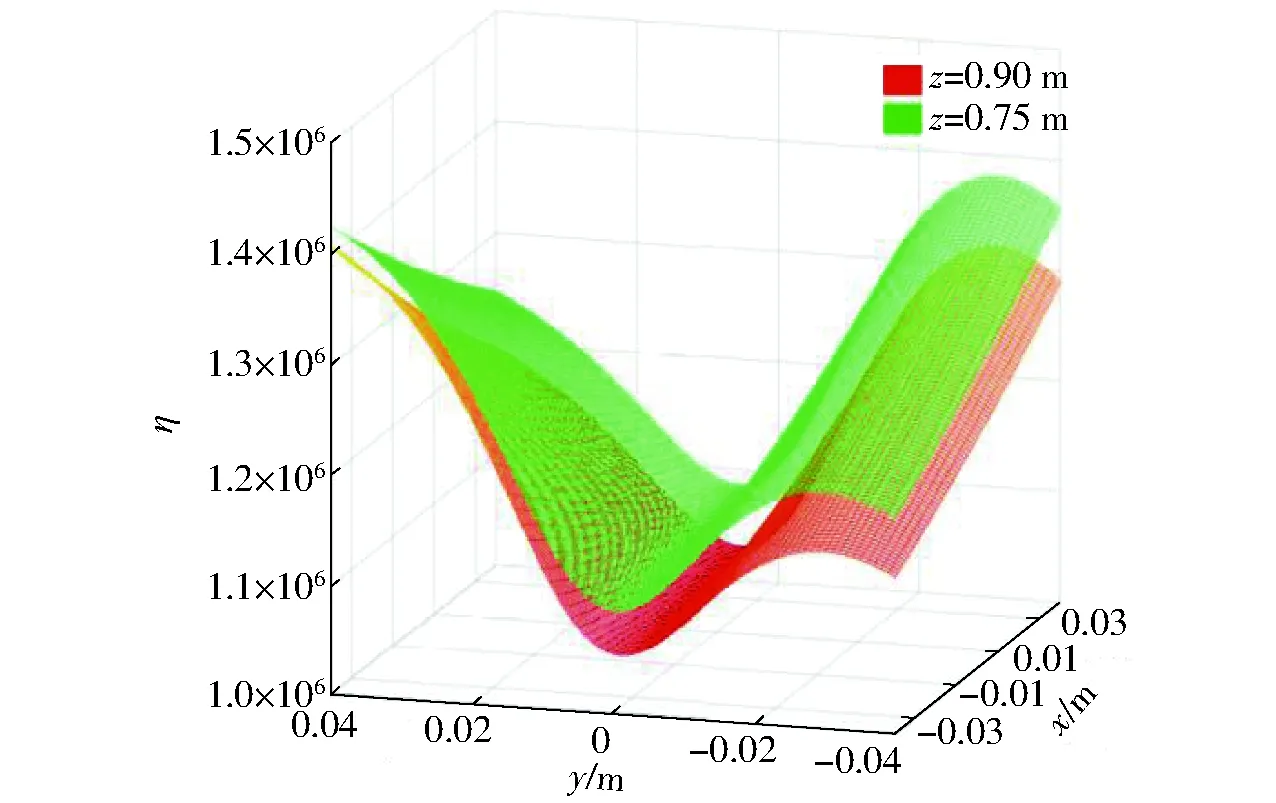
图11 不同z值截面的机构刚度分布Fig.11 Stiffness distribution of mechanism with different z sections

由图11可知，动平台在不同高度下，刚度变化趋势相似；但随着z的减小，机构整体刚度变大。

为了更加具体地分析刚度矩阵中各方向的扭转刚度和线性刚度的分布情况，取机构工作空间中z=0.75 m和z=0.90 m两截面进行分析，如图12所示。

图12 不同z值截面的刚度矩阵主对角线元素分布情况Fig.12 Distributions of main diagonal elements of stiffness matrix with different z-sections

由图12可知，机构x轴方向的扭转刚度最大，y、z轴方向的扭转刚度相近，原因为支链B不能绕x轴方向旋转，因此，x轴方向的扭转刚度高于其他两轴方向。z轴方向的线性刚度最大，原因为该类机械手在工作时，其所受的外部线性载荷主要由z轴方向承担，因此，需要z轴方向有较大的线性刚度。刚度特性均随着z的减小而增大，说明机构动平台离定平台越近，刚度越大，因此，只要机械手在刚抓取物件时不发生变形，则在其向上提升物件的运送过程中，机构也不会变形，这一特性符合机械臂的抓取性能需要。

3.3 数值验证

为了验证数值算例的正确性，现将该机构的简化模型导入ANSYS Workbench，进行有限元分析(FEA)。当机构末端基点p的位置坐标为(0.02,0.03,0.8) m时，在动平台上施加单位力、力矩，将动平台看作刚性无限大的柔性构件，对机构进行刚柔耦合分析，网格划分如图13a所示；考虑约束和受力，如图13b所示。由此得到动平台相对于静坐标系各个方向产生的微小位姿变化，其值分别对应虚拟弹簧法(VSM)中所得刚度矩阵的逆矩阵中对角线上6个元素的数值。

对式(16)求逆，可得机构的柔度矩阵为

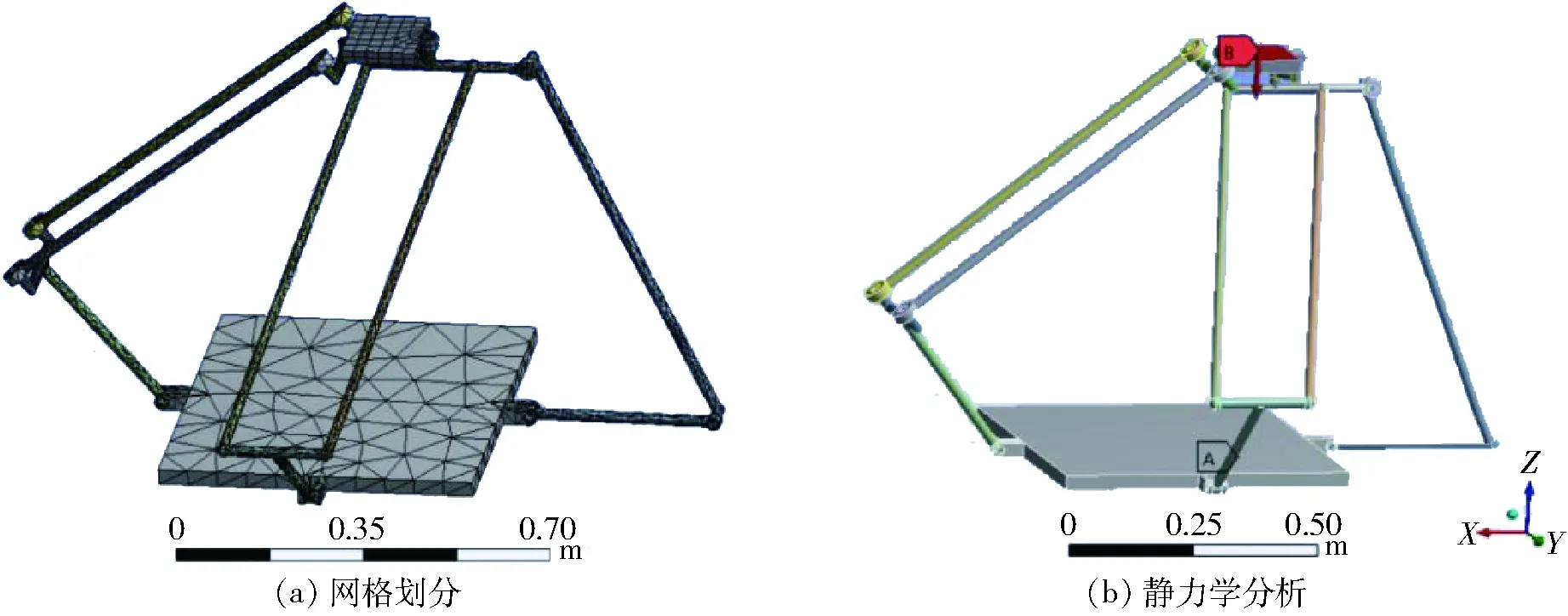
图13 机构的刚柔耦合分析Fig.13 Rigid-flexible coupling analysis of mechanism

将有限元分析所得的机构变形结果与虚拟弹簧法所得的机构变形结果进行对比，并得到其相对误差，如表2所示。

由表2可知，理论变形与仿真变形的误差在-6%内。因此，虚拟弹簧法的建模精度满足工程设计要求。

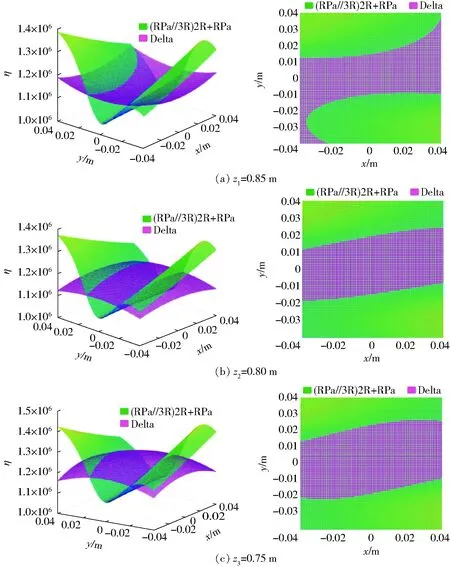
图14 两机构的η值分布Fig.14 η distributions of two mechanisms

4 (RPa∥3R)2R+RPa与Delta机构的刚度比较

将三平移(RPa∥3R)2R+RPa机构与Delta机构进行刚度比较，两者选取相同的机构参数(3.1节)，取工作空间中z1=0.85 m、z2=0.80 m、z3=0.75 m处的3个截面进行研究。

根据文献[25]中Delta机构的运动学反解，使用Matlab编程，得到3个截面中两机构的刚度参数η在x∈[-0.04,0.04] m，y∈[-0.04,0.04] m范围内的分布，及其在xoy平面的投影，如图14所示。

由图14可知，(RPa∥3R)2R+RPa机构与Delta机构，在y轴方向上越靠近两侧时，机构的整体刚度越大。Delta机构的刚度分布曲面更为规则且刚度变化更为平稳。(RPa∥3R)2R+RPa机构的刚度大于Delta机构的部分在z1、z2、z3截面中所占的面积(图中绿色部分)分别为60.54%、58.69%、56.37%(由划分网格的面积估算)，均大于50%，因此，可得(RPa∥3R)2R+RPa机构的刚度较大于Delta机构。