高流量呼吸湿化治疗仪的机理分析与数据建模
2020-06-29魏立峰1私1李雨桐1周成广孙明仪
魏立峰1,杨 私1,李雨桐1,周成广,孙明仪
(1.沈阳化工大学 信息工程学院,沈阳 110021; 2.沈阳迈思医疗科技有限公司,沈阳 110021)
0 引言
近年来,随着呼吸医学研究深入和工程技术的不断发展,针对呼吸衰竭疾病的治疗方法不断改善与提高。由各种原因引起的肺通气和换气功能严重障碍,以至在静息状态下亦不能维持足够的气体交换,导致低氧血症伴高碳酸血症,进而引起一系列病理生理改变和相应临床表现的综合症。由于呼吸衰竭导致的低氧血症;是一种呼吸衰竭引起的通气障碍导致血氧低于正常值,长期处于低血氧状态会损害全身各重要脏器的功能,并诱发和加重一系列的病情,严重者发生猝死或神经系统疾病,这种伤害是不可以逆的,对身体的危害极大。因此,临床上对于低氧血症的快速纠正是保护患者生命健康和治疗急慢性呼吸衰竭的一个重要手段。
高流量呼吸湿化治疗仪(HiFent)是一种新型呼吸支持技术[1-3],能够快速纠正低血氧症,可以给患者提供具有氧浓度、温度和湿度相对恒定的高流量气体。因为HiFent提供31~37℃且湿度为90%左右的气体,所以它具有良好的舒适性。HiFent可以给予高于患者自身吸气峰流量的气体,此时就可以确定患者实际的吸氧浓度和流量并保持稳定。高流量气体可以冲刷咽部的死腔,减少CO2的重复吸入,高湿气体可以改善气道黏膜纤毛运动有利于分泌物的排除减少肺不张的形成。
湿度的控制精度是HiFent保证治疗效果的关键。高流量气体的湿度过高会导致加热管路中形成冷凝水,进而引起HiFent使用舒适度下降,甚至引发医疗事故。而湿度过低达不到理想的治疗效果。在实际的应用中,如果选取湿度为控制对象,湿敏元件的响应时间、湿滞回线和温度系数会影响湿度测量值的稳定性导致控制系统可靠性下降,所以选取温度为控制对象,通过控制温度来间接控制湿度。建立准确可靠的HiFent系统稳态模型,并结合经典的控制方法可以对湿度间接控制提供有效的指导。目前,HiFent湿度间接控制仅仅为简单的分区位式控制,受限于控制方式的局限性,导致湿度在区间内波动。本文分析了HiFent的系统结构和工作原理,通过HiFent热传递方式来构建机理模型[4-5],建立了适用于HiFent稳态过程的绝对湿度控制模型,并进行了实验验证。
1 高流量呼吸湿化治疗仪的机理建模分析
HiFent的示意图如图1所示,空氧混合气体首先通过风机送入湿化罐,然后加热片对湿化罐进行加热,产生高温高湿的混合气体,再通过加热管路的加温后进入鼻塞导管,最后混合气体自然冷却后送入人体内。可将HiFent的工作过程分为四个部分:风机输送气体、湿化罐对气体加温加湿、加热管路对气体加温和鼻塞导管中气体的自然冷却过程。其中,湿化罐出气口温度控制为关键所在,它决定后续气体的湿度,直接影响湿化仪的治疗效果。
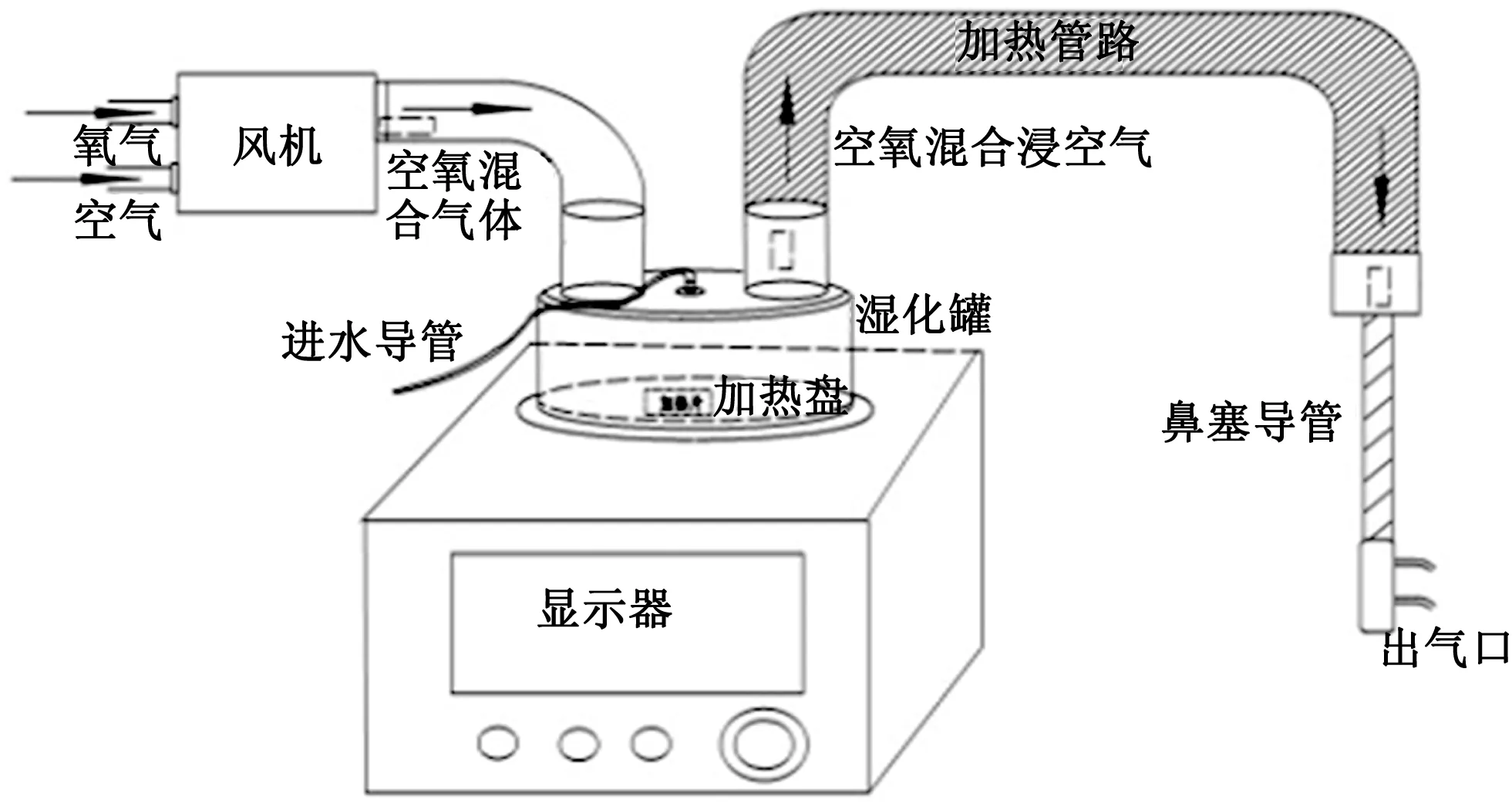
图1 高流量呼吸湿化治疗仪示意图
1.1 湿化罐传热模型分析
湿化罐出气口绝对湿度受加热片的散热影响。散热存在三种形式:传导散热、对流散热和热辐射散热。传导散热是指热量在系统内部或系统之间传递的现象,是固体的主要散热方。对流散热是气体或液体通过自然流动或者强迫流动散热的现象,是液体和气体的主要散热方式。热辐射散热是指高温物体以辐射的方式向外辐射散热的现象,一般通过电磁辐射的方式散热,且温度越高辐射的能量越大,在实际生活中,大多数的散热过程都是三者组合而成的复合散热过程。由能量守恒可知:加热片发热量=湿化罐出气口热量+湿化罐热损失-湿化罐进气口热量。如图2所示,热量的输入为湿化罐进气热量和加热片发热量的总和,热量的输出为湿化罐出气口热量和湿化罐与环境之间的热交换的总和。
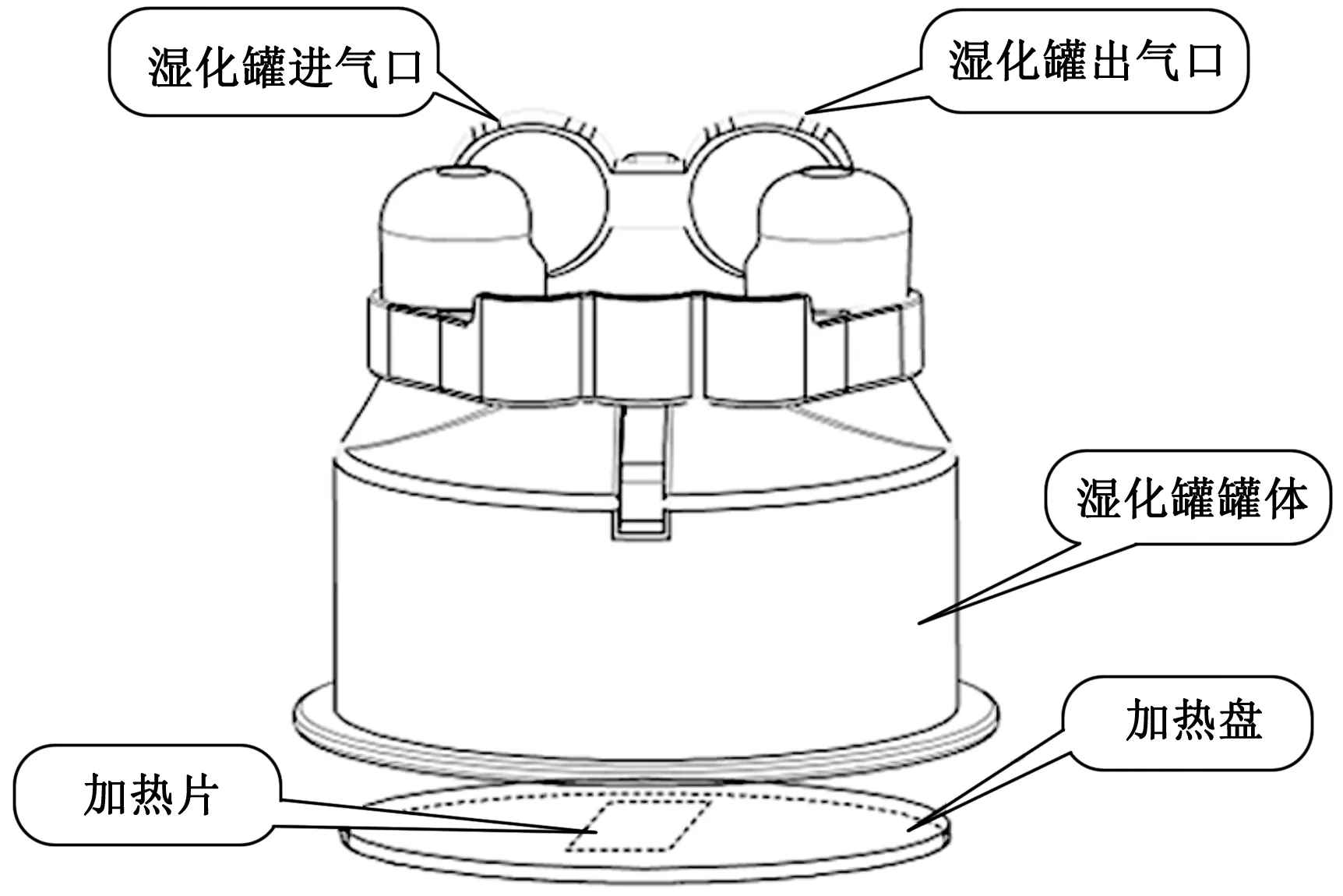
图2 湿化罐加热结构示意图
由能量守恒定律可知:
Qi=Qs1+Qs2-Qs3
(1)
式中,Qi为加热片发热量(J);Qs1为湿化罐出气口气体热量(J);Qs2为湿化罐热损失(J);Qs3为湿化罐进气口气体热量,J。
1)加热片的热量计算公式为:
(2)
式中,U为加热片两端的电压值(V);R为加热片的电阻值(Ω)。
2)湿化罐出气口气体热量计算公式为:
Qs1=mgcv,gtg
(3)
式中,mg为出气口某一段时间内气体的质量(kg);cv,g为出气口气体恒容比热容(J/kg·℃);tg为出气口气体的温度(℃)。
3)热损失计算公式:
湿化罐的热损失可以分为三类:热传导、热对流和热辐射[6-7]。
湿化罐壁的热传导散热,由傅立叶导热定律[3]建立导热表达式:
(4)
式中,γ为罐壁的导热系数;ti为湿化罐內水温(℃);te为湿化罐的环境温度(℃)。
导热系数与物体的种类、结构、密度、温度和成分等很多因素有关,但是温度的影响为更为显著,各种物质的导热系数均随温度变化而变化。在一定的温度范围,大多数材料的导热系数可以作为温度的线性函数。
γ=1+ati
(5)
由式(4)和式(5)可知:
Qs=(1+ati)(ti-te)
(6)
湿化罐对流散热,由牛顿对流冷却定律建立对流换热表达式:
Qc=hmS(ti-te)
(7)
式中,hm为对流换热系数;S为湿化罐的表面积(m2);ti湿化罐內水温(℃);te为湿化罐的环境温度(℃)。
本文的对象为湿化罐可以视为大空间自然对流换热,这种类型的自然对流换热处理与流体性质、和环境温度有关,还会受空间位置、形状、尺寸比例等影响。传统的自然对流关联式可表示为:
(8)
式中,g为重力常数(N/kg);α为体积膨胀系数,对空气假设α=1/te;l为特征长度;ρ为湿化罐內空气密度(kg/m3);v为湿化罐內空气动力粘度系数;cp为湿化罐內空气比热容,φ为湿化罐內空气导热系数。
根据上式可以得到湿化罐的对流换热表达式为:
(9)
湿化罐辐射散热,物体的辐射能力与温度遵守四次方定律,湿化罐的辐射能力与绝对温度的关系可以表示为:
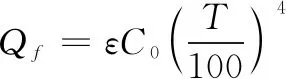
(10)
式中,ε为湿化罐的黑度,C0为黑体的辐射系数,5.675 W/m2·K4;T为湿化罐的绝对温度(K)。
由上可知热损失的计算式为:
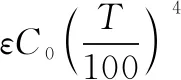
(11)
4)湿化罐进气口气体热量计算公式:
Qs3=mccv,c)tc
(12)
式中,mc为进气口某一段时间内气体的质量(kg);cv,c为进气口气体恒容比热容(J/kg·℃);tc为进气口气体的温度(℃)。
综上所述可知湿化罐的传热模型为:
(13)
通过对高流量呼吸湿化治疗仪的湿化罐传热机理进行分析,建立了湿化罐传热模型。式(13)中当系统达到稳态时,加热片电压与湿化罐出气口气体比热容的关系,温度稳定时气体比热容和绝对湿度存在线性关系。但是加热片电压还受环境温度、湿化罐体的材质、形状、大小的影响。由分析模型可知,湿化罐传热过程复杂,模型具有多元、高阶次和非线性,且涉及的热力学参数多,模型比较复杂。此外,湿化罐散热受环境影响较大,容易对控制形成干扰,在设计控制器时需要考虑外界干扰作用并进行补偿。
2 高流量呼吸湿化治疗仪的数据建模
在实际的工程应用中,气体的绝对湿度无法在线实时测量,热量传导具有较大滞后性,难以实现绝对湿度的实时控制。但气体的比热容和气体的绝对湿度有线性关系,由湿化罐的传热模型可知,气体的热量与比热容是近似线性关系,即气体绝对湿度与热量存在近似线性关系。所以本文采用间接控制方法,通过对易于测量与控制的气体温度来实现控制绝对湿度的目的。
在对湿化罐的机理建模中,在现有的设备和可辨识参数的基础上,采用多元线性回归建模的方法,提供一个简单实用的数学模型。选取湿化罐进气口的温度、湿化罐进气口的相对湿度、流量和湿化罐出气口绝对湿度这4个变量为模型的输入,湿化罐出气口的温度作为模型的输出,通过医疗仪器产品质量分布式检测系统来采集输入输出变量的数据信息。
2.1 稳态检测
检测系统后台数据包中,包含动态过程和在受到干扰时的大量非稳态运行数据[7-8]。在动态过程中,因为采用的是离心式风机,气体进入时会环绕电机一圈对电机进行降温,而电机的发热是一个缓慢的过程,所以湿化罐进气口的温湿度会受到影响且时间较长。以75 L/min实验数据为例,采样时间为1 s,湿化罐进气口温湿度随时间变化的趋势如图3所示。
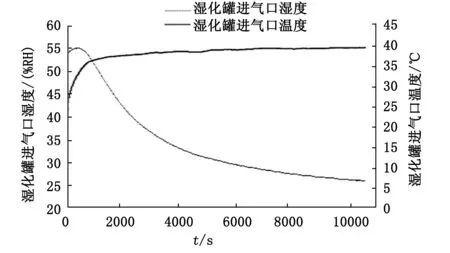
图3 湿化罐温湿度随时间变化的趋势
湿化罐温湿度的初始值分别为23.4℃和53.6%RH,因为风机散热影响使得湿化罐进气口的温湿度在9000 s后才能稳定。在此之前的数据不能真实地反应系统输入、输出之间的关系,会影响建模的精度。所以需要进行稳态检测,在稳定的工况下提取运行数据,之后对稳态时间内的数据取平均值,此时的数据才能真实反映各变量之间的关系。
2.2 多元线性回归数据建模
多元线性回归模型[9-10]研究的是因变量与多个自变量的变化关系,但是又有许多不可预测的随机因素影响它们之间的关系,无法从理论的角度去表示它们的关系,只能通过数理统计的方法解释他们存在的数理关系。在复杂的条件或是工况下,输出结果会被多个输入影响,因此需要对单个输出变量和多个输入变量联系起来进行分析[11-12]。例如在湿化仪的控制过程中,湿化罐出气口温度受到环境温湿度、风机散热和流量等多个变量的影响。采用多元线性回归的方法,把函数曲线逼近实验数据得到的模型为:
Y=β0+β1X1+β2X2+β3X3+β4X4+ε
(14)
Y为湿化罐出气口温度;X1为流量;X2为湿化罐进气口温度;X3为湿化罐进气口相对湿度;X4为湿化罐出气口绝对湿度;ε为随机误差;β0,β1,β2,β3,β4为回归系数。
在稳态的条件下,通过调节湿化罐出气口温度值,使得湿化罐出气口的绝对湿度值大约为40 mg/L,统计各个变量的平均值如表1所示。
由表1可知,因为湿化罐进气口温度、湿化罐进气口相对湿度和湿化罐出气口绝对湿度与湿化罐出气口温度之间有较强的线性关系,所以使用多元线性回归模型来分析和拟合各个变量之间的关系。用Matlab中的regress函数拟合得到最后的模型为:
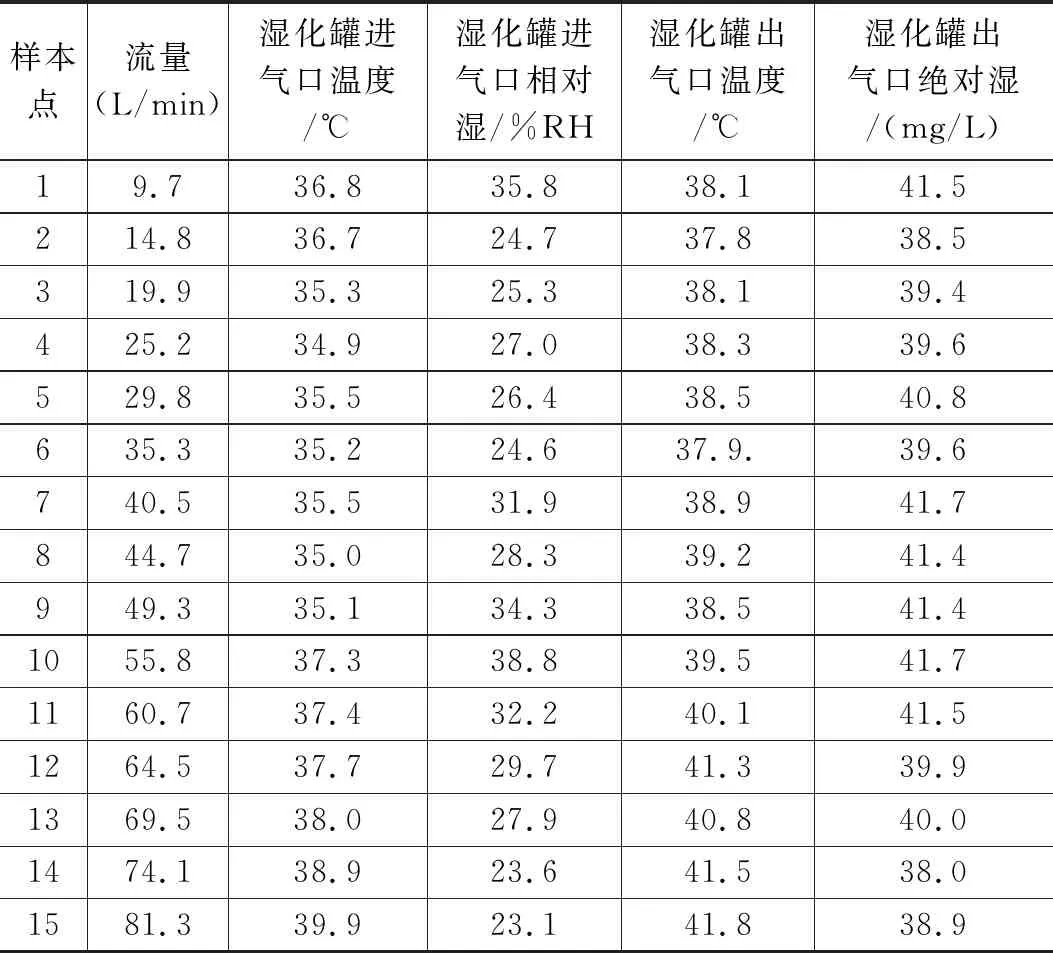
表1 稳态时各个变量的平均值统计表
Y=19.3359+0.0394X1+0.3952X2-
0.0551X3+0.1335X4
(15)
模型拟合数据与实测数据的对比如图4所示。
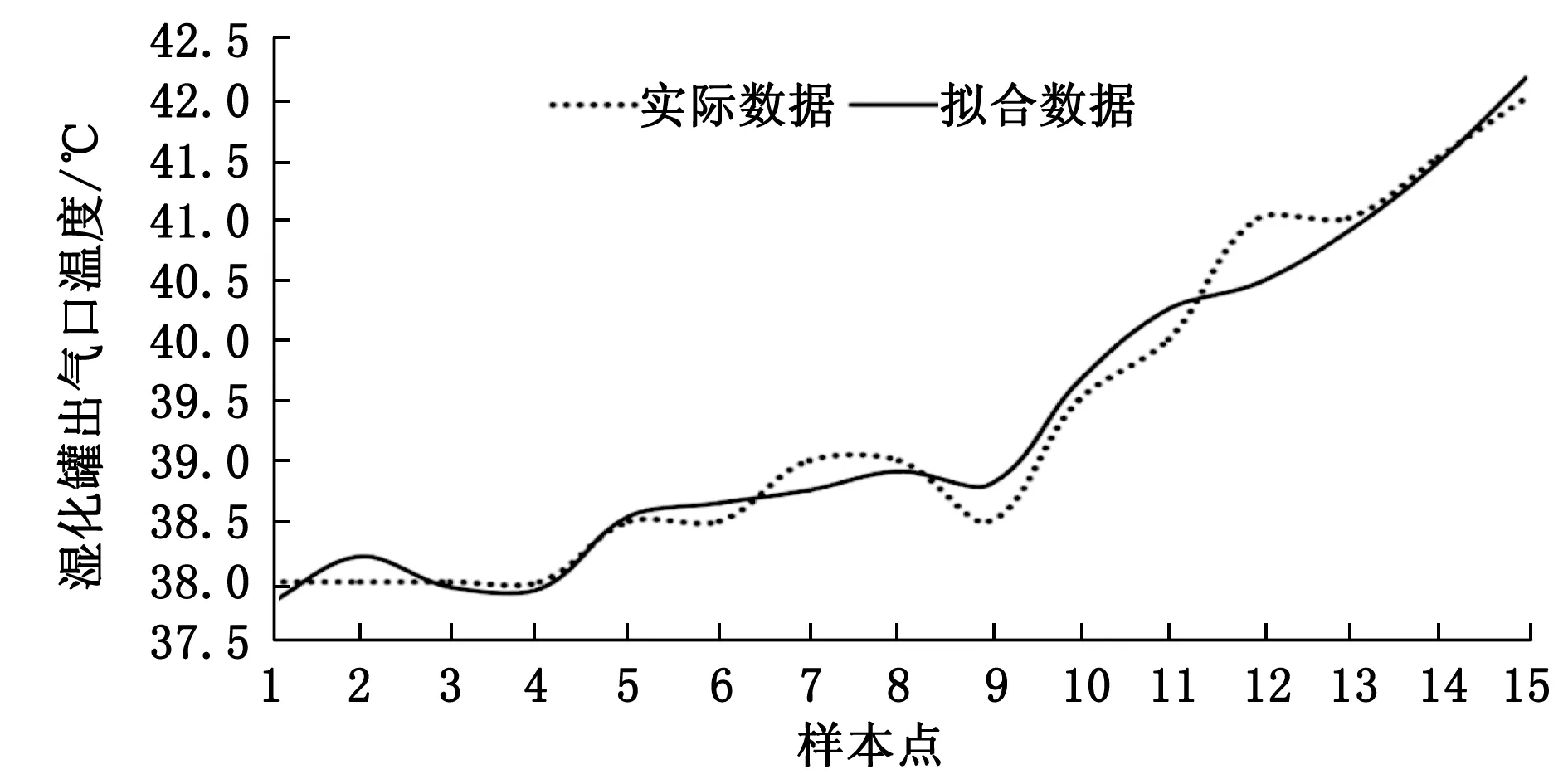
图4 湿化罐出气口温度拟合曲线与实际曲线
2.3 多元线性回归与实验数据检验
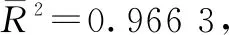
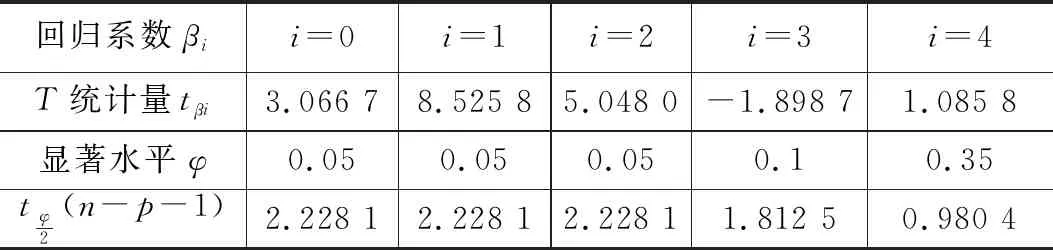
表2 回归参数的T统计量
通过以上检验得出,回归方程的总体回归性显著,但是湿化罐出气口绝对湿度的显著水平相对较低。因为湿化罐加湿过程是水蒸发过程,加湿气体温度和绝对湿度的关系与气压、气体比热和流量等因素有关。
实验数据检验,流量从10~80 L/min每隔5 L/min一组,绝对湿度期望值为40 mg/L。当湿化罐进气口温湿度稳定时,依据稳态回归模型求得湿化罐出气口温度目标给定值。通过对湿化罐出气口温度反馈控制,实现对湿化罐出气口绝对湿度的间接控制。实验数据如表3所示。
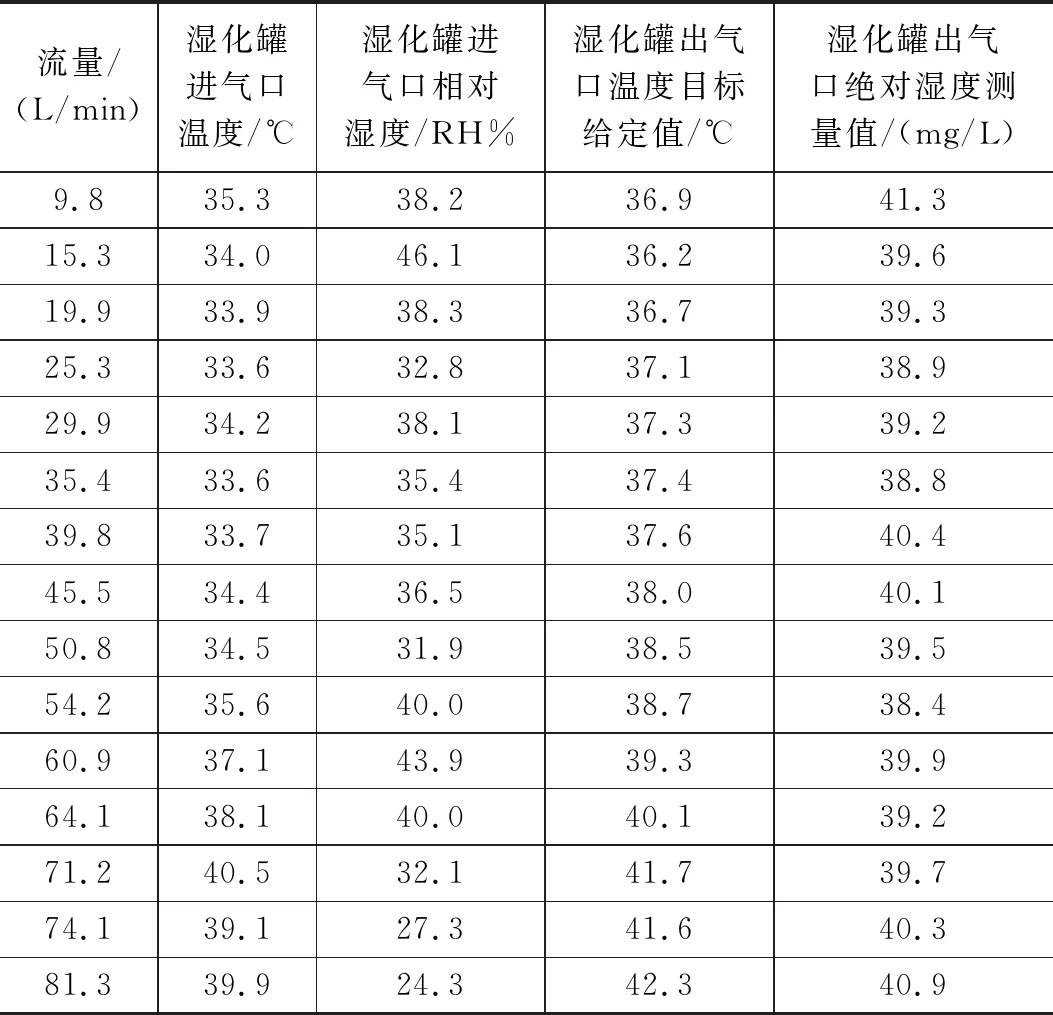
表3 模型检验数据表(绝对湿度期望值为40 mg/L)
当系统稳定时,此时的流量、湿化罐进气口温度和湿化罐进气口相对湿度的测量值基本保持不变,湿化罐出气口的绝对湿度的期望值为定值。把X1流量,X2湿化罐进气口温度,X3湿化罐进气口相对湿度,X4湿化罐出气口绝对湿度期望值带入式(15)的模型中,得出此时湿化罐出气口温度目标给定值。通过智能控制算法控制湿化罐出气口温度达到目标给定值,由表3得出湿化罐出气口温度控制稳定时,湿化罐出气口绝对湿度的期望值和测量值最大误差为1.6 mg/L,此时绝对湿度的控制精度为±4%,满足湿化仪±5%的控制精度要求。本文对湿度的控制方式,可以解决因湿度测量不足引起的湿度控制的问题,对湿度控制的工程应用有指导意义。
3 结束语
本文通过对湿化仪的湿化罐进行机理建模,从理论上对高流量呼吸湿化仪的控制模型进行了分析,但是涉及的热力学参数太多,本文仅分析了机理部分,在后续的研究中将增加检测手段,再进一步辨识模型。在现有的条件下,采用多元线性拟合的方法,建立了湿化罐的回归模型。实验结果表明,控制湿化罐出气口温度可以间接控制绝对湿度且控制精度满足性能要求。
