一种结合矩阵分解和深度学习技术的POI推荐模型
2020-06-29
(西安建筑科技大学 信息与控制工程学院,西安 710055)
0 引言
近年来, LBSN平台吸引了无数用户并产生了大量签到数据。通过对签到数据建模并结合传统推荐技术来实现用户POI的推荐,可以从推荐结果中得出用户的日常喜好和行为模式;帮助商家发现潜在客户、调整经营策略,具有极大的经济和社会效益[1]。
目前,基于LBSN的用户POI推荐研究,无论是基于传统协同过滤、矩阵分解方法还是基于影响因素或文本信息考虑的POI推荐模型均存在以下的问题:
大部分POI推荐研究采用传统协同过滤算法[2-4],对用户和签到的POI进行建模,给出最后推荐。但这种基于LBSN的用户签到信息很容易遭遇数据稀疏问题。又有研究者提出基于矩阵分解的协同过滤算法[5-6]。分别用一个隐式向量代表用户和POI,隐式向量间的内积表示用户和POI之间的线性交互。这些算法有效缓解了数据稀疏问题且对用户和个性化POI特征提取做出改进。但由于隐式向量内积操作只是简单向量间的线性乘法,不足以提取用户和POI之间高阶历史交互特征(非线性特征),尤其是无法捕捉用户签到的序列特征。
为了解决序列建模的问题,有研究者[7]利用矩阵分解和马尔科夫模型建模用户的序列行为,但马氏模型只考虑用户访问的最近一个POI点信息,所包含信息量太少,不能很好表示用户行为特点。深度神经网络能够有效学习和提取多个特征的高阶非线性关系,特别是循环神经网络(RNN)能够很好地对序列进行建模。Q.Liu等人[8]提出ST-RNN模型,Zhao等人[9]改进提出ST-LSTM模型。这类模型虽然能有效建模用户签到的序列行为,但从用户细粒度兴趣来看:单一的RNN无法同时学习用户长期和短期的兴趣特征,从模型整体来看:忽略了多影响因素之间的联合作用。
综合以上问题,文章的具体研究内容如下:1)针对签到数据的稀疏问题,提出一种基于分解矩阵的协同过滤方法。计算得到POI的特征向量;2)针对用户细粒度兴趣(即长期兴趣和短期兴趣)序列建模问题,提出一个基于注意力机制(Attention)的深度神经网络模型。可分别提取用户长、短期兴趣特征[10-11];3)针对多影响因素之间的联合作用问题,将矩阵分解提取的POI特征向量以及计算得到的用户特征向量按照用户签到序列输入带有注意力机制的深度学习网络进行模型训练。设计得到多特征高阶非线性交互的POI推荐模型(MF-ADNN)。该模型可对LBSN中的地理、时间、社交和序列影响进行综合考虑,分别对用户签到数据集的4阶段(早、午、晚、夜)进行训练,做出不同时间段的POI推荐。
1 问题定义和用户细粒度兴趣分析
POI推荐模型旨在为用户推荐其感兴趣的POI点。表1是本文用到的基本数学符号及含义。
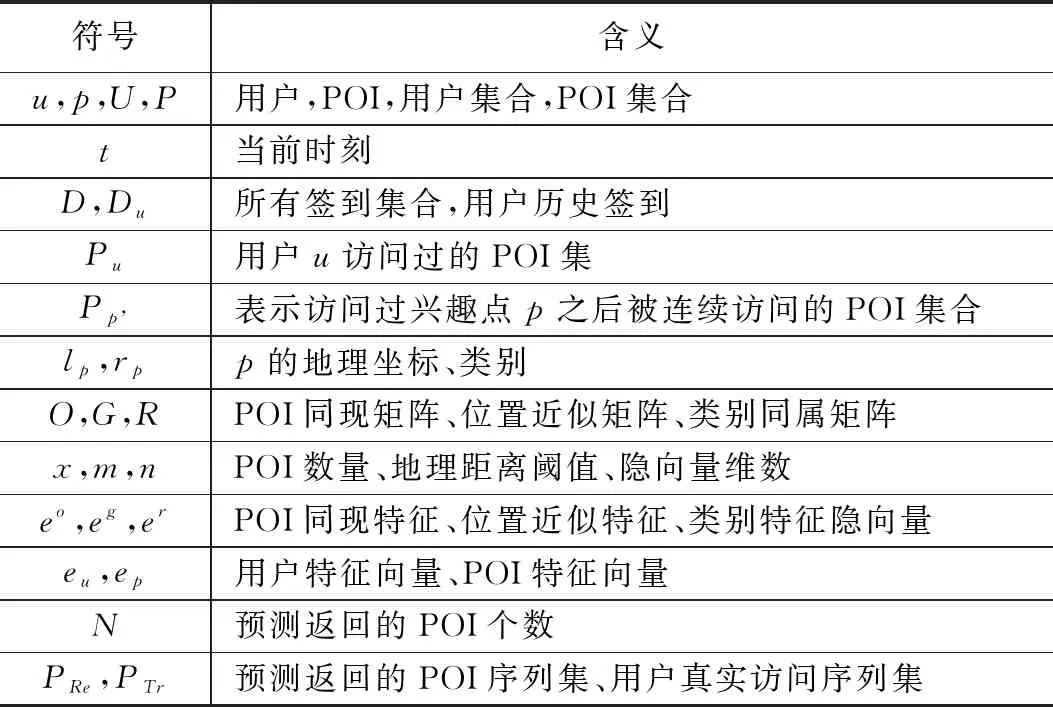
表1 基本数学符号及含义
1.1 问题定义
U={u1,u2,...,un}表示用户集合,P={p1,p2,...,pm}表示兴趣点,给定用户u的历史签到记录Du,当前的时间t,文章所提出的POI推荐模型最终的操作是:从POI集合P中返回N个兴趣点序列{pre1,pre2,...,preN}。序列集pre,即未来某阶段内用户u最有可能访问的兴趣点集。
1.2 细粒度兴趣
用户兴趣随着时间的推移可能会发生变化,即用户签到行为可分为长期兴趣和短期兴趣两种,本文称之为用户的细粒度兴趣。
1.2.1 用户长期兴趣
用户的长期兴趣一般指用户周期性访问的POI。RNN结构具有记忆功能,能够很好地为用户的签到序列行为特征进行建模,对于捕获用户的长期兴趣是一个好的选择。但一般的RNN存在梯度消失的问题,故采用LSTM来捕获用户的长期兴趣。具体模型情况参见第3.3节CF-ADNN模型的LM模块。
1.2.2 用户短期兴趣
用户的短期兴趣最有可能影响后续的兴趣点访问,一般主要指与上一个访问的兴趣点距离和类别相近的POI。故采用带有Attention机制的seq2seq架构。将用户历史兴趣点编码成一个向量,利用Attention机制关注最相近的几个兴趣点进行解码,最终得到用户的短期兴趣。具体模型情况参见3.3节CF-ADNN模型的SM模块。
2 结合矩阵分解和深度学习技术的POI推荐模型
本节介绍结合矩阵分解和深度学习的个性化POI推荐模型CF-ADNN的构建及训练过程。将矩阵分解提取的POI特征向量以及计算得到的用户特征向量作为以上两个模块的输入,构建POI推荐模型CF-ADNN,并对该模型进行训练。
2.1 基于矩阵分解的兴趣点特征表示
为了解决签到数据的稀疏问题,利用签到数据集中兴趣点的ID,地理坐标和所属类别这三个维度信息,建立POI同现矩阵、位置近似矩阵以及类别同属矩阵。再基于一种矩阵分解方法得到POI在同现、位置和类别特征中的隐向量,将上述三种隐向量拼接成一个整体的POI特征向量表示[12]。
2.1.1 构造特征矩阵
1)POI同现矩阵:初始化一个POI同现矩阵O∈Nn×n,表示POI在用户访问模式上的关联关系,n等于POI数。具体来说,Opp′表示同时访问过p和p′兴趣点的用户个数,对角线元素Opp表示访问p的用户个数。一般的,Opp′值越高,表明p和p′频繁地被先后访问,则证明关联性越强。
2)位置近似矩阵:与POI同现矩阵类似,初始化一个位置近似矩阵G∈Nn×n,表示用户的签到行为和POI的地理位置高度关联。引入距离阈值m=10 km,根据签到点的经纬度坐标计算p(lon,lat)和p′(lon′,lat′)之间的距离D,若小于m,则Gpp′=1;否则Gpp′=0。特别的,Gpp=1。D的计算公式:
C=sin(lat)*sin(lat′ )*cos(lon-lon′)+cos(lat)*cos(lat′)
D=R*Arccos(C)*PI/180
(1)
其中:R为地球平均半径6 371.004 km。
3)类别同属矩阵:类别同属矩阵R∈Nn×n,表示POI在类别信息上的关联,利用了POI的内容信息。若p和p′属于同一个类别,Rpp′=1;否则Rpp′=0。特别的,Rpp=1。
构建特征矩阵过程示例如图1所示。
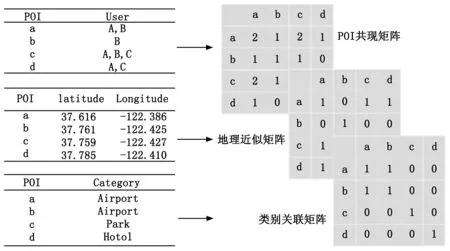
图1 构建特征矩阵示意图
2.1.2 对称矩阵分解
将上述3个对称矩阵进行矩阵分解:
1)POI同现矩阵分解:对于POI同现矩阵O∈Nn×n,把这个矩阵分解成两个矩阵的点乘,如公式(2)所示:
O(n,n)=Eo*ETo
(2)
使两个同阶的矩阵相似程度最小,得到最接近原始矩阵,如公式(3):
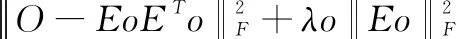
(3)
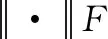
为了进一步说明对称矩阵分解的优点,给出两个POI隐向量的相似度近似计算公式(4)~(5):
(4)
(5)
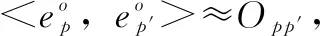
通过观察近似公式可知,隐向量的相似性与用户临近POI访问率有关,说明上述分解方法能够很好地学习、表示兴趣点在该特征空间的相互关联;同时抑制了热门POI对最终推荐结果的影响,有利于POI推荐结果的多样化。
2)位置近似矩阵分解:与POI同现矩阵分解方法相同,具体的分解形式如式(6)所示:

(6)
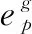
3)类别同属矩阵分解:与上述矩阵分解方法相同,具体的分解如公式(7)所示:
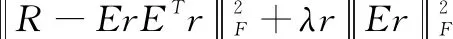
(7)
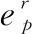
2.1.3 计算特征向量
拼接上述3个矩阵分解所得的隐向量,得到一个整体的POI特征向量表示。具体如公式(8):
(8)
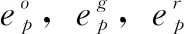
2.2 用户特征向量计算
计算用户特征向量时,可结合考虑用户的社交影响因素,即共同计算用户与用户好友特征向量。文章将用户特征向量表示成该用户与该用户的好友访问过的所有POI的特征向量的期望,从而得到用户特征向量。用户特征向量eu计算公式(9)如下:
(9)
Pu和Pu′分别表示用户u和他的好友u′访问过的POI集合,|Pu|表示用户u访问过的POI数量。
2.3 POI推荐模型CF-ADNN
CF-ADNN模型旨在构建不同的神经网络模型分别学习用户长期和短期兴趣特征。将前两节基于矩阵分解提取的POI特征向量,以及计算得到的用户特征向量按用户签到序列输入模型,训练模型的高阶交互特征,预测未来最有可能访问的兴趣点集。
2.3.1 CF-ADNN模型结构
图2展示了CF-ADNN模型的整体架构。该模型主要分为两个主要模块:LM模块获取的是用户的长期兴趣的隐含向量;SM模块获取的是短期的隐含向量。
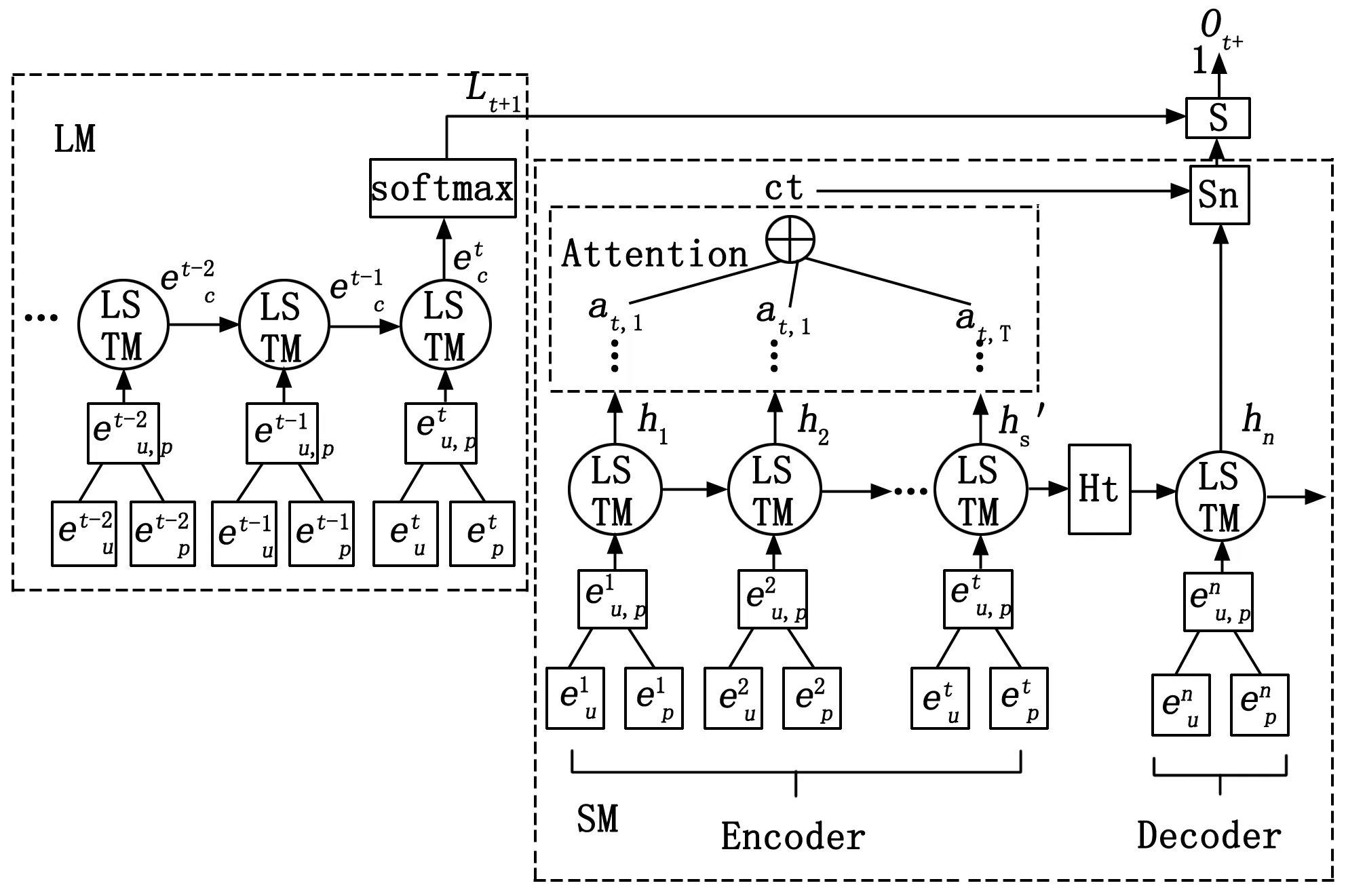
图2 CF-ADNN模型整体架构图
1)LM模块:
用户的长期兴趣主要考虑的是用户周期性访问的模式。为了捕获长期兴趣,采用LSTM来捕获用户的长期兴趣。具体的公式如下:
(10)
(11)
(12)
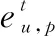
2)SM模块:
用户的短期兴趣主要指与上一个访问的兴趣点相近的(距离和类别)的兴趣点。选择相同类别且两个连续签到点距离小于10 km的兴趣点作为用户的短期兴趣。SM模块采用带有Attention+seq2seq架构,seq2seq架构主要分为Encoder和Decoder。用户的短期兴趣表示方法:通过Encoder把用户访问的兴趣点编码成一个向量,编码方式选择LSTM网络。编码过程公式如下:
(13)
(14)
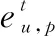
具体公式如下:
Ct=∑sαtshs
(15)
(16)
score(hn,hs)=vTtanh(ω1hn+ω2hs)
(17)
其中:vT、ω1和ω2是模型需要学习得到的参数。这里Ct最为重要,表示通过Attention计算得到的上下文向量。进一步计算得到引入注意力的隐藏状态向量:
Sn=f(Ct,hn)=tanh(Wc[Ct+hn])
(18)
以及解码器生产的目标兴趣点序列:
S[yt|{y1,y2…yt-1},Ct]=softmax(WcSn)
(19)
长期兴趣Lt+1以及短期兴趣序列St+1结合起来,得到最终的推荐结果Ot+1:
Ot+1=Lt+1∪St+1
(20)
2.3.2 推荐模型训练
从时间维度分析,为了训练一个模型来适应不同时间段的用户签到,这里将签到数据分为4个时间段:夜(0∶01-6∶00)、早(6∶01-12∶00)、午(12∶01-18∶00)、晚(18∶01-24∶00)分别进行训练,得到适应不同时间段的POI推荐模型。
CF-ADNN推荐模型学习算法
输入:eu、ep、t、T
输出:Ot+1(最终的推荐结果)L(最小损失值)
1.Repeat
2.Foreachu∈UDo
3.输入eu和ep,SM训练用户短期兴趣S
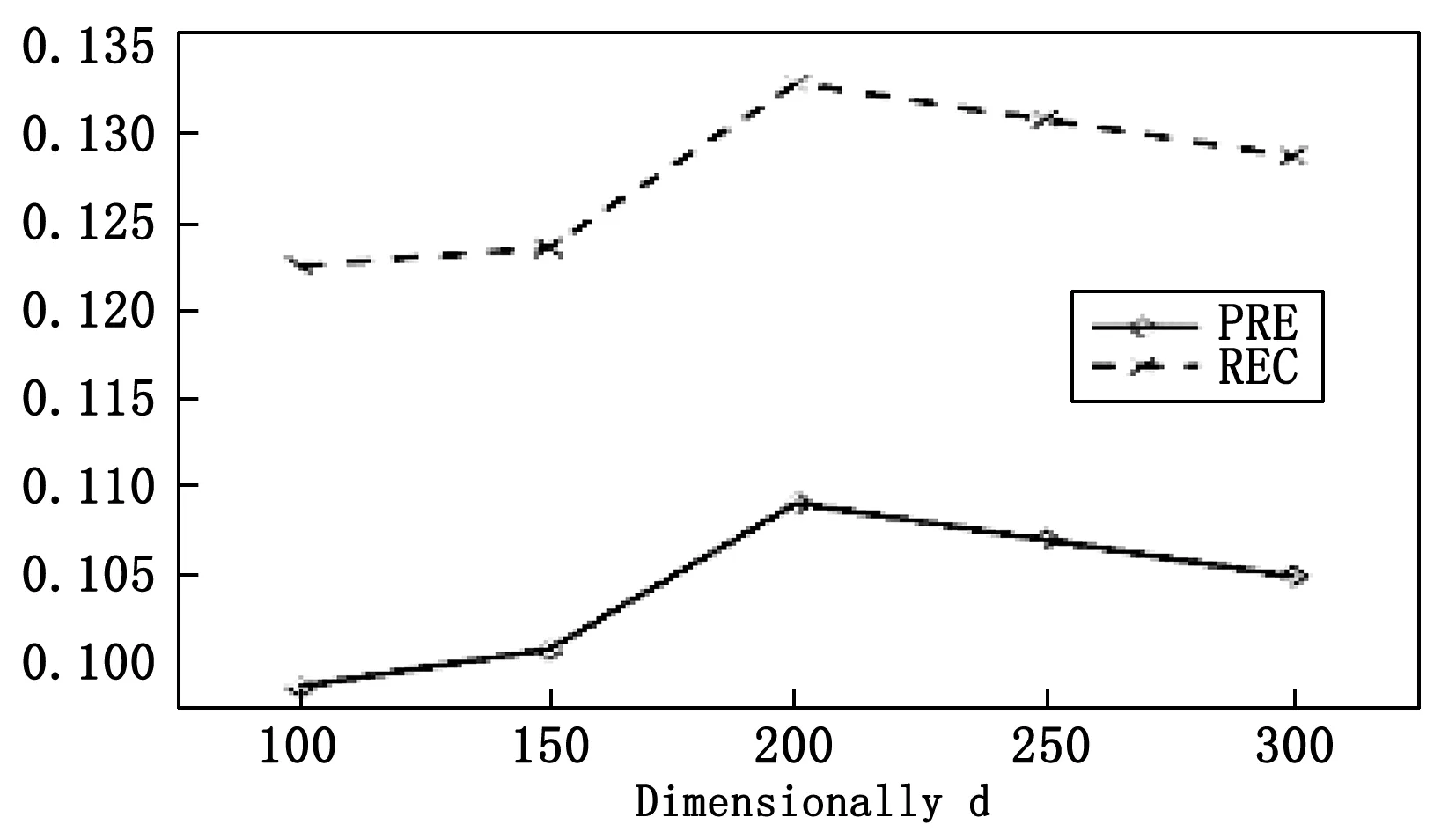
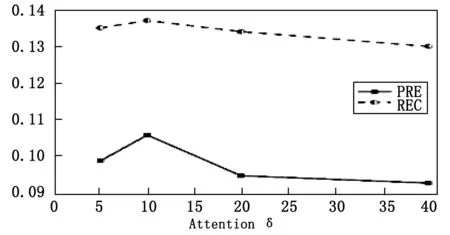
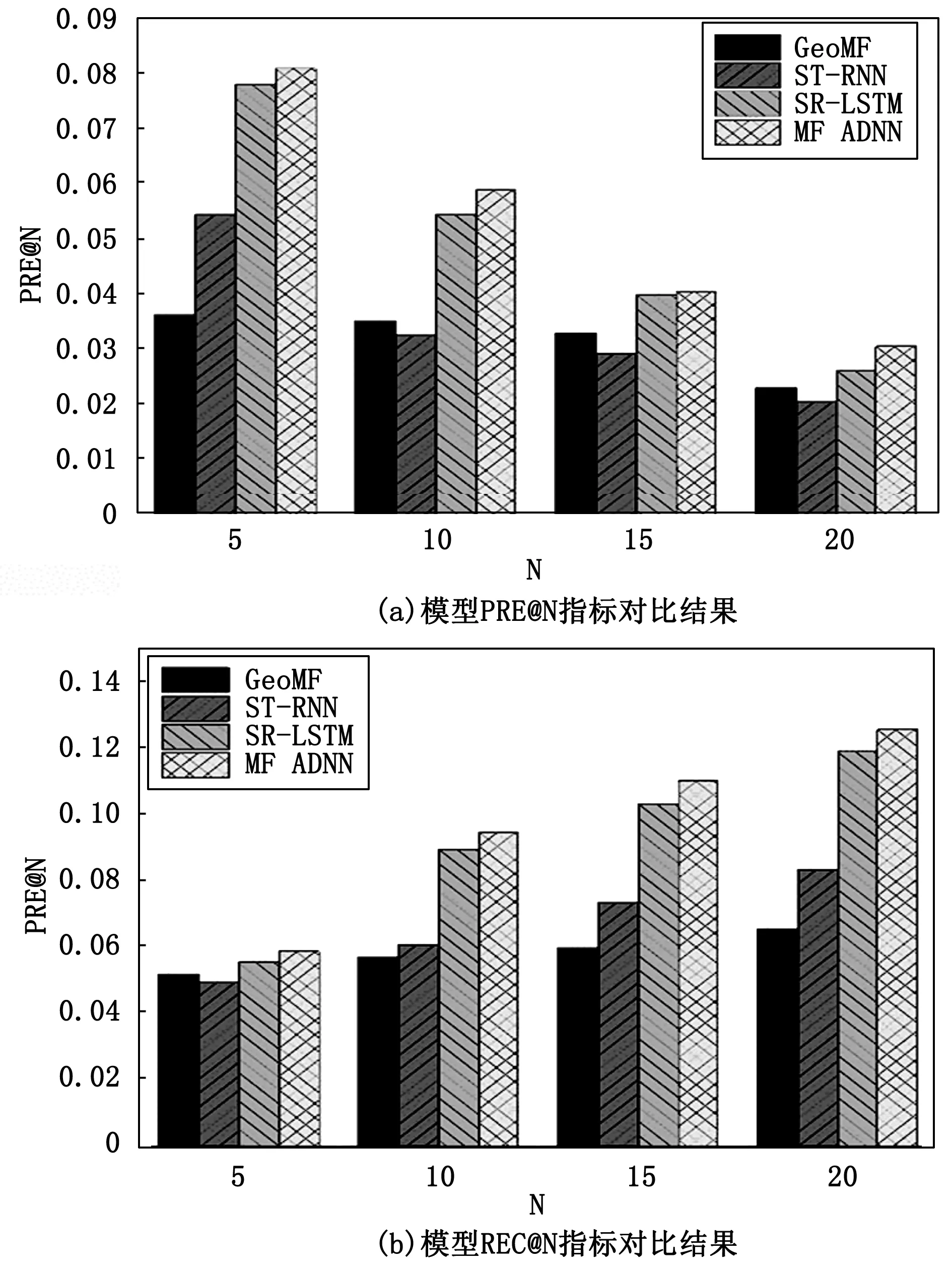
4.Fort 5.输入eu和ep,LM训练用户长期兴趣L 7. End for 9.梯度下降法最小化损失lu 10. ift>Torlu足够小 11.End for 12.Returnlu、Ot+1 13.End procedure 本文采用Foursquare签到网站的开源数据集作为实验数据,验证模型的有效性。选取美国旧金山市(SFO)的用户签到信息,统计结果如表2所示。 表2 用户签到信息统计表 训练时,将用户前80%的签到数据集作为训练集,最近的20%作为测试集。 性能评价指标选用准确率、召回率,分别用PRE@N,REC@N表示。对于一个用户u,模型的推荐结果是: (21) 用户真实的访问序列是: (22) 其中:N为模型预测返回的POI个数。 则准确率和召回率的公式如下: (23) (24) 3.3.1 参数影响 训练模型时选取的参数会对推荐结果造成影响。本文主要讨论影响模型最重要的两个参数: 1)特征向量维度d:eu和ep作为模型的输入可以看出,特征向量维度d是影响整个模型的重要因素。d越大模型需要的计算量越大。 图3 特征向量维度d对模型影响 固定矩阵分解中的正则项参数λo=λg=λr=0.000 01,设置维度d为100、150、200、250、300。实验结果如图3所示,当维度超过200后模型的性能开始降低,故本实验将d设置成200。 2)关注长度δ:用户短期兴趣建模主要用到基于Attention机制的序列模型,Attention关注长度δ对模型十分重要。δ过长,模型会变得复杂;δ过短,可能会使得数据不足。 图4 关注长度δ对模型影响 分别设置关注长度δ为 5,10,20,40 进行试验,实验结果如图4所示,当δ为10模型效果最好。 3.3.2 不同推荐模型对比结果 为了验证CF-ADNN模型的性能,文章选择3个在矩阵分解和深度学习POI推荐算法领域,具有代表性的模型进行试验对比。GeoMF[5]:基于矩阵分解的地理位置信息POI推荐;ST-RNN[8]:基于时空上下文RNN模型的POI推荐;ST-LSTM[9]:基于时空上下文LSTM模型的POI推荐。 CF-ADNN模型与以上3种算法的性能对比结果如图5所示。 图5 算法性能对比结果图 从图5的对比结果可知,GeoMF模型的指标率最低。这说明基于矩阵分解方法的POI推荐模型虽然有效缓解了数据稀疏性,但由于隐式向量内积操作只是简单向量间的线性乘法,不足以提取用户和POI之间高阶历史交互特征尤其无法捕捉用户签到的序列特征。而ST-RNN和ST-LSTM模型将用户的历史签到记录用序列方式传入RNN来学习用户及POI的向量表达,可有效建模用户签到的序列行为,故推荐性能指标明显高于GeoMF模型。同时,ST-LSTM模型对ST-RNN进行改进,避免了梯度消失,故ST-LSTM模型推荐性能优于ST-RNN。而MF-ADNN结合矩阵分解技术和带有注意力机制的用户签到序列建模技术,可以降低签到数据的稀疏性;细粒度建模用户兴趣;更好学习联合影响因素的高阶非线性交互特征。因此与其它3个模型相比,MF-ADNN在准确率和召回率上均有更优的表现。 文章提出一个结合矩阵分解和带有注意力机制深度学习技术的POI推荐模型。该模型融合了时间影响、地理影响、社交影响以及序列影响4个因素实现用户POI推荐。主要任务包括:通过构建特征矩阵缓解签到数据稀疏问题,矩阵分解得到隐藏因子,计算POI的特征向量;构建一种带注意力机制的用户细粒度兴趣的序列建模方式,有效学习用户长期和短期的兴趣特征,提高POI推荐精确度;结合上述两种方法,最终得到可以融合多种影响因素的POI推荐模型。试验结果表明,该POI推荐模型具有较好性能。文章未考虑的影响因素还有很多,如评论信息、文本信息等,未来的工作将考虑在模型中融入这些特征,进一步提升推荐算法的性能。
3 实验与分析
3.1 实验数据集
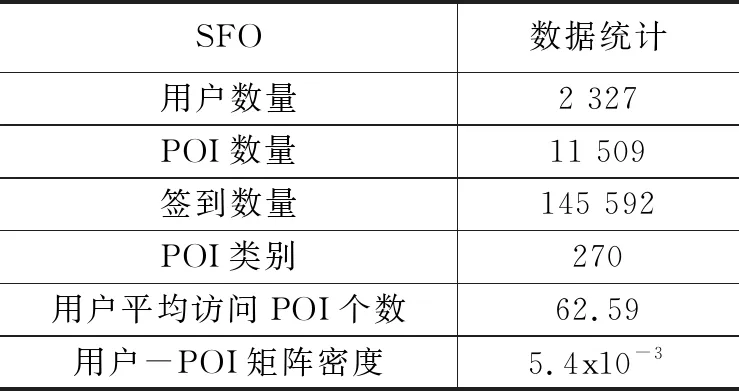
3.2 评价指标
3.3 实验结果及分析
5 结束语
