激光雷达风速模拟系统设计
2020-06-29
(中国人民解放军92942部队, 北京 100161)
0 引言
风场是重要的气象参数和大气动力学参数,与气候变化及各种异常气候现象的发生有密切的关系,高时空大尺度的精细风场探测技术的研究一直是激光雷达遥感的重要研究目标及前沿技术之一。
多普勒测风激光雷达是目前进行大气风场测量的最有效的工具之一,为了保证激光雷达风场测量的准确性,需要对其进行正确合理的定标。而对于瑞利散射测风激光雷达,由于大气分子后向散射谱的特殊性,直接对其风速标定比较困难,在考虑频移量产生的同时还需要考虑目标散射谱和大气分子散射谱的一致性,所以采用风速模拟装置并选择合适的鉴频器搭建实验系统显得尤为重要[1]。通过比较目前非相干多普勒测风激光雷达的鉴频器,Fabry-Perot(F-P)标准具及机械式Mach-Zehnder(M-Z)干涉仪在光通量、透过率、最小视场角的优势。采用机械式M-Z干涉仪作为鉴频器具有透过率高、视场宽及大光通量的特点,但同时其体积大、稳定性差[2],光纤M-Z干涉仪作为鉴频器可实现高稳定性和小型化,为新型小型化多普勒激光雷达发展以及建立星载平台上全球风场探测激光雷达提供新的技术支持及解决方法[3]。
本文基于光纤M-Z干涉仪测风激光雷达研究基础,设计并搭建风速模拟探测激光雷达的自校正式实验系统,重点采用能量探测方法对鉴频系统性能进行实验分析,进一步研究利用全光纤M-Z干涉仪实现大气风场探测的关键技术, 完成实际大气风场探测激光雷达的系统标定。
1 光纤M-Z干涉仪的多普勒测风激光雷达系统原理及鉴频特性分析
1.1 系统结构及原理
多普勒测风激光雷达系统的结构如图1所示。系统对风速的探测过程为:采用种子注入技术的激光器以一定重复频率射出波长为532 nm的激光光束,经扩束、准直后通过分光镜BS分成两路,其中一路参考光束经透镜耦合进光纤M-Z鉴频系统光纤1臂中,最后由PMT1和PMT2检出,经放大后送入示波器和工控机中,注意此时将频率锁在光纤M-Z干涉仪两透过率谱线交点位置。
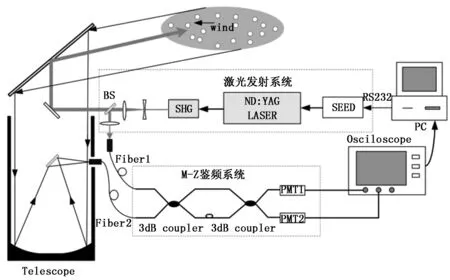
图1 多普勒测风激光雷达原理图
由BS分光后的另一路由全反射镜整合,直接射入大气风场中,激光束中大气分子热运动和气溶胶粒子布朗运动会产生多普勒展宽,将其等效为空气柱,空气柱的整体移动产生多普勒频移,其后向散射光脉冲信号(大气回波信号)由望远镜接收,经光纤传输给窄带干涉滤光片,滤除背景噪声光后耦合进光纤M-Z鉴频系统的光纤2臂中,此时测量信号相比于参考信号比较微弱,其干涉信号由PMT1和PMT2经光电转换、放大后送入示波器采集并显示,最终在工控机中进行风速反演。由于透过率有陡峭的光谱响应,因为测量信号频率与发射信号频率的微小变化,通过滤波器后,对应光纤M-Z透过率强度不再相同,得到光强的较大变化,即光功率的变化,从而使光强变化直接相关到频率的变化,达到鉴频目的[4]。本系统设计探测风场范围为0~20 m/s低层大气风场,探测误差小于1 m/s。
回波信号光强分布函数为I(σ),而光纤M-Z干涉仪两通道滤波器透过函数分别为T1(σ)、T2(σ),通过两者进行卷积得到两通道输出函数S1(σ)、S2(σ):
S1(σ)=sI(σ)⊗T1(σ)
S2(σ)=sI(σ)⊗T2(σ)
(1)
其中:s是探测器灵敏度,这里设s=1,I(σ′)为:
(2)
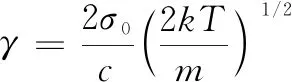
则光电探测器PMT1和PMT2接收到信号为:
S1=
S2=
(3)
其中:δ为光程差倒数,对于光纤M-Z干涉仪δ=1/nL,L为臂长差,n为光纤折射率。
计算差分信号为:
(4)
考虑到风速引起的多普勒频移,风速u与后向散射光的波数关系:
(5)
那么优化后的风速u的响应函数为:
(6)
对信号进行统计学分析,假设两通道输出信号S1(σ)、S2(σ)都有很好的信噪比(使用一组脉冲累加数据),则有:
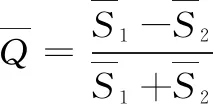
(7)
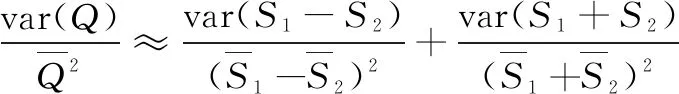
(8)
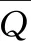
(9)
SNR是两通道信噪比之和:
(10)
则风速标准差为:

(11)
这里假设光纤M-Z干涉仪传输损耗是固定,SNR与鉴频器的参数无关,若使εu达到最小值的必要条件就是使表达式 (1+Q2)(dQ/dv)-1的值达到最小,即使Q值最小并且dQ/du值最大。
1.2 系统光程差和探测灵敏度分析
在完成了多普勒测风激光雷达系统的结构设计后,需对系统关键参数进行仿真分析,光纤鉴频系统作为测风激光雷达系统的核心组成部分,其光程差的选取直接影响风速响应灵敏度和风速探测范围。这里根据光程差和灵敏度之间的关系,模拟不同光程下的风速灵敏度和回波信号函数,找到适合系统探测范围内的最佳风速响应趋势。
根据风速u和Q响应函数公式(6),对风速求导得到单位风速下差分信号的变化率,即风速灵敏度:

(12)
在保证零频移探测灵敏度最高,同时正负向风场探测范围对称的前提下,根据双边缘技术大气风场探测原理,发射激光中心波长应位于光纤M-Z干涉仪两通道透过率强度曲线边坡最陡峭处,设定入射中心波长λ=532 nm,参考温度T0=250 K,光纤有效折射率n=1.46,两臂光程差必须满足在中心波长位置两通道信号强度相等,即S1=S2,此时:
(13)
满足此方程的光程差1/δ均为最优光程差。由于不同高度上大气风场从0 m/s到上百米每秒之间变化,选取零风速、20 m/s、100 m/s和580 m/s的风速值,图2为绘制在不同风速时探测灵敏度随最优臂长差的变化情况,横坐标为满足Q=0的最优臂长差值(ALD)。可见不同风速下探测灵敏度随最优臂长差变化,在0 m/s条件下,其灵敏度最大值(图中A点)为1.8%(m/s),对应臂长差为74.8 cm;在100 m/s条件下,灵敏度为零时对应的最小臂长差(图中B点)为13.7 cm;在580 m/s条件下,灵敏度为零时对应的最小臂长差(图中C点)为2.35 cm,即实验室现有光纤M-Z干涉仪臂长差值。
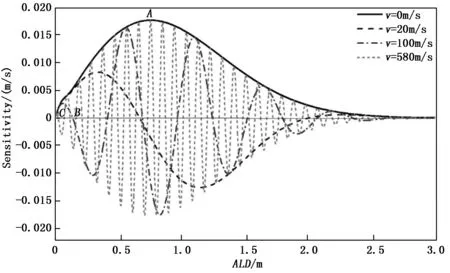
图2 灵敏度与最优臂长差关系曲线
分别取最优臂长差ALD的值74.8 cm、13.7 cm和2.35 cm代入风速响应函数Q中,响应函数值Q对应不同风速变化趋势如图3所示。零风速下响应函数Q值均在零点,可以看出当ALD=74.8 cm时,响应函数值Q随风速变化更迅速,响应函数曲线更陡峭,曲线的1/2周期所对应的风速值决定了风速探测范围,风速探测动态范围为±18.2 m/s,可以实现风速的精细探测,满足低空大气风场下的模拟风速变化范围要求。当ALD=13.7 cm时,响应函数Q对应风速变化比较缓慢,对风速响应不积极,风速动态变化范围大,达到±100 m/s,适合中高层大气探测。实验室现有的ALD=2.35 cm的光纤M-Z干涉仪,其由于光程差较小,在3个曲线中对风速响应趋势最缓慢,风速探测灵敏度最低,而且风速测量范围大于500 m/s,并不适于本系统用于大气风速探测。
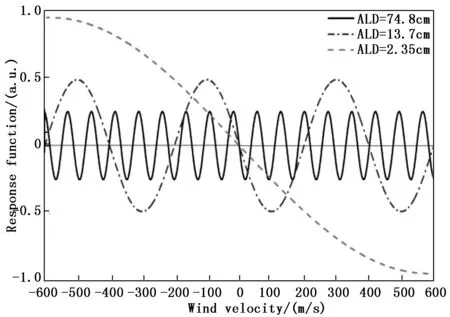
图3 回波信号函数Q随风速分布图
再分别对最优臂长差为74.8 cm、13.7 cm和2.35 cm组成的鉴频系统对风速灵敏度进行分析,则鉴频系统在ALD=74.8/13.7 cm和ALD=2.35 cm时,其动态风速探测范围内的风速探测灵敏度分布如图4、5所示。
图4 鉴频系统风速探测范围内的灵敏度分布图(ALD=74.8/13.7 cm)

图5 鉴频系统风速探测范围内的灵敏度分布图(ALD=2.35 cm)
ALD=74.8 cm的鉴频光路可实现高灵敏度(最大1.8%/(m/s))、小动态范围(±18.2 m/s)探测,ALD=13.7 cm的鉴频光路可实现中灵敏度(最大0.78%/(m/s))、较大动态范围(±100 m/s)探测,ALD=2.35 m的鉴频光路可实现低灵敏度(最大0.25%/(m/s))、大动态范围(±100 m/s)。根据仿真结果可知,随着光程差减小,风速探测范围随之增大,而对风速响应的灵敏度则逐渐变小。
因此根据低层大气风场探测(±20 m/s内)要求,本系统选取74.8 cm最优臂长差,可得到探测范围内的最佳风速响应趋势。
2 风速模拟探测激光雷达的自校正式实验系统整体结构设计与搭建
由于非相干多普勒测风雷达系统在测风时会产生测量误差,因此设计一套校正系统,通过模拟的风速,由确定的多普勒频移反推灵敏度方法来校正系统测量风速,其原理如图6所示。采用种子注入技术的激光器射出的波长为532 nm的激光光束通过分束镜,分成两路,其中一路参考光束经透镜L1耦合到光纤M-Z鉴频系统,最后由光电探测器PMT检测,作为参考信号。另一路光直接射向以一定角速度旋转的转轮上,转轮的线速度引起入射光多普勒频移,透镜L2收集后向散射光,经过光纤反向传输到鉴频系统,由光电探测器PMT检测,在示波器中以能量形式显示,进行模拟风速校正。通过对示波器上不同时刻检测到的光电探测器信号能量变化按上述公式进行反演,可得转轮的线速度。
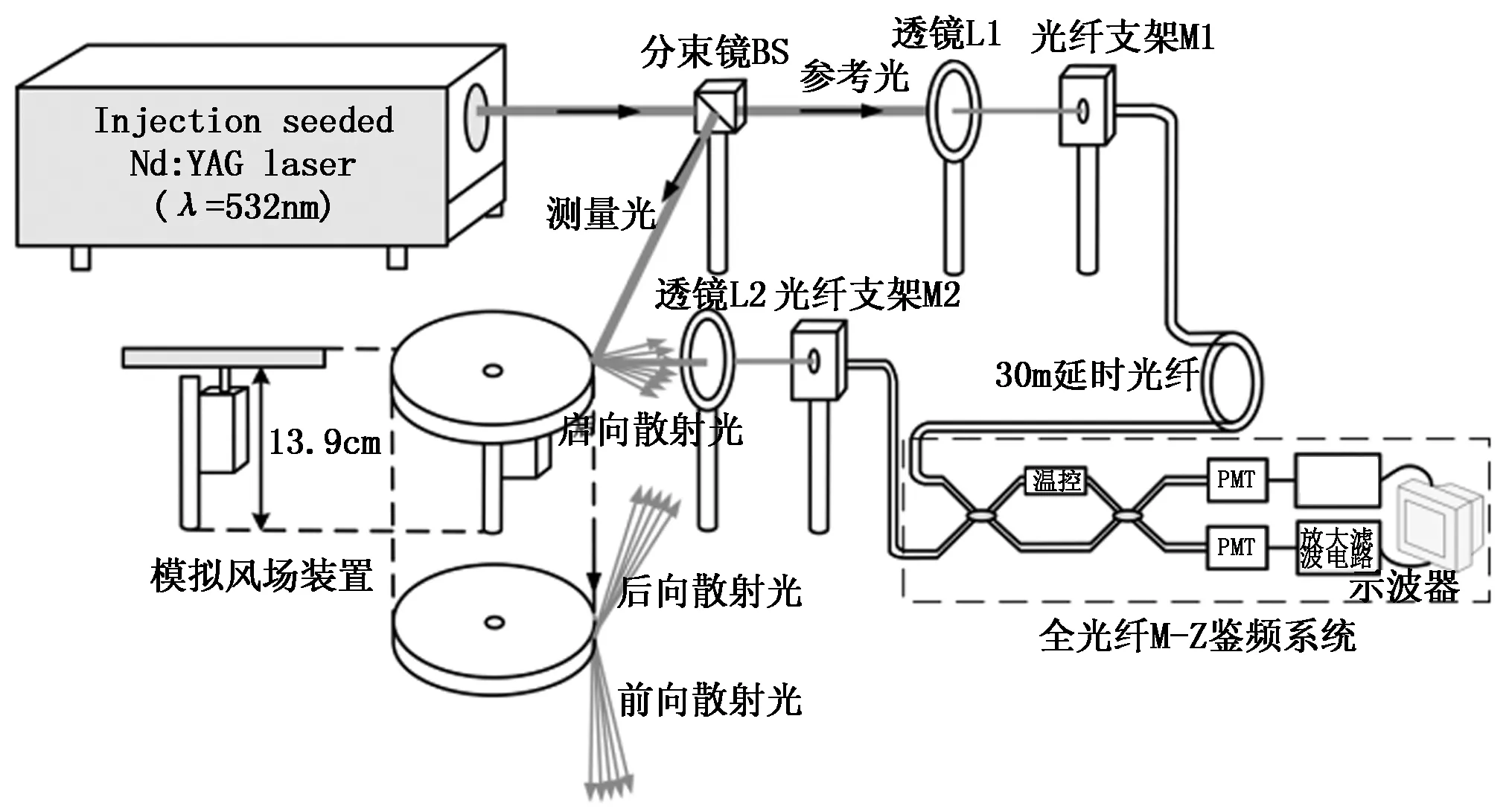
图6 自校正式实验系统结构框图
全光纤M-Z鉴频系统通过两个光纤耦合器熔接进行制备,按照74.8 cm的最优臂长差值进行熔接,实际测量光纤M-Z干涉仪臂长差为76.5 cm,如图7所示。
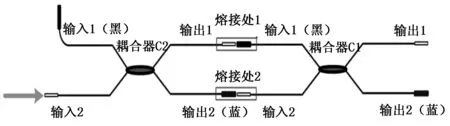
图7 全光纤M-Z干涉仪
模拟风场系统由电机和转轮平台构成。电机选用全数字式松下A5II系列伺服电机,额定转速3 000 r/min[6]。转轮直径为200 mm,因激光器光束直径为9.5 mm,转轮厚度选为10 mm,通过AutoCad进行设计并机械加工。
光电探测系统由两个Metal Package-H6780系列03型光电倍增管组成,有低纹波噪声和快速定位特性。
3 风速模拟探测激光雷达实验及数据分析
3.1 光纤M-Z干涉仪光程差校正实验
在进行风速模拟探测前,先通过能量探测方式验证光纤M-Z干涉仪透过率谱强度曲线。按照最优光程差选取分析,采用臂长差粗测值L0为0.023 5 m的全光纤M-Z干涉仪,又知光纤折射率n为1.46,可得光程差值:
L光程差=n·L0=1.46·0.0235=0.03431 m
(14)
这里取σ0为1/532.087 5,大气温度T为250 K,代入S1、S2和Ⅰ(σ)计算公式(2)和式(3),则两通道透过率强度分布通过Matlab软件仿真结果如图8所示。
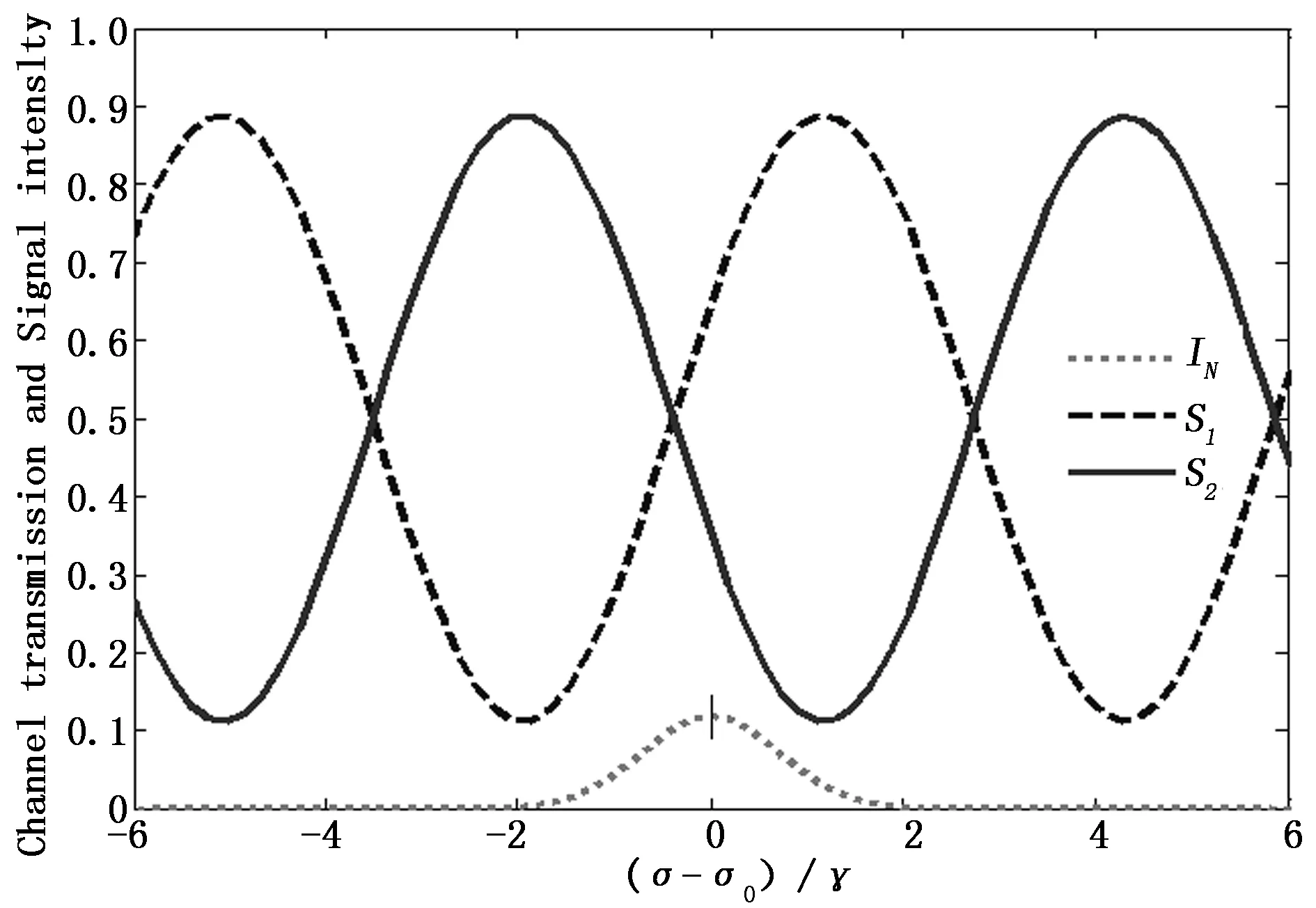
图8 光纤M-Z干涉仪两通道透过率强度
S1、S2透过率强度曲线自由光谱范围是6.142 8 m-1,此时绿色的分子入射谱线中心位置没有位于透过率强度分布曲线S1和S2的交点,通过差分计算S1和S2值可以反演风速,但透过率强度曲线的自由光谱范围受光程差影响较大,微小的光程差变化可能带来较大的周期变化,因此需要利用种子激光器模拟多普勒频移过程,通过绘制透过率强度分布曲线对应的自由光谱范围来反推精确的光程差值。
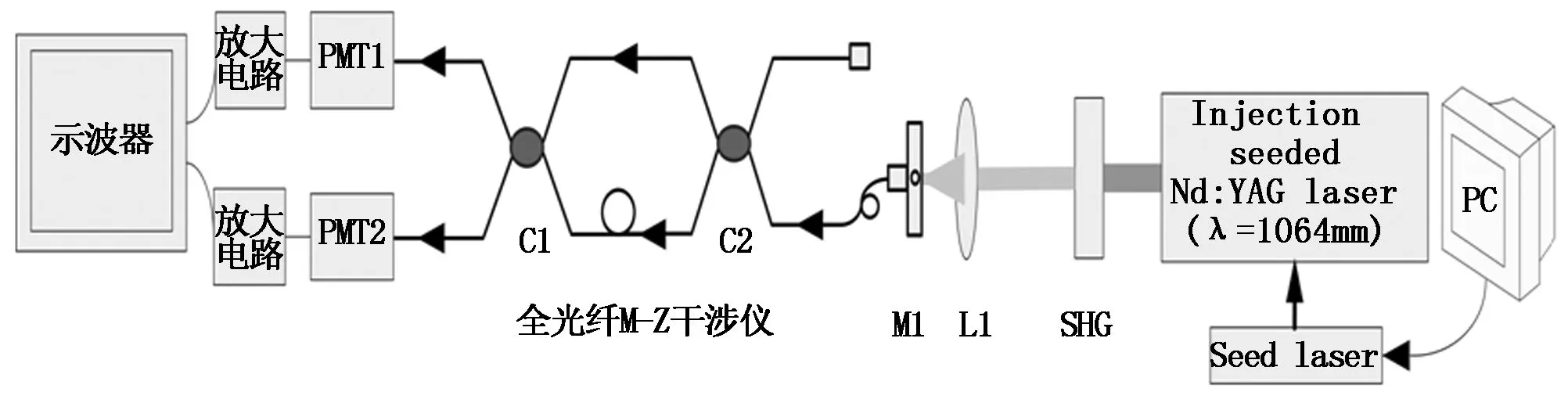
图9 光纤M-Z干涉仪光程差校正实验方案
利用自校正式系统的一部分器件搭建实验,方案如图9所示,激光器输出532 nm激光,经透镜L1耦合如光纤M-Z干涉仪一臂(另一臂封闭),干涉光的光强信号经过PMT1、PMT2和放大电路后转换为能量信号,通过调整种子激光器波长,记录示波器在不同波长位置的两通道能量变化值,从而绘制透过率强度分布曲线,反推光程差。
将种子激光器通过RS232串口线与控制计算机连接,打开种子激光器波长调试软件,进入操作主页面如图10所示。

图10 种子激光器操作主界面图
将波长从1 064.189 nm调整至1 064.131 nm,间隔0.002 nm采点,σ0选取调整范围中间值为1/(1 064.161×10-9),实际二倍频后波长是从532.094 5 nm间隔0.000 5 nm调整至532.080 nm,σ0为1/(532.087 5×10-9)。通过对测量点进行正余弦拟合可得到波长和透过率强度曲线关系,如图11所示。
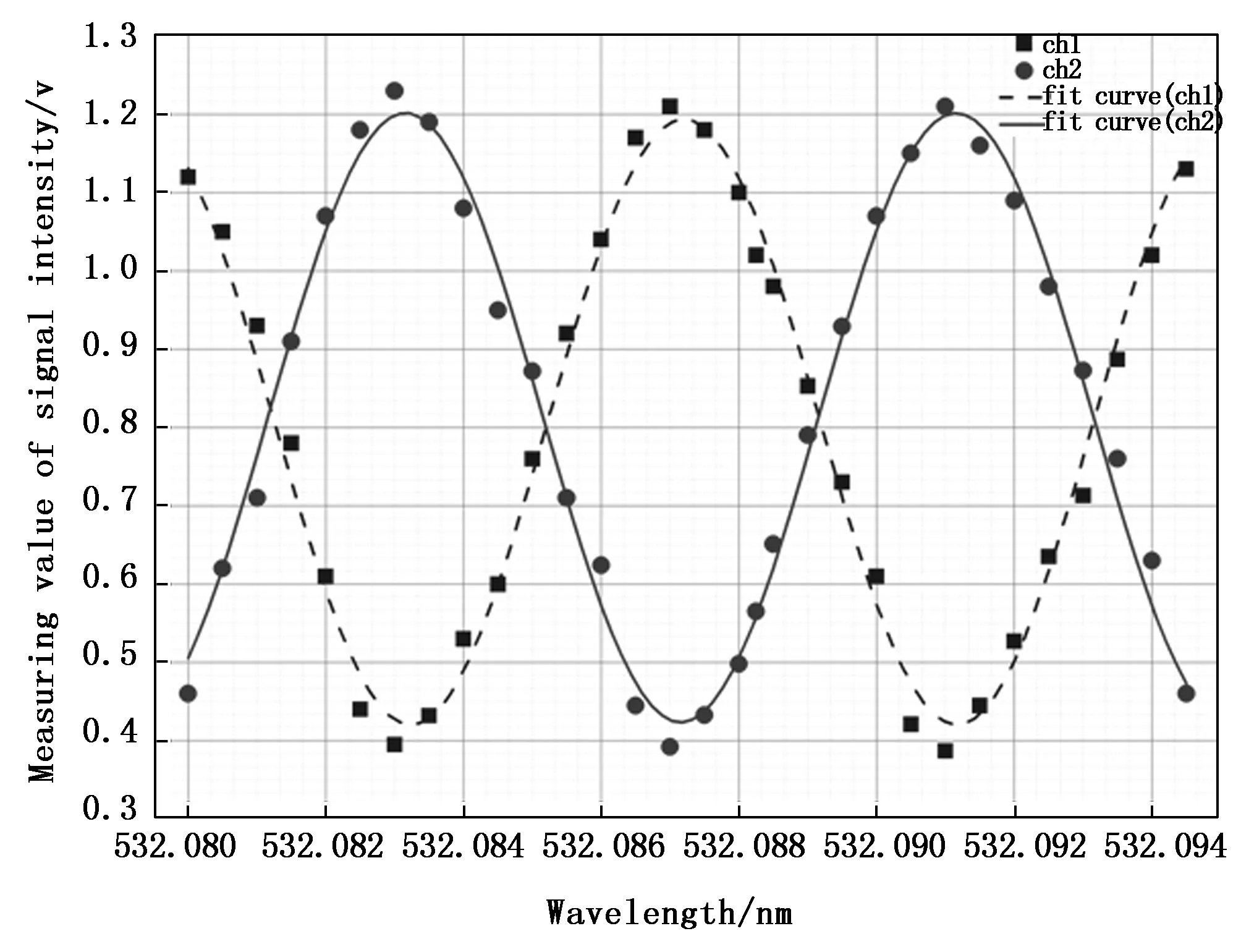
图11 透过率强度测量值拟合曲线图
可以看到透过率强度曲线呈正余弦变化趋势。为了便于和仿真图对照,将拟合曲线横坐标变为(σ-σ0)/γ计算,得到透过率强度拟合曲线变形图,如图12所示。
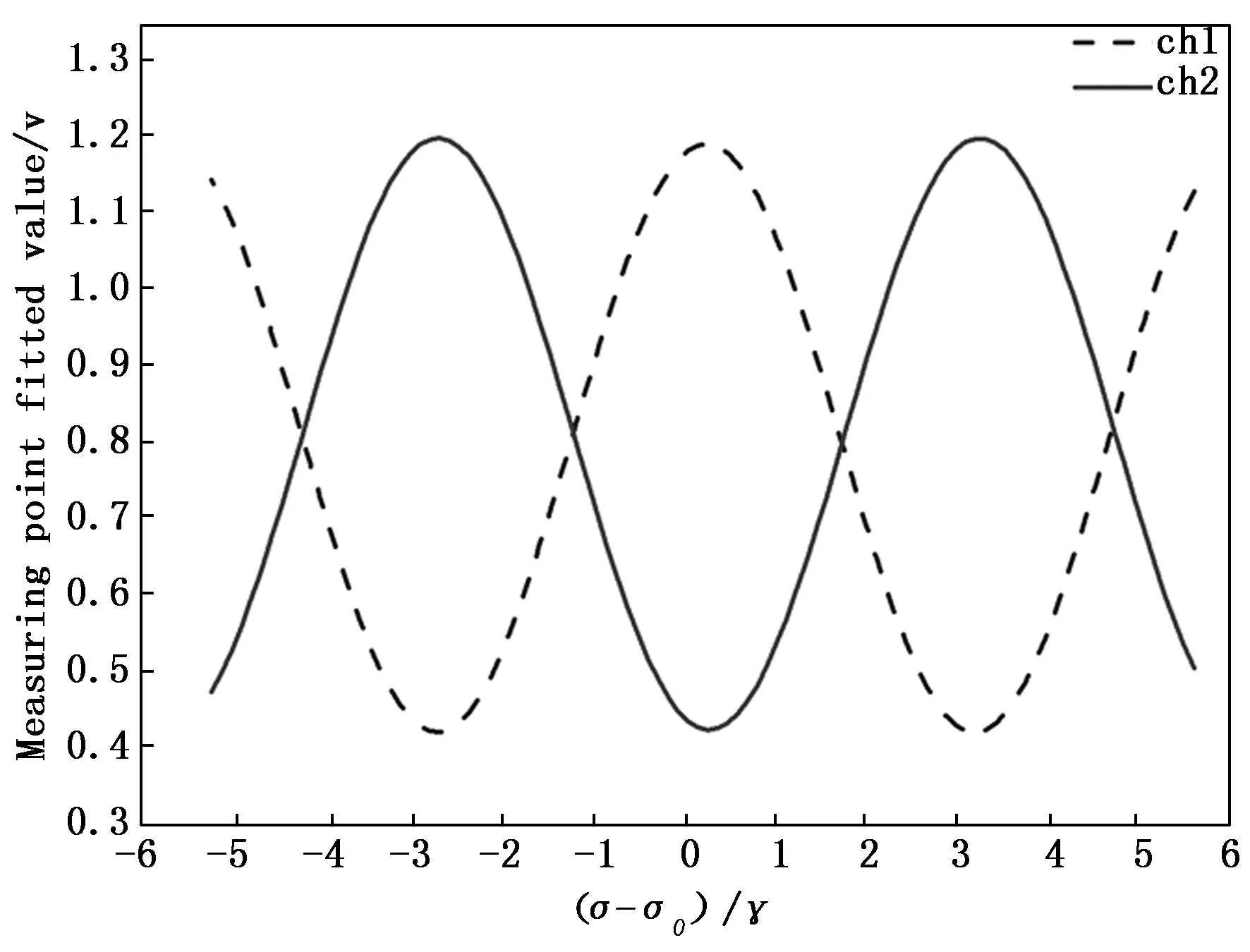
图12 透过率强度拟合曲线变形图
透过率强度曲线的自由光谱范围是5.919=m-1,S1、S2透过率强度曲线交点偏移零点1.721=m-1。通过Matlab软件代入公式2.30反推臂长差为0.023 898 872 5 m,将此臂长差值带入S1、S2计算公式得到校正后的透过率强度曲线仿真图(如图13所示)。经与透过率强度拟合曲线对比,自由光谱范围相等,验证了反推的光程差值。
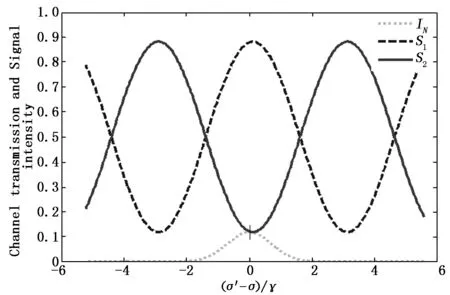
图13 校正后的透过率强度曲线图
3.2 风速模拟探测实验
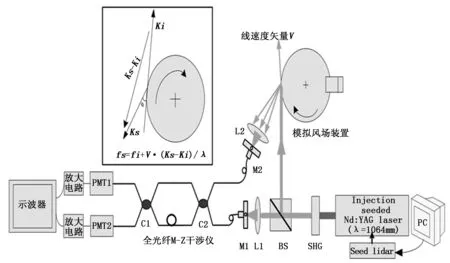
图14 风速模拟探测实验方案图
为了验证风速与Q的关系,利用自校正式实验系统进行风速模拟探测实验,在测量模拟风场前,示波器中PMT1、PMT2输出线接入C2、C3通道,示波器出现两脉冲信号。通过PC端启动种子调整波长位置,找到两通道脉冲能量值相等的位置,此时激光频率恰好位于透过率曲线交点,光纤M-Z干涉仪的透过率强度相等。经实验发现种子激光器波长调节到1 064.170 nm位置时,示波器检测到脉冲能量近似相等的波形,如图15所示,通道C2和通道C3能量差为6.4 mV。即认为此中心波长指向透过率曲线交点位置附近。
电机转速从-2 000 r/min(逆时针旋转)每隔100 r/min调整到2 000 r/min(顺时针旋转),可计算出电机带动转轮旋转的线速度变化范围为-21~21 m/s间隔0.1 m/s变化。调节到指定转速稳定后,对每个转速下示波器C2、C3通道能量值做1 000次平均,并记录平均值。
3.3 模拟风速反演和误差分析
因为实验室环境中激光入射到转轮侧面散射光的多普勒频移主要由米散射引起,而米散射大小又主要由激光器线宽决定,这里看成γ和γm相等为0.5,La表示熔接的光纤M-Z干涉仪臂长差值为76.5 cm,那么风速响应函数为:
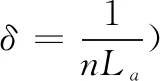
(15)
由风速响应函数可计算仿真值Qs,得到Qs随风速u变化关系;将两通道输出总能量值归一化校正,差分计算两通道能量值得到实际值Qa,通过Qa值可得反演风速值Vi。实验数据如表1所示。
模拟风速对应Qa和Qs变化趋势如图16所示,Q的实际值和理论值变化趋势基本吻合,模拟风速在风速响应函数Q一个周期内线性变化范围为-17.9~17.8 m/s。每个设置的模拟风速Vs对应的实际反演风速Vi分布,如图17所示。
可观察到随模拟风速增加和反演风速值对应成线性递增趋势,对反演风速值进行线性拟合,得到拟合直线的斜率为0.999 2,即反演风速与模拟风速相关性为0.999 2。模拟风速与反演风速两者的偏差分布情况如图18所示。
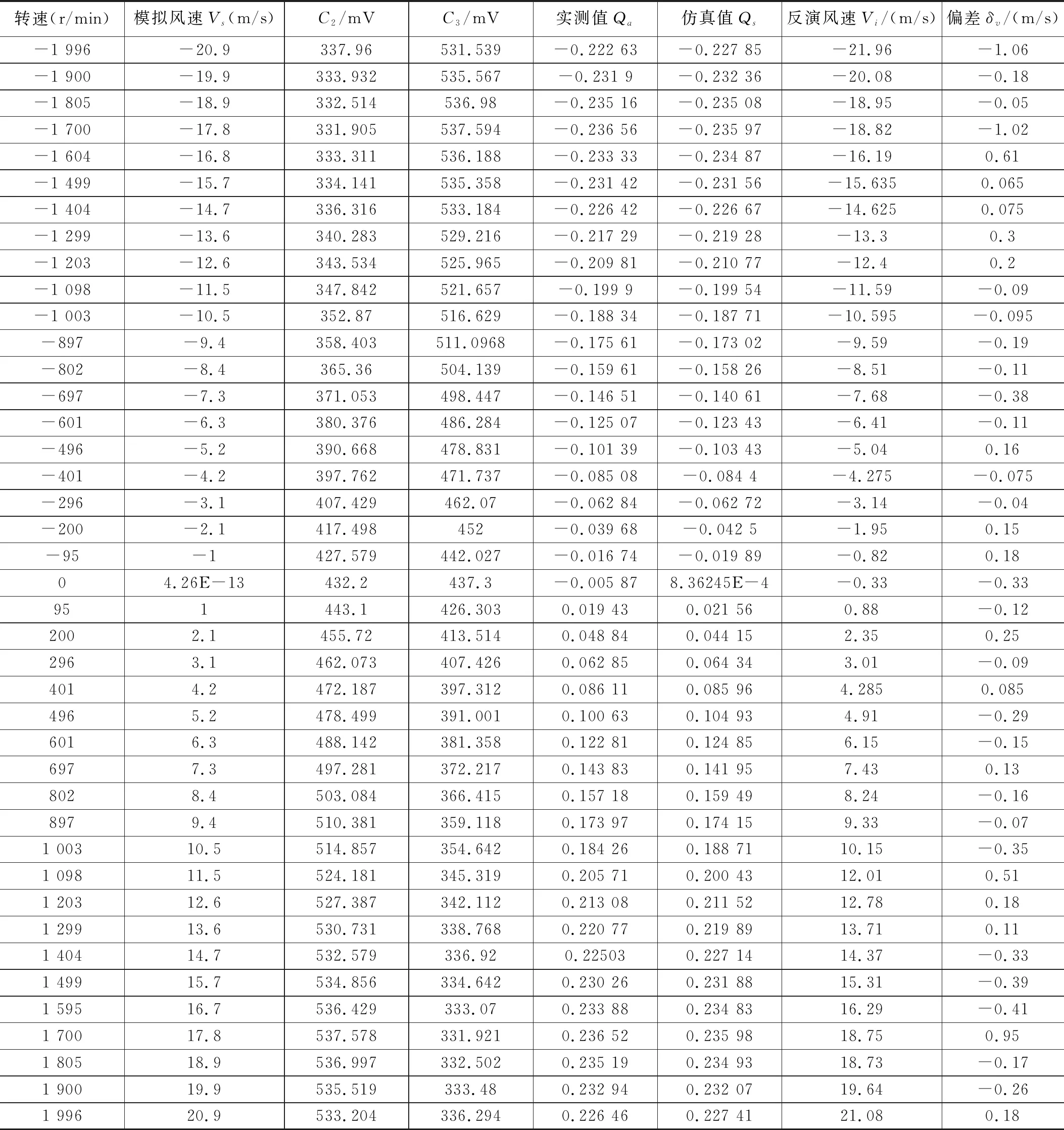
表1 实验数据
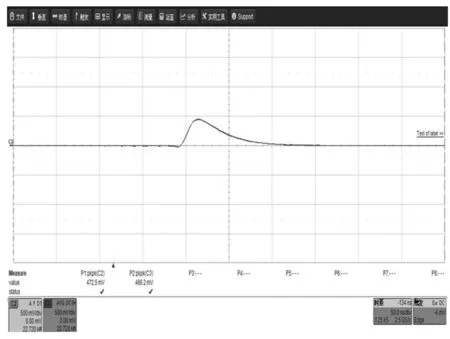
图15 1 064.170 nm位置示波器显示状态
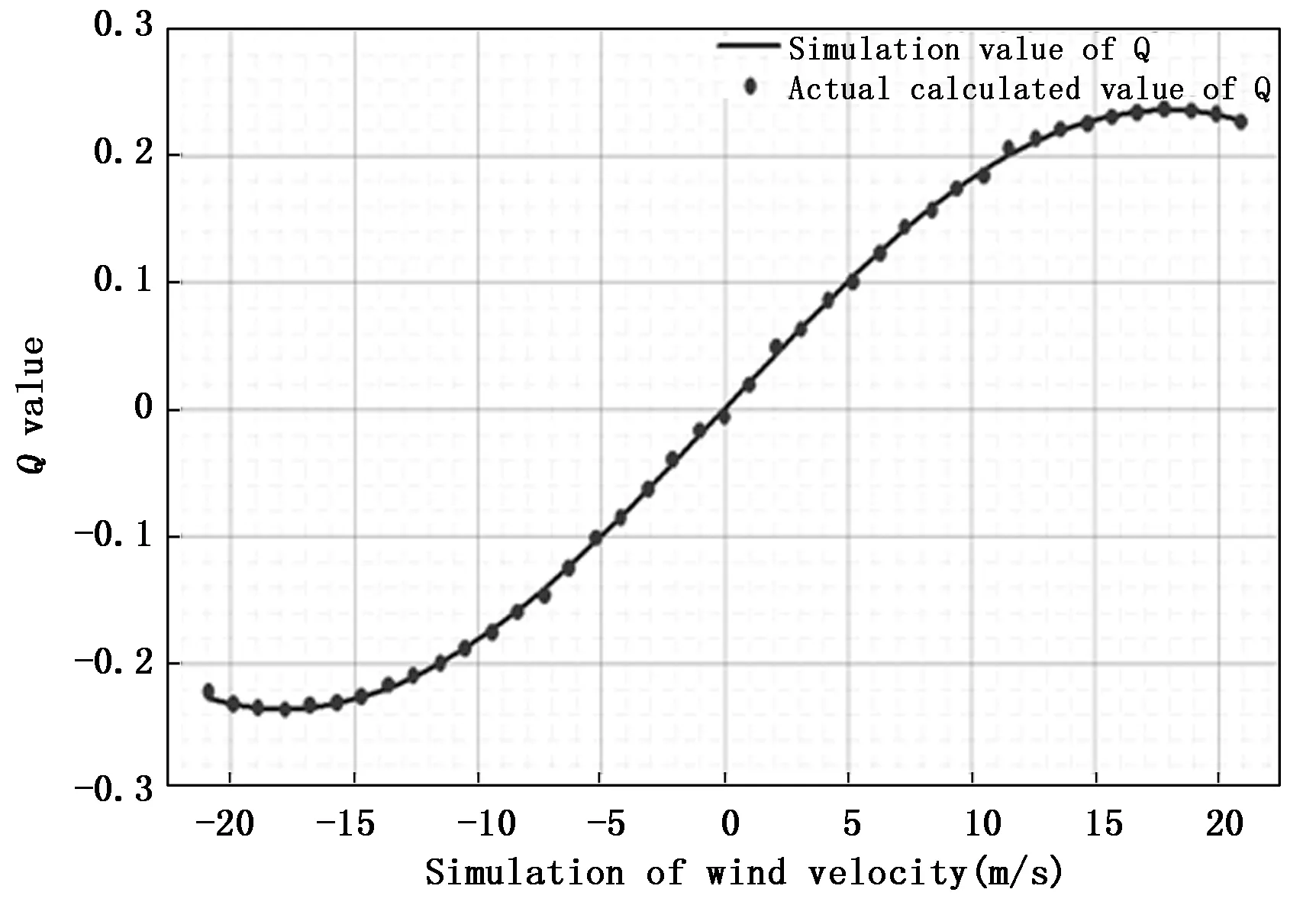
图16 Qa和Qs风速响应图
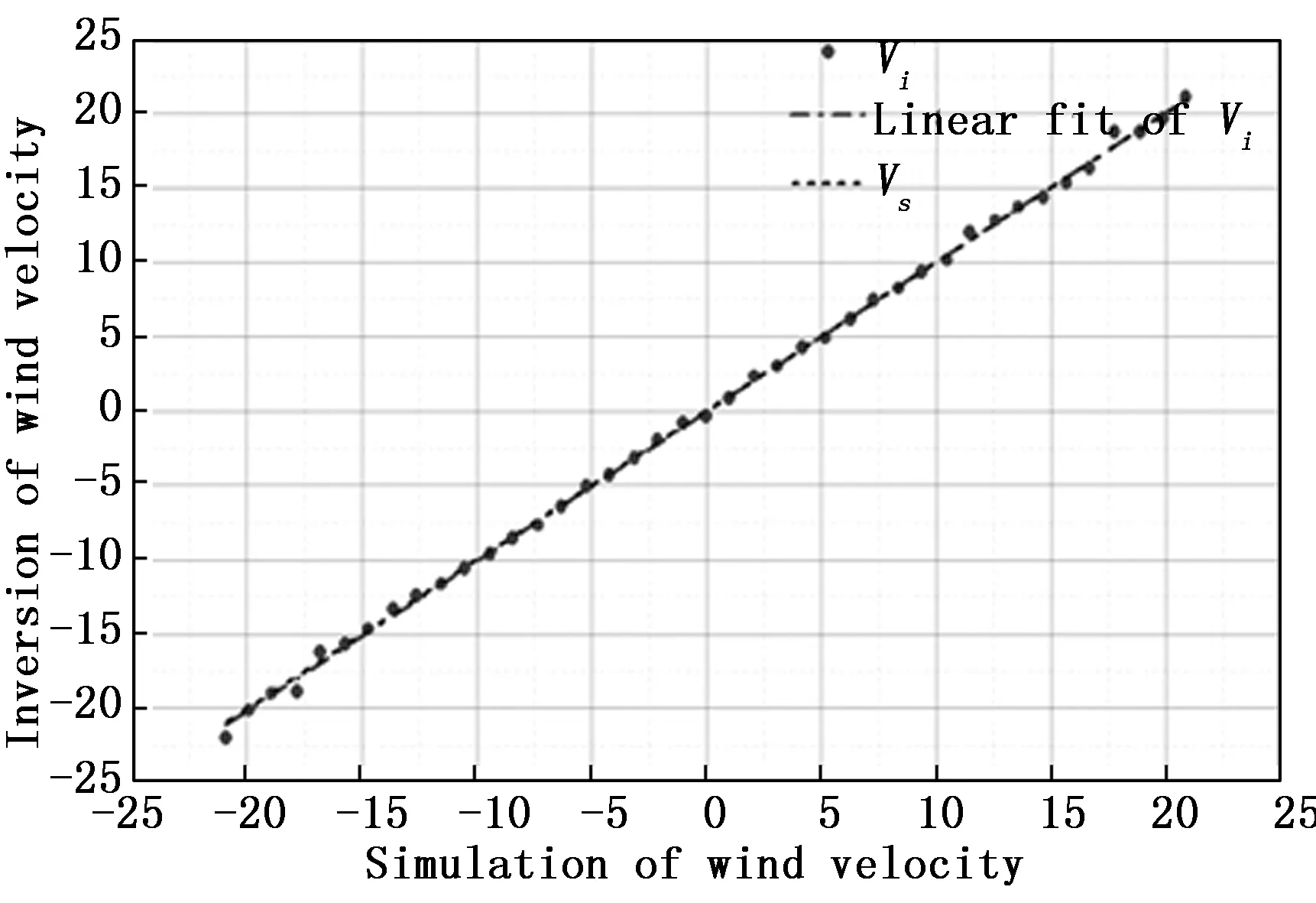
图17 模拟风速Vs对应反演风速Vi分布曲线土
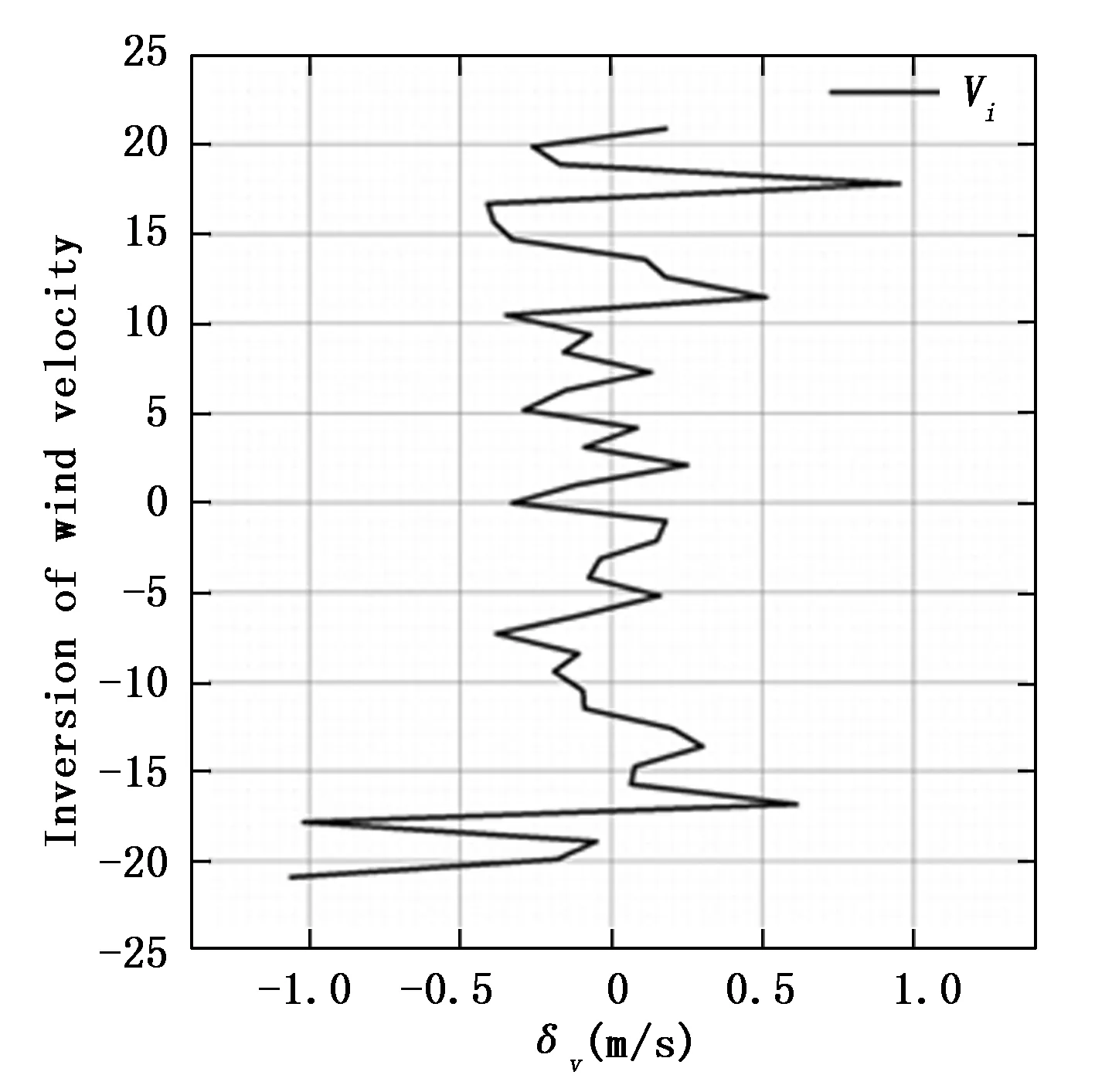
图18 反演风速与理论风速偏差分布曲线

分析偏差主要来自以下几个方面:微小的光纤M-Z干涉仪光程差误差、电机转速误差±1 r/min(换算成线速度0.021 m/s)、探测器暗电流引起的噪声。而风速探测线性范围的分布不对称主要是由于激光频率没有严格位于透过率强度曲线零点位置导致。
4 结束语
本文基于多普勒测风雷达测风原理,采用光纤M-Z干涉仪作为鉴频器,使用光电倍增管作为能量探测器,设计并搭建了激光雷达风速模拟探测自校正式实验系统。利用自校正式实验系统进行光程差精确校正实验,通过种子激光器调节波长模拟多普勒频移过程,在各个波长位置记录两探测器通道能量值,绘制了光纤M-Z干涉仪透过率强度谱线,证明鉴频性能可靠,校正了光纤M-Z干涉仪的精确光程差值。完成了模拟风速探测实验,通过能量值差分计算反演得到不同转速下模拟的风速,系统满足设计要求。验证了风速模拟探测激光雷达的自校正式实验系统的设计理论和方法的可行性。
