基于电阻抗谱特性与集成神经网络的天然气水合物饱和度软测量模型
2020-06-29曹胜昌邢兰昌伟2韩维峰2牛佳乐
曹胜昌,邢兰昌,魏 伟2,韩维峰2,牛佳乐
(1.中国石油大学(华东)控制科学与工程学院,山东 青岛 266580)(2.中国石油勘探开发研究院新能源研究所,河北 廊坊 065007)
0 引言
天然气水合物又称为“可燃冰”,是一种新型优质的潜在能源,是在低温、高压等条件下形成的一种类冰状、具有笼形结构的固态化合物[1-2],通常分布在大陆永久冻土带和海洋沉积物中,具有非常巨大的能源和经济价值[3-4]。天然气水合物饱和度是水合物储层评价的主要参数之一,为认识水合物富集成藏规律、估算水合物资源量提供了必要的基础参数[5-7]。
水合物饱和度是含水合物沉积物电学特性的直接影响因素之一。周锡唐等[8]研究了甲烷水合物生成与分解过程中电导性的变化,实验结果表明电阻随石英砂中水合物生成量的增加而增大,随水合物的分解而急速减小,通过参考温度和压力的同步变化特征证明了使用电导性来监测甲烷水合物生成与分解过程的可靠性。陈玉凤等[9-10]研究了南海沉积物中甲烷水合物饱和度与电阻率的关系,发现在水合物生成过程中,其电阻率会随着水合物饱和度的增加而增大,而且含水合物沉积物存在非阿尔奇现象,其饱和度指数随水合物饱和度的增加而增加。
基于电学特性参数计算含水合物饱和度的模型主要有阿尔奇公式、含泥质修正的阿尔奇公式、印度尼西亚公式和双水模型等,其中阿尔奇公式和含泥质修正的阿尔奇公式被广泛应用[11-13]。Riedel等[14]通过分析不同地区的测井数据,得到了不同的阿尔奇公式经验参数并估算了水合物的饱和度,指出不同地区阿尔奇公式经验参数的差异会导致水合物饱和度预测结果的不同。Spangenberg等[15-17]首先从理论上研究了水合物含量对体系电阻率性质的影响,之后采用溶解气在均匀玻璃珠内开展了甲烷水合物生成实验,测量结果显示电阻率增大系数与含水饱和度之间的关系不能用恒定饱和度指数的阿尔奇公式来描述。含水合物沉积物的电学性质受到沉积物孔隙结构、孔隙水化学成分及浓度、孔隙度、饱和度、温度等多种因素的影响,水合物饱和度与电学性质参数呈现出显著的复杂非线性、多值对应关系,以阿尔奇公式为代表的经验公式的适用性受到极大局限。
神经网络具有强大的处理复杂非线性问题的能力以及高度自学习和自适应的能力,运用神经网络来建立预测模型成为一种有潜力的水合物饱和度计算方法。吕琳[18]等人在使用地球物理测井数据预测储量参数方法的基础上,选用中子测井、密度测井等8种测井数据作为BP神经网络的输入量,预测了天然气水合物的储量参数(孔隙度、饱和度),结果表明该模型计算结果的精度高于传统的经验公式。陆敬安[19]等利用神狐海域某井的电阻率测井数据作为样本训练并建立了径向基神经网络模型,利用该模型计算出另一口井的水合物饱和度,其计算结果与现场孔隙水分析得到的饱和度值相吻合。现有的研究存在以下问题:(1)仅仅利用单个神经网络建立天然气水合物饱和度的计算模型,模型的可靠性有待进一步验证与提高;(2)神经网络的输入参数缺少必要的预处理,导致神经网络模型的准确度受到限制。
本文提出基于集成神经网络方法建立一种以电阻抗谱特性参数为特征向量的水合物饱和度软测量模型,即将不同频率的阻抗模值作为单个BP神经网络的输入,通过对不同位置传感器所对应的子网络输出进行集成,建立基于集成BP神经网络的水合物饱和度计算模型。
1 天然气水合物模拟实验
采用了自主设计的天然气水合物电学探测实验装置开展实验工作。实验装置的总体结构如图1所示,该装置分为环境模拟部分和测试部分。环境模拟部分包括耐高压反应釜、低温冷却系统、天然气气瓶、中间储气罐、轴压系统等,可以模拟出天然气水合物的生成分解所需的温度和压力条件、提供充足的气源以及必要的存储空间等;测试部分主要包括电学传感器、温度传感器、压力传感器、电学测试单元、温度测试单元、压力测试单元、工控机及测试软件,能够实时获取反映水合物生成分解过程动态变化的实验数据。
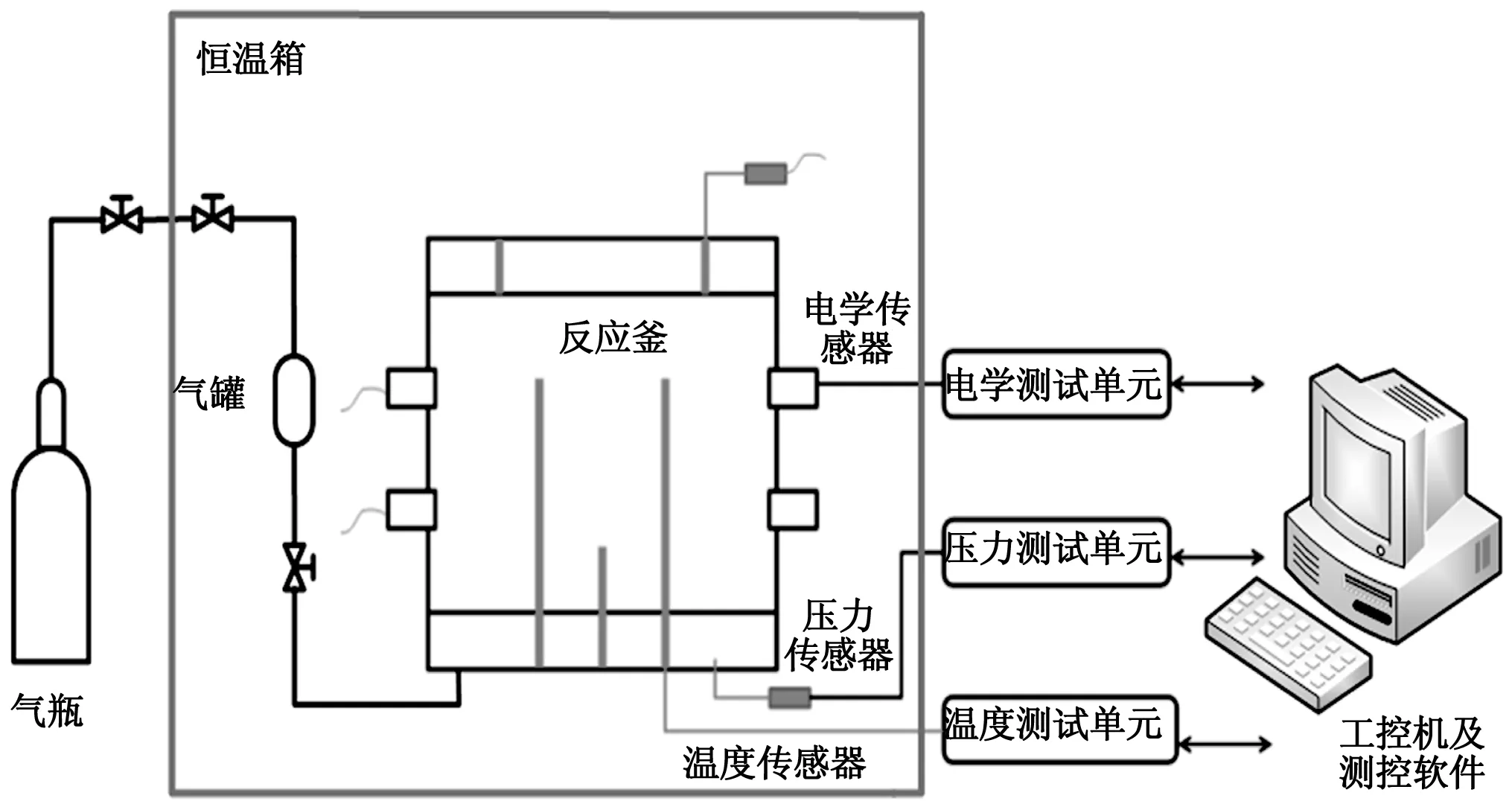
图1 实验装置总体结构
天然气水合物在反应釜内呈现出空间不均匀分布的特性,为了获取水合物的空间分布信息,将电学传感器分为上下两层均匀安置在反应釜壁,每一层安装8个传感器(如图2所示),采用分时轮流工作模式控制各传感器的工作状态。
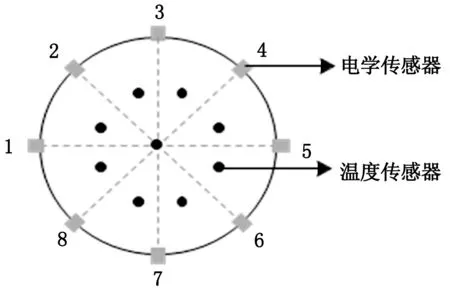
图2 单层传感器排列方式图
利用上述装置开展了甲烷水合物生成分解模拟实验,分析了多孔介质(粒径50~180 μm的天然海沙)中甲烷水合物生成和分解过程中电学特性的变化规律,以及水合物饱和度对含水合物的多孔介质的电学特性影响,在此基础上利用阻抗模值等特征参数建立起特征参数与饱和度之间的软测量模型。
2 神经网络样本集的确定
2.1 数据预处理
实验获得的阻抗谱包括了从1 Hz~10 MHz范围内的22个频率点,但由于系统误差、环境干扰等因素影响,其中一些频率点的数据会出现较大的无规律波动和明显偏差,经过筛选、剔除等步骤对数据进行选择。最终选择出5 Hz、10 Hz、20 Hz、100 Hz、200 Hz、500 Hz、1 kHz、2 kHz、4 kHz、10 kHz、20 kHz、40 kHz等12个频率点作为特征频率点,以这些测试频率点的阻抗模值作为备选的特征参数。
上述特征频率点的原始数据中往往存在噪声值、缺失值以及离群点等情况,不能直接用于软测量模型的建立与测试,因此需要对原始数据进行预处理。数据预处理主要针对数据在数值上的各种异常情况进行处理。本文中数据预处理所采用的步骤为:数据离群点修正处理、数据去噪处理和数据归一化处理。
数据离群点修正处理针对原始数据中远离一般水平的极端大值和极端小值,采用均值插补修正法,根据数据曲线的整体趋势对数据进行估计值的修改,即用异常值数据所处位置左右相邻两个数据的平均值来替代异常值。本文采用小波去噪和滑动平均滤波去噪相结合的方式对数据进行去噪处理,以便获得更好的去噪效果。数据归一化处理将原始数据映射到0~1范围之内,如式(1):
(1)
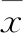
2.2 特征提取
确定特征频率点后,需要针对每组传感器对在多频率下的阻抗模值进行特征提取,即降维处理。通常神经网络输入为多维数据,计算复杂度随着数据维数的增大成指数增加[20],数据维数过大会导致网络训练时间大大增加,也会导致训练后的神经网络性能变差。
本文采用主成分分析法(PCA)进行降维处理,消除不同频率间阻抗模值之间的相关性,降低网络输入的维数、精简网络的结构,采用累计贡献度达到99%的主成分作为神经网络的输入。
2.3 形成样本集
2.3.1 水合物饱和度计算
在甲烷水合物模拟实验中,基于耗气量原理计算水合物饱和度,即利用实时采集的反应釜内温度和压力数据并结合式(2)进行计算:
(2)
式中,Sh为水合物饱和度;P1为反应釜内初始压力;P2为水合物生成分解过程中反应釜内压力;T1为反应釜内初始温度,T2为水合物生成分解过程中反应釜内温度;Z1和Z2为对应压力温度条件下的气体压缩因子;Vg为反应釜气相体积;Mh为水合物摩尔质量,122.02 g/mol;R为气体常数,8.314 J/(mol·K);ρh为水合物的密度,0.91 g/mL;Vp为多孔介质孔隙的体积。图3为一轮典型实验中水合物生成分解过程中温度、压力以及水合物饱和度的变化曲线。
在水合物生成分解过程中,上层1-5传感器对在部分特征频率点(20 Hz、200 Hz、2 kHz、20 kHz)下的阻抗模值随水合物饱和度变化的关系如图4所示。通过分析阻抗模值参数与饱和度参数之间的关系可以发现,阻抗模值随着饱和度的增加逐渐增大,呈现出显著的非线性。
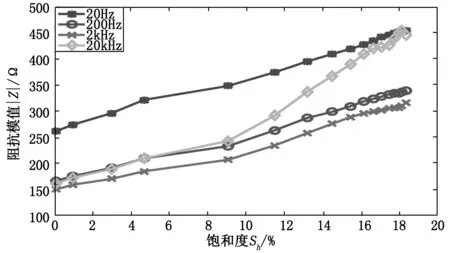
图4 特征频率点下阻抗模值随水合物饱和度的变化图
2.3.2 划分样本集
为了得到高效的神经网络模型,使之能够有效地逼近训练样本所蕴含的内在规律,需要将数据集划分为训练集和测试集。本文采用2/3的样本作为训练样本来训练网络,1/3的样本作为测试样本来测试网络,采用等间隔的方式从总样本集中取出。
3 水合物饱和度软测量模型
3.1 软测量模型设计
本文基于BP神经网络建立水合物饱和度软测量模型。设计步骤如下:1)确定BP子神经网络最优隐含层节点数,进而确定最优网络结构和训练参数;2)训练并测试子神经网络,根据多种误差指标评价网络性能;3)采用平均法集成策略,建立集成BP神经网络的水合物饱和度软测量模型。
3.2 BP网络结构和训练参数
神经网络理论证明,一个三层结构的BP网络可实现任意m维到n维的映射,并且通过调整隐含层神经元的个数来调节网络的精度[21]。因此,本文选用三层BP神经网络。网络的输入为一组传感器对在不同测试频率下的阻抗模值,输出为水合物饱和度。隐含层节点数的确定过程中参考式(3):
(3)
式中,L为隐含层节点数,n为输入层节点数,m为输出层节点数,a为1~10内的常数。
在分析评价网络的性能时采用以下4种误差指标[22]:相对误差(RE)反映测量结果偏离真值的实际大小;平均相对误差(MRE)反映误差的相对值,效果直观;平均绝对误差(MAE)反映预测值误差的实际情况;均方根误差(RMSE)反映网络预测值相对于实际值的平均离散程度。通过分析比较以上误差,可以确定更加合理地隐含层节点数。
在网络训练时,本文中隐含层的激活函数采用正切Sigmoid函数(tansig),其输入值可取任意值,输出值在-1~+1之间;输出层的激活函数采用线性函数(purelin),其输入值与输出值可取任意值;网络学习方法采用动量梯度下降法(traingdm),该方法不但具有较高收敛速度,而且通过引入一个动量项可以避免局部极小问题。
以上层1-5传感器对为例(参见图2),将隐含层节点数L取值由4增加到13,分别对不同隐含层节点数的网络进行500次训练和测试,通过分析比较网络误差来获得最优隐含层节点数。表1所示为500次测试误差的平均结果,各种误差指标的整体趋势为先减小后增大,普遍存在一个最小值。当L=9时,平均相对误差和均方根误差两项指标达到最优值,虽然没有实现全部指标都达到最优值,但此时指标取值与最优值相差较小。综合考虑,隐含层节点数设为9,从而获得针对上层1-5传感器对的水合物饱和度计算模型。采用同样的方法,根据表2、表3和表4的网络测试误差来确定针对2-6、3-7、4-8等传感器对的网络模型最优隐含层节点数,分别为9、10和10。
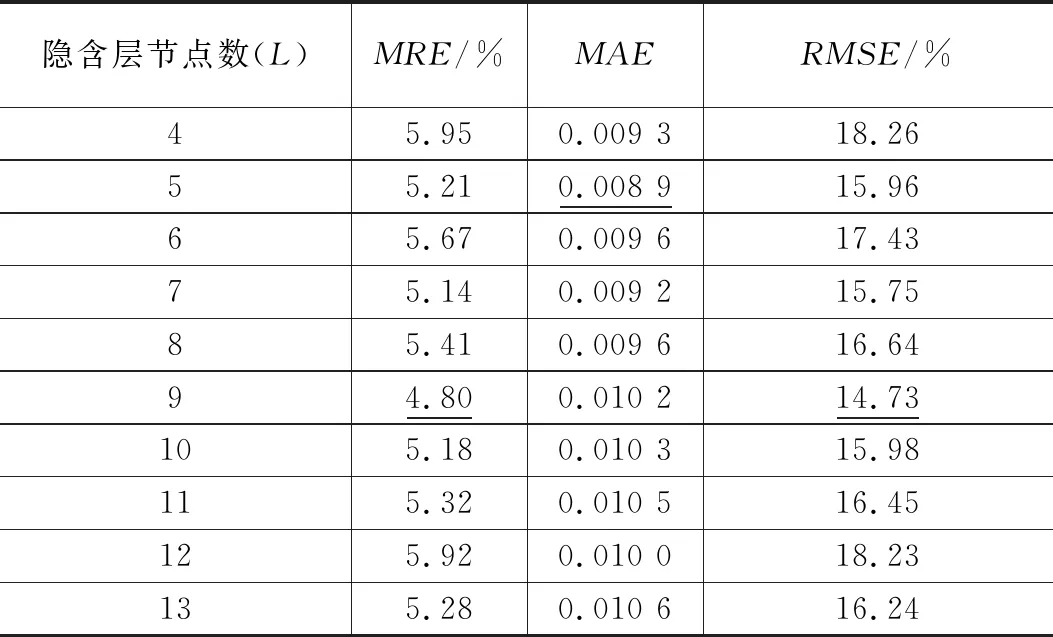
表1 上层1-5传感器对不同隐含层节点数网络测试误差表
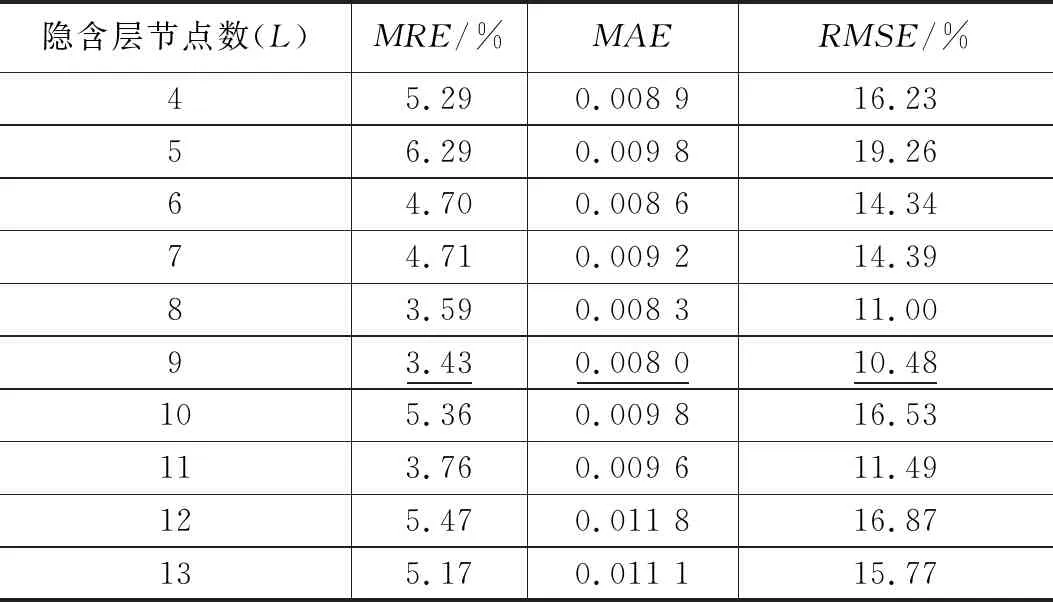
表2 上层2-6传感器对不同隐含层节点数网络测试误差表
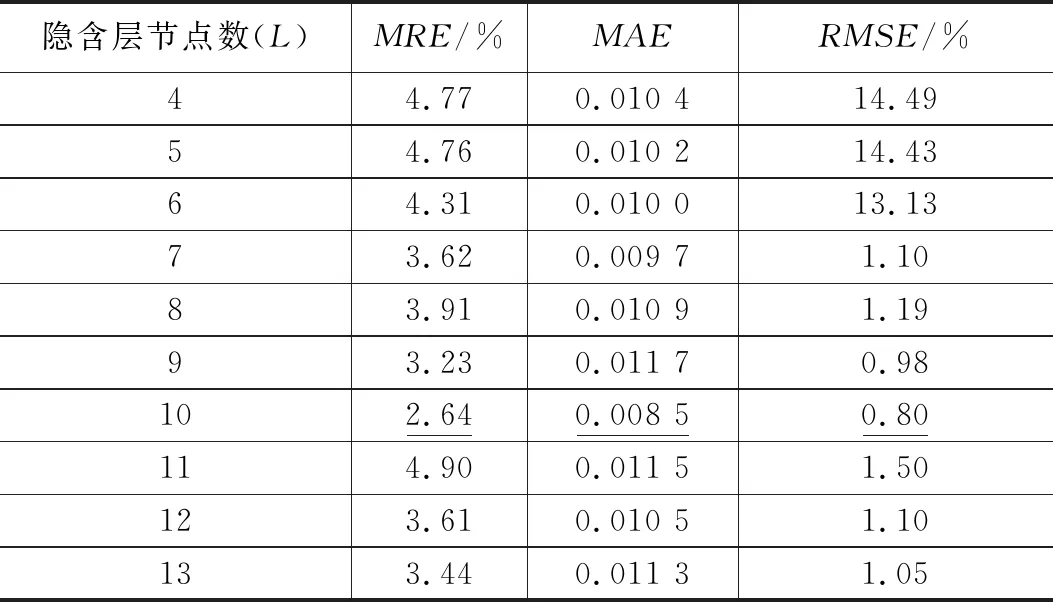
表3 上层3-7传感器对不同隐含层节点数网络测试误差表
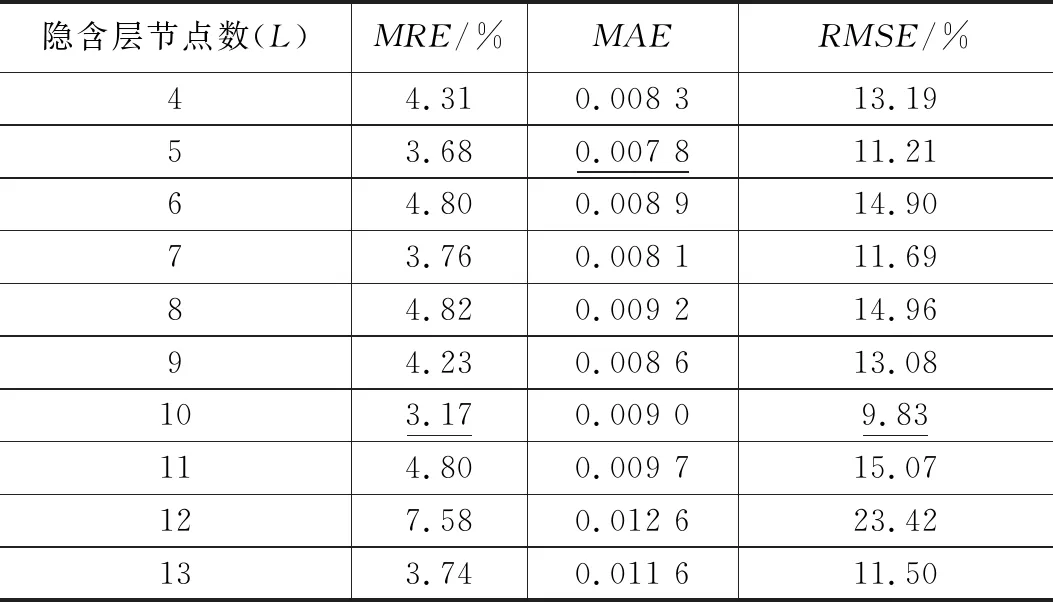
表4 上层4-8传感器对不同隐含层节点数网络测试误差表
3.3 测试和评价网络
将训练样本和测试样本分别输入上文所建立的具有最优结构和最佳性能的4个网络模型,进行训练和测试后得到如5所示的测试结果,误差统计列于表5。4个网络模型的平均相对误差|RE|<6%,平均绝对误差MAE<0.004,均方根误差RMSE<13%。
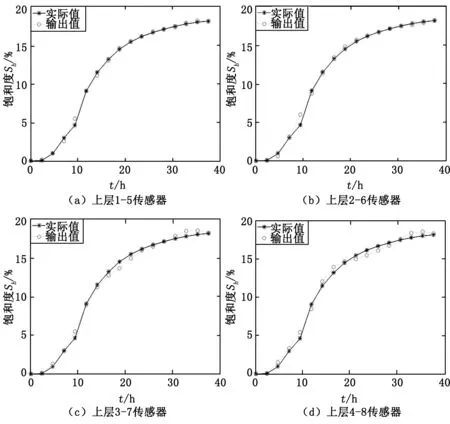
图5 4个子网络模型的输出值与实际值比较
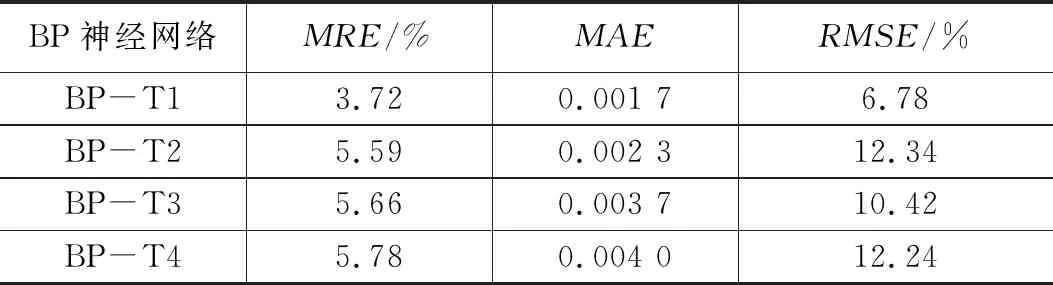
表5 各个子网络测试误差统计
3.4 集成网络模型设计
集成学习是指使用多个学习器对同一个问题进行学习,再使用某种策略将各个学习器进行集合,从而获得更优学习效果的机器学习方法。本文将以上所建立的4个子网络进行集成,以期获得性能更优的软测量模型。
当集成神经网络用于回归估计时,集成的输出通常由各网络的输出通过简单平均或者加权平均产生[25],即对各个学习器的输出结果求平均值,进而得到最终的预测结果,但是由于采用加权平均可能会导致过度拟合,从而使集成网络模型的泛化能力降低,因此本文选用简单平均法作为集成策略。图6中,ZTi表示通过不同传感器对测量得到的阻抗模值,BP-Ti表示对应不同传感器对的子网络。
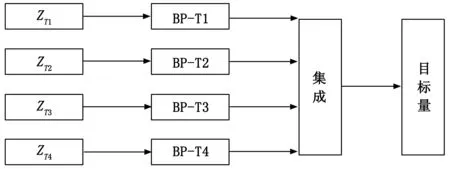
图6 集成网络模型结构示意图
图7和图8所示为集成网络模型的测试结果。与独立的子网络相比(表5所示),利用集成网络模型对饱和度进行预测时误差更小。集成神经网络的平均相对误差MRE为3.33%、平均绝对误差MAE为0.001 4、均方根误差RMSE为6.56%,三项误差指标均低于各个子网络的预测误差。集成神经网络的输入包含了通过4对传感器(位于4个测量方位)所获得的阻抗值,更多的信息量以及有效的集成策略对于提升预测模型的预测准确度提供了前提。
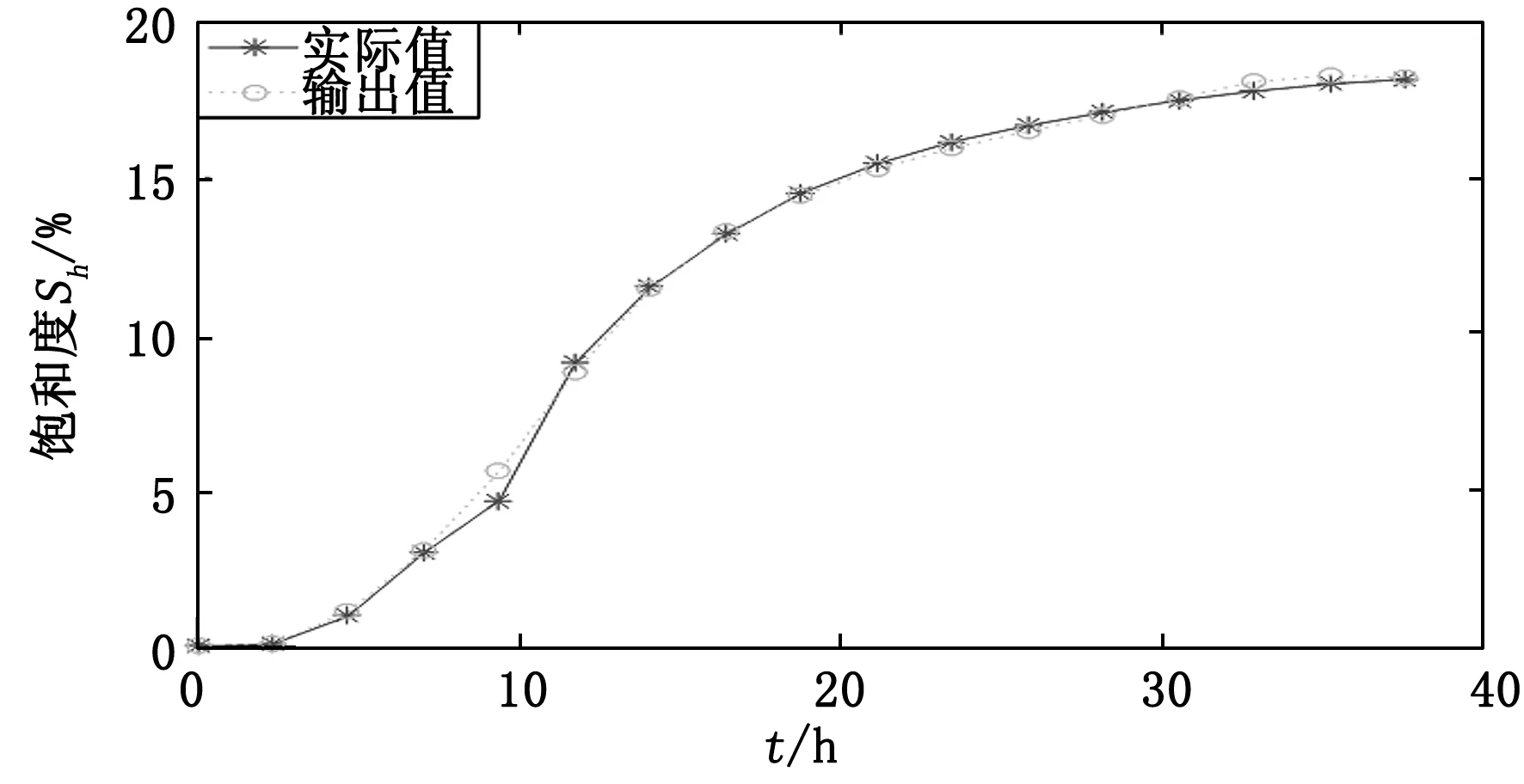
图7 集成网络模型预测输出
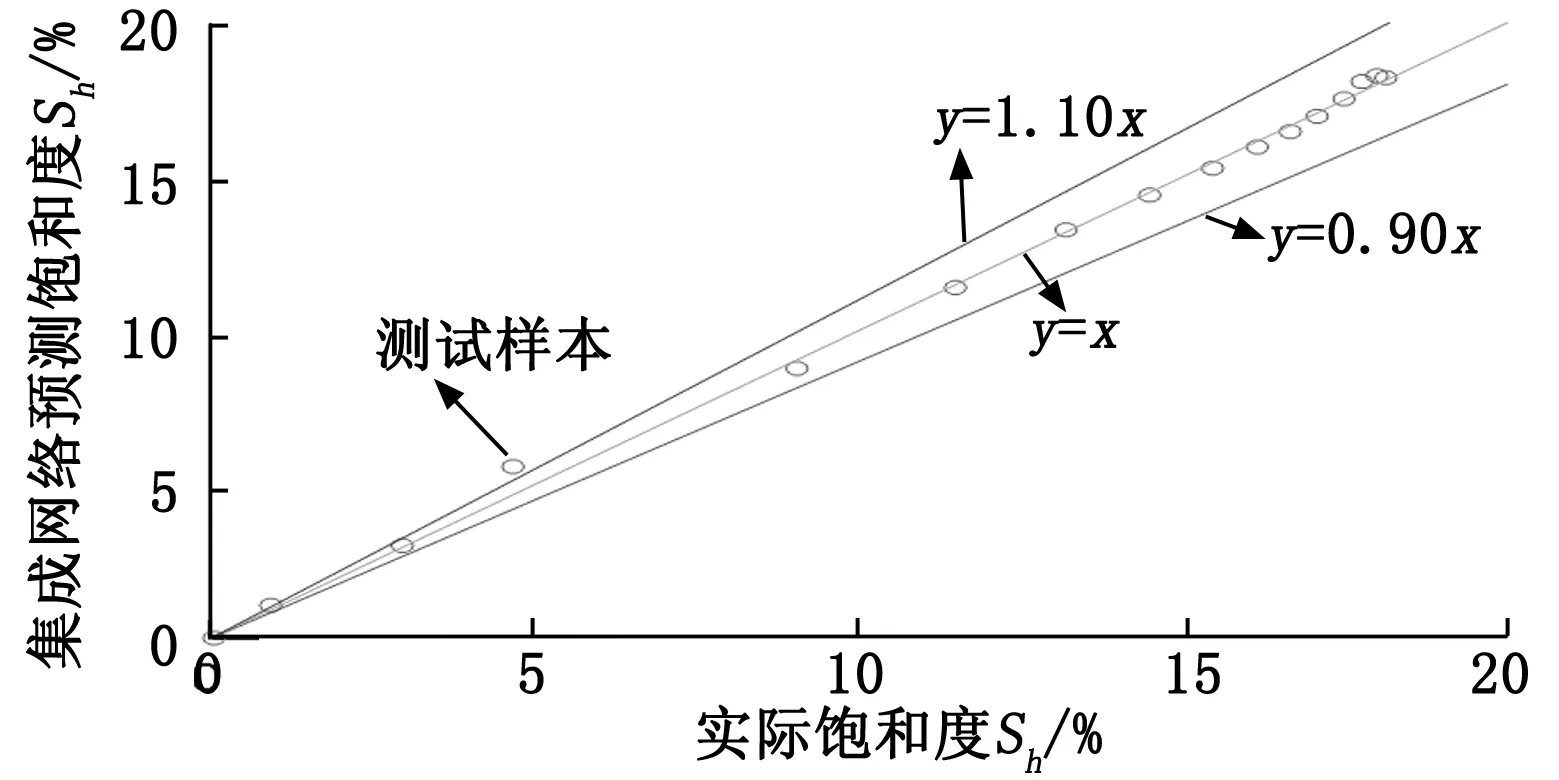
图8 集成网络预测值相对误差
4 结束语
针对沉积物中含天然气水合物饱和度的计算问题,提出了一种基于电阻抗特性参数和集成神经网络的软测量模型建立方法。开展了甲烷水合物模拟实验并获取了电阻抗谱、温度和压力数据,在对电阻抗谱数据进行预处理、特征参数提取和选择之后形成了样本集,针对4对传感器分别设计了BP神经网络,继而将4个BP网络作为子网络进行集成得到集成网络模型。模型测试结果表明:通过集成网络模型计算得到的含水合物饱和度值平均相对误差3.33%、平均绝对误差0.001 4、均方根误差为6.56%,三项误差指标均低于各个子网络的计算误差。
通过在宽频范围内对含水合物沉积物进行电阻抗谱测试,能够获得沉积物的频率响应特性以及特性描述参数(如不同频率条件下的阻抗模值),从而能够为神经网络模型提供大量的输入信息。利用集成神经网络能够综合应用位于不同测量方位的多个传感器的测量数据,通过采用适合的集成策略能够克服水合物空间分布不均匀对饱和度计算准确度的不利影响。
基于集成神经网络的软测量模型能够接受多维度、丰富的输入信息,非常适合于解决复杂沉积物中含水合物饱和度的评价问题,下一步将在扩大饱和度范围的基础上,联合应用声学特征参数和电学特征参数作为模型的输入,以期获得更加可靠、精确的饱和度评价结果。
