基于灰色神经网络的装备计量预测研究与实现
2020-06-29周东方1王志虎丁风海
周东方1,,王志虎,丁风海
(1.国防科技大学 计算机学院,长沙 410073; 2.中国卫星海上测控部 技术部,江苏 江阴 214431)
0 引言
计量是保证测量实现单位统一和量值准确可靠的一门科学[1],装备保障机构在对装备实施量值传递或量值溯源的过程中,保存着装备周期校准/检定数据,如何使其运用于基于数据驱动的装备状态预测[2]中,并更好地服务于装备维护保障,成为装备保障人员需要面对的问题。
对于样本数据不大的装备状态预测,前人提出了将适于小样本、贫信息的灰色理论[3-6]和具有较强非线性映射能力的神经网络[7]相结合的灰色神经网络理论[8]。目前,常见组合方式有并联型、串联型和嵌入型等[8-11],但上述组合模型中仍需要一定数量的样本数据对神经网络进行训练,考虑到装备历史计量数据样本较少(装备周期溯源一般一年一次)、健康状态信息不全等特点,为避免较少学习样本导致的训练后神经网络较差的泛化能力,本文基于灰色神经网络理论中用神经网络增强灰色系统的方法,并提出一种基于RBF神经网络优化GM(1,1)模型的组合模型。实例分析结果表明,该模型提高了GM(1,1) 传统模型精度,适用于基于计量数据的装备技术状态预测。
1 灰色神经网络模型
1.1 GM(1,1)传统模型
灰色系统理论中,用离散数据列建立的微分方程型动态模型,称为灰色模型(GM,grey model),其中只有一个变量且为一阶的灰微分方程模型称为GM(1,1)模型[3],它是最常用的一种灰色模型,其4个数据即可建模是其他模型不可比拟的优势,被广泛应用于多个领域[3-6]。GM(1,1)模型通过累加、累减处理,增强数据的规律性,弱化随机性,然后利用处理后的离散数据列建立微分方程的动态模型,从而得到原始数据较为本质的特性,具体过程如下:
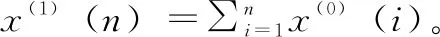
x(1)数列紧邻均值等权生成白化背景值数列z(1)为:z(1)={z(1)(2),z(1)(3),…,z(1)(n)},式中:z(1)(k)=0.5(x(1)(k-1)+x(1)(k)),k=2,3,…,n。
则灰色模型GM(1,1)灰微分方程的基本形式为:
x(0)(k)+az(1)(k)=b
(1)
式中,a为发展系数,b为会作用量。
其白化方程为:
dx(1)/dt+ax(1)=b
(2)
(3)
则GM(1,1)白化方程的解为:
(4)
累减还原值为:
(1-ea)(x(0)(1)-b/a)e-ak,k=1,2,…,n
(5)
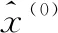
1.2 RBF神经网络
径向基(radical basis function,RBF)神经网络[7]是一种高效的前馈式神经网络,其结构简单、训练速度快,具有最佳的逼近性能和全局最优特性,广泛应用在非线性函数逼近、模式识别等领域。
(6)
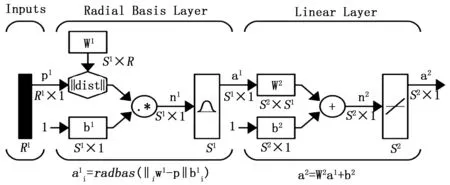
图1 RBF神经网络结构
第三层为输出层(线性层),它对输入模式做出响应,即网络输出为:
a2=purelin(n2)
(7)
其基本思想即用RBF作为隐节点的“基”构成隐含层空间,隐含层对输入矢量进行变换,将低维的模式输入数据变换到高维空间内,使得在低维空间内的线性不可分的问题在高维空间内线性可分,相当于在一个隐含的高维空间中找到最佳拟合的训练数据表面。
根据径向基函数中心确定方法的不同,RBF神经网络有不同的学习策略,常见的有随机选取固定中心、自组织选取中心、有监督选取中心、正交最小二乘法等方法。当采用正则化RBF网络结构时,隐节点数即样本数,基函数的中心即为样本本身。
1.3 GM(1,1)优化模型
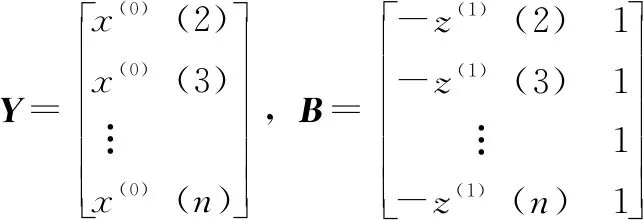
GM(1,1) 传统模型的固有缺陷主要是指白化方程与灰微分方程的不匹配问题及初始条件的选择问题[12-13]。相对而言,初始条件对拟合精度的影响一般不及前者,其改进方法也多是添加一个初始值修正项或以最小二乘原理求解最优初值,其中针对白化方程与灰微分方程的不匹配问题,可以采用多种修正方法,主要为背景值构造的改进、白化方程参数重构、灰微分方程建模以及直接求解参数法等[13]。其中背景值构造的改进是最常见的GM(1,1)模型改进方法,由GM(1,1) 传统模型的建立过程可知,原始数据数列一次累加生成序列x(1)具有灰指数率,GM(1,1)模型模拟和预测精度取决于参数a和b,而参数a和b的值又依赖于原始数据数列和背景值,因此背景值构造公式是否合理直接影响模型的模拟和预测精度。
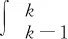
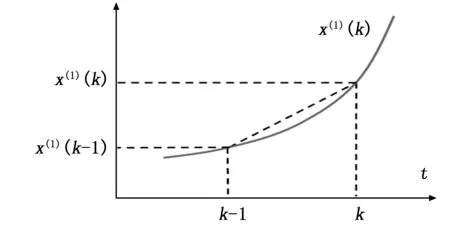
图2 GM(1,1)背景值计算
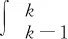
文中GM(1,1)模型背景值优化在Matlab环境下编程实现,正则化RBF神经网络由newrb()函数建立[14],其调用格式为net=newrbe(P,T,SPREAD),其中P为Q组输入向量组成的R*Q维矩阵,T为Q组目标分类向量组成的S*Q维矩阵,SPREAD为径向基函数的扩散速度(式(6)中b1=0.8326/SPREAD),默认值为1。如图3所示,基于RBF神经网络的GM(1,1)模型背景值优化方法构建过程如下:
步骤1:输入原始数据x(0),得到其一次累加生成数据序列x(1)。
步骤2:在一定范围内步进调整设置不同SPREAD值,以数列x(1)中各元素序列号和值,分别作为RBF神经网络的输入和输出训练样本,对其进行训练,得到数列x(1)的拟合曲线。
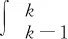
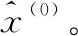
步骤5:对GM(1,1)模型进行残差检验[3-4],计算序列中实际数据与其拟合值的平均相对残差:
(k)|
(8)
式中,
(9)
步骤6:以最优SPREAD值下,步骤4得到的结果作为建模结果。
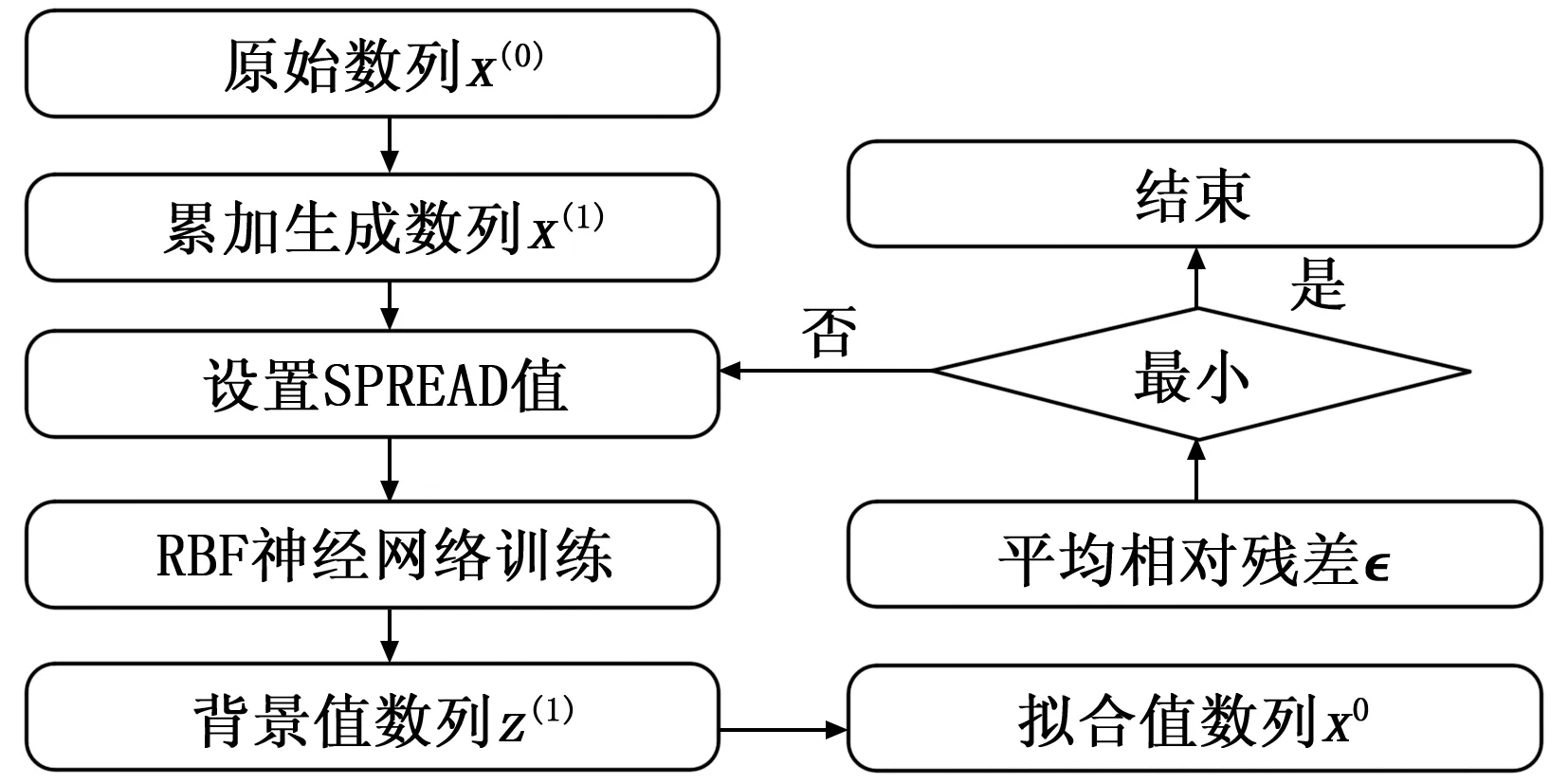
图3 GM(1,1)模型背景值优化过程
2 基于灰色神经网络模型的实例分析
文中选择直流电压标准732B输出端10 V及1.018 V历年校准数据(如表1所示)为实例进行分析。
基于上述表格中2018年前不同长度的历史数据,分别预测10 V及1.018 V输出端2018年及2019年的校准值。

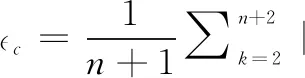
c(k)| (10)
10V端不同历史数据长度GM(1,1)传统模型和优化模型预测数据分别如表2和表3所示。
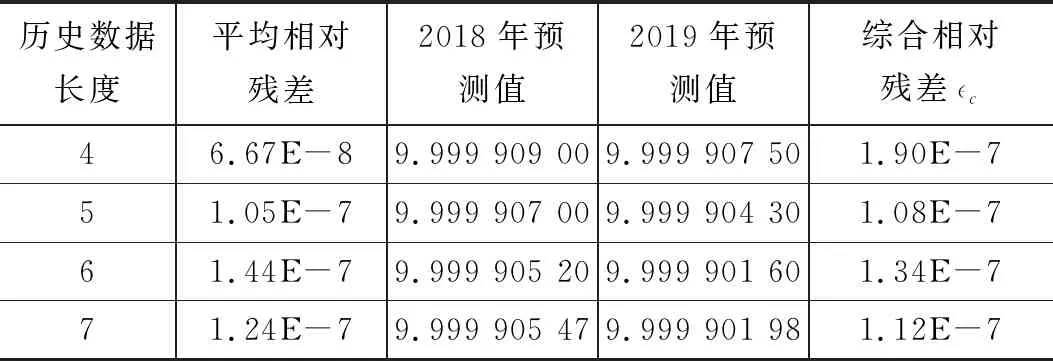
表2 10 V端不同历史数据长度GM(1,1)传统模型预测
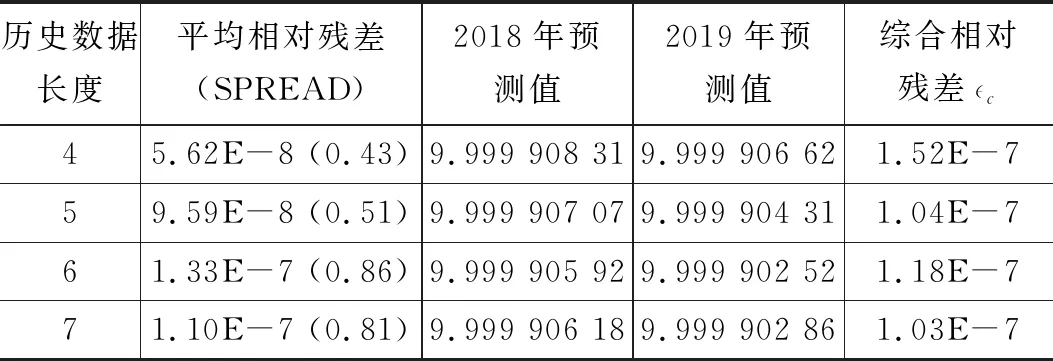
表3 10 V端不同历史数据长度GM(1,1)优化模型预测
图4为10 V端GM(1,1)不同模型相对残差趋势图,可以看到,不同历史数据长度下,GM(1,1)优化模型的平均相对残差和综合相对残差均小于传统模型。
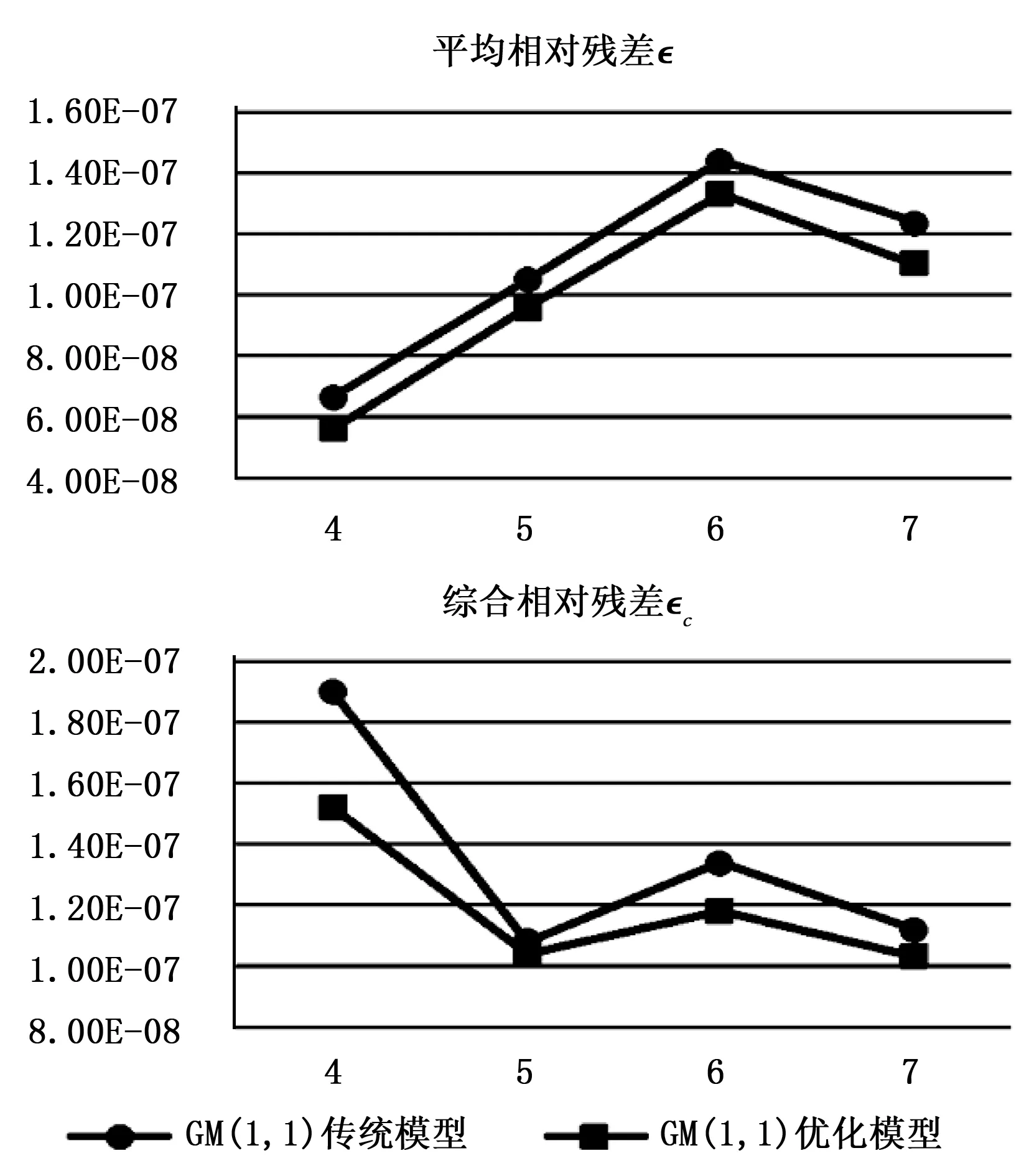
图4 10 V端GM(1,1)不同模型相对残差趋势
1.018 V端不同历史数据长度GM(1,1)传统模型和优化模型预测数据如表4和表5所示。
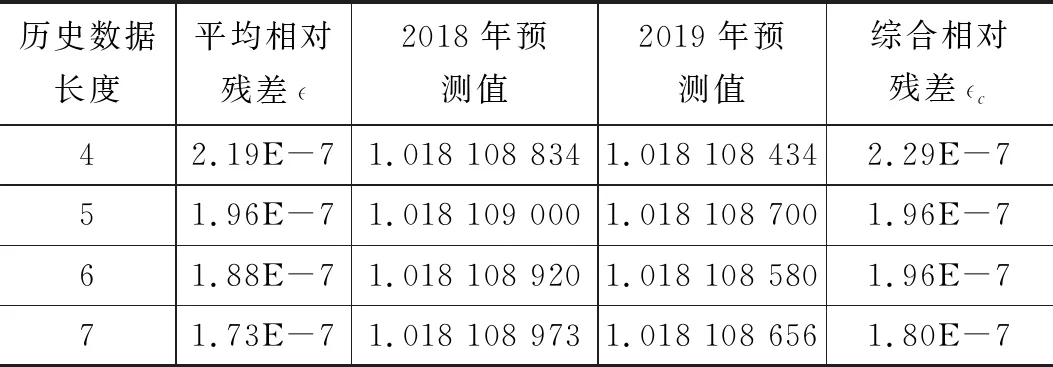
表4 1.018 V端不同历史数据长度GM(1,1)传统模型预测
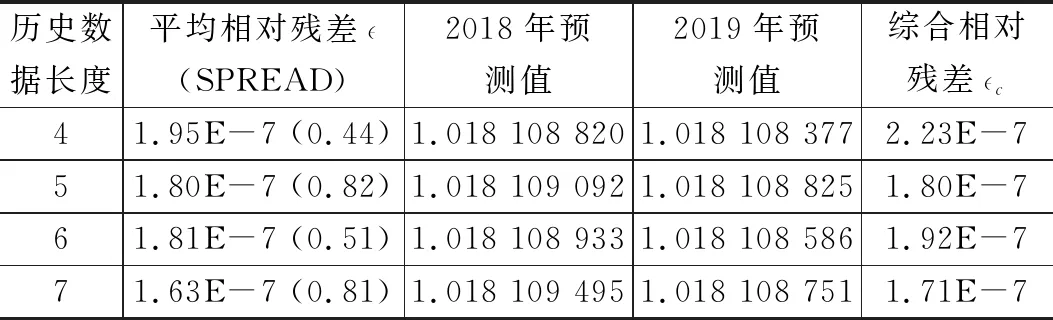
表5 1.018 V端不同历史数据长度GM(1,1)优化模型预测
图5为1.018 V端GM(1,1)不同模型相对残差趋势图,可以看到,不同历史数据长度下,GM(1,1)优化模型的平均相对残差和综合相对残差同样均小于传统模型。
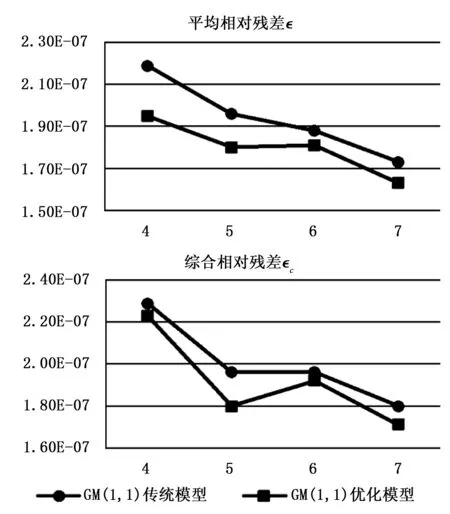
图5 1.018 V端GM(1,1)不同模型相对残差趋势
直流电压标准732B技术说明书中,10 V端的年稳定度为2.0×10-6,由上述数据分析可以看到,10 V端2018年和2019年预测值与实际校准值相对残差均小于2.0×10-6且小了一个量级,即上述两种GM(1,1)模型均可以给出合理的预测值。
3 装备计量预测软件实现
由于Matlab具有良好的神经网络设计及实现能力,根据前述GM(1,1)传统模型和GM(1,1)优化模型,基于Matlab提供的专用图形用户界面设计工具GUIDE(graphical user interface development environment)开发装备计量预测软件,用于实现装备计量状态在不同GM(1,1)模型下的预测及比较。
GUIDE主要包含一个界面设计工具集,且Matlab集中了所有GUI(graphical user interface)支持的用户控件,并且提供了界面外观、属性和行为响应方法的设置方法,其开发环境类似于VB、VC的开发环境,直接将所需的对象拖拽到目的位置,即可完成GUI布局设计,相关对象的响应功能需编辑其M文件存储的对应回调函数。
装备计量预测软件的软件流程如图6所示。软件经初始化,输入历年装备计量数据及年份,同时程序自动显示并绘制上述数据;输入数据后,数据可分别选择GM(1,1)传统模型及优化模型对上述数据进行预测,同时程序添加显示并绘制上述预测数据。
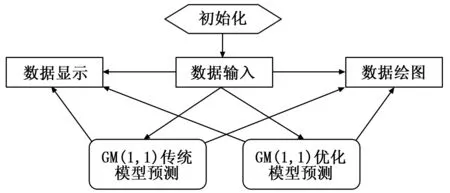
图6 装备计量预测软件流程图
装备计量预测软件主界面如图7所示,界面较为简洁,且便于使用。主界面主要包括3个部分:数据单元、预测单元及绘图单元。
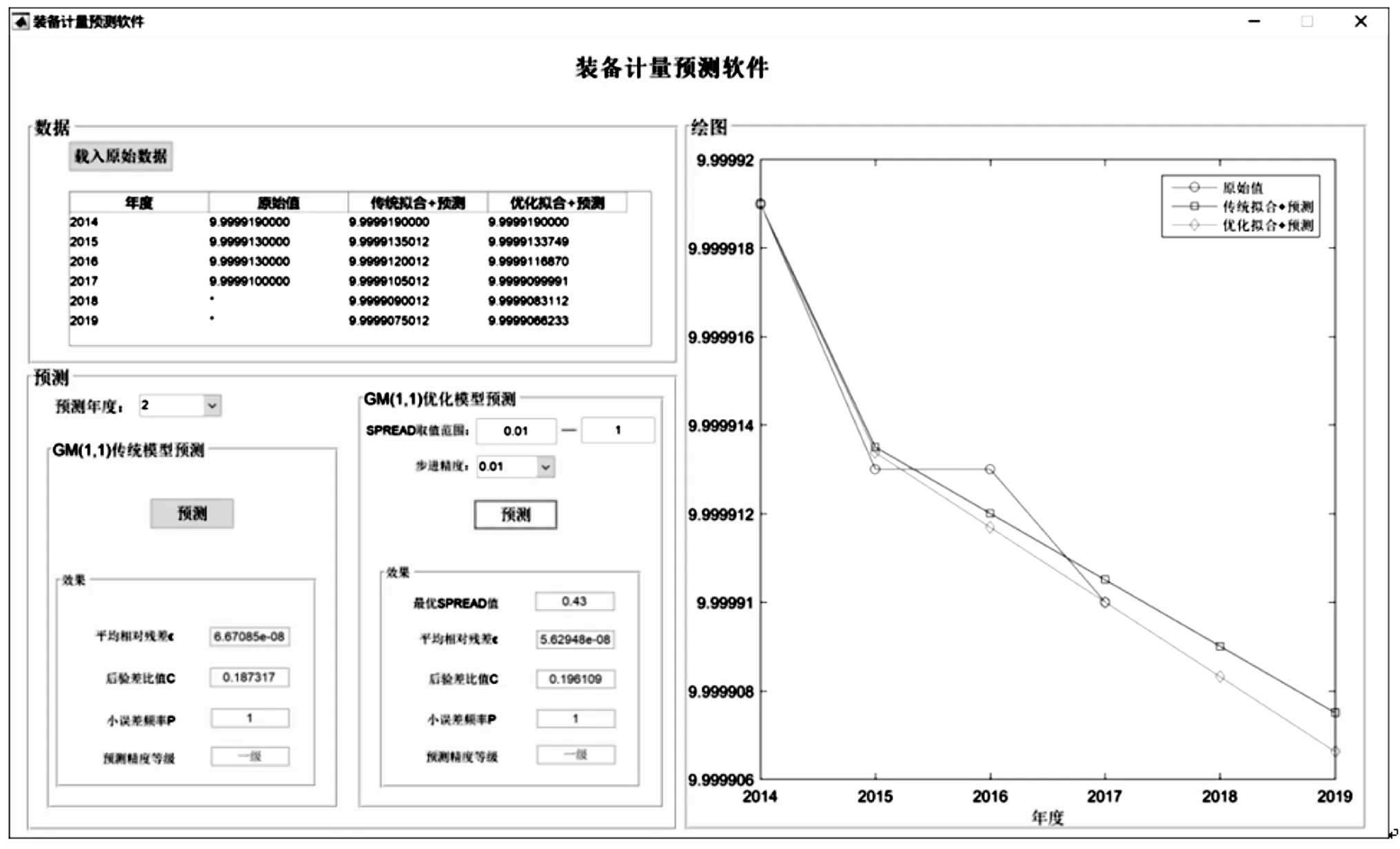
图7 装备计量预测软件界面
其中数据单元主要包括原始数据的载入及相关数据的显示。该单元通过“载入原始数据”按钮载入以txt文本文档形式存储的原始数据,并显示在按钮下面的表格中,且该表格同时会根据预测过程增加显示相关预测数据。
预测单元包括基于GM(1,1)传统模型和GM(1,1)优化模型的两种预测方式,其中预测年度只提供了1年或2年的选项,这是因为装备计量一般一年一次,较长时间跨度的预测并无多少意义。GM(1,1)优化模型预测中,需首先对GM(1,1)背景值优化的RBF神经网络SPREAD取值范围(如0.01~2)及步进调整大小(程序中提供了0.01和0.1两个选项)进行设定,然后程序按照1.3节中基于RBF神经网络的GM(1,1)模型背景值优化方法构建过程对SPREAD值寻优,并以此值下得到的拟合值序列为最终结果,当然在上述范围内未得到合适的结果时,可修改SPREAD取值范围并重新寻优,直至找到合适的结果。同时预测单元根据不同模型的预测,对上述模型拟合结果进行残差检验(平均相对残差)和后验差比值(后验差比值、小误差频率及判断预测精度等级)[3-4]检验。
绘图单元主要通过对数据单元表格中数据的图形展示,便于用户更为直观地了解和观察预测结果,通过原始数据及拟合预测数值的曲线图,在整体上了解预测效果。
4 结束语
本文考虑到少量装备计量数据的情况下,将适合小样本、贫信息的灰色GM(1,1)模型用于装备计量预测,同时为提高GM(1,1)传统模型精度,利用RBF神经网络良好的函数拟合特性优化GM(1,1)背景值构造过程,从而得到组合形式的GM(1,1)优化模型,并通过对直流电压标准732B历年计量数据进行实例分析,验证该GM(1,1)优化模型在较少计量数据情况下具有良好的预测性能,且模型精度优于GM(1,1) 传统模型,同时基于Matlab
开发的装备计量预测软件,提供了上述两种模型的预测比较,相关预测程序可应用于装备计量测试软件及过程中,为实现基于计量数据的装备技术状态预测提供了技术手段。
