九年级数学复习课中培养学生数学核心素养的教学实践

任健

摘 要：数学中对核心素养内容的应用包括在代数、几何和统计方面的具体知识，在研究上述内容时所使用的方法和由此提升的能力都融入到核心素养中，在与社会生活产生联系的同时，加深数学理论对于实践生活的指导作用。初中数学的复习过程，需要教师对知识间内在的联系以框图或者图表的形式呈现出来，给学生整体性的感受，对每个复习的环节理清所需的技能方法，在深挖数学实质的基础上，增添科学素养的内容。本文将以二次函数的复习为例，浅谈在数学复习课中核心素养的渗透方式。

关键词：九年级数学;复习;核心素养

引言：

复习课的作用是巩固原有知识，对七八年级没能完全掌握的内容加以深化，由知识水平的提升过渡到能力的提升层面，引导学生在消除知识桎梏的同时，渗透进核心素养。复习教学活动的开展，要立足于中考的考点和需要掌握的典型例题，明确每个题型涉及的数学思想，使用的数学方法，判定其属于哪个基本模型，以整体眼光审视数学问题，从中获取规律性的解决办法。

一、以“二次函数”复习为例的必要性

二次函数的内容是中考的必考题型，涵盖的知识点较多，可与其他函数知识点结合成为一道综合性大题，通过多年的教学经验发现，学生对于二次函数的掌握程度制约着分数的高低。“数形结合”的思想在二次函数的解题过程中体现的淋漓尽致，学生通过给定的文字内容，画出符合题意的图像，结合已有知识内容，分析题意，选用适当的解题技巧，从思维上构建起性质与应用的桥梁，达到准确解答的效果[1]。

二、教学过程

教学活动 学生做法 教学目的

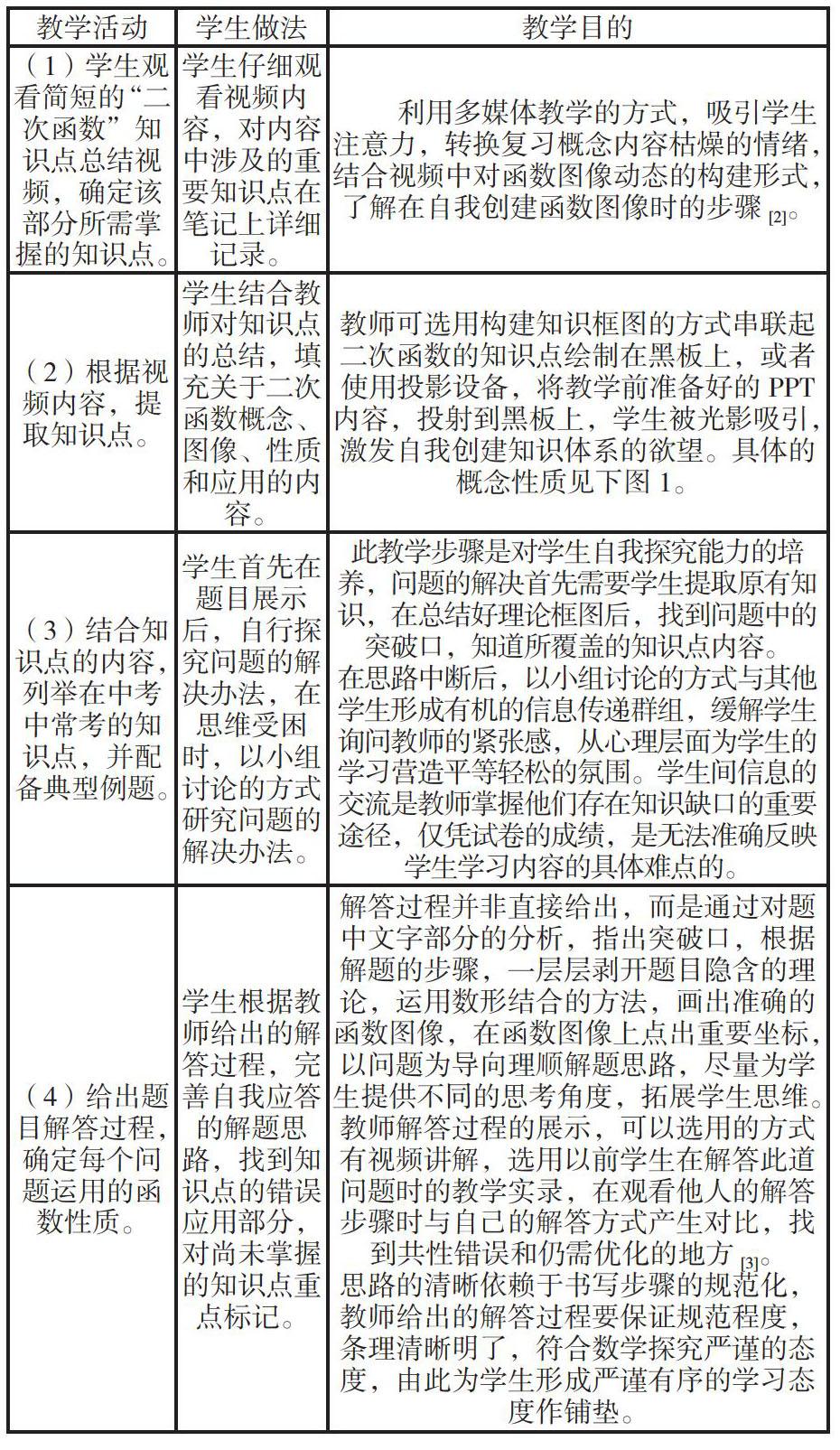
（1）学生观看简短的“二次函数”知识点总结视频，确定该部分所需掌握的知识点。 学生仔细观看视频内容，对内容中涉及的重要知识点在笔记上详细记录。 利用多媒体教学的方式，吸引学生注意力，转换复习概念内容枯燥的情绪，结合视频中对函数图像动态的构建形式，了解在自我创建函数图像时的步骤[2]。

（2）根据视频内容，提取知识点。 学生结合教师对知识点的总结，填充关于二次函数概念、图像、性质和应用的内容。 教师可选用构建知识框图的方式串联起二次函数的知识点绘制在黑板上，或者使用投影设备，将教学前准备好的PPT内容，投射到黑板上，学生被光影吸引，激发自我创建知识体系的欲望。具体的概念性质见下图1。

（3）结合知识点的内容，列举在中考中常考的知识点，并配备典型例题。 学生首先在题目展示后，自行探究问题的解决办法，在思维受困时，以小组讨论的方式研究问题的解决办法。 此教学步骤是对学生自我探究能力的培养，问题的解决首先需要学生提取原有知识，在总结好理论框图后，找到问题中的突破口，知道所覆盖的知识点内容。

在思路中断后，以小组讨论的方式与其他学生形成有机的信息传递群组，缓解学生询问教师的紧张感，从心理层面为学生的学习营造平等轻松的氛围。学生间信息的交流是教师掌握他们存在知识缺口的重要途径，仅凭试卷的成绩，是无法准确反映学生学习内容的具体难点的。

（4）给出题目解答过程，确定每个问题运用的函数性质。 学生根据教师给出的解答过程，完善自我应答的解题思路，找到知识点的错误应用部分，对尚未掌握的知识点重点标记。 解答过程并非直接给出，而是通过对题中文字部分的分析，指出突破口，根据解题的步骤，一层层剥开题目隐含的理论，运用数形结合的方法，画出准确的函数图像，在函数图像上点出重要坐标，以问题为导向理顺解题思路，尽量为学生提供不同的思考角度，拓展学生思维。教师解答过程的展示，可以选用的方式有视频讲解，选用以前学生在解答此道问题时的教学实录，在观看他人的解答步骤时与自己的解答方式产生对比，找到共性错误和仍需优化的地方[3]。

思路的清晰依赖于书写步骤的规范化，教师给出的解答过程要保证规范程度，条理清晰明了，符合数学探究严谨的态度，由此为学生形成严谨有序的学习态度作铺垫。

（5）课堂反思：询问学生在本节课的学习中有哪些收获？对二次函数的有关问题还存在哪些尚未解决的难题？在全班范围内讨论。 学生回答：对二次函数概念和图像有了进一步的认识，基本了解中考中关于二次函数问题的出题方向，明确“数形结合”思想在有关函数问题中的指导性作用，确定解答二次函数大题的书写步骤。对于二次函数最值、增减性和与图形的结合问题仍需要加强练习。 教师及时在课堂的结尾引导学生自我反思，整理本节课程复习的内容，在学生谈及积极的收获中给予肯定，对他们抽象和概括能力的提升起到积极的促进作用。

结束语

综上所述，复习是教师重点渗透核心素养的阶段，在此阶段能够对学生的概括总结、抽象模型能力加深培养力度，帮助他们以知识框架的形式烙印下中学数学的理论联系。教师在制定复习计划过程中，应当充分把控学生的发展现状，有针对性的开展教学活动。

参考文献

[1]冯晓音.思维导图在初中数学复习课中应用的研究[D].陕西师范大学，2019.

[2]穆道龙.浅析初中数学复习课教学的有效策略[J].中国校外教育，2018，36：116.

[3]杨丹.基于案例分析的初中数学復习课问题研究[J].科学咨询（教育科研），2019，03：74.