刘徽《九章算术注》中的数学思想方法及其贡献

吴维煊, 章秋香

(宿迁经贸高等职业技术学校， 江苏 宿迁 223600)

0 引言

刘徽生活在三国时代的魏国，他从事过野外测量，研究过天文历法，但他最主要的工作是数学研究. 他自幼攻读《九章算术》，在攻读的过程中发现很多问题的表达方式不佳，问题的解决方式较为零散，缺乏系统性，于是开始为《九章算术》全书做注释,成书《九章算术注》. 刘徽在《九章算术注》中处处闪烁着先进数学思想的光辉，不仅让中国古代数学体系趋于系统化，而且为完善古算理论做出了突出贡献. 目前，关于刘徽《九章算术注》的研究论文较多，主要涉及某一思想方法的研究，如科学思想的来源[1]、形象思维中的几何理论[2]及演绎逻辑思维[3]等方面,系统研究刘徽的数学思想方法，特别是刘徽的辩证法思维，在现有文献中尚未见到. 本文深入探索刘徽《九章算术注》中的辩证法、复杂问题转化、逻辑推理、敢于创新等思想方法及其贡献。

1 《九章算术注》中的数学思想方法

1.1 朴素的辩证法思想

刘徽在为《九章算术》做注释过程中，遵循朴素的辩证法思想，突破了《九章算术》一题一解的局限性，主张具体问题具体分析，解决数学问题不应拘于一法，应思考多种解决问题的方法，及各种方法中的联系. 在多种解法中，到底用哪个方法，刘徽认为“可随率宜也”，用现代人的说法，就是“要辩证地看问题”.

例如 《九章算术》“方程”章最后一题，“今有麻九斗、麦七斗、菽三斗、荅二斗、黍五斗，直钱一百四十；麻七斗、麦六斗、菽四斗、荅五斗、黍三斗，直钱一百二十八；麻三斗、麦五斗、菽七斗、荅六斗、黍四斗，直钱一百一十六；麻二斗、麦五斗、菽三斗、荅九斗、黍四斗，直钱一百一十二；麻一斗、麦三斗、菽二斗、荅八斗、黍五斗，直钱九十五，问一斗值几何”.

该问题的解决相当于解下面的五元线性方程组:

求解这个方程组比较麻烦，刘徽写了一篇叫《方程新术》的文章，文章中提出了3种解法.

解法1该解法的中心思想是消去常数项，然后再把每行(方程)的项数减到只剩两项，最后再用比例表示5个未知数之间的关系. 求出一个未知数的解之后，其余未知数也可求出. 在求解的过程中，刘徽有一段精彩的叙述：“令左右相减，先去下实，又转去物位，求其一行二物正负相借者，易其相当之率. 又令二物与他行互相去取，转其二物相借之数，即皆相当之率也……”他用此法求得5个未知数中任意两个未知数之间两两“相当之率”[4]：

4x=7y、3y=4z、5z=3u、6u=5v.

如何由这个比例式求解5个未知数？由(3)-(4)得

x+4z-3u=4.

(6)

解法2该解法的中心思想是由各式连续减式(6)，消去首项. 因为式(6)首项系数为1，可以不必互乘. 利用这种方法，先求出未知数u=6，再依次求出其余4个未知数.

解法3该解法的中心思想是运用连比例这一方式，刘徽将这种解法概括为“置群物通率为列衰，更置减行群物之数，各依其率乘之，并以为法”. “群物通率”就是根据解法1中的比例有

x∶y∶z∶u∶v=7∶4∶3∶5∶6，

再通过式(6)(“减行”)即可求得.

这3种解法虽然使用方法不同，但各种方法之间有一定的联系，各种方法的结果可以互用. 用何种方法解决这一问题，需要用辩证的思维，根据所要求解的问题及个人解决问题的习惯及方式，做到如刘徽所言“可随率宜也”. 刘徽朴素的辩证法思维，为后人学习数学、解决数学问题提供了很好的范本. 辩证法思想的应用，也是数学教学中具体问题具体分析的重要思想方法.

1.2 在不同的数学问题中挖掘一般规律

刘徽在《九章算术注》的序文中说“事类相推，各有攸归，故条枝虽分而同本榦者，知发其一端而已”. 这段描述的意思是有许多数学问题，表面上看问题表述方式各不相同，但在数学理论上却是一致的，他们是有共同根源的相同问题. 刘徽善于寻求不同数学问题内部的一般规律，如在“勾股”章16题注中说：“言虽异矣，及其所以成法，实则同归矣”[5].

“齐同术”理论的完善及推广，充分彰显了刘徽在不同数学问题中挖掘一般规律的数学思想. 刘徽把赵君卿关于“齐同”的定义进一步加以解释，在“衰分”章“返衰”下注称“母同则子齐，齐即衰也”，即：将一组分数通分后，根据分子的大小关系，就可得到分数间的大小关系.

刘徽进一步完善“齐同术”理论后，指出其他数学问题，诸如求几个分数的平均值、解释衰分术、均输、盈不足和方程等问题，都有“齐同术”的一般规律，因而“齐同术”是解决该类问题的方法之一. 在数学教学中，很多老师受刘徽思想方法的影响，很注重培养学生一题多变，在多种问题中探讨一般规律的思维.

1.3 用不同的方法解决相同问题

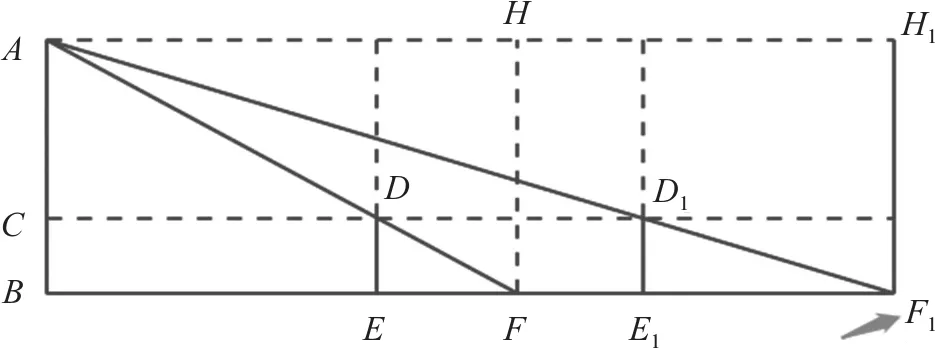
《海岛算经》第1题，今有望海岛(AB)，立两表(DE和D1E1)齐高三丈，前后相去(EE1)千步. 令后表与前表相直. 从前表(DE)却行123步，人目著地(F)取望岛峰(A)，与表末(D)参合，从后表(D1E1)却行(E1F1)127步，人目著地(F1)取望岛峰(A)，亦与表末(D1)参合，问岛高AB及去表(BE)各几何(图1)？

刘徽以“术”的形式给出了计算公式. 若用现代符号表示，该公式为

(7)

(8)

这一问题是对同一目标在不同地点两次立表进行测量，其解法是利用两次测量数据进行计算，所以叫“重差”. 式(7)～式(8)可由“出入相补”原理推出.

ACBHH1DD1EFE1F1

图1 望海岛示意图

如图1，D1是矩形AF1的对角线上的一点，所以，矩形D1H1的面积=矩形D1B的面积，即

AC·E1F1=BE1·DE.

(9)

又D是矩形AF的对角线上的一点，所以矩形DH的面积=矩形DB的面积,即

EF·AC=BE·DE.

(10)

(9)-(10) 得AC·(E1F1-EF)=DE·EE1，所以

(11)

式(11)的两边同加DE，即得公式(7).

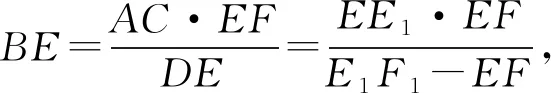
由此可见，刘徽《海岛算经》解测望问题的主要工具是“出入相补”原理，不涉及角和三角函数概念，这与西方的三角测量有明显的区别. 他还运用“类推衍化”的方法，使重差术由两次测望，发展为“三望”“四望”. 而印度在7世纪，欧洲在15～16世纪才开始研究两次测望的问题. 在数学教学中，一题多解是拓展数学思维、培养数学能力的重要学习方法，该方法在数学教学中的普遍应用，是刘徽在注释中为后人留下的宝贵财富.

1.4 将难以解决的复杂问题进行转化

刘徽将难以解决的复杂问题进行转化，对数学教学的影响是深远的. 当某一数学问题无法解决时，对问题进行转化，将一个问题分解成若干问题，将显性问题转化成隐性问题，将代数(或几何)问题转化成几何(或代数)问题，是求解数学问题的重要方法.

1.5 严谨的逻辑推理

刘徽对《九章算术》中的所有数学概念都做了解释或逻辑定义，在解释和定义中，他非常注意数学推理的逻辑性，充分考虑各问题之间的逻辑关系. 在“勾股”章的注释中，明确指出：这一章之所以一开头就提出了勾股定理，是因为“将以施于诸率，故先具此术，以见其源也”. 刘徽用这一精彩的论述，从“逻辑”角度注释了勾股定理出现在“勾股”章开头的必要性. 刘徽认为有些问题不能只限于感性认识，必须在感性认识的基础上提升到理性认识的层面，并在理性认识的基础上形成数学理论. 因而，他从逻辑严谨性出发，对于那些能从逻辑上证明的法则都进行了论证.

刘徽创造的十进小数，就是逻辑推理的最好实证. 在刘徽提出十进小数以前，计算中遇到奇零小数时，或是化为分数，或是用地位制命名法，或是四舍五入. 当小数位数少时，这样处理固然可以，位数多了，就很不方便. 刘徽从长度记法入手，在长度的记法中用到单位名，丈、尺、寸、分、厘、毫、秒、忽，“忽”是最小的单位. 当现实中遇到精确到“忽”以下数位时，刘徽用十进分数形式表达，创造了具有非凡意义的十进小数.

刘徽在《九章算术注》中有3个地方用十进小数注释.

有了十进小数，无论有多少小数位，都能给出精确的表达. 而创造十进小数的过程，在小数部分的数位以100、101、102、…、10n为分母，就是逻辑推理思想的具体应用. 在开方术的注释中，他从开方不尽的意义出发，论述了无理方根的存在，并引进了新数，创造了用十进分数无限逼近无理根的方法.

严密的逻辑性，是数学学科的特点. 以几何教学为例，几何学习能力的培养，遵循图形的认识、图形与变换、图形与证明、图形与坐标这一逻辑进行，以逻辑推理为依托构建了几何学习的知识体系.

1.6 敢于挑战权威的创新思想

刘徽在“方程”章的注释中指出，有些人“拙于精理”,只知按前人的方法，亦步亦趋地去做，不懂得改变解题的方法和步骤，有的甚至于“或用算而布毡，方好烦而喜误，曾不知是非，反欲以多为贵”. 刘徽这一论述，尖锐地批评了当时数学上的“踵古”思想. 刘徽认为：“学者踵古，习其谬失”. 没有创新的思想，就没有学术的发展，就没有人类的进步. 刘徽敢于质疑，敢于提出新观点的优秀品质，是他为数学作出巨大贡献的内生动力.

例如在“方田”章“圆田术”的注释中，他指出圆周率“非周三径一之率也，周三者从其六觚之环耳”. 这句注释阐明，“周三”只是圆内接正六边形的周长，而不是圆的周长. 可是很多人还亦步亦趋地守着“周三径一”这个陈腐的概念，不敢超越.

刘徽的“割圆术”对数学知识体系的进一步完善具有重大意义. 不仅求得“徽率”，提高了圆周率的精度. 而且在将圆内接正多边形的边数逐次加倍，以使多边形面积逼近圆面积时，刘徽的“割之弥细，所失弥少. 割之又割，以至于不可割，则与圆合体，而无所失矣”，是刘徽极限思想的萌芽[6].

刘徽在《九章算术注》中提出了很多创新性算法及观点，虽然有些算法及观点还需要进一步的完善，甚至存在错误，却为后人的创造性探索积累了经验、留下了课题.

1.7 注重“直观性”在感性认识中的作用

刘徽注意到直观性在感性认识形成中的重要作用，他主张“析理以辞，解体用图”，理论的形成需要建立在直观的感性认识的基础上，只有这样，才能更好地形成数学知识体系. 因而，他在《九章算术注》中很注意使用图形、立体模型、剪纸和涂抹颜色等技巧.

例如对“正负术”的注释“今两算得失相反，要令正负以名之. 正算赤，负算黑”注释的意思是：现在要用算筹代表得失相反的两种量，就把表示“得”的算筹所代表的数叫正数，把表示“失”的算筹所代表的数叫作负数，并且把代表正数的算筹涂上红色，把代表负数的算筹涂上黑色. 刘徽在这句注释里不仅用“得”与“失”给正负数下了一个很好的定义，并且还从视觉上给正、负数算筹涂上不同颜色，便于人们直观地辨认和使用. 刘徽还认为“言负者未必负于少，言正者未必正于多”，这是说正负数的绝对值，前一句话是指负数的绝对值未必小，后一句话是指正数的绝对值也不一定很大. 在计算中，筹的总数不变，即筹的个数不变.

对于《九章算术》中的几何命题，刘徽常以“解体用图”的方法予以诠释和证明. 所谓“解体用图”就是利用图形的分解、合成、割补或移动位置等方法进行等积变换，从而证明原著的命题或计算公式是成立的.

数学教学中常用的图示法、列表法、模型制作法等，是刘徽“直观性感性认识”数学思想的具体应用.

2 为完善数学知识体系做出卓越贡献

在中国数学史上，刘徽第一次提出运用辩证法思维解不是唯一的一类方程，即“不定方程问题”的概念，并从辩证的角度提出并定义了许多数学概念：如幂(面积)、方程(线性方程组)、正负数等；在线性方程组解法中，他正确地提出了正负数的概念及其加减运算的法则，改进了线性方程组的解法；刘徽创造了比直除法更简便的互乘相消法，与现今解法基本一致；他推导出等差级数前n项和公式；在“勾股”章的注释中，刘徽不仅论证了有关勾股定理与解勾股形的计算原理，发展了勾股测量术，还提出了相似勾股形理论，通过对“勾中容横”与“股中容直”之类的典型图形的论析，形成了中国特色的相似理论. 他用比率理论建立了数与式的统一的理论基础，应用出入相补原理和极限方法解决了许多面积和体积问题，为中国数学发展做出了卓越的贡献.

刘徽的数学成就，不仅对中国古代数学发展产生了深远影响，而且在世界数学史上也被很多外国学者称作“中国数学史上的牛顿”. 在世界数学史上，他最早提出十进小数概念，并用十进小数来表示无理数的立方根；在开方不尽的问题中提出“求徽数”的思想，这种方法与后来求无理根的近似值的方法一致；他还用“率”来定义中国古代数学中的“方程”，即现代数学中线性方程组的增广矩阵.

《九章算术》虽然体系不甚完整，一些算法还存在问题，但仍然是中国古代数学的瑰宝，并为世界数学的发展做出了重要的贡献. 刘徽的《九章算术注》让中国古代数学体系走向规范，不仅给人类留下开创性的数学定义、命题与原理，他在注释过程中彰显的辩证法、在不同的数学问题中挖掘一般规律、用不同的方法解决相同问题、复杂问题转化、逻辑推理、敢于创新等思想方法，成为激励人们不断探索未知的精神财富.