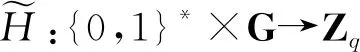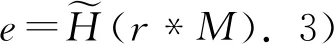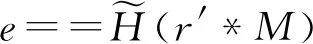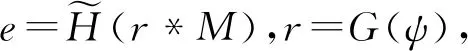新分数阶算子及其在密码学上的应用
2020-06-28陈兴发姚正安
陈兴发, 姚正安
(1. 广东第二师范学院 数学系, 广东 广州 510303; 2. 中山大学 数学学院, 广东 广州 510275)
0 引言
现代密码学理论大多建立在数论和交换群理论上. 例如:Diffie-Hellman密钥协商方案[1]的安全性与离散对数求逆问题的困难性有关; RSA公钥加密方案的安全性与大素数分解问题的困难性相关. 目前Diffie-Hellman密钥协商方案和RSA公钥加密方案广泛应用在电子商务中. 这些公钥的密码学系统都是基于密码学里的一个重要构造──单向函数. 简单来讲,单向函数f:A→B,是已知x∈A,计算f(x)∈B是容易的,但已知y=f(x)∈B,求x′∈x,满足f(x′)=y是困难的. Diffie-Hellman密钥协商方案中的离散指数就是单向函数的例子.
然而,Peter Shor[2]证明了量子计算机能在多项式时间里求解离散对数求逆问题和大素数分解问题. 2019年10月23日,美国科技巨头谷歌在《自然》杂志上刊登论文[3],宣称其量子计算机已经实现了“量子霸权”. 一旦量子计算机研制成功,这些基于离散对数求逆问题和大素数分解问题构造的密码系统会被攻破. 量子计算的快速发展给经典密码学带来了巨大冲击,使得人们将目光投向了能够抵抗量子计算机的攻击的密码体制研究[4].
G.B Blakley[5]提出将分析数学应用到密码学中,利用偏微分方程理论构造热流密码体制. Hungerbühler[6]利用热传导方程:
(1)
构造了一个基于热力学第二定律的单向函数,并且说明了这个单向函数能够抵抗量子计算机的攻击.
基于离散对数求逆问题和大素数分解问题构造的密码系统是离散的,数据精确到一个比特值,只要有一个比特的值改变了都导致无法正常解密或验证. 而基于偏微分方程的密码系统是连续的,允许有一定的冗余,数据出现微小变化时,系统仍然可以正常解密或验证. 这样的性质使得连续的密码系统可以在生物识别技术中有广泛的应用,因为人的生物特征如指纹、虹膜以及声音等随着时间会有微小变化,生物识别系统允许特征有微小变化的人通过,而其他显著不同的就不能通过了.
我们用As代替方程(1)中的(-△)算子,并将方程(1)的边界改为周期边界:
(2)
然后说明方程(2)的解是适定的,但其反问题是不适定的,由此构造出一个单向函数,并将其应用到数字签名上.
1 基础知识
1.1 基本不等式
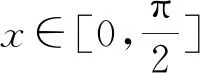
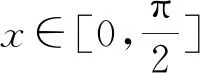
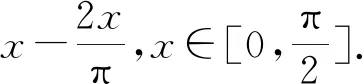
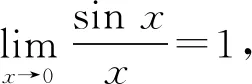
1.2 卷积的傅里叶级数
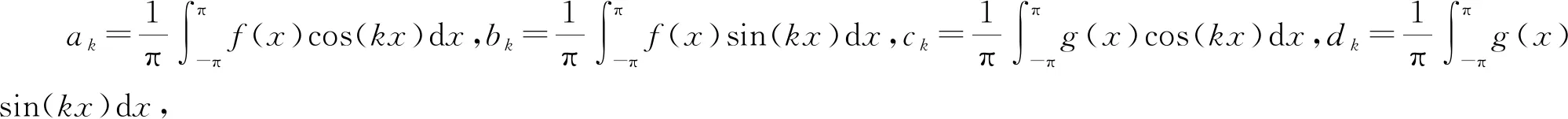
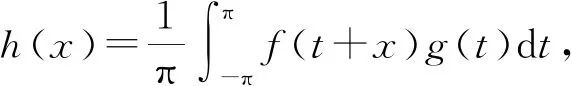
而
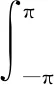
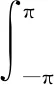
所以h(x)的傅里叶展开在x=x0处收敛于h(x0),从而有
1.3 圆上的Hilbert变换
设u在单位圆内调和,则存在解析函数h且
h(z)=u(z)+iv(z), |z|<1,
v是u的共轭调和函数,由C-R条件知v的共轭调和函数是-u. 根据泊松公式可得
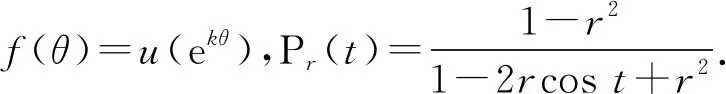
则
当r→1时,
因此式是奇异积分,取主值意义,有
上述变换具有以下性质[7-9]:
1)若f∈Lp,1 2)若|f(θ+δ)-f(θ)|≤K|δ|α,则|H(f)(θ+δ)-H(f)(θ)|≤C|δ|α. 首先利用圆上的Hilbert变换得出对以2π为周期的函数u(x)求二次导数的积分形式. 定理1若u(x)是2π为周期,且具有二次导数,则 证明希尔伯特变换可得 而 又 则 由定理1可以定义一个新的分数阶算子As. 定义1 (3) 下面的引理4说明当u满足一定条件时,As(u(θ))∈L([0,2π]). 引理4若u(x)∈C1,a,0≤s<2且a-s>-1,则存在M>0使得 I1的积分区域里没有瑕点,所以绝对可积,存在M1>0使得I1≤M1. 对于积分I2,当ε充分小时,利用微分中值定理和引理2可得 其中:x+α<ξ 由对称性可知存在M3>0使得I3≤M3. 对于积分I4,当ε充分小时,利用u(x)∈C1,a和引理2可得 定理2若C是常数,则As(C)=0,对任意n∈Z. 证明若C是常数,显然As(C)=0.下面计算As(cos(nx)). 其中: g(x,α,β)=cos(nx+nα+nβ)-cos(nx+nα)-cos(nx+nβ)+cos(nx)= 故 记 则 而 记 则 P(x)=-2Tn,ssin(nx), 记 下面计算Q(x). 最后 同理可得 定理2说明,常值函数、sin(nx)和cos(nx)(n∈Z)是As的特征向量. 下面估计Tn,s的界. 证明 下面的定理4说明了As具有分数阶性质. 证明先证Tn,s>Csns-1. 而 故 然后证明Tn,s≤C′sns-1. 利用引理2可得 I1≤C′1,sns. 同样利用引理2,注意s>1,可得 所以I1≤C′2,sns. 综上所述可知Tn,s≤C′sns-1. 其中:M1,s是仅与s相关的常数. 其中:M2,s是仅与s相关的常数. 证明计算As(u(x))可以分为3步: 1)I1(α,β,x)=Δα,β(u(x))=u(x+α+β)-u(x+α)-u(x+β)+u(x). 由计算As(sin(nx))的过程知 同理可得 综上所述 类似地,可以得到定理6. 结合上述两个定理,可得到推论1. As:HsL[0,2π], u(x) 证明f(x)∈Hs,g(x)∈Hs,则由Hs的定义可知f*g∈Hs. 结合引理3和推论1可知 其中: 当k=0时,R0(C)恒为常数. 所以 下面讨论方程 (4) 其中: 的解 同时由推论1可知 所以这样的u(t,x)满足方程(4). 定理10方程(4)的解 是稳定和唯一的. 证明方程两边同乘u,并且对空间积分和时间积分可得 所以 假设 的解为uε(x),则可得 令φε(x)=φ(x)+ε,0<ε,得 即|u(t,x)-uε(t,x)|<ε,解的稳定性得证. 假设方程有解u1、u2,则u=u1-u2也是方程的解,由上述计算可得 不等式右端为零,则u1=u2,方程解的唯一性得证,即方程是适定的. (5) 定理12方程(4)的反问题,即已知 (6) 证明u(0,x)是不适定的. 当t=T时, 设方程(4) 在T时刻的解为ω(x)=u(T,x). 1)连续性:由方程(4)的解的适定性(定理10)可知映射Gs,T是连续的. 2)线性性质:由于方程(4)是齐次方程,由解的叠加原理可知Gs,T(φ+ψ)=Gs,T(φ)+Gs,T(ψ). 3)卷积作用性质:由定理11可得Gs,T(φ*ψ)=Gs,T(φ)*ψ. 4)求逆困难:由定理12可知,在已知ω的情况,求φ满足Gs,T(φ)=ω是困难的. 5.2.1Schnorr签名方案[10] 由表1可以知道,Gs,T在某种程度上可以代替离散对数. 现将Gs,T应用到Schnorr签名方案[10]中,得到基于新分数阶算子签名方案. 表1 Gs,T与离散对数 5.2.2基于新分数阶算子签名方案 密钥生成:签名私钥φ,公钥Y=Gs,T(φ). 签名验证的正确性: 在文献[11]中证明了在随机预言模型下只要离散对数求逆是困难的,Schnorr签名方案就是不可伪造的. 在文献[12]中证明了在随机预言模型下所有基于单向群同态的类Schnorr型签名方案是不可伪造的. 所以我们提出的基于新分数阶算子签名方案在随机预言模型下也是不可伪造的,而且是基于一个更难的单向函数问题.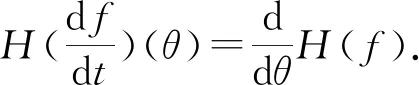
2 新分数阶算子的定义
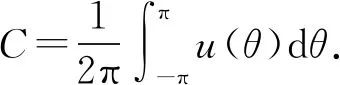
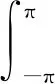

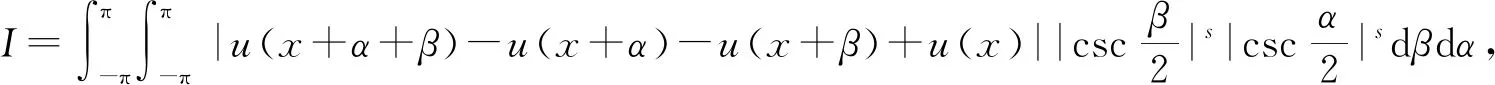
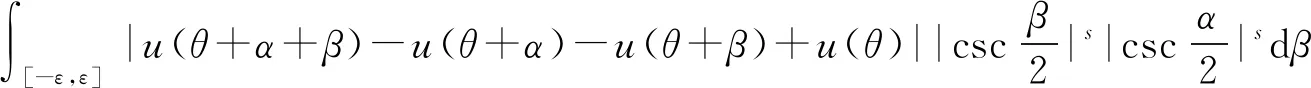
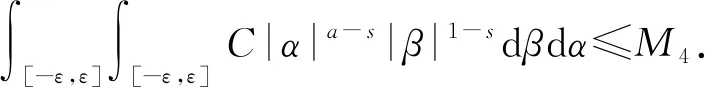
3 新分数阶算子的性质
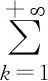
3.1 新分数阶算子的特征向量
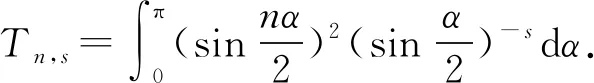
3.2 新分数阶算子的特征值的估计
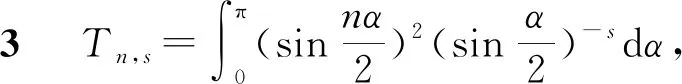
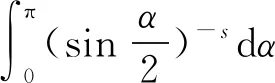
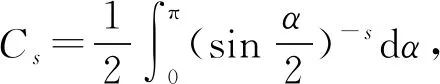
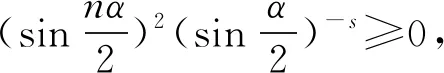
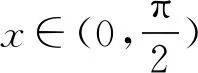
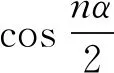
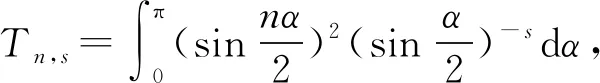
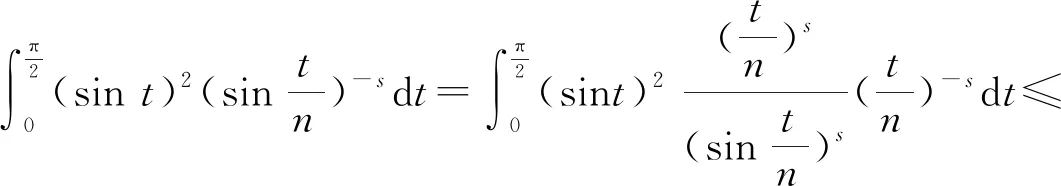
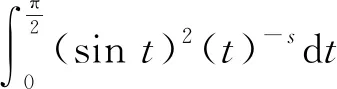
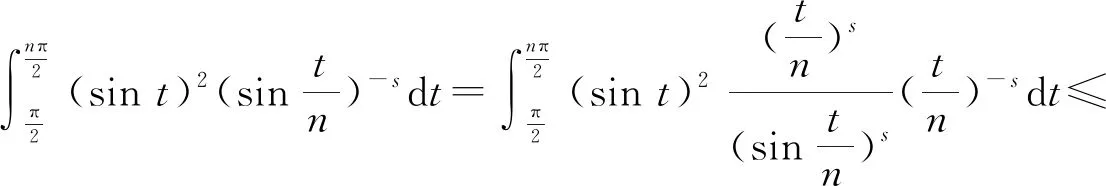
3.3 新分数阶算子的分析性质
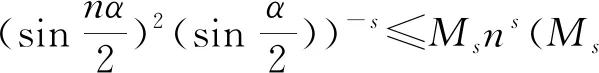
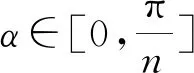
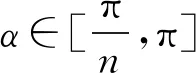
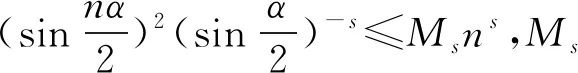
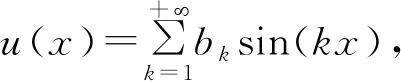
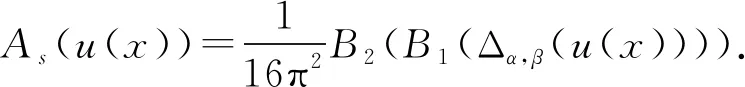
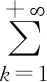
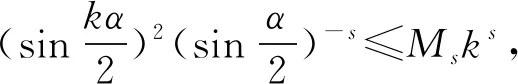
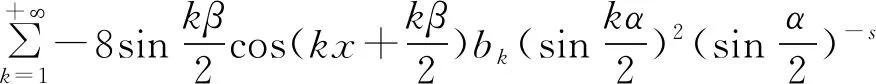
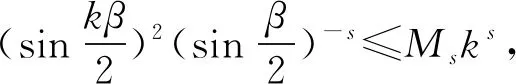
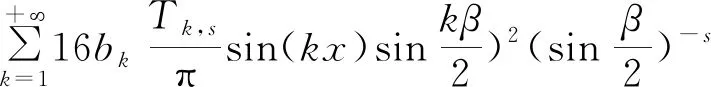
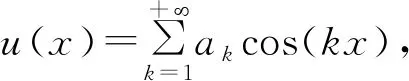
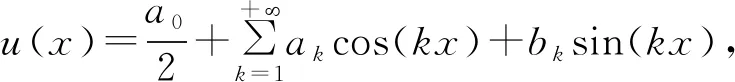
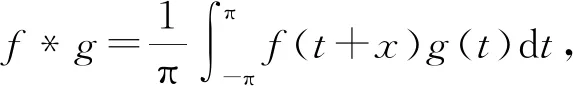
3.4 新分数阶算子的傅里叶系数
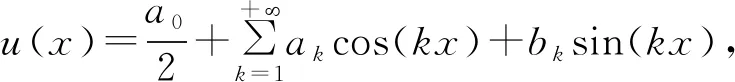
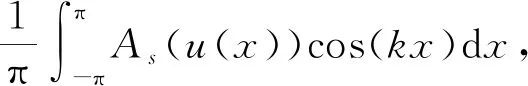
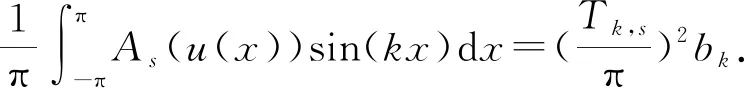
4 新分数阶算子抛物型方程
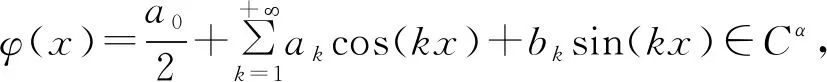
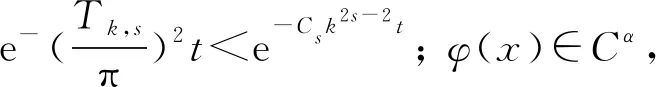
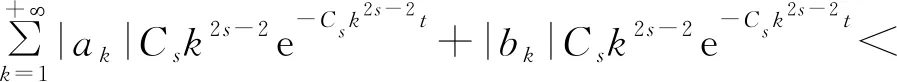
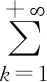
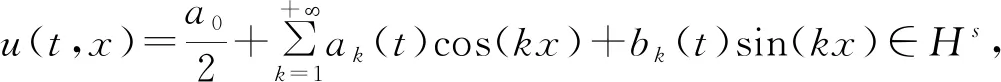
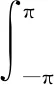
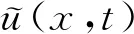
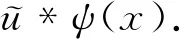
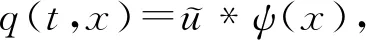
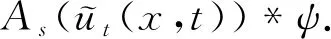
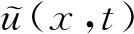
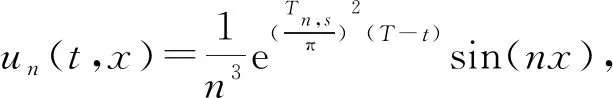
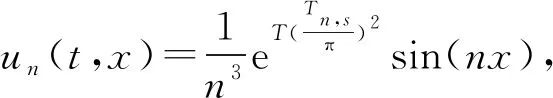
5 新分数阶算子在密码学中的应用
5.1 基于新分数阶算子抛物型方程的单向函数
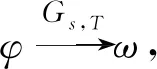
5.2 基于新分数阶算子签名方案