关于Neuman-Sándor平均的一个最优组合界
2020-06-28何灯吴善和
何灯, 吴善和
(1. 福清第三中学, 福建 福清 350315; 2. 龙岩学院 数学与计算机科学学院, 福建 龙岩 364012)
0 引言
两个正数a,b(a≠b)的幂平均定义为

两个正数a、b(a≠b)的调和平均,指数平均,对数平均,形心平均,反调和平均分别定义为

两个正数a、b(a≠b)的Schwab-Borchardt平均SB(a,b)[1-2]定义为

其中:P(a,b)为第一类Seiffert平均,T(a,b)为第二类Seiffert平均,M(a,b)为Neuman-Sándor平均,L(a,b)为对数平均.
上述所列平均有如下熟知不等式链:
H(a,b) M(a,b) 近几年,Neuman-Sándor平均和其他二元平均得到深入的研究. 特别地,从有关Neuman-Sándor平均与其他二元平均或它们的各类组合比较中发现了许多重要的结论,参见文[1-16]. 关于Neuman-Sándor平均的下界估计,形式简洁且较强的有如下结论: 关于Neuman-Sándor平均的上界估计,形式简洁且较强的有如下结论: 综合上述结论进行比较分析,可得Neuman-Sándor平均的如下最强上下界估计: (1) 笔者在研究中发现,式(1)上界可作改进,实际上有如下更强的双边不等式: (2) 显然,算术平均A(a,b)与第二类Seiffert平均T(a,b)能够更精确构造出Neuman-Sándor平均M(a,b)的上下界. 在式(2)的基础上,本文研究如下双边不等式: αT(a,b)+(1-α)A(a,b) 给出此不等式对所有不同正实数a和b成立的最大α值及最小β值. 则g2(x)关于x在(0,1)上单调递增,从而g2(x)>g2(0)=0. 则 (1+x2)(10 000+7 600x2+2 019x4-139x6)2-(100+63x2+3x4)4>(<0)⟺ 3 350 000-709 000x2-2 278 685x4-767 087x6+12 517x8-81x10>(<0). 令g5(x)=3 350 000-709 000x2-2 278 685x4-767 087x6+12 517x8-81x10,计算得 g′5(x)=-1 418 000x-9 114 740x3-4 602 522x5+100 136x7-810x9< -4 602 522x5+100 136x5<0, 则g5(x)关于x在区间(0,1)内单调递减,注意到g5(0)·g5(1)<0,由零点存在定理得g5(x)在(0,1)内存在唯一零点,设为x0,则当x∈(0,x0)有g5(x)>0,g′4(x)>0,当x∈(x0,1)有g5(x)<0,g′4(x)<0. 综上,可得g4(x)在区间(0,1)内先增后减,从而 引理3得证. 证明将待证不等式变形,等价于证明 即证 (1+x2)(300+139x2)2(100+13x2-36x4-2x6)2-(3-2x2)2(100+63x2+3x4)4>0⟺ g7(x)+g8(x)>0. 其中: g7(x)=-324x18+51 040x16+2 373 523x14-201 359 151x8-595 105 800x6, g8(x)=27 437 168x12+47 121 658x10+10 260 000x4+1 218 000 000x2+900 000 000. 由于 g7(x)>-324-201 359 151-595 105 800=-796 465 275,g8(x)>900 000 000, 则g7(x)+g8(x)>-796 465 275+900 000 000>0,从而F1(t1)>0,引理4得证. 证明计算得 其中: g9(x)=607 500+804 600x2+218 637x4-36 271x6-6 732x8>607 500-36 271-6 732>0. 则定理5成立. 引理6若x∈(0,1),记 g10(x)=54(450+223x2)(6x2+25)(100+63x2+3x4)2, g11(x)=(300+139x2)(11 664x10+974 835x8+8 571 892x6+29 034 750x4+ 41 152 500x2+20 250 000), 证明借助于数学软件的辅助计算,可得 其中: g12(x)=422 848 471 824x10+38 543 819 989 824x8+1 227 891 635 120 340x6+ 13 257 228 349 412 739x4+67 557 540 066 375 960x2+178 105 636 717 830 500>0, g13(x)=6 089 703 722 617x8+2 162 065 917 900x6-2 107 376 977 500x4- 721 615 500 000x2+917 325 000 000. 注意到 g13(x)>6 089 703 722 617x8-2 107 376 977 500x4-721 615 500 000+917 325 000 000= 6 089 703 722 617x8-2 107 376 977 500x4+195 709 500 000≥ 定理1双向不等式 αT(a,b)+(1-α)A(a,b) (3) 得式(3)等价于 其中: 其中: 从而可得 通过对Neuman-Sándor平均M(a,b)上、下界的比较分析,笔者发现了算术平均A(a,b)与第二类Seiffert平均T(a,b)能够更精确构造出M(a,b)的上下界,在此基础上建立M(a,b)的一个最优组合界. 此种研究方法可借鉴于寻求P(a,b),T(a,b)及L(a,b)等平均的更优上下界,此将另文叙述.
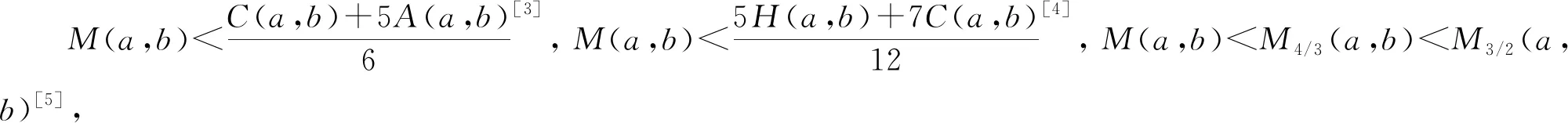
1 引理及证明


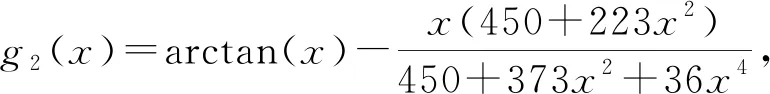
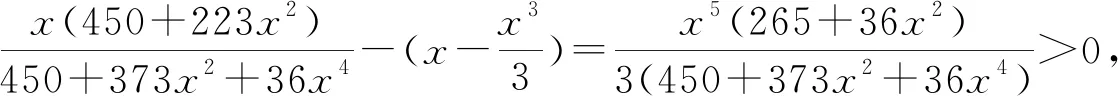
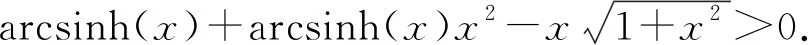



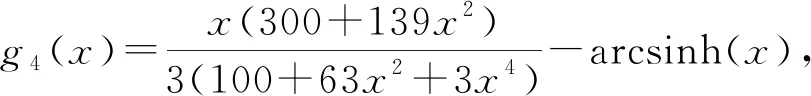
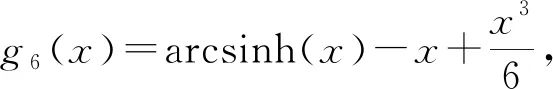
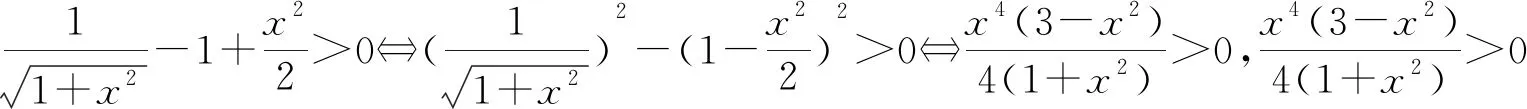




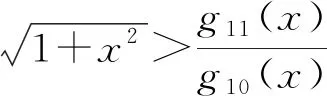
2 主要结论及证明
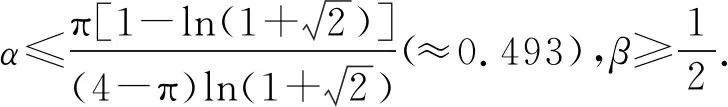
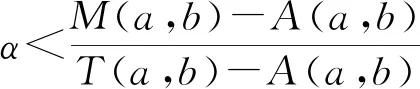
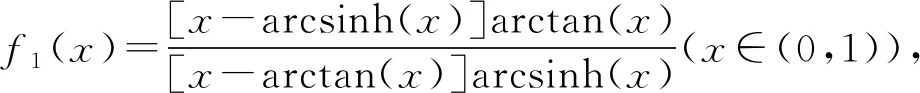






3 结语
