齐次核的Hilbert型积分不等式的研究进展与现状
2020-06-28洪勇
洪勇
(1. 广东白云学院 数学教研室, 广东 广州 510450; 2. 广东财经大学 统计与数学学院, 广东 广州 510320)
0 引言
1908年和1911年,著名数学家Hilbert和Schur先后证明了不等式:
两式中的常数因子π都是最佳的. 由于这两个不等式分别与级数算子和积分算子有紧密的联系,由此它们有重要应用价值. 特别是近代调和分析采用算子理论作为基本研究方法后,更加突显了这类不等式的理论意义,从而进一步促进了对这两个不等式的研究,形成了一套Hilbert型不等式的理论体系.
本文针对齐次核的Hilbert型积分不等式理论体系由浅入深、由特殊到一般、由具体到抽象的形成过程,结合作者的研究成果,陈述其研究历程及目前的研究现状,展示了齐次核的Hilbert型积分不等式的3个发展阶段.
1 Hilbert型积分不等式与权系数方法
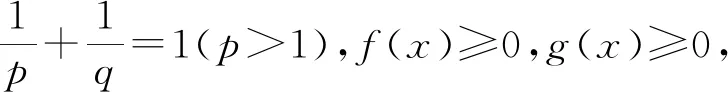
(1)
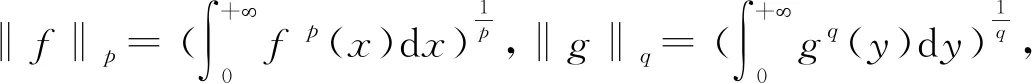
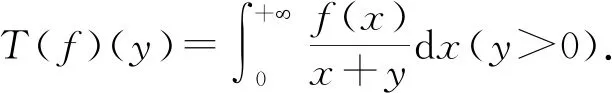
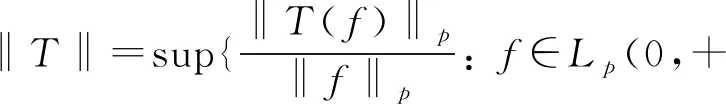
因此对式(1)的研究具有重要的理论意义和实际应用. 于是引入多个参数,对式(1)进行改进、推广和向高维发展的研究随之展开.
近100年来,特别是最近20年,经国内外学者杨必成、匡继昌、洪勇、高明哲、Mitrino J E、Pecaric J E等的努力,取得了丰硕的成果,在国内外重要期刊上发表了数百篇的学术论文.
之所以近20年内,Hilbert型不等式的研究能够取得重大进展,很大程度上也得益于徐利治先生在[2]中提出的权系数方法,其基本思想是:
设r>0,α∈R,记
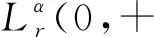
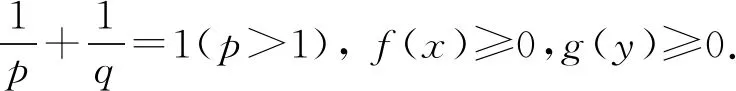
选取参数a、b,根据Hölder不等式,有
其中:权函数ω1(x)及ω2(y)为

于是
记α=λ+ap-bp+1,β=λ+bq-aq+1,则得到Hilbert型积分不等式:
(2)
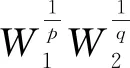
选取适配参数有较强的技巧,是得到最佳Hilbert型不等式的关键所在.
定义奇异积分算子T为
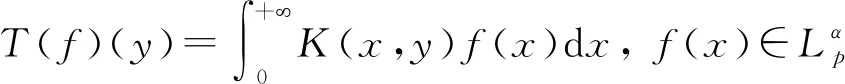
(3)
则可以证明式(2)等价于
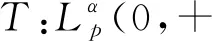
2 Hilbert型积分不等式研究的第一阶段
这个阶段持续时间最长,多年来,特别是从徐利治先生提出权系数方法以来,以杨必成为首的一大批学者取得了大量的成果,其特点是:针对一些具体的齐次核,技巧性地进行参数搭配,通过对权函数精确细致的估算,得到若干具有最佳常数因子的Hilbert型积分不等式,同时也对式(1)进行改进与推广.
选取适配数a=b=(1-λ)/4,2000年文[3]引入多个参数得到定理1.
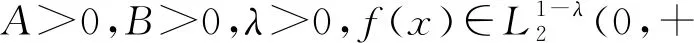
这个定理的意义在于较早引入多个独立参数,用权系数方法得到了齐次核的具有最佳常数因子的Hilbert型不等式,为后来的进一步研究提供了范例.
选取适配数a=b=(1-λ)/(pq),文[4]得到定理2.
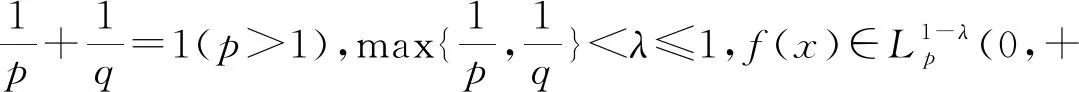
其中的常数因子是最佳的.
选取适配数a=(1-λ)/q2,b=(1-λ)/p2,文[5]得到定理3.

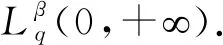
其中的常数因子是最佳的.
根据定理2和定理3,选取不同的适配数进行不同的参数搭配可以得到同一个齐次核的不同的Hilbert型积分不等式,且常数因子都是最佳的.
选取适配数a=b=(2-λ1λ2)/(pq),可得定理4.
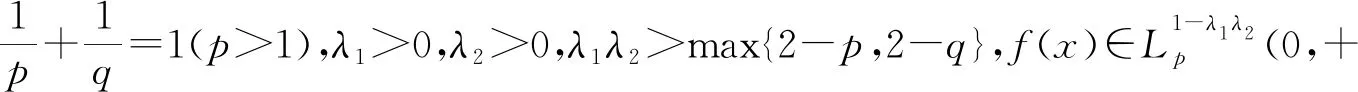
其中的常数因子是最佳的.
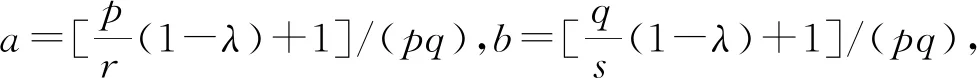
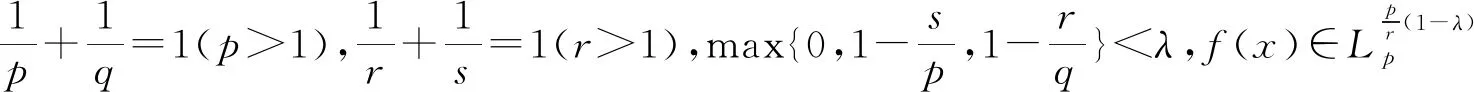
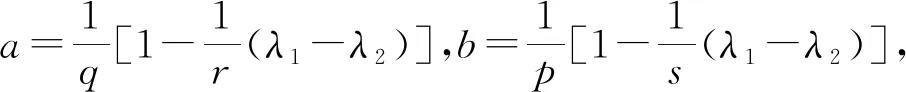
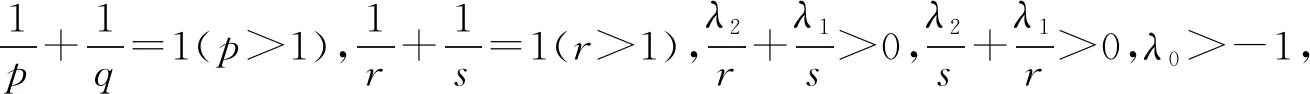
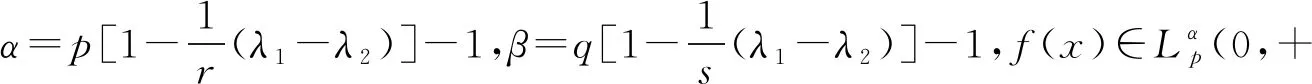
更多的相关结果,可以参见文 [6-12].
3 Hilbert型积分不等式研究的第二阶段
利用权系数方法研究Hilbert型积分不等式时,要使所得的不等式具有最佳常数因子,不仅需要精细的对权函数的估算,更关键的还在于搭配参数a、b的选取. 那么怎样选取a和b使之能成为适配数呢?前面的研究都是基于作者丰富的经验而得到的. 经过对大量文献的分析和探索,2016年文[13]完美地解决了这一问题,虽然文章是针对级数不等式而言的,但易知对积分不等式仍然适用.
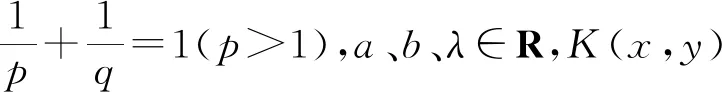

都收敛. 则
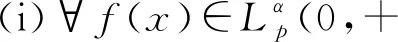
(4)
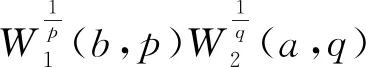
该结果的出现,将齐次核的Hilbert型积分不等式的研究推向了一个新的阶段. 其特征是:选取a、b满足bp+aq=λ+2,可以成批地得到相应的Hilbert型积分不等式.
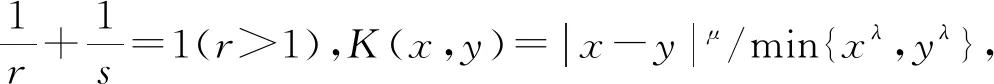
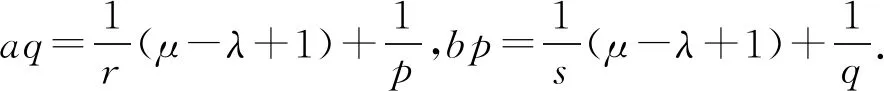
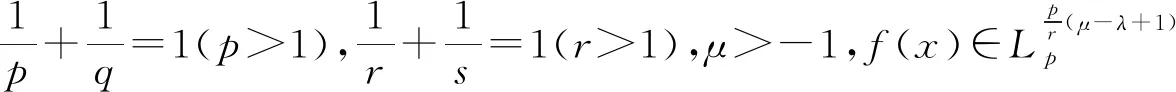
又由于bp+aq=(μ-λ)+2也可写为
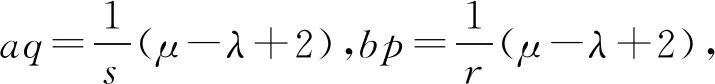
由于bp+aq=(μ-λ)+2还可写为
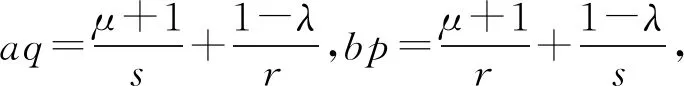
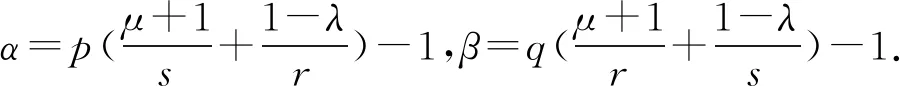
设K(x,y)=|ln(x/y)|/max{xλ,yλ},则K(x,y)是-λ阶齐次非负函数. 因为bp+aq=2-λ可写为.
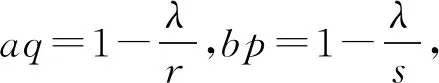
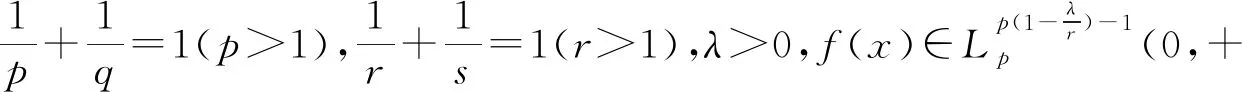
其中的常数因子是最佳的.
4 Hilbert型积分不等式研究的第三阶段
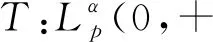
(5)
成立. 若要进一步求出算子范数,还需讨论当式(5)成立时,其最佳常数因子是多少?
这些问题的讨论显然是更深入更具重要意义的,可喜的是2017年文[14]得到定理10.
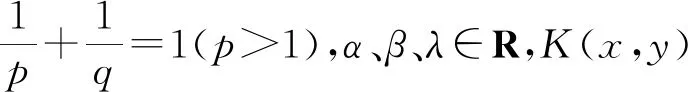
(6)
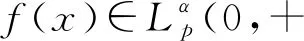
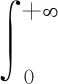
由此可得到:当且仅当λ=-1即当K(x,y)是-1阶齐次非负函数时,T是Lp(0,+)到自身的有界算子.
在这个阶段,可构造出齐次核下的所有Hilbert型积分不等式,只需取特定的K(x,y)并计算出
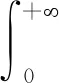
取0阶齐次核的非负函数:
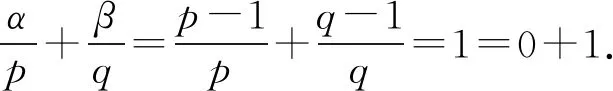
于是可得定理11.
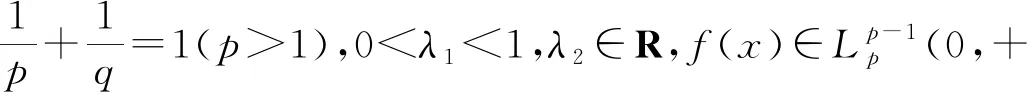
取-λ阶齐次非负函数:
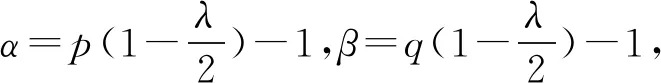
于是可得定理12.
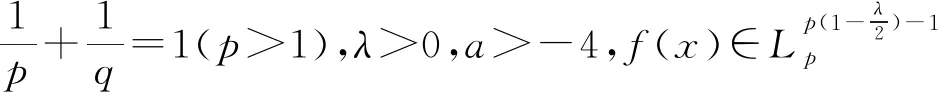
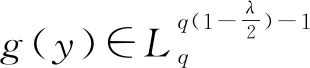
利用上述方法构造齐次核的具有最佳常数因子的Hilbert型积分不等式,主要工作就是计算积分


5 结语
在研究齐次核的Hilbert型积分不等式的过程中,许多学者同时也讨论一些非齐次核的情况,当然还考虑Hilbert型级数不等式、半离散Hilbert型不等式,并将相关结果推向高维情形. 限于篇幅,对这些方面的研究进展与研究现状,笔者将在另文陈述.
