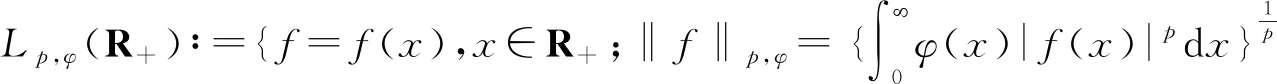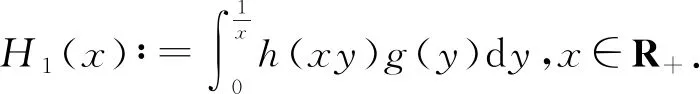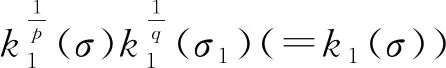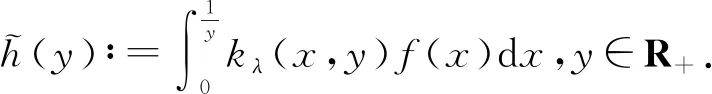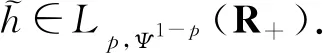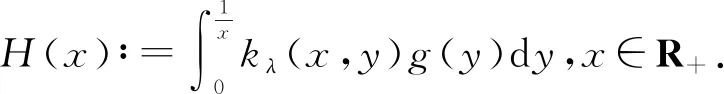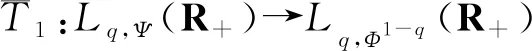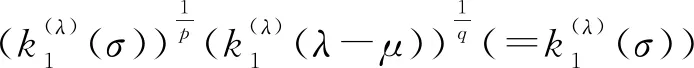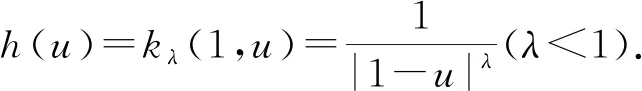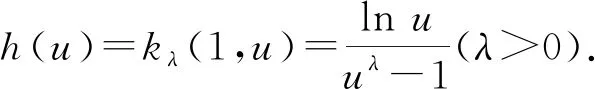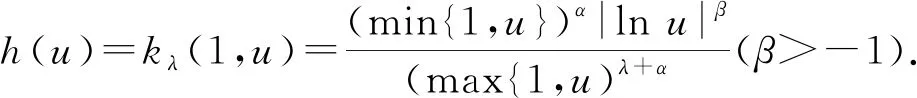第一类Hardy型积分不等式的等价性质及其应用
2020-06-28杨必成
杨必成
(广东第二师范学院 数学系, 广东 广州 510303)
0 引言
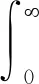
(1)
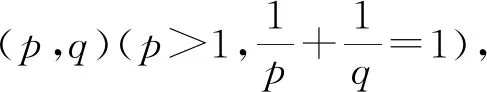
(2)
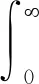
具有最佳常数因子kp的Hardy-Hilbert型积分不等式:
(3)
在式(3)的条件下,Hardy等[3]在定理350中还考虑了如下非齐次核的情形:设
(4)
1998年,杨必成[4-5]引入独立参数λ>0及Beta函数,推广式(1)为
(5)
(6)
当λ=1、r=q、s=p时,不等式(6)变为式(2);当λ=1、r=p、s=q时,不等式(6)变为如下式(2)的对偶形式:
(7)
2009年,文[7-8]还利用引入独立参数及两对共轭指数的方法,推广式(3)及式(4)为一般-λ齐次核的形式,并建立了两类Hardy型积分不等式. 文[9-10]还给出了多重方面的应用.
2016-2017年,洪勇等[11]建立了一般齐次核离散Hilbert型不等式最佳常数因子的联系参数的等价陈述;洪勇[12]还考虑了一般齐次核Hilbert型积分不等式成立的联系多参数的等价条件;杨必成[13]考虑了逆向Hardy型不等式的类似情形;2019年,杨必成[14-15]给出了积分及半离散Hilbert型不等式最佳常数因子联系参数的若干等价陈述. 类似的结果可参阅文[16-20].
本文引入若干独立参数,应用实分析的思想技巧,建立一个一般非齐次核第一类Hardy型积分不等式,还建立了它的等价式及联系最佳常数因子与多参数的若干等价陈述,并导出齐次核第一类Hardy型的情形. 作为应用,给出其算子表示及若干特殊核的例子.
1 若干引理
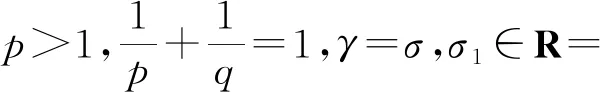
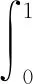
又设f(x)、g(y)在R+上为非负可测函数,使
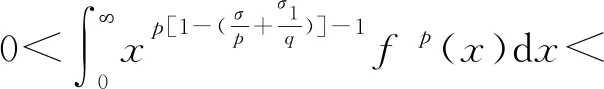
(8)
引理1如下非齐次核第一类Hardy型积分不等式成立:
(9)
证明定义如下权函数:
(10)
固定x,作积分变换u=xy,可求得
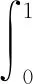
(11)
同理,由对称性,可算得
(12)
应用Hölder积分不等式[21]、Fubini定理[22]、式(10)及式(12),有
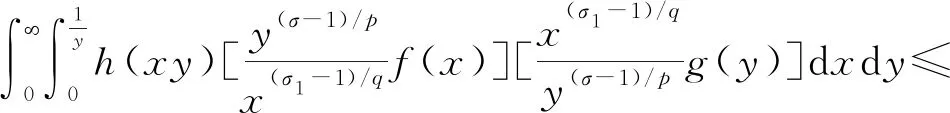
下证此式取严格不等号. 若取等号,则存在不全为零的常数A和B,使[21]
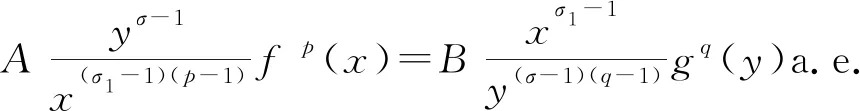
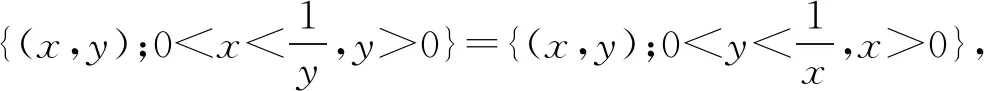

注1若σ1=σ,则式(8)及不等式(9)变为:若
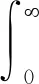
则有如下简化的第一类Hardy型积分不等式:
(13)
引理2不等式(13)的常数因子k1(σ)是最佳的.
证明任给ε>0,设
若有正常数M(≤k1(σ)),使之取代k1(σ)后,式(13)仍成立,则特别地,有如下不等式:
可求得
还可求得
故M=k1(σ)为式(13)的最佳值. 证毕.

(14)
应用带权的Hölder不等式,还成立如下不等式[21]:
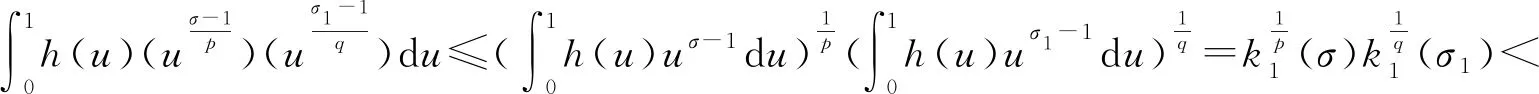
(15)

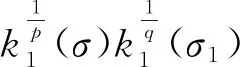
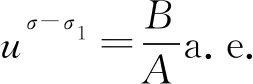
2 等价形式及若干等价陈述
定理1不等式(9)等价于下列积分不等式:
(16)
(17)
且式(16)与式(17)的常数因子是最佳值的等价条件是式(9)的相同常数因子也是最佳值.
特别地,若σ1=σ,则有具有最佳常数因子的式(13)及如下与之等价的积分不等式:
(18)
(19)
证明若有式(16),则由Hölder积分不等式[21],有
(20)
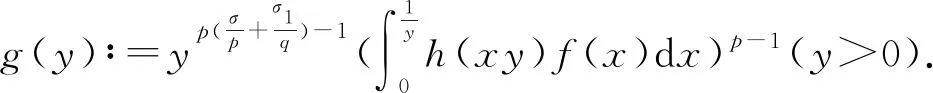
(21)
若J1=0,则式(16)必然成立;若J1=,则式(16)不可能成立,即有条件J1<. 下设0 即有式(16),且它与式(9)等价. 同理,可证得式(9)与式(17)亦等价. 故式(9),式(16)与式(17)齐等价. 若式(9)的常数因子为最佳值,则由式(19)可导出式(16)的常数因子也为最佳值. 不然,则能导出式(9)的常数因子不为最佳值的矛盾. 同理,用反证法,若式(16)的常数因子为最佳值,则式(9)的常数因子也必为最佳值. 不然,由式(21),则能导出式(16)的常数因子也不为最佳的矛盾. 因而式(16)的常数因子是最佳值等价于式(9)的常数因子也是最佳值. 同理可证式(17)的常数因子是最佳值当且仅当式(9)的常数因子也是最佳值. 故式(16)及式(17)的常数因子是最佳值等价于式(9)的相同常数因子也是最佳值. 证毕. (22) (23) (24) 定理2下列陈述等价: (iii)σ1=σ; (ii)⟹(iii). 由(ii),式(15)取等号. 则由引理3, 可得关系式σ1=σ. 故陈述(i)、(ii)、(iii)及(iv)等价. 证毕. 则有下面等价的齐次核第一类Hardy型积分不等式: (25) (26) (27) 且不等式(25)的常数因子是最佳值等价于式(26)及式(27)的常数因子也是最佳值. (28) (29) (30) (31) (32) (33) 推论2下列陈述等价: (III)μ+σ=λ; 定义如下实赋范线性空间: 于是还有 即h1∈Lp,ψ1-p(R+). 定义1定义一个非齐次核第一类Hardy型积分算子T1:Lp,φ(R+)→Lp,ψ1-p(R+)为:对任意f∈Lp,φ(R+),唯一对应h=T1f∈Lp,ψ1-p(R+). 定义T1f与g∈Lq,ψ(R+)的形式内积及算子T1的范数为 即H1∈Lq,φ1-q(R+). 由定理1、定理2,有推论3. 推论3若f(>0)∈Lp,φ(R+),g(>0)∈Lq,ψ(R+),则有如下等价不等式: (34) (35) (36) 还可定义实赋范线性空间:Lp,Φ(R+)、Lq,Ψ(R+)、Lp,Ψ1-p(R+)及Lq,Φ1-q(R+). 即H∈Lq,Φ1-q(R+). 由推论1、推论2,有 推论4若f(>0)∈Lp,Φ(R+),g(>0)∈Lq,Ψ(R+),则有如下等价不等式: (37) (38) (39) 当γ=σ、σ1∈(0,)时, 由推论3,当且仅当σ1=σ时, 由推论4,当且仅当μ+σ=λ时, 当γ=σ、σ1∈(0,)时, 由推论3,当且仅当σ1=σ时, 由推论4,当且仅当μ+σ=λ时, 当γ=σ、σ1∈(-α,)时, 由推论3,当且仅当σ1=σ时, 由推论4,当且仅当μ+σ=λ时,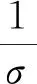

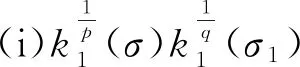


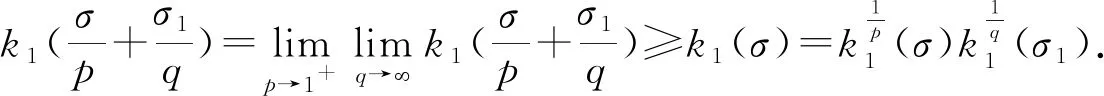

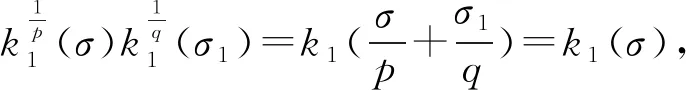

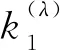

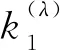
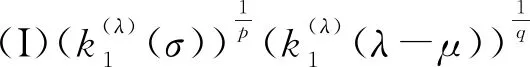
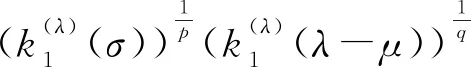
3 算子表示及若干特例