空间机器人捕获卫星操作基于柔顺装置的无源模糊避撞柔顺控制

艾海平，陈 力

(福州大学 机械工程及自动化学院，福州 350116)

1 引 言

近年来随着人类探索太空的进一步深入，空间任务日益增多，考虑到太空环境的恶劣性，宇航员出舱进行操作任务会面临很大的危险，利用空间机器人系统来替代宇航员完成空间失效卫星的维修、在轨燃料加注和在轨装配等操作任务成为较佳的选择，并引起了众多学者的关注[1-6]。同时，由于失效的卫星将影响空间任务的执行，考虑到空间资源的宝贵及卫星回收的经济效应，空间机器人捕获失效卫星操作的研究具备重要意义[7-9]。

Gasbarri等[10]介绍了用于预抓取及抓取后的两种控制策略。Virgili-Llop等[11]提出了一种基于凸形编程的制导算法，实现了对翻滚卫星的捕获。程靖等[12]讨论了空间机器人捕获卫星操作后姿态管理及其后辅助对接操作的协调控制问题，提出了一种基于极限学习机的自适应控制方案。Stolfi等[13]研究了捕获非合作柔性卫星的参数辨识问题，并采用阻抗算法对末端执行器进行控制。Lampariello等[14]提出了一种非线性优化控制方法，以实现有限时间内对翻滚目标的抓捕。

虽然上述学者对空间机器人系统捕获卫星操作技术的动力学及控制问题进行了研究，但是以上研究多停留在捕获前运动轨迹规划及捕获后镇定控制上。考虑空间机器人捕获卫星时，两者不可避免会发生接触和碰撞，在此过程中，空间机器人的机械臂关节处将会受到很大的冲击力矩，由于关节电机只能承受一定范围内的力矩，若所受冲击力矩超过其能承受的极限值，将造成电机的过载或损坏。因此，在捕获操作过程中采取一定措施以避免空间机器人最薄弱的部位(关节电机)受到这种冲击而损坏是极其必要的。然而，目前针对保护空间机器人关节免受捕获操作产生的冲击载荷破坏的研究鲜见报道，故对其研究有着重要的探索价值。

为了实现空间机器人捕获卫星过程保护关节不受捕获操作产生的冲击载荷的破坏，本文尝试将RSEA(Rotary Series Elastic Actuator)装置引入到空间机器人系统中，同时设计与之配合的控制策略以实现避撞柔顺控制。这是因为，RSEA装置可以在机械臂与外界环境发生接触和碰撞时很好地保护机器人的关节[15,16]，并有效缓冲和减小捕获操作产生的冲击能量，进而实现捕获操作阶段对关节电机的保护。考虑RSEA装置的引入，空间机器人系统的关节将具备柔性，关节的柔性将导致系统产生弹性振动，若不对该弹性振动进行主动抑制，很可能导致系统失稳，进而影响捕获任务的进行。

针对弹性振动的主动抑制，本文基于奇异摄动思想，将捕获后的混合体系统分解为快变子系统及慢变子系统。针对快变子系统，设计了基于速度差值反馈的控制器，以实现对系统弹性振动的主动抑制。针对慢变子系统，提出了一种基于无源性的模糊滑模镇定控制方案。此外，考虑到通常情况下速度信号会因为噪声等原因无法精确测量，因此，结合速度观测器对上述控制策略进行设计；同时，针对捕获过程产生的扰动项，设计了模糊控制滑模控制项以实现对其的补偿。上述结合柔顺装置给出的控制方案在有效实现吸收和缓冲捕获操作产生的冲击能量的同时，还能在冲击能量过大时适时开启或关闭关节电机，以避免关节电机发生过载与破坏。利用所提控制算法进行数值仿真，验证了上述避撞柔顺控制策略的正确性。

2 柔顺装置结构及避撞柔顺策略

配置柔顺装置空间机器人系统的机械臂关节由电机通过RSEA装置驱动，RSEA装置结构如图1所示。

在捕获阶段，机械臂末端与目标卫星发生接触和碰撞，并对关节处产生很大的冲击力矩，该力矩先作用在RSEA装置的扫臂上，然后通过扫臂将力矩传递到弹簧组上，通过弹簧组的变形将冲击能量存储在弹簧里，以实现对关节电机的保护。在镇定运动阶段，电机开启时也会受到冲击力矩，若所受力矩超过电机所能承受的极限而不关停电机，其将遭受过载或破坏。因此，需要根据关节电机所能承受的力矩极限设置一个关机力矩阈值使其关停。当检测到电机所受冲击力矩超过关机力矩阈值后电机关停，由于RSEA装置的存在，其内部弹簧组会提供弹力来减小关节所受的冲击力矩。为避免电机频繁开关机，进而影响电机性能，本文所提的避撞柔顺控制策略设置了两个力矩阈值，一个是电机关机力矩阈值，另一个是电机开机力矩阈值。当关节所受力矩超过关机力矩阈值时，电机关停；当关节所受力矩低于开机力矩阈值时，电机再次开启。

图1 RSEA装置结构

Fig.1 Structure of RSEA

3 动力学建模

以做平面运动的配置柔顺装置空间机器人系统捕获卫星操作过程为例，如图2所示，建立其动力学模型。

本文所用符号定义如下。假设系统载体的质量、转动惯量及其质心O0至O1的距离分别为m0，I0和L0；两机械臂的质量、转动惯量及两臂杆长度分别为mi，Ii和Li(i=1,2)；两关节电机转子转动惯量为Ii m；di为第i个关节转动铰中心到机械臂质心的距离；ki m为第i个RSEA装置中弹簧的刚度；θ0为载体姿态转动角，θi为机械臂关节转角，θi m为关节电机转子转角。系统总质心及载体、机械臂质心在惯性坐标系下位置矢量分别为rc,r0和ri；被捕获卫星的质量和转动惯量为ma和Ia。

根据图2中位置关系，可得捕获前空间机器人系统各分体质心的位置矢量表达式为

(1)

式中xb和yb为载体质心位置坐标；ei(i=0,1,2)为各连体坐标系xi(i=0,1,2)方向的基矢量。

对式(1)进行求导，可得系统总动能表达式为

(2)

式中ωi(i=0,1,2)为各分体相对于惯性坐标系的角速度，ωj m(j=1,2)为电机转子的角速度。

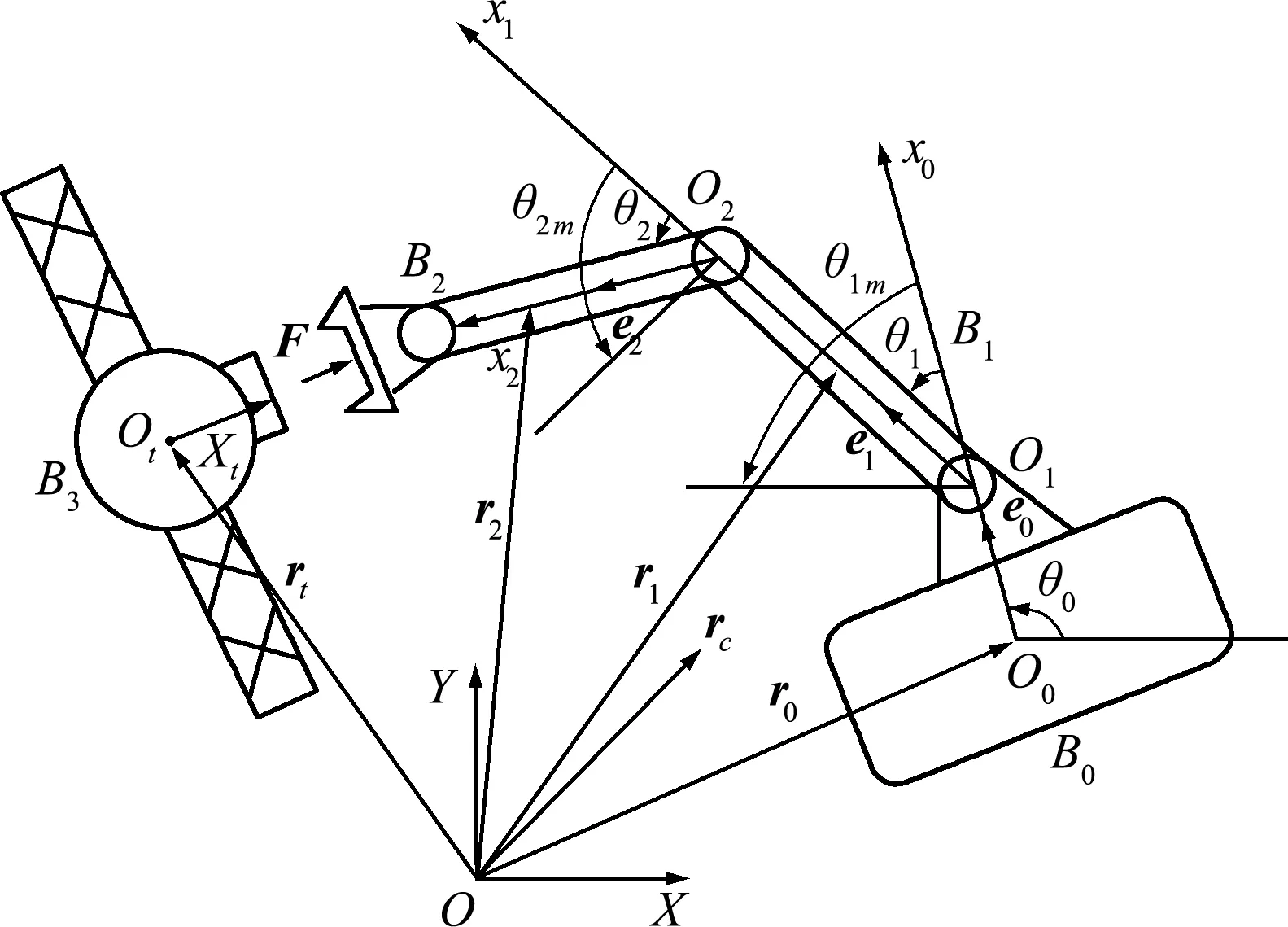
图2 含RSEA的空间机器人系统及目标卫星系统

Fig.2 Space robot with RSEA and target satellite system

不计太空重力影响，可知空间机器人系统势能只来源于RSEA装置，因而其总势能表达式为

(3)

式中Δxi L=x(αi)，Δxi R=-x(αi)分别表示其左右侧弹簧变形量，x(αi)=Rsin(αi)，αi为输入圆盘与扫臂之间的角度差。

基于上述动能和势能表达式，结合第二类拉格朗日方程，可得未发生捕获碰撞前载体位置不受控，姿态受控的空间机器人动力学模型为

(4)

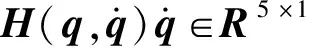
对于被捕获卫星，可将其视为均质刚体，则可通过牛顿-欧拉法获得其动力学模型：

(5)

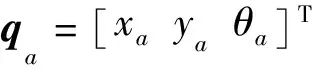
(6)

由于空间机器人系统进行捕获操作过程未受外力作用，整个系统满足动量守恒关系。结合动量守恒关系，对式(6)两端进行积分并整理得[12]

(7)

式中t0为发生接触碰撞的时刻，Δt为完成捕获所需时间，捕获完成后，两者形成混合体系统。

对于捕获完成后的混合体系统，空间机器人与卫星接触点满足速度约束，即自t0+Δt时刻满足：

(8)

结合式(7，8)，可得捕获碰撞对空间机器人运动状态的影响为

(9)

对式(4)第一项进行求导，并整理得

(10)

(11)

式中(JT)+1为JT的伪逆，且有(JT)+1=J(JTJ)-1。由于捕获碰撞时间极小，则碰撞力可以近似为

F=P/Δt

(12)

捕获操作完成后，空间机器人与目标卫星形成混合体系统，两者满足速度及位置约束关系，即式(8)恒成立，对式(8)求导，并整理得

(13)

结合式(4，6，13)，可得混合体系统综合系统动力学方程为

(14)

为延长空间机器人在轨服务年限，使载体位置处于不受控状态，式(14)为欠驱动形式。为将式(14)化为全驱动形式动力学方程，将其写成分块子矩阵形式：

(15)

(16)

式中

4 控制器设计

为实现捕获后失稳混合体系统的避撞柔顺控制，本文借助奇异摄动技术，推导出了等效刚度下的快慢变子系统模型。针对快变子系统提出了一种速度差值反馈控制器；针对慢变子系统设计了一种用于镇定运动的无源性模糊滑模控制方案，以实现避撞柔顺控制。

4.1 快变子系统控制器设计

考虑混合体系统针对快变子系统和慢变子系统分别进行控制方案设计，因此关节运动的总控制律可写为

τm=τs+τf

(17)

式中τs∈R2 × 1为慢变子系统控制力矩，τf∈R2 × 1为快变子系统控制力矩。

定义系统快变量为σ=K(θm-θ)。假设正比例因子ζ及正定对角矩阵K1，并令其满足：

K=K1/ζ2

(18)

结合式(18)及式(16)第2,3项，可得到描写系统弹性振动的快变子系统方程：

(19)

为实现系统弹性振动的主动抑制，设计如下速度差值反馈控制器对快变子系统进行控制，

(20)

式中Kf=K2/ζ，K2∈R2 × 2为正定对角阵。

将式(17，20)代入式(19)，可得

(21)

当ζ→0时，关节等效刚度K→∞，此时电机转子与臂杆之间可视为刚性连接，系统等效为刚性模型；则由式(16，17)得出慢变子系统动力学方程为

(22)

4.2 慢变子系统控制器设计

针对慢变子系统，其满足如下结构特性。

特性1MS θ和HS θ满足一致有界性，即有

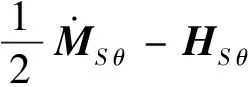
特性3HS θ满足互换可加性，即对于任意选取的x,y,z∈R3 × 1有

HS θ(qθ,x)y=HS θ(qθ,y)x

HS θ(qθ,z+ax)y=HS θ(qθ,z)y+aHS θ(qθ,x)y

考虑空间机器人捕获卫星的操作过程将产生有界扰动项τd，则慢变子方程(22)改写为

(23)

定义相关误差矢量为

(24)

式中qθ d为系统期望位置。

定义滑模切换函数：

(25)

式中λ=diag(λ1,λ2,λ3)(λ1，λ2，λ3>0)。

针对慢变子系统，设计如下形式控制器，

(26)

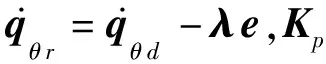
定义系统输出为y=s

选取Lyapunov函数

(27)

对式(27)进行求导，得到

(28)

将u+τd视为输入，则该系统满足传统无源性控制理论，因而输入u+τd到输出y是无源的。

考虑在实际控制中，速度信号因为噪声干扰等原因无法精确获得，因而针对式(26)中速度信号，可设计如下速度观测器对其进行动态估计，

(29)

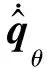
(30)

式中λ0为正定对称阵。对式(29)进行如下假设。

Kd,Kp 1和Kp 2为对称正定阵，且满足

Kd=kdI+λ0，Kp 2=kdλ0

(31)

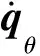
(32)

结合式(29)的速度观测器，控制器可重设为

(33)

联立式(22)及所设计速度观测器式(29)，可有

(34)

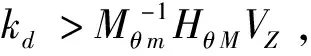
(t≥0)

(35)

式中Km=min.{Mθ m,Kp 1 m}，KM=min.{Mθ M,Kp 1M}，Kp 1 m和Kp 1M分别表征Kp 1的最小及最大特征值。

证明定义如下形式Lyapunov函数

(36)

对式(36)求导，可得

(37)

根据特性1和特性3及假设2，式(37)满足

(38)

根据设计的Lyapunov函数(36)，其满足

(39)

如果存在如下条件，

(40)

将式(40)代入式(38)，则存在γ>0，满足

(41)

由式(33)所设计控制器可知，为实现对捕获产生扰动下的稳定控制，采用滑模变结构控制项u以实现系统扰动项的补偿，其设计为

u=-dsgn(s)

(42)

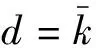
控制器(34)可改写为

(43)

dZ 0(s)+dN Z(s)=1

(44)

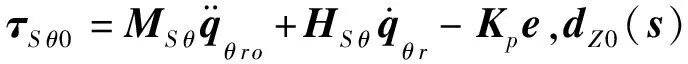
所设计模糊控制器，将实现以s为输入，dN Z为输出。设定三个模糊规则语言词集分别为{P,Z,N}={正,零,负}，每个模糊语言对应相应的隶属函数，输入输出隶属度函数如图3所示。同时，设计如下模糊推理规则

IF(sis N)then(dN Zis P)

IF(sis Z)then(dN Zis Z)

IF(sis P)then(dN Zis P)

由于在模糊推理中采用了Mamdani的最大最小合成法，因此采用面积重心法进行去模糊化处理。根据所设计控制器(43)，并结合适时开启和关闭关节电机策略，以实现系统的避撞柔顺控制。

5 仿真算例

5.1 捕获碰撞过程RSEA抗冲击性能模拟

K=2Km(3R2+r2)(2cos2φ-1)

(45)

式中Km=diag(k1m,k2m),R=0.1 m,r=0.01 m，φ为空间机械臂末端施加F=[20 N·m,20 N·m,0]T的载荷时扫臂的转角，仿真时选取φ=diag(3°,2°)。

为了验证RSEA装置在捕获碰撞过程的抗冲击性能，采用空间机器人对卫星进行捕获碰撞模拟，并计算关节所受冲击力矩，结果列入表1。

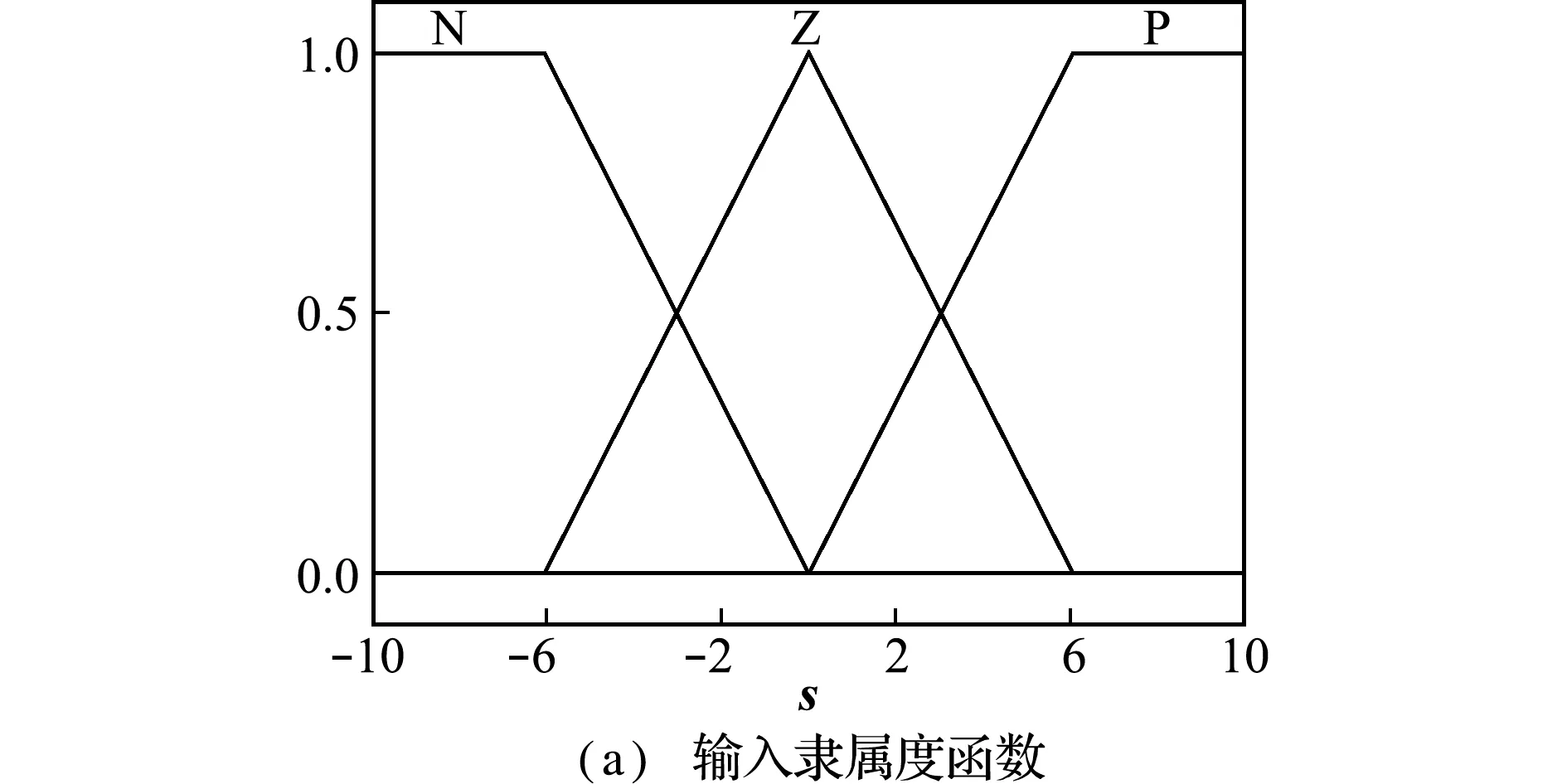
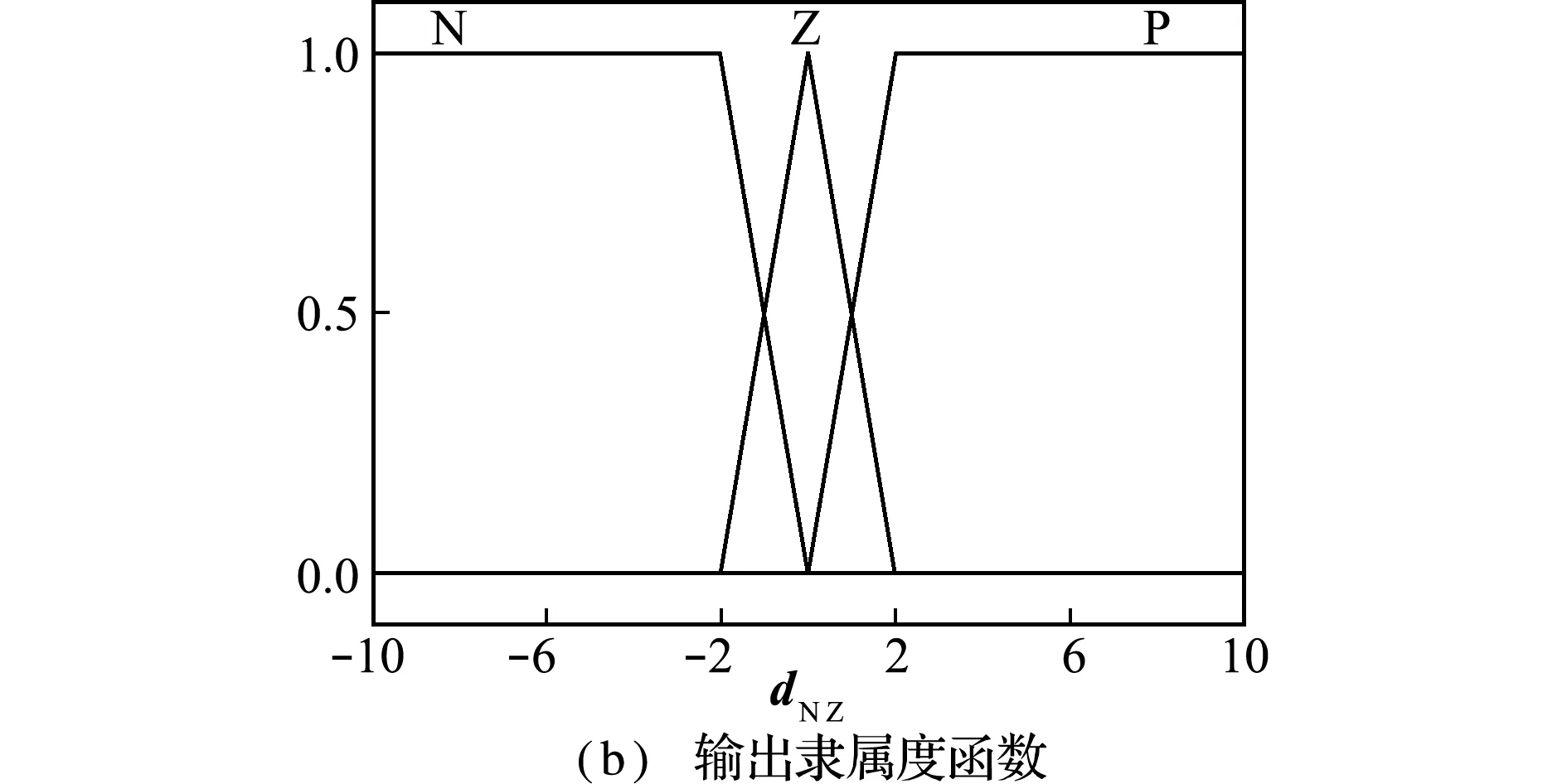
图3 输入输出隶属度函数

Fig.3 Membership function of input and output

表1 卫星不同初速度下RSEA的抗冲击性能模拟

Tab.1 RSEA impact resistance in different spacecraft initial velocities

卫星速度关节1所受冲击力矩关节2所受冲击力矩关节冲击力矩最大降低百分比[0.5,0.5,0]T[390.1,134.6]T[87.1,74.9]T65.5%[0,0.5,1]T[216.5,82.9]T[62.3,55.9]T61.7%[0.5,0.5,1]T[459.2,109.0]T[80.2,42.8]T76.3%

表1中，卫星速度前两项为线速度，单位为 m/s，第三项为角速度，单位为rad/s；关节1和关节2所受冲击力矩前后项分别为未配置与配置RSEA装置时，关节所受冲击力矩，其单位为 N·m。由表1可知，针对不同初速度卫星的捕获操作试验，配置RSEA装置较未配置RSEA装置，都能有效减小空间机器人关节电机所受碰撞冲击力矩，从而实现了对关节电机的保护。

5.2 捕获后镇定运动过程避撞柔顺控制性能模拟

图4为采用RSEA装置，但不开启适时开关机策略时的镇定控制情况。假设空间机器人关节电机所能承受冲击力矩阀值为70 N·m，由表1可知，此时关节所受冲击力矩虽小于未配置柔顺装置时的冲击力矩，但仍超过关节电机所能承受的极限。图5 为采用RSEA装置，并结合适时开关机的避撞柔顺策略的镇定控制情况，所选取关机阀值为48 N·m，开机阀值为6 N·m；通过对比图4和 图5 可以看出，此时关节所受冲击力矩限定在安全范围，实现了对关节电机的保护。图6为关节电机开关机情况。

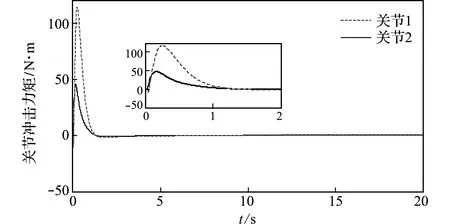
图4 未开启开关机策略关节所受冲击力矩

Fig.4 Joint impact torque without switching strategy

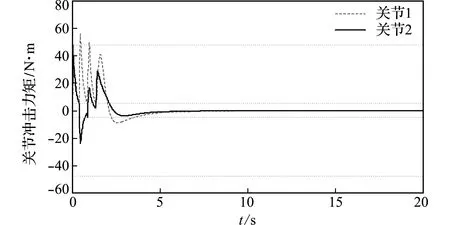
图5 开启开关机策略关节所受冲击力矩

Fig.5 Joint impact torque with switching strategy

图7为采用上述避撞柔顺控制策略时，载体姿态及关节轨迹镇定运动情况。可以看出，开启模糊控制较关闭模糊控制，可有效地消除抖振现象，且开启模糊控制的轨迹跟踪精度高于关闭时，进而保证了轨迹的精确跟踪。

图8为关闭所设计快变子控制器时，所得的轨迹跟踪情况。此时，因配置RSEA装置导致的关节柔性未得到抑制，关节产生弹性振动导致镇定运动难以实现。对比图7和图8可以看出，所提快变子控制律可实现系统弹性振动的主动抑制，进而实现捕获后镇定运动的稳定控制。

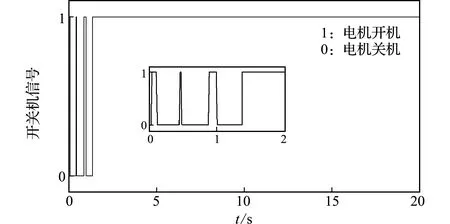
图6 开关机信号

Fig.6 Switch signal of joint motor

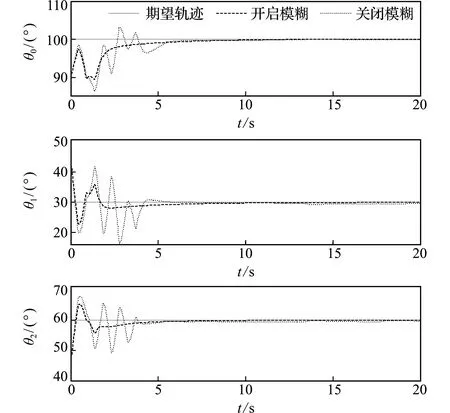
图7 镇定控制轨迹跟踪情况

Fig.7 Trajectory tracking of calm control

图8 镇定控制关闭快变子控制器轨迹跟踪情况

Fig.8 Trajectory tracking of calm control without fast controller

6 结 论

考虑空间机器人捕获操作的捕获阶段及镇定运动阶段，其机械臂关节处会受到巨大的冲击力矩的影响，为了保护捕获碰撞过程避免冲击力矩对关节电机造成破坏，本文设计了一种配置RSEA装置的空间机器人，并提出了一种与之配合的避撞柔顺控制策略。通过仿真试验可知，配置RSEA装置的空间机器人在捕获碰撞阶段最大可减小 76.3% 关节所受碰撞冲击力矩，最小也能减小 61.7% 关节所受碰撞冲击力矩，具有良好的抗冲击性能。而在镇定运动阶段，所提避撞柔顺模糊滑模控制策略确保了关节所受力矩限定在安全阀值内，保护关节电机不受冲击力矩破坏，并实现了捕获后混合体系统的镇定控制与轨迹的精确跟踪。