考虑主动时滞的汽车悬架系统控制特性研究

闫 盖，方明霞

(1.上海第二工业大学 工学部，上海 201209；2.同济大学 航空航天与力学学院，上海 200092)

1 引 言

悬架系统对汽车行驶平顺性和操纵稳定性具有重要影响，主动/半主动悬架可以有效抑制汽车振动，受到国内外学者的广泛关注。但悬架在控制过程中，由于信号采集、传输、控制器计算和作动器作动等因素，时滞不可避免。研究发现时滞对控制系统有较大影响，文献[1-3]发现，即使较小的时滞也可能导致系统控制失稳发散。文献[4-6]通过时滞补偿技术，一定程度上提高了系统控制效果。研究还发现，在控制中适当引入合理时滞，也可以改善系统的振动特性。文献[7]发现，时滞可以改变饱和控制的有效频带范围，将其作为控制参数可有效抑制系统振动；文献[8]在控制中引入主动时滞对水下机器人进行跟踪控制，结果显示对外部干扰具有较好的鲁棒性；文献[9,10]利用自适应控制策略设计了悬架时滞主动控制器，结果表明控制器具有良好的适应性和可靠性；文献[11]采用轴向时滞反馈控制策略对悬索进行振动控制，发现调节控制增益和时滞量大小可以避免共振区，有效抑制系统振动；文献[12]将时滞增益系数由定值变为时间的函数，以一定周期循环作用于减振过程，结果表明在时变时滞动力吸振器下，系统减振性能有了较大提高；文献[13]建立了含时滞状态反馈控制的四分之一悬架模型，通过matlab优化工具获得最佳反馈增益和时滞量，仿真结果表明，时滞反馈控制能有效提高车辆悬架的减振性能，改善车辆行驶平顺性；文献[14]将输出反馈控制应用于海洋钢套结构的振动控制，并在反馈中引入小时滞，不仅提高了减振效果，还降低了控制能量输出；文献[15]以简谐激励下吸振器主系统为研究对象，在计入固有时滞基础上引入主动时滞，讨论了反馈增益系数和主动时滞对系统减振特性的影响，结果显示，合理的主动时滞可以使动力吸振器具有更好的减振效果。

综上所述，目前对于含时滞悬架系统的研究已取得一定的成果，但主要是从时滞消除和时滞补偿技术角度进行研究，而对于测定悬架系统中的固有时滞量，并从时滞利用角度出发，在系统中引入主动时滞的理论和试验研究较少。为此，本文以2自由度DOF(Degree Of Freedom)汽车悬架系统为研究对象，采用理论和试验相结合的方法对考虑主动时滞的悬架系统控制特性进行研究，基于时域信号方法测定系统的固有时滞量，在控制中人为引入主动时滞，分析主动时滞对系统控制特性的影响，为时滞利用技术提供理论和实践依据。

2 含主动时滞的汽车悬架系统动力学模型

以1/4主动悬架为研究对象，建立2-DOF振动系统模型，不考虑系统状态时滞，只考虑系统控制中固有时滞和主动时滞的影响，其简化力学模型如图1所示。其中，固有时滞是由于主动悬架控制系统中信号的采集和传输、控制器运算及作动器响应延迟引起的时滞量，此时滞量在控制回路中不可避免；主动时滞是人为的在主动悬架控制回路中加入的时滞量，该时滞可以作为控制系统中改善性能的一个可调参数。

根据质点运动微分方程，得到含时滞悬架系统的动力学方程：

(1)

式中ms为簧载质量，mw为非簧载质量，ks和cs分别为悬架刚度和阻尼，kt和ct分别为轮胎刚度和阻尼，xs和xw分别为簧载质量和非簧载质量位移，u(t-τ-τa)为控制力，τ为悬架控制系统中的固有时滞，τa为控制中引入的主动时滞，xg为路面不平度。

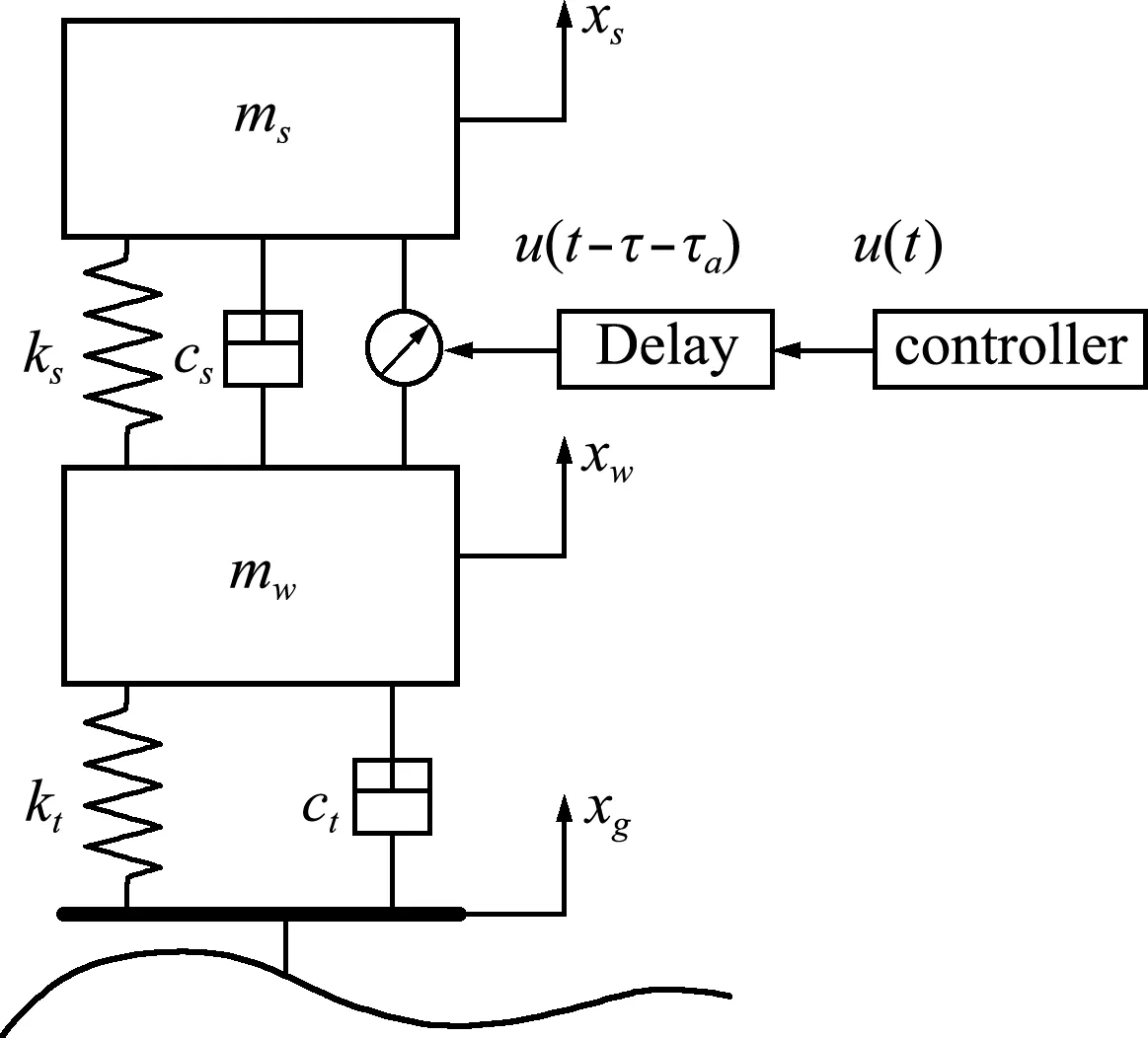
图1 悬架控制系统简化模型

Fig.1 Vehicle suspension model

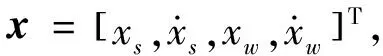
(2)

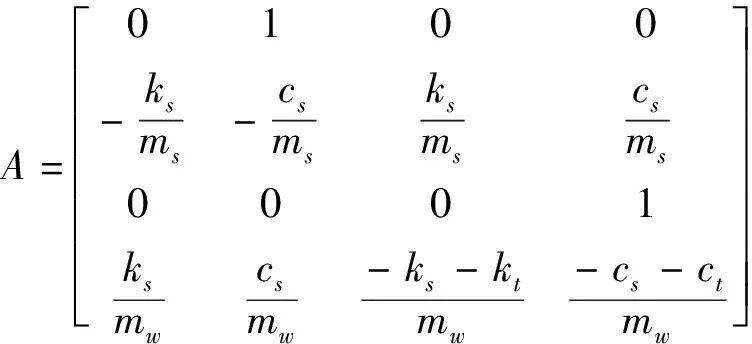
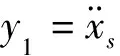
y=Cx+Du(t-τ-τa)+GW

(3)

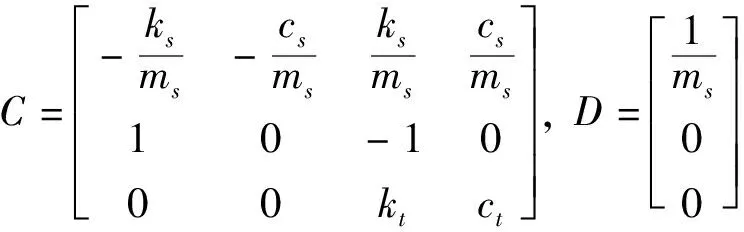
3 传统控制律研究含时滞悬架系统的稳定性

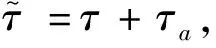
(4)

根据Routh-Hurwitz稳定性判据，实现系统稳定的条件是式(4)所有特征根均有负实部，因此系统失稳的临界条件是式(4)仅有纯虚根λ=iw，其中w是系统基频，将其代入式(4)，利用欧拉公式分离所得方程的实部和虚部，可得系统仅有纯虚根的条件为

(5)

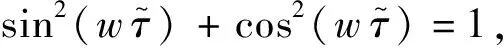
(6)

式中

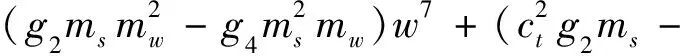
csg3msmw-g2ksmsmw+g4ksmsmw-

2g2ktmsmw+csctg2ms+csctg4ms)w5+

ctg1ksms+csg3ktms+ctg3ksms-

2csg1ktmw+g2ksktms-g4ksktms+

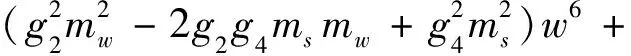
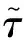
PA+ATP-PBR-1BTP+Q=0

(7)

式中Q=CTQ1C，Q1=diag[(q1,q2,q3)]，q1，q2和q3为控制系统输出权重；R=DTQ1D+R1，R1为正定加权矩阵。权重是根据对悬架性能要求倾向凭借经验确定，本文在确定权重时通过遗传算法对初始经验值进行了优化。

由式(6)及时滞稳定性切换判定定理，得到在传统二次型最优控制增益下，悬架系统的时滞稳定区间为[0，0.0143 s)。

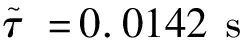
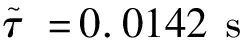
4 时滞主动控制律设计

现采用状态变换法[16,17]对含时滞的悬架振动系统控制律进行设计。针对状态方程(2)，采用如下状态变换。

(8)

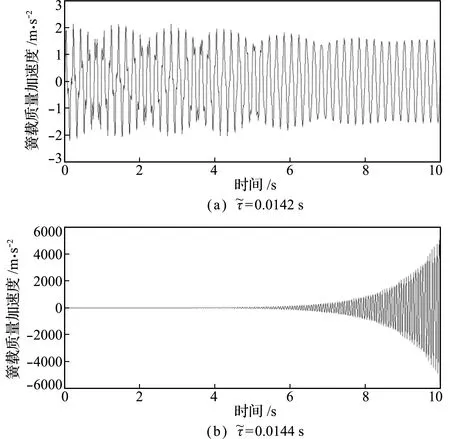
图2 传统二次型最优控制律下的簧载质量加速度响应

Fig.2 Sprung mass acceleration under the classical quadratic optimal control

则

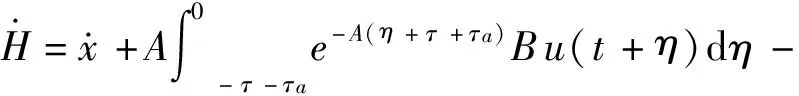
Bu(t-τ-τa)+Be-A(τ + τa)u(t)

(9)

将其代入方程(2)可得

(10)

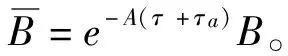
(11)

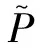
(12)

(13)

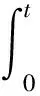
(14)

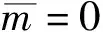
(15)

式中G(t)可通过式(16)进行迭代计算：

(16)

当t给定时，G(t)将于有限步趋于常数矩阵[18]。

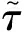
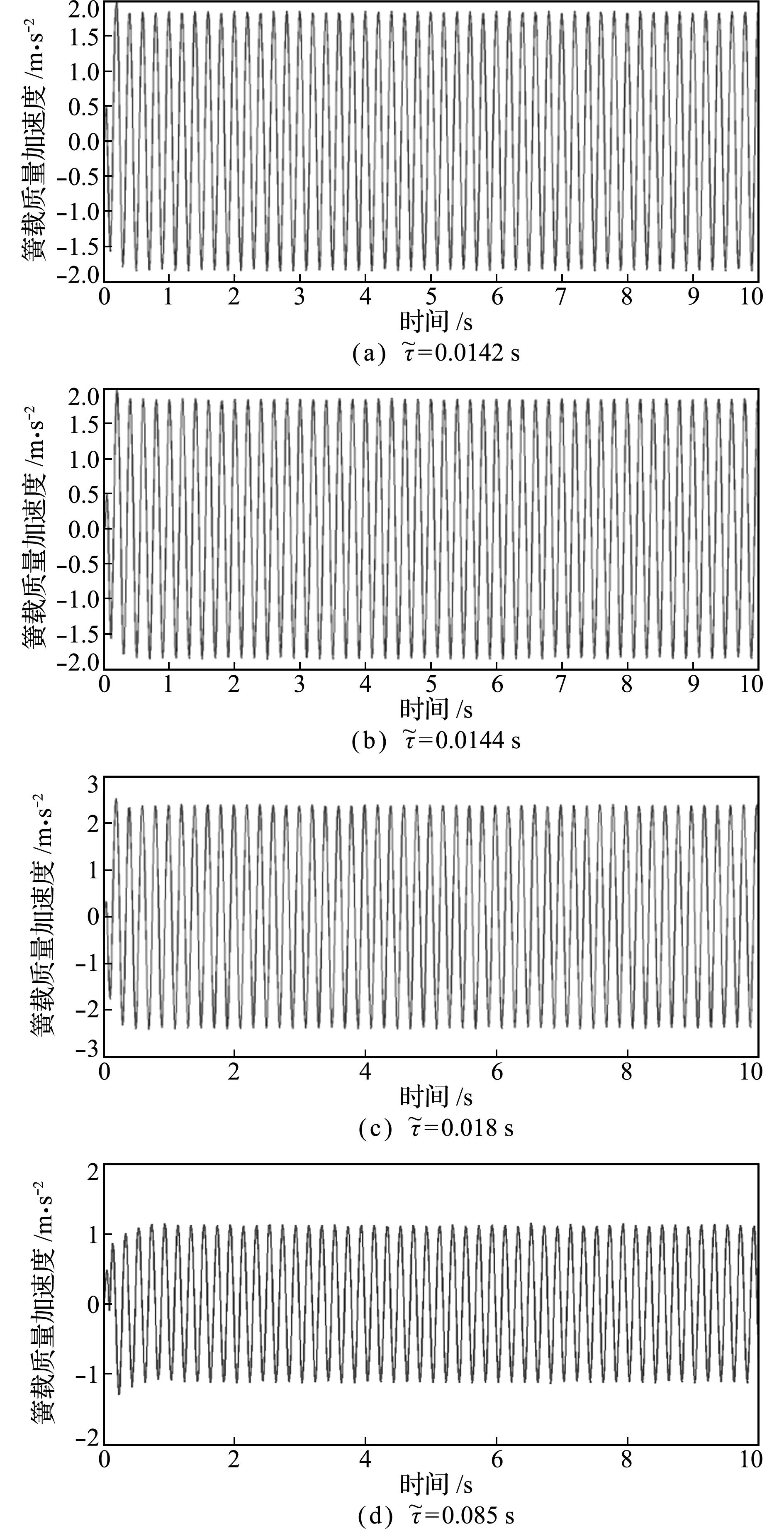
图3 时滞主动控制律下含时滞悬架系统簧载质量加速度

Fig.3 Sprung mass acceleration under the time-delayed optimal control with different time delay

(17)

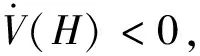
5 主动时滞对系统响应的影响及试验验证

5.1 悬架时滞主动控制理论分析

可以看出，与τa=0相比，τa=0.02 s，0.03 s和0.04 s时，簧载质量加速度幅值有一定降低，当τa=0.03 s时，降幅为57.7%；而当τa=0.01 s和 0.05 s 时，簧载质量加速度幅值有不同程度的增大，当τa=0.05 s时，增幅为76.1%。为了获得不同τa与加速度幅值之间的关系，现绘制加速度幅值随τa的变化曲线，如图5所示。可以看出，簧载质量加速度幅值与τa非线性相关，而是具有一定的周期性。当主动时滞τa=0.035 s时，簧载质量加速度取得最小值，比仅考虑固有时滞时降低了69.3%。因此，在控制过程中通过计算引入合理的主动时滞，可以大幅改善悬架系统的振动特性。

为了检验计算结果的有效性，现通过悬架时滞主动控制试验平台对分析结果进行验证。

5.2 悬架时滞主动控制试验

5.2.1 试验系统参数

以磁流变阻尼器为作动器，搭建了悬架时滞主动控制试验平台，试验系统如图6所示。

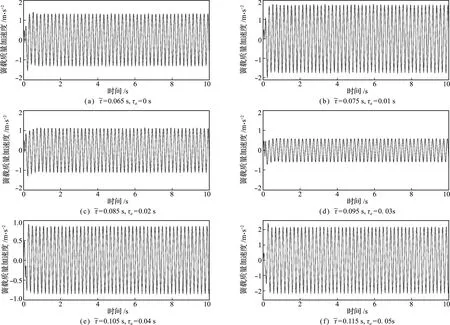
图4 主动时滞τa对簧载质量加速度响应的影响

Fig.4 Effect of active time delayτaon spring mass acceleration response

悬架试验系统经参数辨识，主要参数为ms=136.05 kg，mw=24.288 kg，ks=10200 N·m-1，kt=98000 N·m-1，ct=15 N·s·m-1，cs=153 N·s·m-1。系统中固有时滞τ=τ1+τ2，由两部分组成，τ1为信号从采集到输入磁流变阻尼器前的时滞量，τ2为磁流变阻尼器反应延迟。针对τ1，通过基于时域信号方法进行辨识，其辨识原理如图7所示，经过多次测量取平均得τ1≈0.037 s；根据文献[4]的磁流变阻尼器响应时滞辨识结果τ2≈0.0279 s。因此系统固有时滞τ≈0.065 s。

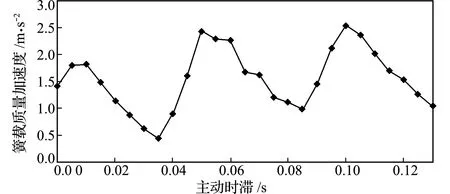
图5 簧载质量加速度幅值随τa的变化曲线

Fig.5 Relationship betweenτaand amplitude of spring mass acceleration

图6 悬架时滞主动试验平台

Fig.6 Photo of the experimental system

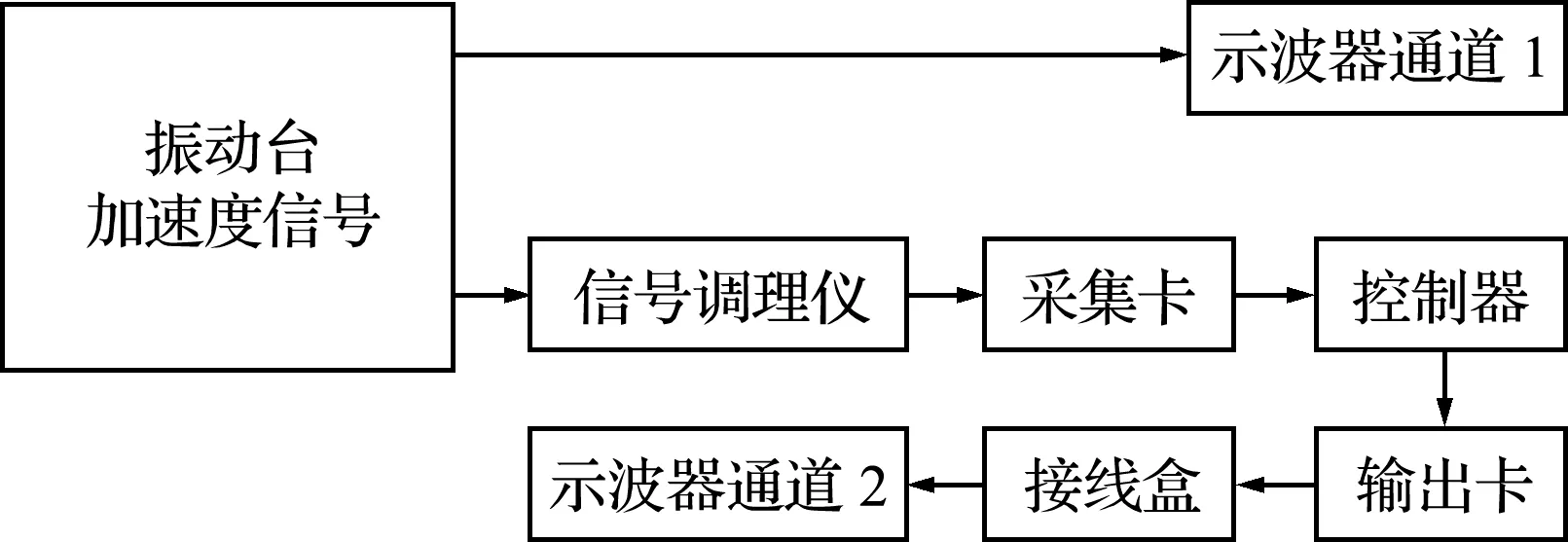
图7 时滞量τ1辨识原理

Fig.7 Principle of identificationτ1

试验中激励由振动控制器生成，通过功率放大器，由振动台将激励施加于模拟悬架装置。为了便于与仿真结果进行对比，试验中仍取简谐激励，振幅和频率与仿真计算的相同。

5.2.2 试验结果与理论结果对比

基于固有时滞τ≈0.065 s，采用状态变换法获得的悬架时滞系统主动控制律(11)，通过改变主动时滞τa对悬架系统进行试验。图8为不同主动时滞下簧载质量加速度的试验结果，为便于比较，同时给出了相同工况下簧载质量加速度的仿真结果。

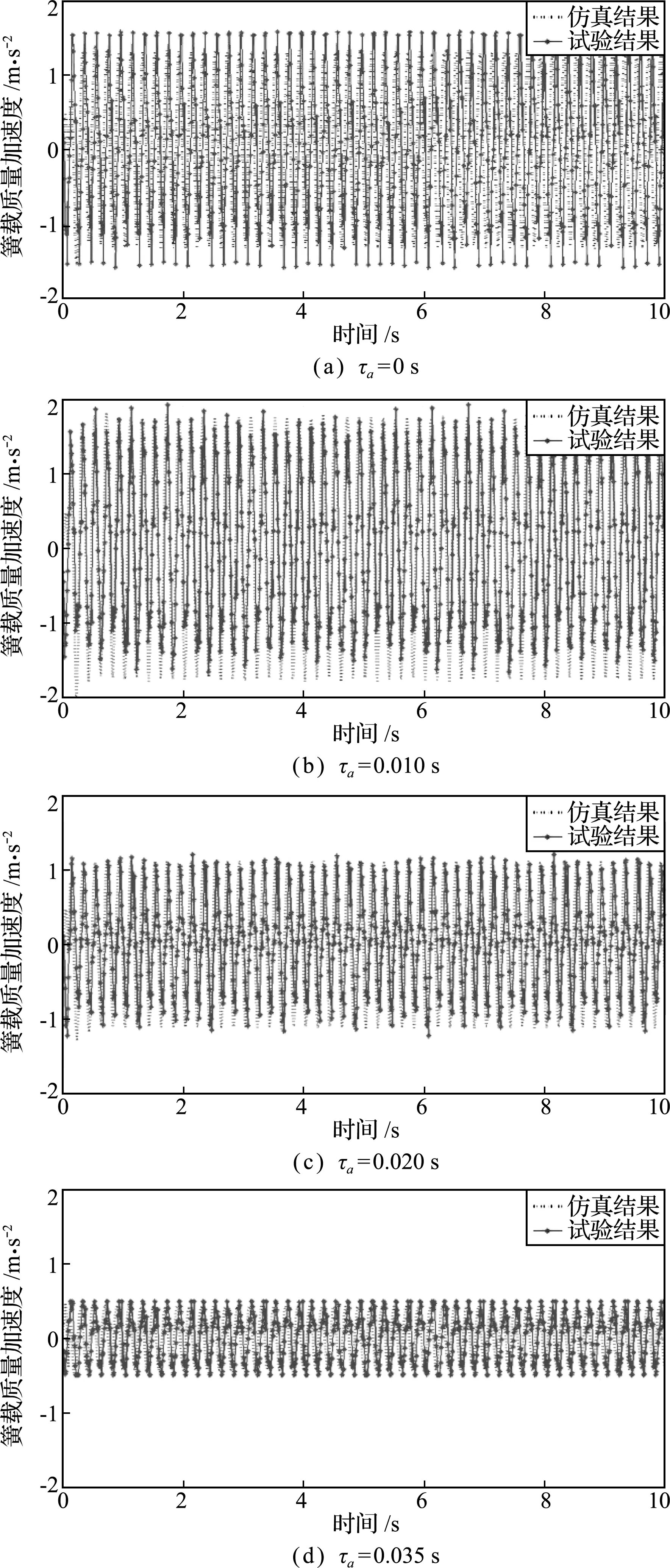
图8 不同主动时滞下簧载质量加速度

Fig.8 Spring mass acceleration with different active time delays

可以看出，试验结果与仿真结果具有较好的一致性，最大误差在15%以内，满足业内使用要求，说明采用状态变换法获得的主动控制律对含时滞的悬架系统进行主动控制具有较高的精度。

6 随机激励下悬架时滞主动控制

由于车辆实际行驶过程中受到的路面激励具有随机性，现采用前文获得的时滞系统主动控制律研究随机激励下悬架系统的动力学特性。

6.1 路面随机激励下悬架时滞主动控制模型

模拟路面随机激励的模型有多种，如正弦叠加模型、白噪声模型和功率谱模型等，本文采用基于滤波的白噪声路面不平度模型，即将路面不平度抽象为满足一定条件的白噪声，经变换后拟合出路面有色噪声随机激励模型，通过有理函数拟合可表示为

(18)

式中q(t)为车轮受到的路面随机激励，w(t)为白噪声，v为车辆行驶速度，α为路面相关系数，如A级路面α=0.09，B级路面α=0.1303，C级路面α=0.12，D级路面α=0.1007，E级路面α=0.09[19,20]。

6.2 随机激励下悬架时滞主动控制特性

悬架系统参数仍使用前文悬架缩尺模型参数，取B级路面，车速取20 m/s。通过计算，可获得系统在不同主动时滞τa下簧载质量加速度均方根值，列入表1。

表1 不同主动时滞τa下簧载质量加速度均方根值RMS

Tab.1 RMS of spring mass acceleration under different active time delays

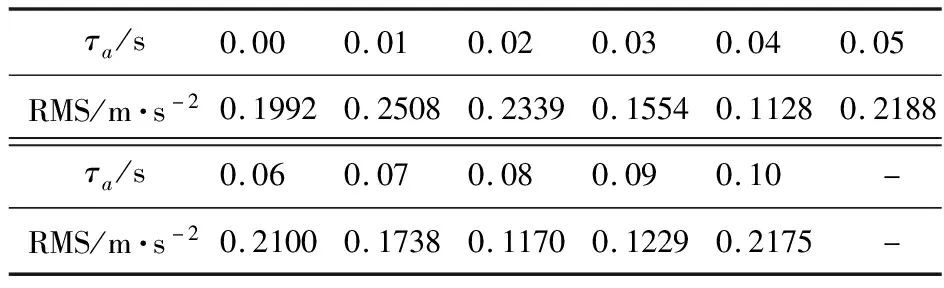
τa/s0.000.010.020.030.040.05RMS/m·s-20.19920.25080.23390.15540.11280.2188τa/s0.060.070.080.090.10 -RMS/m·s-20.21000.17380.11700.12290.2175 -

由表1可知，簧载质量加速度均方根值随主动时滞的变化而变化。当主动时滞τa=0.04 s时，簧载质量加速度均方根值为0.1128 m·s-2，比未引入主动时滞(τa=0.00 s)工况降低了43.4%；但当τa=0.01 s时，加速度均方根值高于未引入主动时滞工况。因此，通过计算获得合理的主动时滞，可以降低随机激励下汽车的振动幅值。

7 结 论

(1)以含时滞悬架系统为研究对象，采用常微分理论和多项式判定定理分析系统稳定性，理论和仿真结果表明，传统二次型最优控制下的系统稳定区间为[0,0.0143 s)，超出稳定区间后系统将失稳发散。

(2)基于状态变换法和最优控制理论设计了时滞主动控制律，该控制律可以保证系统全时滞稳定性。由簧载质量加速度幅值发现主动时滞可以使幅值下降60%，亦可使幅值增大超过70%，且两者不呈线性关系，具有一定的周期性。

(3)搭建了时滞控制试验平台对结果进行验证，在时滞主动控制下，系统中引入主动时滞 0.035 s，簧载质量加速度幅值比仅考虑固有时滞 0.065 s 时降低了69.3%，相同工况下的试验与仿真结果具有较好的一致性，表明研究具有较高的可信度。

(4)通过对路面随机激励下悬架时滞主动控制进行分析，发现在系统中引入主动时滞 0.04 s 时，簧载质量加速度均方根值比仅考虑固有时滞时降低了43.4%，表明研究结果对工程实际具有较好的适应性，为悬架时滞主动控制应用与研究提供了新的思路和方法。