10 的倍数分拆素数和的“1-9猜想”及思考

杨孝斌，黄晚桃，杨万鑫

（凯里学院，贵州凯里 556011）

1 问题的提出

在学习和研究哥德巴赫猜想的有关问题时，发现了一个关于10的倍数分拆为两个素数的和一个猜想：

10的正整数倍总可以分拆为个位分别为3和7的两个素数之和，即：对任意k∈N+，总存在素数p1,p2，且p1=10i+3,p2=10j+7,i∈N,j∈N，满足10k=p1+p2，并用C语言编程，利用计算机检验了20亿以内的10的倍数都满足猜想.［1］

为了区别后面的猜想，将上述猜想称之为10的倍数分拆素数和的“3-7猜想”.经过进一步的研究发现，如果将素数p1,p2令为p1=10i+1,p2=10j+9,i∈N+,j∈N+的形式，当3≤k≤20时，得到结果如表1所示.

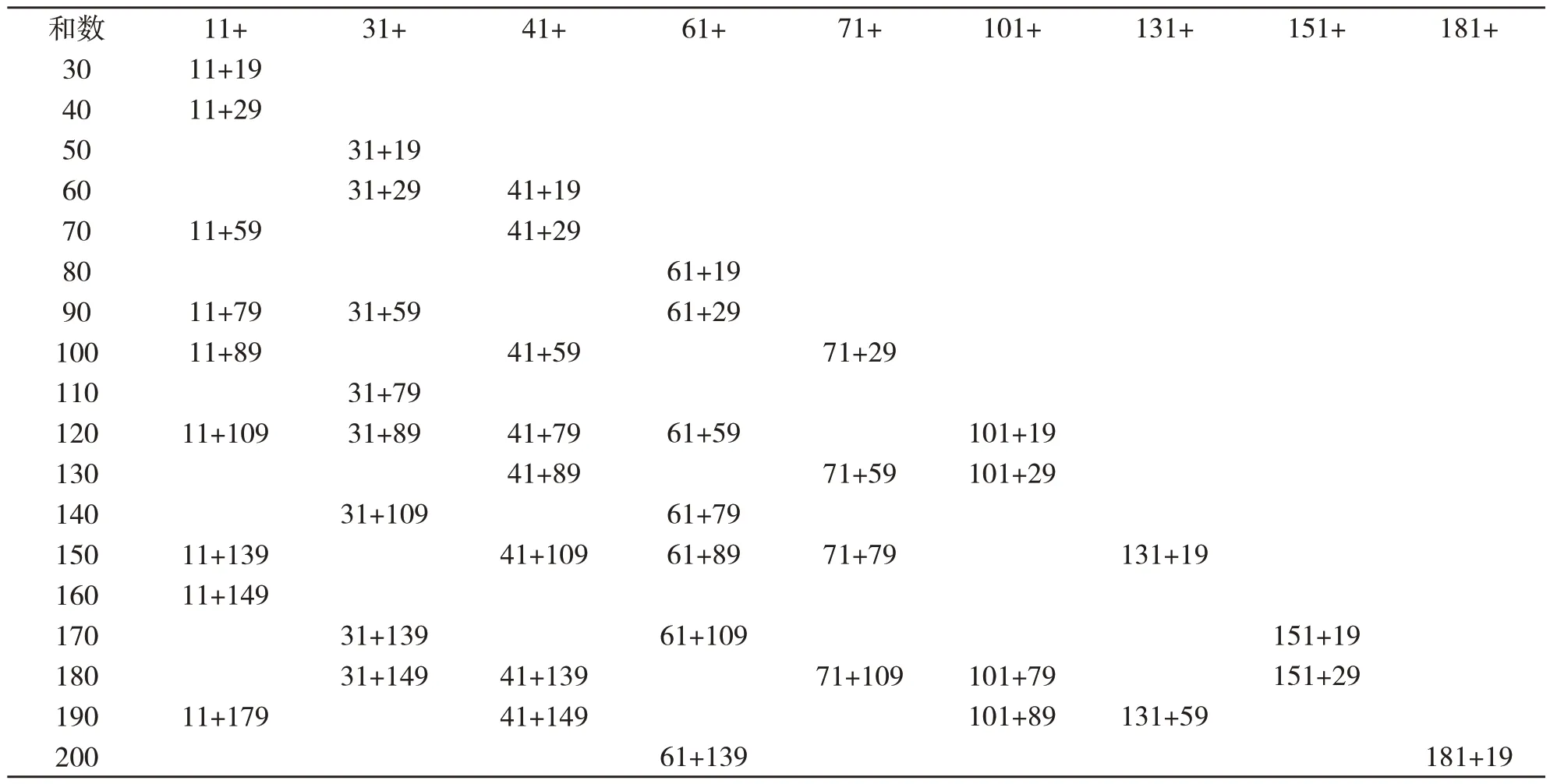
表1 10的倍数素数分拆的一些特例表

如果需要，可以将这个表列得足够长，在此基础上，提出如下猜想：

10的正整数（≥3）倍总可以分拆为个位分别为1和9的两个素数之和，即：对任意k≥3,k∈N+，总存在素数p1,p2，且p1=10i+1,p2=10j+9,i∈N+,j∈N+，满足10k=p1+p2（以下将此猜想称之为10的倍数分拆素数和的“1-9猜想”）.

为了进一步验证猜想的正确性（或找出反例），我们可以用C语言编程验证，程序类似于文［1］中的程序（整个程序时间复杂度为：o(n2)），只需把个位分别为3和7改为个位分别为1和9即可，在此不再赘述.

2 进一步的思考

结合10的倍数分拆素数和的“3-7”猜想和“1-9猜想”，在进一步思考的基础上，可以研究夹在10的倍数之间的那些偶数分拆素数和的情况.

仍然采用不完全归纳的思想，首先将30-100的偶数列表，如表2所示.

表2 任意偶数分拆素数和的一些特例

同样地，如果需要，可以将这个表列得足够长，在此基础上，进一步提出如下猜想：

对于每一个10k+d(k≥3,d=2,4,6,8)，存在10k+d=p1+p2，其中素数p1、p2均在10k与10(k+1)的分拆素数和中出现.

笔者尝试用C语言编程来验证，程序如下［1-2］：

注：整个程序时间复杂度为：O（n2）

3 结束语

经过计算机运行检验，上述10的倍数分拆素数和的“1-9猜想”以及“夹在10的倍数之间的偶数分拆素数和的猜想”在20亿以内没有反例.很显然，无论验证到多大的数，都不足以说明上述猜想是否一定成立，这需要从数学上进行严格的证明.上述猜想的证明与素数的分布密切相关，而且可能与著名的哥德巴赫猜想有关.笔者将进一步对其进行研究，也期待得到国内外各位同仁的帮助.