从信号博弈初探社会因素与语言结构的关联
2020-06-28唐丽萍
唐丽萍
1 引言
社会因素是否影响语言结构性质?如果是,有哪些社会因素以及从哪些方面体现?本文的目的是试图通过构建社会因素与语言结构的联系来解答这些问题。对这一联系的构建一直是社会语言学、认知科学及其他社会科学领域关注的问题,也取得了许多成果([2,8,10,12,17])。这些成果大多是通过田野调查、实验和统计的方法得到的。本文的创新点在于通过构建博弈模型来解答这一系列问题。相较于实验的方法,构建数学模型的优势在于,各种可能关联的社会因素和语言参数可以在数学建模中被有效地控制和调整,从而使得在这一模型下得到的关联性是更加稳定的。
语言结构是一个非常广泛的概念,我们不可能同时考察所有的语言性质。本文将集中考察语言中所谓的形态复杂性(morphological complexity)。衡量形态复杂性的一个重要标准是一个语言是否过分精确(over-specified)([1,11])。过分精确是相对于一定的语境来说的,因而形态复杂性也是一个相对的概念。我们通过一个例子来说明这一概念的涵义。亚古阿语是秘鲁亚古阿地区的人们使用的语言,这种语言具有相对高的形态复杂性。其动词词尾用五种表达不同距离程度的后缀变化来表达事件发生于一个小时前、一天前、一个星期前、一个月前和一年前。而英文中,通常通过加上一个时间短语来达到一样的表意。例如“我几天前摔断了腿”。从这一角度来说,亚古阿语是比英语更复杂的一种语言,因为在大部分情形下,使用一个动词时我们不需要知道该动作发生的时间距离。但亚古阿语并没有提供这样一种简单的选项。所以亚古阿语的动词表达就过分精确了。
从一方面来说,复杂语言能更精细地表意。另一方面,复杂性通常也会为语言使用者带来认知负担。而且在特定语境下,语言的精确是不必要的。简单歧义(ambiguous)等不精确表达已经能够有效的交流。例如:“很多人参加了昨天的讲座”中,很多情形下我们并不需要知道确切的人数,“很多”这样的不精确表达已经足够。同时,许多认知语言学的研究表明复杂表达造成更多的认知成本,简单表达是更经济的([3,7,20])。本文将在信号博弈的框架下,探究交流者在不同语境下对不同复杂度的表达的偏好。
在哲学和经济学中,刘易斯(D.Lewis)的信号博弈是研究语言交流的经典模型,最初是刘易斯为研究语义和习俗(convention)的形成而构建的([9])。许多研究语言性质的博弈模型都基于该信号博弈模型。例如:对语言概念空间的凸性([6])、含糊性(vagueness)([4])和语言的组合性(compositionality)([5])的研究。此外,基于信号博弈,还有研究语言歧义性优势的一系列工作([14,16])。这些工作着重关注词汇歧义(lexical ambiguity)的优势及其相对应的能够保持这种优势的博弈模型。本文所讨论的博弈模型能够在更一般的框架上刻画各种不同程度的语言复杂性,而对歧义性的探讨只是其中的一个特例。同时,本文更强调社会因素对会话者的语言复杂性偏好影响的探究。
本文着重考察的社会因素包括:群体结构比例、语言使用和学习成本以及社会经验(主要体现在会话者的知识背景)。为在模型中更好地同时融合这些参数,我们应用复制动态(replicate dynamics)这一数学技术。在进化博弈论中,复制动态既是一个均衡优化的方法,也是一个考察群体动态变化的有效研究机制([13,15,18,21])。因而本文会在信号博弈的基础上,结合复制动态的研究方法,从而在静态博弈和动态博弈两个维度上对社会因素与语言结构的关联进行更全面的考察。
在刘易斯的信号博弈的基础上,我们做了两个主要的扩展。第一个扩展是加入一个具有复杂度的信号结构,使得该信号博弈模型可以被用来探讨语言的不同复杂度。第二个扩展是引入会话者的背景知识,也可以看作是会话语境。在这两个扩展的基础上,考察静态和动态两个信号博弈模型,并同时讨论语言使用成本、群体结构以及会话者的背景知识等社会因素如何影响会话者对于语言复杂度的偏好。
文章结构安排如下:第2 节简单介绍刘易斯的信号博弈及其基本概念。第3 节中,我们首先定义一个复杂信号结构并在此基础上讨论该形式语言的复杂度,然后给出基于复杂信号结构的信号博弈。第4 节讨论群体内的语言复杂度偏好。第5 节我们讨论跨群体的语言复杂度偏好。最后我们将本文模型与文献中已有的相关工作进行比较和讨论。
2 刘易斯信号博弈模型
为了从社会约定(convention)的维度来建构语言的意义,刘易斯在1969年建构了信号博弈。该信号博弈中,有两个会话者,发信者和收信者进行信息交流的互动。在交流过程中,只有发信者对信息进行观察,然后发送信号给收信者传递信息。收信者收到信号后,采取相应的行动,行动的结果决定两者的收益。形式上该博弈定义如下。
定义1.一个刘易斯信号博弈G={N,{S,R},S,A,U}是一个多元组,其中,
•N={1,2,...,n}是一个世界状态集;
•{S,R}指该博弈的主体为一个发信者S和一个收信者R;
•S={s1,s2,...,sn}是一个有穷信号集;
•A={a1,a2,...,an}是一个有穷行动集;
•U为收益函数,定义为U(i,aj)=1,当i=j;否则U(i,aj)=0,其中i ∈N,aj ∈A。
发信者的策略是从世界状态集到信号集的函数,收信者的策略是从信号集到行动集的函数。
最简单的刘易斯信号博弈包括两个世界状态,两个信号和两个行动。例如:N={1,2},S={s1,s2},A={a1,a2},U(1,a1)=1,U(1,a2)=0,U(2,a2)=1,U(2,a1)=0。
在这一类信号博弈中,有三种不同类型的博弈均衡。
• 第一种是分离均衡(separating equilibrium)。这种均衡下,世界状态、信号和行动一一对应。上述例子中的分离均衡为
其中,世界状态1 发生时,发信者发送信号s1,收到s1后,收信者采取行动a1。同样地,世界状态2 发生时,发信者发送信号s2,收到s2后,收信者采取行动a2。在这样的均衡策略下,博弈者能够准确地交流信息。信号s1和s2也被分别赋予了世界状态1 和世界状态2 的意义(meaning)。我们也可以用在世界状态集上的划分{1|2}来表达这一语义。该划分有两个元素{1}和{2},分别对应于两个信号s1和s2并赋予其意义。例如信号s1的意义为“世界状态1 发生”。
• 第二种均衡是汇合均衡(pooling equilibrium)。汇合均衡中,同一个信号同时表达不同的事件。因而有歧义信号的存在,导致交流中存在不确定性。例如:
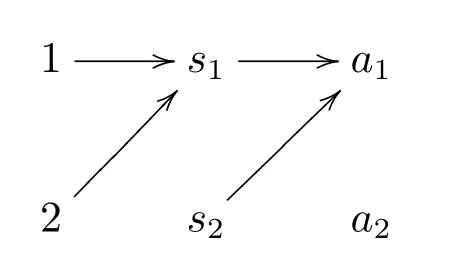
发信者在两个世界状态下都发送信号s1,而收信者则无视发信者的信号,只采取行动a1。在这个均衡下,交流者并没有成功地交流信息。与此均衡相对应的意义划分为{1,2},也就是一个信号被用来表达两个世界状态。这样的信号被称为带有歧义性(ambiguity)的信号。
• 第三种均衡是部分汇合均衡(partial pooling equilibrium)。若将上述例子扩展为三个世界状态,三个信号及三个行动。我们可以得到如下的部分汇合均衡。
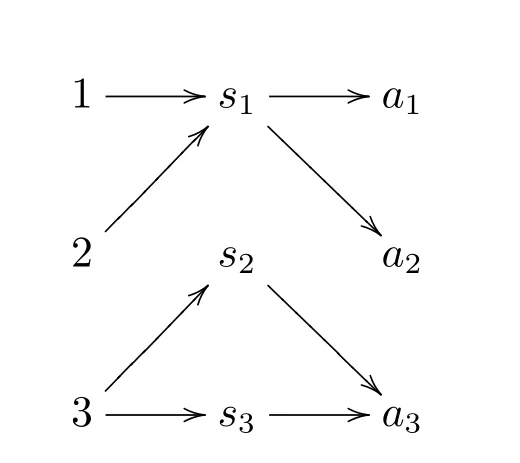
在这一均衡下,有精确信号也有歧义信号,因而只有部分信息能有效传递。与之相对应的意义划分为{1,2|3},其中世界状态1 和2 无法被区分,但世界状态3 能够被准确传递。该划分所对应的信号及其意义为:
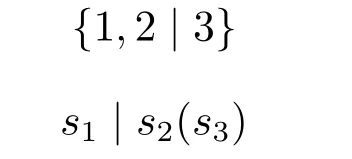
我们称每个信号均衡为一个信号结构。在刘易斯信号博弈中,一个博弈模型中只有一个信号结构。也就是说,不能对一个信号集同时进行多个意义建构。例如,s1不能既表达“世界状态1”,又表达“世界状态1 或世界状态2”。
我们将对刘易斯信号博弈模型做两个扩展,第一个扩展是在新的博弈模型中,同时考察多个信号结构,而且这些信号结构具有不同的复杂度。第二个扩展是假设博弈中的会话者具有不同的背景知识,这一背景知识也可以当作交流的语境。
在给出新博弈模型的准确定义前,我们先来讨论什么是复杂信号结构。
3 复杂信号结构及复杂信号结构博弈
3.1 复杂信号结构
刘易斯的信号博弈中,信号的意义是从外部给出的(通过定义博弈的纳什均衡),作为博弈者,他们对于信号的意义是没有自觉的。这是因为刘易斯建构信号博弈模型的初衷是探讨语言意义的形成机制,从而博弈者在语言使用之初,对于语言的意义可以不自知。但在日常语言交流中,交流者对于语言的意义通常都是有预设的。所以在新的模型中,我们首先将在模型内部给定信号的意义。同时,为了探讨各个信号结构的相对复杂度,初始模型中也会同时定义多个信号结构。从这两点出发,我们首先来定义一个复杂信号结构。
定义2.给定一个有穷世界状态集N,一个复杂信号结构SP={P,Sij,C}是一个三元组,其中:
• P∈P(PN),PN是定义在N上的所有划分的集合,P(PN)定义为PN所有子集的集合。P 中的元素,也就是N上的一个划分用Pi来表示,我们称之为一个信号结构,其中Pi中的元素用{Pi1,Pi2,...,Pii}来表示,i为该划分中的元素个数。1通常地,具有相同元素个数的划分可以有多个,为避免混淆,我们假定P 中不存在具有相同元素个数的划分。直观上来说,具有相同元素个数的划分在我们的模型中被认为具有相同的复杂度,从而可以由此定义一个等价类。因而考虑其中一个已经可以满足我们对复杂度讨论的要求。
• 对于每一个Pi ∈P,Pi中的每一个元素Pij对应于一个信号sij,同时信号sij的意义由Pij所对应的世界状态给出。由于划分中可以存在多元素的集合,所以某个信号的含义也可能是不确定的,这个时候我们说该信号是歧义的(ambiguity)。
•C >0 为每个信号的成本。2出于模型的简单性考虑,本文假设对同一个主体来说,不同信号的成本是相同的。对这一假定的改变会影响本文的结论。在未来的工作中,我们可以尝试放宽这一假定。
由定义2 可以给出信号结构复杂度的定义。
定义3.给定一个复杂信号结构SP,给定Pi ∈P,定义Pi的复杂度为iC,用来表示。iC越大,复杂度越高。
复杂度的定义符合我们对于复杂度的直观理解。一个语言复杂度的衡量标准是该语言是否过分精确,过于精确的语言被认为是复杂的。在我们的定义中,实质决定复杂度的是参数i也就是一个信号结构中的元素个数。一个信号结构相对应的信号个数越多,表明该信号结构越精确,所以复杂性也就越高。而复杂度低的信号结构中,由于信号个数的减少,那就意味着同一信号可能需要表达更多的世界状态,也就是歧义性的信号会赠多。因而复杂度低的信号结构不确定性也大。不同的信号结构可以看成是表达同一事物的不同维度,例如颜色,形状,时间等等。下面我们用一个例子来说明定义2 和定义3。
例1.给定一个事件状态集N:{1,2,3,4},P={P2,P3},其中3我们用符号“ | ”来区分信号结构划分中的各个元素。,

各个信号结构的组成元素为{P21,P22,P31,P32,P33},其所对应的信号集为{s21,s22,s31,s32,s33},信号的意义由其所对应的划分元素中的世界状态决定。例如,s22的含义为“世界状态2 或者世界状态3 或者世界状态4”。P2的信号复杂度为2C,P3的信号复杂度为3C。因而相对于P2来说,P3更复杂。同时P3的表达也更加精确。
3.2 复杂信号结构博弈
本节中,我们将定义一个基于复杂信号结构的信号博弈。同时,我们将博弈者的背景知识加入到我们的新模型中。形式上,我们用世界状态上的信息划分(information partition)来表达背景知识的概念。为了区分信号结构和博弈者的信息划分,我们用符号∥来区分信息划分中的不同元素。相较于传统信号博弈来说,复杂信号结构博弈加入了一个新的步骤。收信者在受到发信者发出的信号后,他将结合信号所携带的信息以及他自己的背景知识。经过简单推理后,采取相应的行动。我们可以定义复杂信号结构博弈如下:
定义4.一个复杂信号结构博弈G={N,{S,R},SP,I,A,U}是一个多元组,其中:
• 一个有穷世界状态集N,假定每个事件发生的概率ρ是一样的;
• 两个博弈者:发信者S,收信者R;
•SP为一个复杂信号结构;
• 每个博弈者有一个表达其个人背景知识的信息划分I,I定义为世界状态集N上的一个划分;4本文所涉及的博弈中,博弈者的背景知识与所交流信息不存在矛盾。存在矛盾的情形可以作为未来模型扩张的一个方向。
• 一个行动集A=P(A),其中A={a1,a2...,an},P(A)为A的子集的集合。由于歧义信号的存在,收信者的行动可能是一个集合α ∈A;
•U为收益函数,定义为,ai ∈αi,其中|αi|为集合αi中的元素的个数。
在这个新的博弈模型下,博弈者进行如下的博弈:某个世界状态随机产生,发信者收到世界状态的信息,从复杂信号结构中选取一个信号来发送。收信者收到信号后,结合其自身的背景知识信息,从而决定要采取的行动。该行动决定博弈双方的收益。这里有两点需要强调:
1.在这一博弈中,我们只考虑收信者的背景信息。因为博弈者的收益完全由收信者的行为来决定,发信者的背景知识不发生作用。而且信号是不影响收益函数的,所以信号博弈也被称为廉价交谈博弈(cheap talk game)。当发信者与收信者交换身份后,也就是发信者作为收信者后,其背景知识就会发生作用。
2.在复杂信号结构下,发信者的策略还没有被确定,因为当某一个世界状态发生时,有若干个信号都是可以表达同一含义的。例如在例1 中,当世界状态2 发生时,信号s12和s31都可以部分表达这一信息。那么,哪一个信号更好?这与收信者的背景知识,以及同一信号结构中的其他信号的优劣有关。所以我们将在复杂信号结构博弈的基础上,来比较各个信号结构的优劣。我们假定一个信号结构的优劣可以决定其每一个信号在该博弈中的优劣。
一个信号结构的优劣是通过反复进行的复杂信号结构博弈来得到的。我们计算每一个信号结构在每一个世界状态发生时的收益,并对其进行平均值的计算。形式上来说,就是计算Pk的期望效用。我们用如下定义的期望效用EPk >0 来评价信号结构Pk。
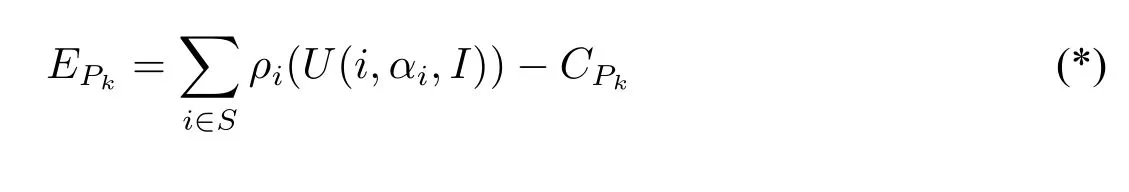
其中,ρi为事件i发生的概率(假设其均匀分布)。CPk为信号结构Pk的复杂度。U(i,ai,I)为在收信者的背景知识I和行动αi下的双方的收益。博弈者对于信号结构的偏好由来决定:效用大的信号结构优先。从而,当发信者面对来自不同信号结构的同时可以表达(或部分表达)某一世界状态时,来自更优的信号结构的信号优先。
我们用以下的例子来更直观地阐述相关概念。
例2.
•一个世界状态集N:{1,2,3,4};
•一个信号结构集如下:

•收信者的信息划分I:{1,2,3|4}
• Cs和Cr为发信者(发送)和收信者(接收)的信号成本。
•一个行动集合P(A),其中A={a1,a2,a3,a4}。每个信号结构的效用可以用公式(*)来计算。例如,当事件2 发生时,我们来计算信号结构P2的效用。发信者从信号结构P2中选择表达世界状态2 涵义的信号。该信号为歧义信号,其表达的涵义为状态2 或3 或4。同时收信者根据自己的背景知识得知,发生的世界状态为为状态1 或2 或3。当收信者将接收到的信号信息和自身背景知识相结合后,推论得出发生的状态为世界状态2 或3。因而,收信者将采取行动a2或a3。所以当事件2 发生时,由于行动集是包含两个元素的不确定集,所以收益为。当其他事件发生时,可以用同样的方法来计算收益。同时,P2对应的信号数为2,所以信号成本为2C。因此,P2的效用为:

其他信号结构的效用也可以用同样的方法计算得出。
基于以上定义的复杂信号结构博弈,我们可以讨论博弈者对不同复杂度信号结构间的偏好以及该偏好形成背后的理由。
4 群体内交流的语言复杂性偏好
利用已定义的复杂信号结构博弈,我们可以讨论不同群体对语言复杂性的偏好。不同群体可以用不同的知识背景来区分。我们考虑两个具有不同认知状态的群体。一个群体拥有关于所交流信息的背景知识而另一个没有相关背景知识。假设没有背景知识的为群体一,具有一定背景知识的为群体二。首先,我们考察群体内交流时,博弈者对语言复杂性的偏好。我们用例子来说明回答这一问题的基本思路。
例3.(群体一)
•一个世界状态集N:{1,2,3,4};
•一个带有不同复杂度的信号结构集如下:

•收信者的信息划分I:{1,2,3,4};5该划分只包含一个元素,说明主体对于交流内容相较于世界状态集本身没有更多的信息。
• C为信号成本。
为比较博弈者对于不同复杂度信号结构的偏好,我们计算各个信号结构的效用如下:

假设Ei >0,i=1,2,3,4,则。通过简单计算比较,为最优信号结构。也就是说,给定一个复杂信号结构博弈G,对于没有额外背景知识的群体一,复杂但更精确的信号结构为最优选择。
例4.(群体二)
保留例3 中的所有假定,唯一不同的是,群体二有额外的背景知识I:{1,2,3∥4}。在这一假设下,每次收信者在作出行动之前,将会结合信号信息以及自身的背景知识来做出行动选择。同样,我们可以根据(*)来计算各个信号结构的效用如下:

假设Ei >0,i=1,2,3,4,则。显然为最优信号结构。因此,在具有背景知识的群体二内,相对简单的信号结构是更优的选择。
沿用这两个具体例子中的基本思路,我们可以得到以下两个一般结论。
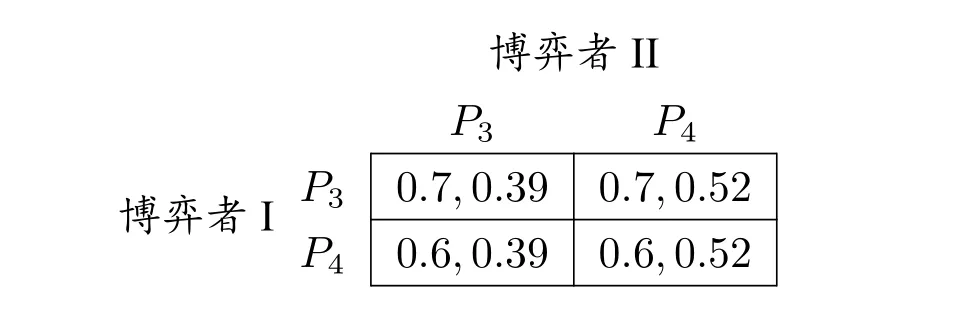
命题1.给定复杂信号结构博弈G,假设其中N={1,2,...,n},并且I=N,那么EPn >EPm,其中m 证明.利用(*),可以容易计算Pn的效用是。 假设任意信号结构Pk(k 假设EPn >0,则。显然,Pi随着k的增加而变大。所以Pn为最优选择。 命题1 说明,在我们定义的博弈模型下,当一个群体没有额外相关知识的时候,交流者偏好复杂但能精确表达的语言。这一结论也是符合直观的,当交流者双方对彼此和对所交流的内容完全无知时,为了更有效地交流信息,他们只能通过语言来表达尽可能多的信息。 当博弈者具有一定背景知识时,很难获得一个类似于命题1 一样的一般性结论。因为对于不同的背景知识,结论可能完全不同。但我们可以得到一个较弱的一般性结论。 命题2.给定复杂信号结构博弈G,其中,如果存在一个信号结构Pk,0 证明.显然EPn=1−nC。因为k 由命题2 可知,当交流者具有相应的背景知识时,他们所使用的语言有可能倾向于较简单的表达。这一结论在自然语言交流中,也是非常直观的。当交流着双方对所讨论的话题足够了解时,简单的语言就能有效地交流。例如,当两个老朋友在谈论接下来的安排时,其中一人说“I am going to the bank”。其中一人会自然地将bank 理解为银行还不是河边,因为他知道对方最近正在办借款买房。而bank 是一个带有歧义性的词。 在这一节中,我们证明了当群体具有相应的背景知识时,交流时使用的语言可能会更愿意使用相对简单的语言。而当群体对所交流话题没有任何相关信息时,交流者偏向于使用更精确但复杂的表达。 命题1 和命题2 都假定了博弈者只在群体内部交流。当博弈者可以跨群体交流时,博弈状态会更为复杂。我将在下一节中讨论跨群体交流的情形。 这一节中,我们考察在一个复杂信号结构博弈中,博弈者可以来自两个不同群体,也就是说博弈者有不同的知识背景。在上一节中,我们已经考察了同一知识背景的群体在交流时对于不同复杂度的信号结构的偏好。当考虑跨群体(具有不同知识背景)交流时,我们可以从不同的角度来构造博弈。为了延续前文的讨论,我们在前文的例子上构建一个较为简单直接的跨群体博弈。 例5. •一个世界状态集N:{1,2,3,4}; •两个博弈者,博弈者I(群体一代表),博弈者II(群体二代表); •复杂信号结构如下: •博弈者I 的知识背景为I:{1,2,3,4};博弈者II 的知识背景为I:{1,2,3∥4}; • Ci为博弈者i的信号成本,i=I,II。 该博弈过程如下: 当分别来自群体一和群体二的博弈者I 和博弈者II 相遇时,他们会交流两次。一次博弈者I 为发信者,博弈者II 为收信者;另一次为博弈者II 为发信者,博弈者I 为收信者。假设只有当博弈者作为发信人时,才获得收益。为了说明的简洁,假定发信者的策略为选择信号结构而不是直接选择信号(由于信号的意义是确定的,所以选择了信号结构相当于确定了信号,所以两者可以通用)。收益矩阵可以由表1 来说明。每个表格内的第一个数值为博弈者I 的收益,第二个数值为博弈者II 的收益。收益为信号结构P3和P4的期望效用,我们用之前定义的公式计算得到。例如,当博弈者I 为发信人,当其选择信号结构P3时,他的收益由作为收信人的博弈者II 的行动决定。所以通过前文的例4 可得,其收益为1−3C,而发信人为博弈者I,因而其信号成本为CI,所以博弈者I 的最终收益为1−3CI。表1 中其余相对应的数值可由相同方法分析得出。 表1:跨群体博弈收益 这个博弈中,(P3,P4)为纳什均衡。6从对例3,例4 的讨论得出,CI <,CII <。通过简单分析,可以得到(P3,P4)为纳什均衡。该博弈的有趣点在于,当博弈者I 为发信者时,他可以利用博弈者II 具有较多背景知识这一特点。也就是说,当他遇到博弈者II 作为收信人时,即使发送较简单的信号P3也可以精确交流所有事件信息。而对于博弈者II 来说,他就没有这种优势。因为当他遇到博弈者I 作为收信人时,复杂信号P4为更好的选择。而当他遇到群体内的博弈者时,由例4 可知,他的优势策略为相对简单的P3,且能获得更好的收益。 下面我们研究如此定义的跨群体博弈中,不同群体的表现及其对语言复杂度的偏好。我们考察信号成本相同及不同两种情况。 我们用进化信号博弈中的复制动态来考察群体在博弈中的表现。在进化信号博弈中,复制动态是一种细化均衡同时也是一种稳定性分析的方法。它被用来分析群体中策略的动态变化。其主要思想是,当一个策略的收益超过所有策略的平均收益时,该策略就会获得进化优势。复制动态系统可以用以下公式来表达。 其中qi是策略i的比例,t表示时间序列,Ei是策略i的期望收益,¯E是所有策略的平均收益。从这个公式可以得出,当策略i的收益优于平均收益时,其比例就会增加。当这一比例单调增长时,采取策略i的群体数就能超过其他群体而占据优势。 根据例5 中的跨群体博弈, 定义群体一的策略为RI7在不影响理解的前提下,后文中我们也用RI 的符号来表达策略RI 的比例。:群体内博弈时选择P4,群体外博弈时选择P3; 定义群体二的策略为RII:群体内博弈时选择P3,群体外博弈时选择P4。 根据公式(**)及表1,可以计算RI、RII的复制动态变化。假设t时,两个群体的比例为qI和qII,也就是博弈者I 遇到博弈者I 和博弈者II 的概率分别为qI和qII。假设博弈者II 遇到博弈者I 和博弈者II 的概率也分别为qI和qII。8严格来说,这一比例不完全相同,而当我们考虑的群体数量较大时,这一差异可以忽略。我们可以得到: 因此, 当CI=CII,显然ERI=ERII。所以RI(t+1)=RI(t),RII(t+1)=RII(t)。也就是说,当群体的信号成本相同时,该动态的稳定点完全由起始的群体比例决定。这个结论的前提条件具有一定的特殊性。因为跨群体博弈的纳什均衡策略正好是博弈者各自的群体内最优策略。但是,从我们构建这一跨群体博弈的过程来看,这一特性总会出现。从这一意义上来说,这一结论也具有一般性。 以上分析可得出,群体的起始比例在群体的语言选择中起着重要的作用。 当CI CII,从公式(***)可以看出,ERI和ERII的大小关系可以很容易地由CI和CII的数值得出。但为了得出动态变化的速度,我们通过代入CI和CII的具体数值和计算机模拟来考察其动态变化。 首先假设CI=0.2,CII=0.1,即CI >CII。将数值带入表1,得到表2。 表2: CI=0.2 和CII=0.1 假设当t=0 时,两个群体比例为,起始策略比例也为。计算策略RI和RII的动态如下: 因此, 通过简单计算可以得出,t=1,qI=0.32 和qII=0.68。策略二的比例增长很快。通过简单的计算机模拟。可以得到,经过8 代复制,群体二的策略比例可以达到99%。也就是说群体二的收益要明显高于群体一。因而如果群体一可以通过学习转为群体二时,群体二的人数会迅速增长。而群体二的语言偏好是复杂度较低的语言。因此相对简单的语言会成为一个群体的最终选择。这一结论并不令人惊讶,因为这一结论的前提是群体二的信号成本是更低的并且群体二占有额外的交流信息。 更有意思的情形是当群体一的信号成本低于群体二的信号成本,也就是CI 表3: CI=0.1 和CII=0.12 通过简单计算得到: 因此, 很明显,群体一表现得比群体二出色。通过计算机模拟,我们得到在经过35代复制动态后,群体一策略比例可以达到99%。也就是说,群体一即使没有相应的背景知识,他们仍然可以通过调整信号使用成本来获得优势。换一个角度来说,最终群体一宁可不利用其背景知识的优势,只要语言使用成本够低,他们更愿意选择使用复杂度高的语言表达。 因此,学习和使用语言的成本在很大程度上会影响会话者对语言复杂性的偏好。当交流者在背景知识方面不占优势时,他们需要通过调整语言的使用成本和使用相对复杂的语言来获得优势。 近十年来,语言交流博弈与语用学的贝叶斯模型越来越受到重视。在对诸多语言性质的探讨中,佐尔曼(K.J.S.Zollman)的群体交流的区域语义形成模型([21])、桑塔纳(C.Santana)讨论歧义(ambiguity)优势的博弈模型([16])、托马斯(B.Thomas)建构的加强型语境学习的贝叶斯模型([19])与本文中的博弈模型在讨论的问题与形式化建构上较为相似,但也有诸多不同。我们逐一将我们的模型与这三个模型进行比较和讨论。 佐尔曼的博弈模型中,通过构建局部社会网络来讨论区域语义的形成。在刘易斯的经典信号博弈的基础上,佐尔曼加入了社会网络的群体博弈结构。从而使得单个博弈者的收益,由其周围的博弈者的行为决定。该模型解释了同一信号在不同的群体内形成不同语义的可能性。我们的复杂结构模型与这个模型的相似点在于,我们都考察了群体语言交流的行为。同时,也都保留了同一信号具有不同含义的可能性。但佐尔曼的信号博弈没有考虑群体之间背景知识的差异。而在我们的模型中,我们用博弈者的背景知识来区分不同群体的特征,且不同群体对于不同的语义是有不同偏好的。我们在前文的讨论中也论证了这一点。 桑塔纳的博弈模型在传统博弈模型的基础上做了两个扩展,第一个扩展为,信号博弈中的信号带有歧义性;第二个扩展为博弈者具有语境相关背景知识。基于这两个扩展,通过进化信号博弈的讨论,阐明了歧义性在进化信号博弈下的稳定优势。桑塔纳的博弈模型是与我们的复杂信号结构博弈最为接近的一个模型。但两个模型的侧重点不同。桑塔纳的模型侧重于讨论歧义性的产生。而我们的模型着重于讨论具有不同知识背景的两个群体在群体内以及跨群体的交流中对语言复杂度的偏好。正是由于这样的侧重点差异,导致两个模型在结构上的不同。桑塔纳的模型就没有对不同博弈者不同背景知识的刻画。 托马斯的模型着重探讨了博弈者如何在加强性学习的贝叶斯模型,逐渐学习和积累关于语言交流的背景知识(文中用语境来表述)。该模型与本文模型的相似点在于,我们都强调了不同博弈者具有不同背景知识的可能性。托马斯的模型更着重刻画当博弈者对彼此的背景知识未知的情况下,如何通过交流,学习彼此的背景知识,从而形成交流语境的过程。而本文的模型已经预设了博弈者对彼此的背景知识是已知的,我们着重讨论具有不同知识背景的群体对某一语言性质的偏好。 本文通过构建复杂信号结构博弈,试图探究社会因素是如何影响语言结构的,特别是语言复杂性结构。我们从刘易斯的信号博弈模型出发,进行了两个模型上的扩展。第一个扩展是加入带有复杂度的信号结构集,第二个扩展是使会话者拥有关于交流的背景知识。通过这个新的博弈模型,我们得到的主要结论如下: 1.当具有相同认知状态的群体进行博弈时,没有背景知识的群体偏好相对复杂的信号结构,而具有相关背景知识的群体在一定情况下更愿意使用相对简单的表达。 2.当具有不同认知状态的群体进行博弈时,语言使用成本和背景知识同时对语言复杂度的偏好产生作用。没有背景知识的群体可以通过降低语言使用成本和使用相对复杂的语言来获得优势。而具有背景知识的群体即使语言使用成本相对较高,也能在使用简单语言的情况下获得优势。 作为通过信号博弈对群体语言交流的社会因素的初探,本文也有诸多局限性。一是本文的许多结论是通过特定的例子给出的,这意味着结论的成立依赖于较强的模型假设。局限二是社会因素的考察过于单一,主要是通过不同群体知识背景来刻画。今后的工作中,希望可以在复制动态博弈的基础上,利用社会网络理论,加上具体的社会结构,从而更深入地考察社会结构对语言性质的影响。同时,通过弱化已有模型的相关假设,得到更一般的结论。5 跨群体交流的语言复杂性偏好


5.1 情况一:CI=CII

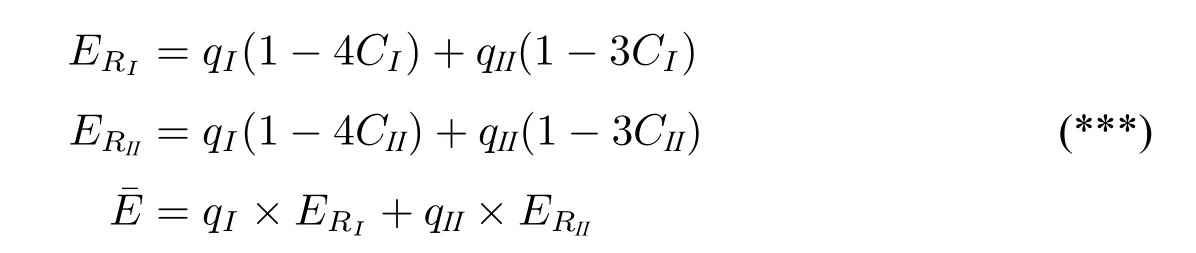

5.2 情况二:CICII


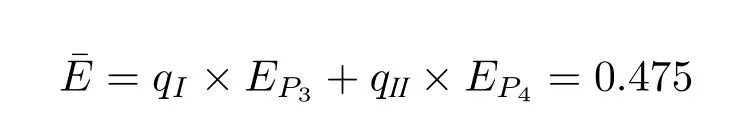

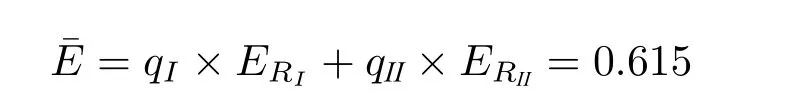
6 比较与讨论
