决策情境中的偏好提升
2020-06-28付小轩
付小轩
1 引言
一个理性主体通常需要具备在不同情境中做出决策的能力,而这些决策最终如何服从于他的理性,亦即,该主体的内在推理机制如何在决策过程中起作用?这个问题不仅仅是决策论(decision theory)所关注的对象,也是逻辑学中的偏好提升(preference lifting)理论所探讨的话题。
举一个简单的例子:张三需要决定是否购买100 元的房屋险。如果他选择购买的话,那么他将在房屋着火后获得100,000 元的保险赔偿;反之,他将省下100元保险费。这个决策情境可以用如下表格表示:
在决策论中,该表格的第一列统称为“张三的行为”,“a,b,c,d”称作“张三的行为可能导致的结果”。决策论的目的是通过对这四个可能结果的偏好对比,推导出张三应该选择哪个行为。而在偏好提升中,“a,b,c,d”可以看作是四个“状态”,“购买保险”看作是“a,b两个状态的集合”,“不购买保险”看作是“c,d两个状态的集合”。偏好提升理论的目的是基于不同状态之间的对比,推导出它们所构造出的不同集合间的对比。譬如,通过比较a、b、c和d,推导出张三更偏好集合{a,b}亦或者是集合{c,d}。由此可见,决策论和偏好提升理论在推理结构以及研究目的方面都一致,因此探讨二者的联系是一项自然且重要的研究。
然而,由于决策论和偏好提升理论在研究方法上的不同,将二者联系起来的工作目前主要面临两个挑战:
第一,决策论是定量化研究,而偏好提升理论是定性分析。譬如,假定张三的偏好序是c ≤a ≤b ≤d。1此处的偏好序表示的是:张三最偏好的结果是d,其次是b,再次是a,最后是c。那么偏好提升理论是基于这个序关系直接推导出张三应该选择{a,b}亦或者是{c,d},而决策论会给a、b、c、d赋上具体的数值(比如,a=1,b=4,c=−100,d=10),从而借助数值上的大小关系来表达出a、b、c、d之间的偏好关系,进而推导出张三应该选择哪个行为。除此之外,当决策情境伴随着不确定性时,这些可能结果的计算方式将不仅仅是单纯的赋值,同时还会引入概率的计算。由此就进一步加大了与偏好提升理论研究的差距。所以,本文首先需要探讨这类定量化研究与定性分析方式可以在何种程度上解决同样的问题,而它们之间的差异又体现在何处。
第二,迄今为止的偏好提升理论着重于研究带有确定性的决策情境,而较少将概率纳入考量,这就使得偏好提升理论在解释力方面相对较弱,并且较难运用到日常的决策情境当中。因此,本文也需要考量如何在偏好提升理论中加入概率,进而与决策论中结合概率的方法进行对比。
本文将主要围绕这两个挑战展开。第二节将介绍决策论的定量方法(效用函数以及期许度函数)、偏好提升理论中的四种主要提升方法以及结合概率的一些逻辑研究,从而探讨决策论的定量方法与偏好提升理论的联系和区别;第三节将给出一类偏好概率的逻辑模型,将它作为解决第二个挑战的初步尝试,并通过探讨它的性质来说明概率化的定性分析的优势与弊端;在最后的第四节,本文将总结主要的研究成果,并对未来的工作给予进一步的阐述与展望。
2 决策论的定量方法与偏好提升的定性分析
2.1 决策论中的效用函数以及期许度函数
决策论中的两个核心概念分别是:主体的偏好(preference)以及主体可实施的选择(options)。而主体做决策的过程就可以看作是他基于自身偏好对可能的选项做选择的过程。简单来说,面对两个可能的选项x和y,如果主体更偏好x,那么他会选择实施x,而数学上一般用y ≤x来表示这种情形;反之亦然。在更一般的数学设定中,对于一集可能的选项{x1,...,xn},主体基于对任意两个选项之间的偏好比较2此处,假定任意两个选项都可比较。,可以生成关于这个集合的偏好序列,譬如x1≤...≤xn。而这类偏好的序关系在决策论中通常用如下的效用函数(utility function)U:X →R 表示:
任取一个选项集X,对任意的x,y ∈X,U(x)≤U(y)⇔x ≤y。
从而通过以上定量化(数值间)的比较,主体会选择具有最大效用值的x(此处,不妨假定X={x1,...,xn},那么U(x)=max{U(x1),...,U(xn)})。
然而,在实际的决策情境中,主体的选择往往伴随着不确定性,因此决策论在上述定义的基础上加入了概率,由此引入了期望效用(expected utility)。此时,主体的偏好序关系通过期望效用值之间的大小比较体现出来,并且他会选择期望效用值最大的选项,而不再是效用值最大的选项。对于期望效用值在实际决策情境中的定义,主要有以下两种方式:
第一是萨维奇(L.J.Savage)([12])提出的计算方式:
这个等式表达的是:对于每个状态si而言,主体事先都分配了一对数值,它们分别是si出现的概率以及在si上实施行为f会产生的效用值,通过计算这一对数值的乘积,可以得出si上的期望效用值;接下来,主体再对每个si的期望效用值进行求和,以此来计算出行为f作用在整个S上的期望效用值。
萨维奇的理论为偏好关系提供了概率化的解释,该解释可以用如下等价关系表示:
对任意行为f和g而言,U(f)≤U(g)⇔f ≤g。3这个结论保证了即使加入了概率,偏好序依然可以用效用之间的数值比较来表示。
在探讨这个等价关系的过程中,他提出了著名的“确定性原则”(Sure Thing Principle)([12],第21–22 页)。该原则可以表述如下:
将状态集合S划分成两个互斥的子集S′以及S −S′,如果f、g和f′、g′同时满足:(i)f、g在S′导致相同的结果,并且f′、g′在S′也导致相同的结果;(ii)f、f′在S −S′导致相同的结果,并且g、g′在S −S′也导致相同的结果;(iii)f ≤g;那么就有f′ ≤g′。
这个原则要求了行为与状态之间的概率相互独立,亦即,在任意可比较的状态中,如果主体总是更偏好其中的一种行为,那么无论一个状态发生的概率是多少,他对这两种行为的偏好排序都会保持不变。这预设了主体必须优先了解哪种划分状态的方式可以保证这种独立性。但是这种对于概率分布的先天预设限制了萨维奇对于概率的设定。
第二是杰弗里(R.C.Jeffrey)([10])提出的计算方式:

在该公式中,p表示一个命题,P(pi |p)表示的是:在p发生的情况下pi发生的条件概率,D:P→R 是一个定义域为命题集的期许度函数(desirability function)。它与萨维奇的效用函数的差异在于:这个函数定义域中的任意一个元素既可以是一个状态也可以是一个行为(或行为的结果)。
在偏好关系的概率化解释方面,杰弗里的定义也能保证:
对于任意的命题p和q而言,D(p)≤D(q)⇔p ≤q。
它表明了任意一个偏好关系都可以用期许度函数来表示。与此同时,杰弗里在[10]中弱化了确定性原则的条件,提出了一个所谓的平均值(averaging)原则。该原则可以用如下形式表述:
任取一个命题集合Ω(其中,⊥/∈Ω),如果p,q是Ω 中彼此互不相容的两个命题,那么p ≤q ⇔p ≤p ∪q ≤q。
这个条件表示:对于两个不相容的命题p和q而言,p ∪q蕴含了——只能是p和q的其中之一为真。由此,假定q比p更令人期许(desirable),那么p ∪q既不能比p更不令人期许,也不能比q更令人期许。这是因为p ∪q:要么p更令人期许要么q更令人期许。不过,杰弗里的定义也遗留了一个问题:即使主体的偏好满足他所设定的条件,那么既不能保证只有一个概率函数代表他的信念,也不能保证代表他意愿的期许度函数的唯一性。进而,这种定义唯一性的缺失也成为杰弗里计算方式的一个重要弊端。
综上可见,萨维奇与杰弗里的计算方式都有各自的不足,但是本文的重点并不是回应、修正他们各自理论的不足,而是通过探讨效用函数与期许度函数,以此来说明他们二者讨论偏好(或者说是决策)的方式本质上一样。这是因为可以将期许度函数D看作是从行为集合到实数的函数,“一个p命题”看作是“行为f”,对任意的“i”而言,“i”可以看作是“指标集”,它表示了“不同的状态”,而“pi”就表示了“在i状态中p行为所导致的后果”,“P(pi |p)”表示了“实施p行为的i状态出现的概率”。由此可见,二者都是通过考虑每个行为所产生的后果值(效益值或者期许度)以及发生该行为的状态所出现的概率,来计算这个行为的最终总收益(期望值或者期许度)。
2.2 偏好提升的四类基本方式及其逻辑研究
关于主体如何将他的偏好序从状态间的比较(或可能结果间的对比)提升到状态集合间的比较(或行为间的对比),刘奋荣([11])以及范丙申(J.van Benthem)([2])都探讨了具体的方法。利用逻辑量词,这些提升方法主要分为以下四类:
• ∀∃-法:如果∀x ∈X ∃y ∈Y:x ≤y,那么X ≤Y;
• ∀∀-法:如果∀x ∈X ∀y ∈Y:x ≤y,那么X ≤Y;
• ∃∀-法:如果∃x ∈X ∀y ∈Y:x ≤y,那么X ≤Y;
• ∃∃-法:如果∃x ∈X ∃y ∈Y:x ≤y,那么X ≤Y。
其中,∀∃-法以及∀∀-法被较为广泛地在实践中使用。哈尔彭(J.Y.Halpern)为偏好提升理论中的∀∃-法提供了公理化。([7])范丙申、吉拉德(P.Girard)与罗伊(O.Roy)认为用∀∀-法所定义的偏好提升正是冯莱特(G.H.von Wright)在[13]中研究偏好时的想法。([3])哈勒戴(W.H.Holliday)和埃克尔德(T.F.Icard)为了避免亚尔钦(S.Yalsin,[14])所提出的蕴涵问题,提出了偏好提升的新方法。([9])他们在∀∃-法的基础上加上了一个要求——X ≤Y当且仅当存在一个从X到Y的通胀(inflationary)函数,并且该函数是单射。其中,一个函数f:X →Y是通胀的指的是:对∀x ∈X,x ≤f(x)。而这也等价于∀∃-法的定义。在该文章中,他们认为主体根本不会有足够的信息来完全确定命题(或者说状态)的总体排序,因此允许了许多不可比性。哈里森-特瑞那(M.Harrison-Trainor)等人表明这个新规则相对于不精确概率的比较逻辑([1])是可靠并且完全的。([8])其中最为重要的是:通过这些设定,他们以概率的方式解释了新∀∃-法,并用定性的定义方式捕捉了其背后的定量推理。
第一个将概率解释引入“≤-关系”的逻辑研究可以追溯到[6]。德菲尼蒂(B.de Finetti)推测:对于任意有穷的非空集S而言,考虑其所有子集X和Y上的“≤-关系”,那么一定存在一个概率P使得:
X ≤Y当且仅当P(X)≤P(Y)
并且满足以下条件:
1.∅≤X;
2.并非S ≤∅;
3.X ≤Y或者Y ≤X;
4.如果X ≤Y并且Y ≤Z,那么X ≤Z;
5.X ≤Y当且仅当X ∪Z ≤Y ∪Z,其中Z与X、Y的交集都为空。德菲尼蒂的提议不仅保证了≤的一般属性4此处的属性指的是:自反、反对称以及传递。,而且还为“≤-关系”的解释提供了一系列必要条件,以此为偏好提升找到了概率化的表示方法。
范·埃克(J.van Eijck)和雷尼(B.Renne)重新开始了关于德菲尼蒂的研究,并且提出了认知“邻域模型”中的认知概率更新逻辑,探讨了“信念”算子(该算子可以看作置信度(plausibility)间的“≤-关系”)的概率化,并将“更相信某个世界”解释为“这个世界出现的概率大于”。([4])在[5]中,他们进一步利用“权重(weight)函数”为这种解释方式提供了逻辑模型,将“更相信某个命题ϕ”解释为“ϕ出现的权重比¬ϕ出现的权重更高”。从而,他们通过对比状态之间的权重(或者说是概率),将置信度关系的比较提升到状态集合之间。
2.3 联系与区别
从2.1 关于决策论的概述和讨论可以看出,效用函数(期望效用)和期许度函数实际上是相同结构的计算方式。本节将主要从杰弗里的定义方式出发,只利用唯一的函数(期许度函数)来探讨决策论和偏好提升理论之间的关系。
借助杰弗里的定义,主体会选择期许度更高的命题(或者说是行为),亦即,对两个命题X和Y来说,如果D(X)≤D(Y),那么X ≤Y。一般而言,X和Y可以看作两个集合,它们各自包含了满足这两个命题的所有状态,或者说是实施这两个行为会导致的两个可能结果集。由此,D(X)和D(Y)都可以看作是借助“D(x)≤D(y)⇔x ≤y”5该等价关系只能用在可能的结果上,或者更形式地说是用在形如pi 以及qj 的公式上。这个等价置换后,利用“偏好值”、概率进行求和所计算出来的结果。而偏好提升理论和该定义的联系与差别主要在于:
第一,偏好提升理论没有“D(x)≤D(y)⇔x ≤y”的等价置换过程,而是直接考虑“x ≤y”这个关系从个体收敛到集合的结果。这个“收敛”过程在决策论当中是通过求和的形式表示。但是由于偏好提升理论无法对个体间的关系进行“求和”,这需要它能够通过其他的规则(譬如,偏好提升理论的四种基本方式)来表现出此类“求和”的方式。实质上,这四种提升方式无法表示出决策论中的“求和”结果。这不仅因为它们无法计算概率,也因为这种计算方式并不要求对于≤偏好关系进行求和(甚至也无法进行求和)。
第二,决策论在求和过程中既涉及到了每个命题(结果或者说是状态)的期许度(或者说是效益),也涉及到了这些命题出现的概率,而在迄今为止的偏好提升理论中,这两个部分基本都是分开考量。换句话说,偏好提升理论要么直接考虑每个命题之间的“≤”偏好关系,要么通过概率的方式来体现这个“≤”关系——更偏好(或者说是更相信一个状态)当且仅当这个状态出现的概率更高。譬如,[4]就利用了这种概率化的定义方式。这也就表明,当探讨命题集合(或者说是行为)之间的偏好关系时,偏好提升理论并没有综合考虑命题之间的偏好关系以及这些命题各自出现的概率。
为了贴近决策论的这种综合考量,本文将在偏好提升理论的基础上,引入一种“两两比较提升法”。
3 偏好概率模型——两两比较提升
综合第二节的讨论可以看出,偏好提升理论与决策论匹配间的缺口在于:如何通过定性的方式将“≤-关系”与概率相结合。本节将以两个行为6此处的“行为”指的是这两个行为所各自导致的所有可能结果构成的两个集合。之间的对比为出发点,通过定义一种“两两比较提升法”,将两类可能结果之间的对比提升到行为之间的比较,从而令主体能够在这两个行为之间做出决策。直观上,本节接下来将提供一种较决策论的量化方式而言“更粗糙”7此处的“粗糙”指的是:通过“求和”的计算方式,任意两个行为都可以通过比较数值大小来确定偏好,但是可能存在一些行为在偏好提升理论当中不可比较,但是在决策论中可以比较。回顾引言当中的例子,主体无法直接得出更偏好哪个行为,却可以通过给它们不同的效用值以及概率赋值计算出选择哪个行为。而较原有的偏好提升理论而言“更细致”8此处的“细致”指的是:可以适用于带有不确定性的偏好提升(决策情境),将可能结果之间的比较以及它们出现的概率综合起来考量。的计算方式。
3.1 两两比较提升法
定义1(两两比较提升法).给定任意两个行为所产生的结果集X和Y,Y比X更被偏好,亦即,X ≤Y当且仅当如下条件被满足:
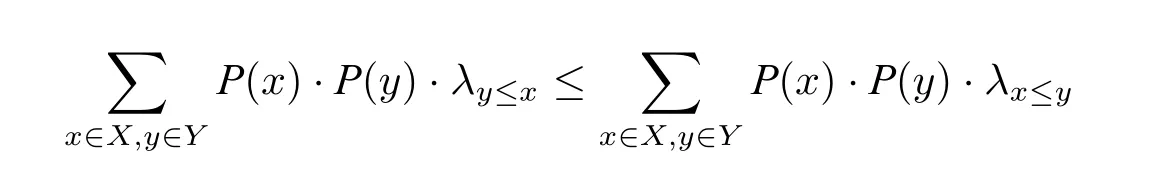
其中,
•P(x)是x出现在X中的概率,而P(y)可以被类似地定义。

直观上,任取X×Y中的有序对⟨x,y⟩,如果“y ≤x”这类关系出现的概率比“x ≤y”这类关系出现的概率小,那么主体就会更加偏好Y。此处比较的是X和Y两个集合中形如“x ≤y”和“y ≤x”这两类关系各自出现的总概率。
例如,集合X={x1,x2}以及Y={y1,y2},它们元素之间的偏好关系是:x1≤y1,x1≤y2,x2≤y1,且y2≤x2。不妨假定满足以上关系的四个有序对出现的概率相同,那么借助定义1,主体会更加偏好Y。此处当然也可以假定每个有序对出现的概率不一样,它们具体的概率都取决于主体对于每个状态(或者说是结果)的置信度。
相较于偏好提升理论而言,两两比较提升法不再是定性化的关系提升,而是定量化的概率提升,并且它可以直接运用在带有不确定性的决策情境中。无论是原有的四类基本方式,抑或是偏好提升理论的近期研究,都仅仅关注个体关系上升到总体后的变换,不关注每个个体关系出现的概率。在实际的决策情境中,这可能会导致小概率事件决定了最终偏好。举个简单的例子,在比较两个集合X和Y时,X中有主体最偏好的元素,但是该元素出现的概率逼近于零,而Y中的任意元素至少和X中的其他元素一样被偏好。在这种情境下,利用基本方式中的∀∃-法,主体会选择X;而两两提升比较法却可以同时将概率纳入考量,如果两个集合的基数足够大,那么主体可能会选择Y。在结合概率方面,虽然置信度关系对“≤-关系”进行了概率化解释,但是两两提升比较在它的基础上增加了一个维度——“X ≤Y”并不是仅仅因为Y出现的概率更高,而是Y中主体更偏好的元素出现的概率更高。
相较于决策论而言,两两比较提升法将求和过程分解成以下步骤:
1.考虑两个集合中所有元素的可能配对组合;
2.考虑每个有序对之间的大小关系,并乘以该有序对出现的概率;
3.分别计算出“x ≤y”这类关系出现的概率总和以及“y ≤x”这类关系出现的概率总和,再进一步进行比较。
这三个步骤中的重点在于第三个步骤的设定:此处抛弃了决策论中的等价置换——“D(x)≤D(y)⇔x ≤y”,而直接利用元素之间的的可比较关系,将它们用λ函数计算出来:对于任意的两个元素x和y而言,如果有x ≤y,那么λx≤y就需要“记录”这个关系(用1 表示),从而通过乘以这对有序对出现的概率,以此作为“求和”过程中的一部分;反之,λy≤x不需要“记录”该关系。因而在最终对比“x ≤y”和“y ≤x”这两类关系的概率总和时,λ函数相当于杰弗里的期许度函数D,只不过λ运算不需要精确到x和y的具体数值。
不过,这种两两对比的方式还是无法模拟决策论中的所有计算。其中比较显著的的一个差异在于:决策论对于偏好有两个基本设定,那就是偏好之间的“≤-关系”是可比较并且传递的。但是这种两两对比的方式却会导致以下问题:
命题1.定义1 中的“≤-关系”可比较但是并不传递。
证明.≤关系的可比较性可以由定义直接得证。以下将通过提供三类反例来说明该关系的非传递性。
•“=-关系”非传递性:假设X={2},Y={3}且Z={1,4},这些元素之间的偏好关系是1<2<3<4,并且对任意两个集合A和B而言(A和B用来指代X、Y、Z当中的任意二者),每个有序对出现的概率都是。那么根据定义1 可以得出:X=Z,Y=Z并且X •“<-关系”非传递性的第一类例子:假设X={2,6},Y={1,4,5}且Z={3},这些元素之间的偏好关系是1<2<3<4<5<6,并且对任意两个集合A和B而言,每个有序对出现的概率都是。那么根据定义1 可以得出:Y < X,Z < Y并且X=Z。然而这就与“<”的传递性相矛盾。 •“<-关系”非传递性的第二类例子:假设X={2,3,7},Y={1,5,6}且Z={4},这些元素之间的偏好关系是1<2<3<4<5<6<7,并且对任意两个集合A和B而言,每个有序对出现的概率都是。那么根据定义1 可以得出:Y 前两个反例揭示了“≤-关系”的非传递性。第三个反例还表明这种定义方式允许存在“<-循环”。因此,两两比较提升法所定义的“≤-关系”并不传递。 在以上反例中,有序对的概率平均分布是构造反例的关键。虽然由此证明了“两两比较提升法”并不保证偏好关系的传递性,但是这种不传递性在实际运用中并不少见。 接下来简单介绍这个方法的一个应用: 例1(“概率悖论”:掷骰子).张三邀请李四玩骰子。现在桌子上有三个骰子:A,B以及C,它们分别是: • A={3,3,5,5,7,7} • B={2,2,4,4,9,9} • C={1,1,6,6,8,8} 张三要求李四首先选择一个骰子,然后他选择剩下两个当中的一个。在投掷两个骰子的过程中,投掷更大数字的人就是胜利者。那么张三该如何做决策? 在以上决策情境中,无论李四选择了哪个骰子,张三都可以有获胜的策略。这是因为:通过对任意两个骰子之间的点数以及出现概率的比较,可以推断出: A 如果李四选择A,那么张三将选择C;如果李四选择B,那么张三将选择A;如果李四选择C,那么张三将选择A。显然,这三组之间的偏好并不具有传递性,而定义1 恰好可以用来解释这种“概率悖论”。 基于上述对于两两比较提升方法的阐释,本文接下来引入“两两比较偏好概率模型”。在设定它的语言和模型时,本文只考虑单一主体的情况,所以省略了偏好关系符号中表示主体的下标。 定义2(语言:Lpref).给定一个非空的命题变号集合Prop,Lpref的语言定义如下: 其中,p ∈Prop,并且ϕ、ψ是命题变号或者仅仅是由布尔运算构成的命题。 在语义上,ϕ ≤ψ表示了公式ψ至少和公式ϕ一样被偏好。 定义3.偏好概率模型是一个四元组M=⟨S,⪯,V,P⟩,其中: •S是一个非空且可数的状态集; •V指派给每个p ∈Prop 一个S的子集; •P是从S到[0,1]的一个概率函数。 注意:根据以上P的定义,本文将使用条件概率来表示“给定Z后,P(z)的值”。 定义4.给定Lpref语言中的一个偏好概率模型,它的可满足关系(⊨)定义如下: 按照以上定义,本文接下来讨论该逻辑的一些性质: 命题2.以下列举出该逻辑的一些有效式和非有效式: 有效式: • |=⊥≤ϕ,由定义4 可直接证明。 说明:偏好概率模型保证了任意公式的概率都大于等于0。 • |=ϕ ≤ϕ,由定义4 可直接证明。 说明:偏好概率模型保证了偏好关系的自反性。 • |=ϕ ≤ψ ∨ψ ≤ϕ,由定义1 以及定义4 可证。 说明:偏好概率模型保证了偏好关系的完全性。 • |=ϕ<ψ →¬(ψ <ϕ),由定义4 可直接证明。其中,ϕ<ψ:=(ϕ ≤ψ)∧¬(ϕ=ψ),而ϕ=ψ .=(ϕ ≤ψ)∧(ψ ≤ϕ)。 • |=(ϕ ≤ψ)→(ϕ ∨χ ≤ψ ∨χ),其中∥ϕ∥∩∥χ∥=∅且∥ψ∥∩∥χ∥=∅。由定义4 以及⪯-关系的传递性可证。 说明:偏好概率模型保证了偏好关系概率化后的有穷求和属性。 • |=(ϕ ≤ψ)↔(ϕ ≤(ϕ ∨ψ)≤ψ)。 证明.易见,该等值式从右往左成立。从左往右的证明如下: 假设|=(ϕ ≤ψ)。那么由定义4 可知: 现在考虑两种极端情况: 1.“∥ϕ∥⊆∥ψ∥,抑或是∥ψ∥⊆∥ϕ∥”的情况。在这两类情况中,∥ϕ ∨ψ∥=∥ψ∥或者是∥ϕ ∨ψ∥=∥ϕ∥。由假设、|=ϕ ≤ϕ以及|=ψ ≤ψ可以得出|=ϕ ≤(ϕ ∨ψ)≤ψ。 2.“∥ϕ∥与∥ψ∥交集为空”的情况。首先证明|=ϕ ≤(ϕ ∨ψ)。由于 同理可证|=(ϕ ∨ψ)≤ψ。 综上可见,等值式从左往右得证。 说明:偏好概率模型满足2.1 节中杰弗里所提出的平均值原则。该条件也可以看作是萨维奇所提出的“确定性原则”的弱化,它不需要区分行为与状态,也不需要预设二者之间的概率相互独立。这也进一步说明偏好概率模型保证了——期望效用以及期许度函数的重要性质。 • |=(ϕ ≤¬ϕ)→(ϕ ≤⊤),由有效式6 以及定义4 可证。 说明:结合下述第一个非有效式可以看出,偏好概率模型并不要求任意公式出现的概率都要小于等于重言式出现的概率。而有效式7 就给出了一种充分条件——它能够保证一类公式出现的概率总是小于等于重言式出现的概率。 • |=(ϕ ≤ψ)∧(χ ≤ψ)→(ϕ ∨χ ≤ψ)。 证明.假设|=(ϕ ≤ψ)∧(χ ≤ψ)成立。那么由定义4 可知: 在∥ϕ∥⊆∥ψ∥,或是∥ψ∥⊆∥ϕ∥,抑或是∥ϕ∥与∥ψ∥交集为空的三种情况下,由(i)和(ii)易见|=ϕ ∨χ ≤ψ成立。现在考虑∥ϕ∥∩∥ψ∥=X,其中X非空的情况: 进而,结合(i)、(ii)、(iii) 以及(iv) 可以得出。因此,|=ϕ ∨χ ≤ψ成立。 说明:偏好概率模型满足了一个新特点:对于三个对象(或者说是公式)而言,假如主体有个最偏好的对象,那么即使将另外两个对象结合在一起,主体依然会选择他最偏好的那个对象。 非有效式: •⊭ϕ ≤⊤ 证明.假设模型M 由以下部分组成:S={1,2},⪯={⟨1,1⟩,⟨1,2⟩,⟨2,2⟩},V(p)={2},并且。那么 进而,由定义4 可以得出M,2|=⊤≤p。 •⊭(ϕ ≤ψ)∧(ψ ≤χ)→(ϕ ≤χ),由命题1 可证。 说明:偏好概率模型中的偏好关系并不传递。 •⊭(¬ϕ ≤ϕ)→(ψ ≤ϕ)。 证明.假设模型M 由以下部分组成:S={1,2},⪯={⟨1,1⟩,⟨1,2⟩,⟨2,2⟩},V(p)={2},V(q)={1}并且。那么,由定义4 易见:M,2|=¬p ≤p,然而M,2 ⊭q ≤p。 •⊭¬ϕ<ϕ →(¬(ϕ ∧ψ)<(ϕ ∧ψ))。 证明.假设模型M 由以下部分组成:S={1,2},⪯={⟨1,1⟩,⟨1,2⟩,⟨2,2⟩},V(p)={2},V(q)={1}并且。易见,∥p ∧q∥=∅,并且∥¬(p ∧q)∥={1,2}。因此,由定义4 可以得出:M,2|=¬p < p,然而M,2 ⊭¬(p ∧q)<(p ∧q)。 •⊭(⊥<(ϕ ∧¬ψ))→(ψ <(ϕ ∨ψ))。 证明.假设模型M 由以下部分组成:S={1,2},⪯={⟨1,1⟩,⟨1,2⟩,⟨2,2⟩},V(p)={1},V(q)={2}并且。易见,∥p ∧¬q∥={1},并且∥p ∨q∥={1,2}。因此,由定义4 可以得出:M,2|=⊥<(p ∧¬q),然而M,2|=q >(p ∨q),亦即M,2 ⊭q <(p ∨q)。 由此可见,偏好概率逻辑满足直观上偏好关系应该具有的大部分性质,并且也除去了那些显然不应该具有的性质。与此同时,这些有效式也满足德菲尼蒂在逻辑上关于“≤-关系”概率化的研究,尤其是其中的第六条吻合了决策论所关注的重要原则——确定性原则。虽然这种定义方式不能保证传递性,但是也不失为一种利用偏好提升理论逼近决策论计算方式的尝试。 本文针对引言所提出的两个挑战,在第二节中具体探讨了决策论与偏好提升理论之间的联系与差异,并通过在第三节中引入“两两比较提升法”,将概率纳入偏好提升理论进行考量,介绍了其中的λ函数与概率的结合,尝试利用定性的分析方式来逼近决策论的定量计算结果。尤为重要的是,第三节分析了这种新的定义方式相较于原有偏好提升方式的优势,以及它在何种程度上可以解决决策论的问题,这也包括了它相较于决策论的缺失——偏好关系没有传递性。除此之外,作为一种初步尝试,本文还为这种“两两比较提升法”提供了逻辑模型,并结合了决策论与偏好提升理论的研究,讨论了该模型的一些重要性质。 关于如何在偏好提升方法或者是逻辑模型中引入概率,逻辑定义方面可以做更多的尝试。譬如可以基于基本的∀∃-法,考虑以下引入概率的方法: • 如果∀x ∈X ∃Y′ ⊆Y:P(Y′ |Y)>0.5 &∀z ∈Y′(x ≤z),那么X ≤Y; • 如果∀Y′ ⊆Y:P(Y′ |Y)>0.5,那么∀x ∈X∃y ∈Y′(x ≤y)。 当然,针对偏好提升理论的概率化研究,可以引入更多的定义方法,并进一步逼近决策论的计算能力。对比于第三节所提出的“两两比较提升”,这些方法本质上都是希望借助对比两类关系——“≤-关系”和“≥-关系”各自出现的总概率大小,来实现定性化的概率求和,从而计算出主体的选择。以上两种新的定义方式可以保证偏好关系之间的传递性,其中的一个重要原因就在于它们都不需要从“两两集合之间的概率对比”过渡到“所有集合之间的概率对比”9这种“不同集合间都可以进行两两对比”与“整个集合间可以进行排序(排除了环状)”并不是等价的概念,从右往左是自然的结果,但是从左往右存在反例。譬如在第三节所举出的三类反例。,而是直接选择所有集合中的部分集合(譬如出现概率大于0.5 的那些集合)进行排序。 总之,本文主要希望通过抽象出决策论计算方式与偏好提升理论背后的数学结构,揭示出它们结构上的联系,并利用它们二者之间的差异,表明这种研究的必要性以及可能性。在未来的研究中,可以考虑更丰富的定义方式来进一步搭建起联结决策论与偏好提升理论的桥梁。以下列举一些可能的研究课题: •“两两比较提升法”与邻域语义学(neighborhood semantics)的结合。从上述关于“偏好概率模型”的讨论可以看出,⊥和⊤公式的有效性并不满足排中律。这就说明满足这两个公式的集合有可能存在重叠,而邻域语义学恰好具有这种性质。 • 引入其他的“测量”方式(譬如拓扑学的方式)来进行偏好提升理论的定量化研究,从而避免第三节中概率空间的二元划分所导致的非传递性。 • 结合动态概率逻辑,将决策论中的其中一个形如“效用值与概率的乘积”的公式作为初始的静态概率模型引入,并且将每一步“加法”都转变为“初始静态模型与行为模型的叉乘”,从而分解为逐步求和的计算。3.2 两两比较偏好概率模型

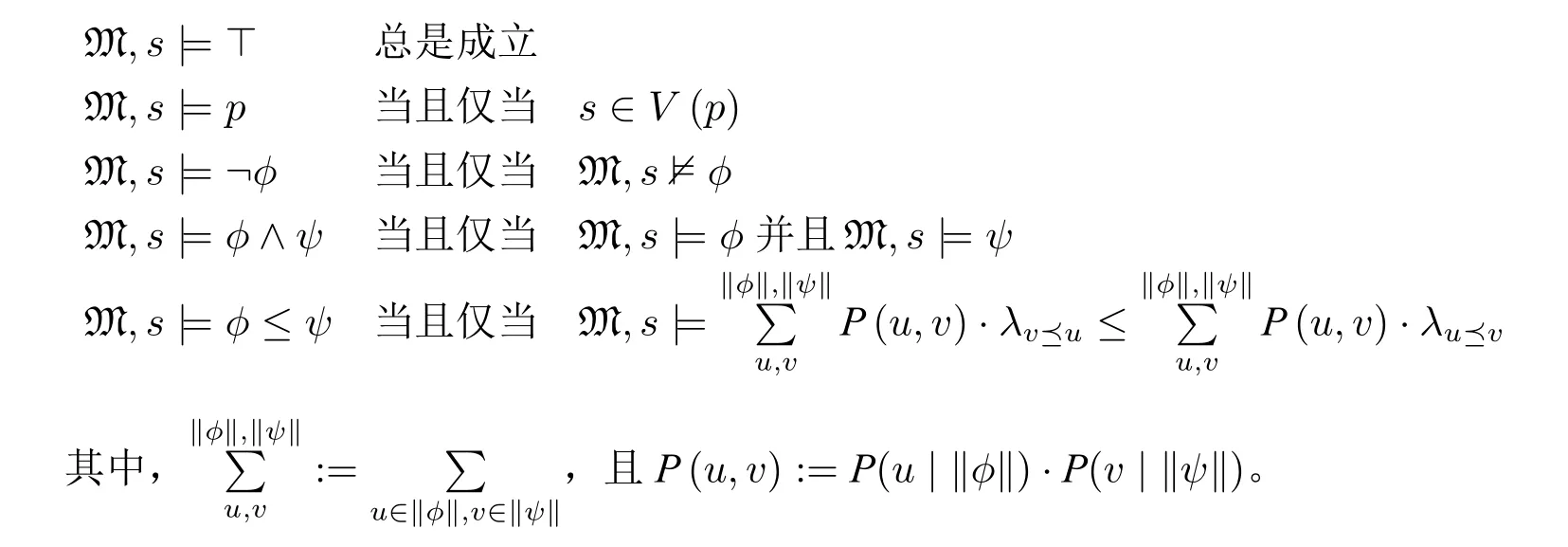


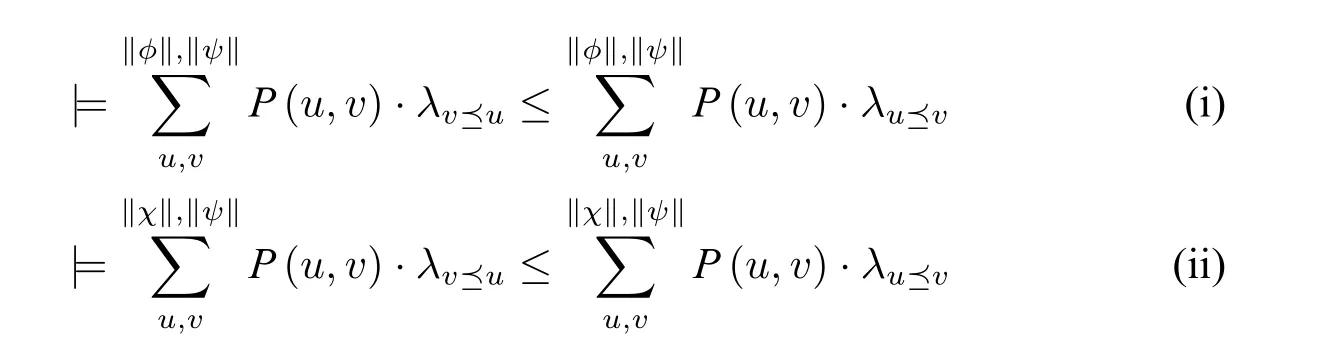
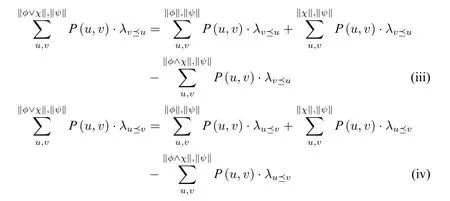
4 结语
