The Early Responses of Air-backed plate subjected to underwater explosion with aluminized explosives

Jian Liu, Feng-jiang An, Cheng Wu, Sha-sha Liao, Ming-xue Zhou, Dong-yu Xue

State Key Laboratory Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China

Keywords:Aluminized explosives Underwater explosion Air-backed plate Early responses

ABSTRACT This work aims to research the effects on the early responses of the air-backed plate subjected to the loading generated by the underwater explosion with aluminized explosives. The loading characteristics of underwater explosion for ideal explosive(TNT),aluminized explosives(RS211 and RBUL)are obtained experimentally. The tested aluminized explosives have different energy output compared with TNT.Based on the Taylor plate theory, the early responses of the air-backed steel plate affected by the measured loading is analyzed. The analytical results indicate that the pressure curve of the shock wave within 1 time decay constant is the main factor affecting the kick-off velocity of the plate when cavitation occurring. The velocity responses of the plate produced by the loading of RS211 and RBUL are obviously different with that of an equivalent TNT charge, which also indicates validity and suitability should be noticed in the case of substituting TNT for aluminized explosives. Moreover, the uncertainties in the responses of the plate produced by RS211 and RBUL are much larger than TNT.

1. Introduction

The survivability of ships and their equipments in the war environment is a major consideration in the design of ships[1].The Navy shock involves the protection of equipment from the effects of the underwater explosion[2,3].Plate panel is a common structural component of ships [4,5]. During the last two decades extensive research was conducted to assess the response and deformation failure of ship hull [6-13]. C.F. Hung et al. [6] compared experimental and numerical results concerning the elastic dynamic response of an air-backed rectangular aluminum plate subjected to an underwater explosion. Riley Mark J. [11] (2010) made an investigation about failure mode transition in air-backed plates from near contact underwater explosions. Hammond Lloyd et al.[12](2000)presented an effective method for predicting the static behavior of a simple mild steel strut undergoing gross deformation.Rajendarn R [13]. aimed to bring out a comparative procedure for the damage assessment between air-and water-backed plates so that the response of the latter can be presented in terms of that of the former.

In general,input to the ships on the underwater explosion is the loading, and output is the structural response by the ships.Aluminized explosive is an important type of charge for underwater weapons,which has different energy output compared to the TNT [14]. But in the theoretical analysis and numerical simulation of the responses of Taylor plate subjected to underwater explosion loading, TNT is usually used as a source of explosion loading or substituting TNT for aluminized explosives simply. Because the loading profile of TNT is very well characterized, other explosive loading could be obtained scaled by an appropriate equivalence factor. During the underwater explosion, mass and energy are considered mostly in the equivalent method [15]. However, the deviation of the results from the equivalent method is hardly evaluated [16]. There have been rarely research on the ship shell responses resulted from the characteristic of the loading of different explosives.

So this study mainly analyzes the effects on the early responses of the plate generated by the underwater explosion loading of the tested aluminized explosives. Firstly, the underwater explosion experiments of the TNT, RS211 and RBUL are conducted. Then the characteristics of the loading of the tested aluminized explosives(RS211 and RBUL) are obtained, which are different from that of TNT.And a new model different from the traditional description for the pressure of underwater explosion shave is proposed.Finally,the early responses of the air-backed plate are analyzed considering decay models of underwater shave, TNT equivalent methods and uncertainties of the explosion loading, based on the experimental data.

2. Underwater explosion experiment and results

The characteristics of the underwater explosion loading of aluminized explosives will make the ship structure be deformed and damaged seriously. In order to obtain the differences of the underwater explosion loading between the aluminized explosives and the ideal explosive, the underwater explosion experiments of the three types of explosives were conducted.

As is shown in Fig.1,the underwater explosion experiment was conducted in a pool, which diameter and depth were 85 m and 13.5 m, respectively. The stand-off distances were 3 m, 4 m, 5 m,6 m, and 7 m, respectively. The charge was installed at a depth of 7 m underwater,which could counteract the effects of two different properties of reflection from the solid wall and the free surface effectively.In Fig.1(a),there is a pressure sensor at each stand-off distance position and the measured signal was recorded by the data collection system. And the underwater explosion for each type of charge was performed twice.

The ideal explosive is TNT and aluminized explosives are RS211 and RBUL,respectively.In this study,the charge shape is spherical.The weight of three types of explosives is all 5 kg.The properties of three tested explosives are shown in Table 1.

The data collection system includes the debugger, oscilloscope,synchronous delay machine, detonator and underwater pressure sensor.The sensor used for this experiment is underwater pressure sensor of PCB.It is a sensor for measuring shock pressure generated by underwater explosion, and its model name is W138A10 PCB.W138A10 is an ICP-type sensor that produces output within ±5 V for measuring shock pressure and its maximum measurement pressure is 68950 kPa. The underwater explosion pressure measuring system is advanced and meets accuracy requirements.

The underwater shock wave pressure signals measured by five sensors were recorded by the oscilloscope. Fig. 2(a) and Fig. 2(b)represent the pressure time history curve of the TNT at different stand-off distances, which include underwater shock wave stages and bubble pulsation stages. It can be seen that the shock wave peak pressure gradually decreases with the stand-off distance (R)increasing. At the same time, the curve of shock wave gradually widens as the distance increases. The time decay constant (θ)gradually becomes larger,which is defined as the time taken by the shock wave pressure to decay to 1/e of the value of the peak pressure. The bubble period does not change with the distance compared with the shock wave.

The measured pressure signals of TNT and RBUL(R=4 m)can be seen in Fig.2(c)and(d).The value of the peak pressure of the RBUL is slightly higher than that of TNT at the same stand-off distance.There are also two significant differences between the TNT and RBUL. On the one hand, the bubble pulsation period of RBUL is much larger than that of TNT. On the other hand, the time decay constant of RBUL is significantly larger than TNT. So the experimental values determined directly from the measured signals of the shock wave peak pressure (Pm) and the time constant (θ) are summarized in Table 2 and Table 3.

According to the suggestions of G. Bjarnholt and Sany H G.[17,18], the shock wave energy, bubble energy and total energy averages over several distances of each type charge are calculated as shown in Table 4. For example, the shock wave energy, bubble energy and total energy of RBUL are 1.70,2.23,and 2.04 times TNT equivalent with the same charge weight, respectively. Taking into account the charge density, the shock energy, bubble energy and total energy of RBUL are 1.92, 2.52 and 2.31 times TNT equivalent with the same volume, respectively.

For the underwater shock wave pressure within 1θ, Cole [19]proposed a single exponential decay model:

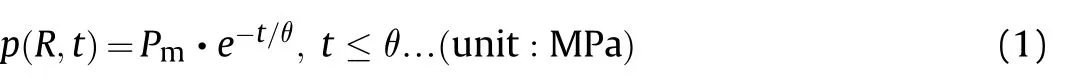
The peak value of the shock pressure(Pm)depends on the standoff distance and weight of the charge.The peak value of shock wave is expressed by the empirical Eq.(2)when the peak value of shock wave is less than 130 Mpa [20]:

Fig.1. The schematic diagram of the underwater explosion experiment. (a) The arrangement of the explosive charge and sensors; (b) The data collection system; (c) The tested spherical charge of RS211; (d) The splashing water column after detonation.

Table 1 Properties with respect to three tested explosives.

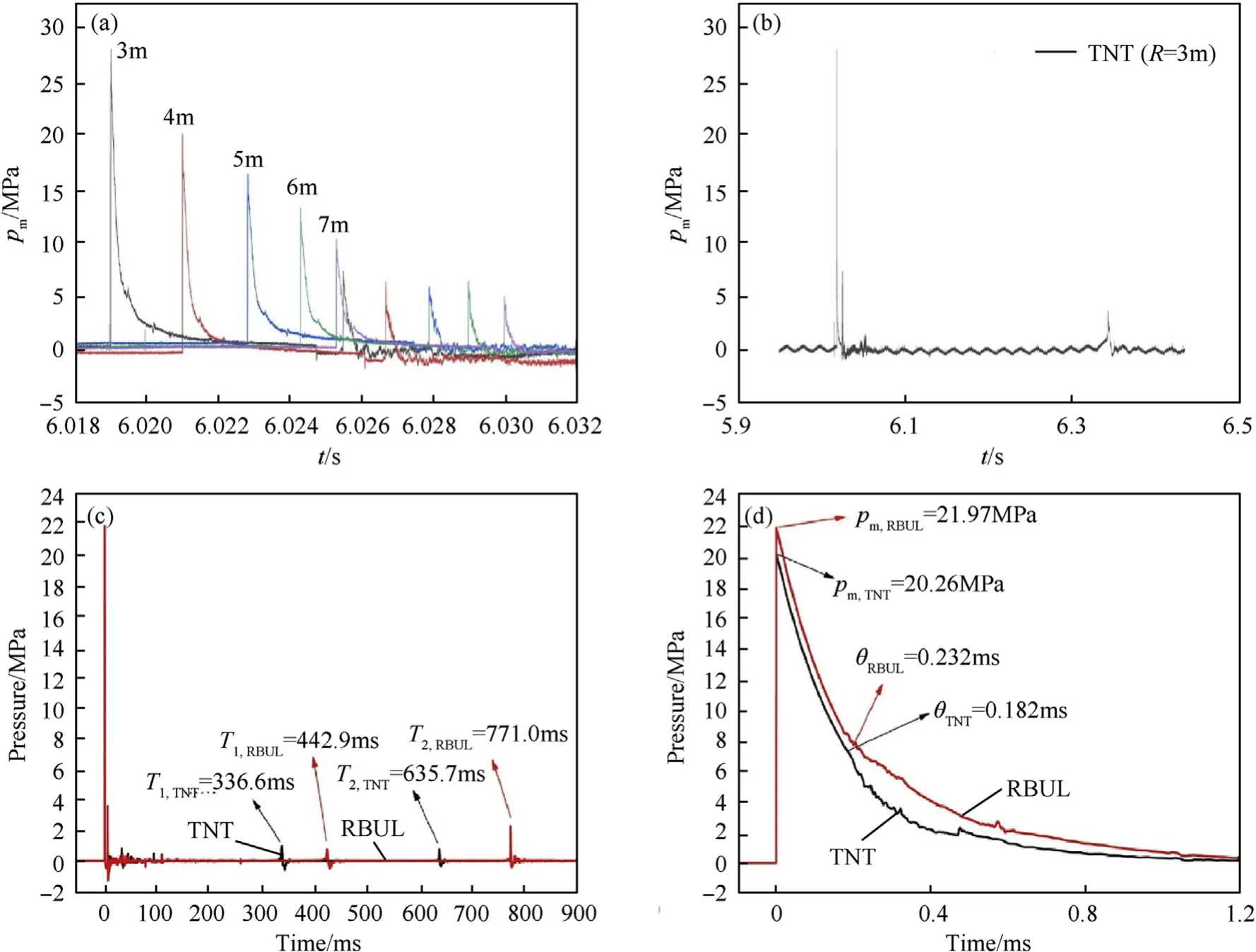
Fig. 2. Pressure signals of the underwater explosion loading. (a) Pressure time history curves of TNT at different stand-off distances (W=5 kg); (b) Pressure time history curve of TNT(W=5 kg,R=3 m);(c)Comparisons of TNT and RBUL shock wave and bubble pulsation pressure history time curves;(d)Comparisons of TNT and RBUL shock pressure history time curves within 7θ(Experimental data has been replaced by an exponential fit. W=5 kg, R=4 m).

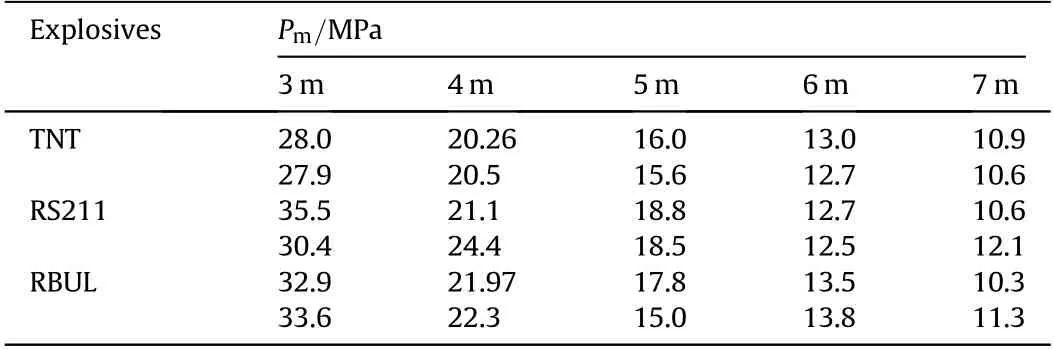
Table 2 Shock wave peak pressure of measured results.

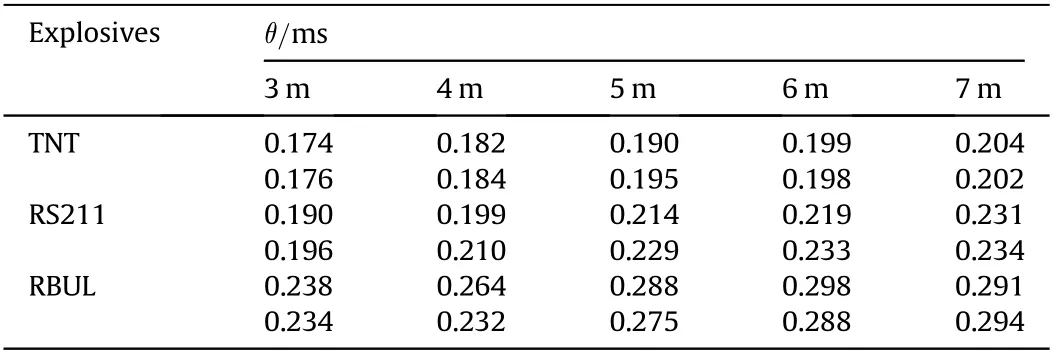
Table 3 Shock wave pressure time decay constants of measured results.

Here K1and A1are constants that depend on the charge type;W is the weight of the charge; R is the stand-off distance from the charge at which the pressure is measured.

Another parameter of the underwater pressure loading is the time decay constant θ expressed by the following empiricalformula:

Table 4 The energy properties of explosives underwater explosion.

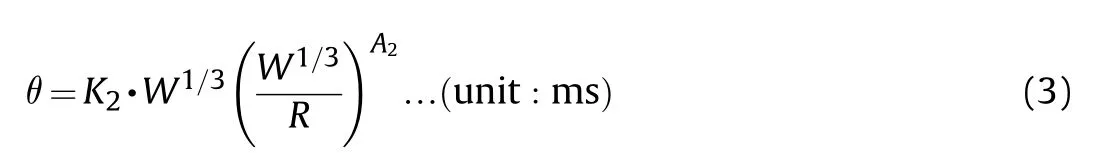
Here K2and A2also depend on the type of charge.

On the basis of a large number of experimental results, the empirical formula has been summarized, which can describe the loading of underwater explosion shock wave better.The expression is as follows:

Eq. (4) is taken the logarithm:

Eq. (5) shows that the logarithm of the underwater explosion loading (Pmand θ/W1/3) is the straight line with a slope of α for ln R,and the absolute value of the slope is α.And K can be obtained by the intercept of the line with the Y axis. The expression is as follows:

The linear distribution is characterized by the linear correlation coefficient r2. It can been clearly seen from Fig. 3 that the linear correlation coefficients of Pmand θ of the two tested aluminized explosives are smaller than those of TNT.That is to say the loading of RS211and RBUL has a larger deviation from the values calculated by the empirical formula. In addition, the linear correlation coefficients of the shock wave pressure are larger than those of the time constants.

The four constants of the three types charges in Eq. (2) and Eq.(3) are obtained by fitting and the results are as shown in Table 5.

The underwater explosion consists of shock wave and bubble pulsation.Geers,Hunter[21,22]selected the time separation point between the shock wave phase and the bubble phase as 7θ.Therefore, it is necessary to establish a suitable description of the shock wave pressure within 7θ.

Table 5 Constants of the three types of charges in Eq. (2) and Eq. (3).

Due to the characteristic that the shock wave pressure of the aluminized explosives attenuates slowly, it is more suitable to use the double exponential decay model to describe the shock wave pressure within 7θ. The double exponential decay expression is as follows:

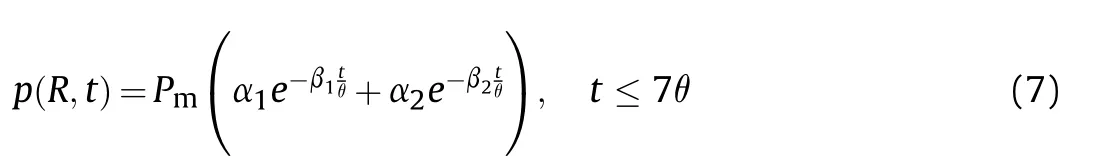
Here α1,β1,α2and β2are constants.

Shock wave pressure p（R，t） is the function of the time (t). The comparison results of single, double exponential fitting and experimental data are shown in Fig. 4. It can be found that the shock wave pressure is in good agreement with the experimental results within 1θ described by the single exponential decay model.However,the double exponential model is in good agreement with the experimental results from 1θ to 7θ.

As shown in Table 6, the values of the four constants can be obtained from fitting by the experimental data.So these constants can be combined with Eq. (2) and Eq. (3) to yield the pressure profile at other distances.

3. The responses of the air-backed plate

3.1. Taylor plate theory

As is shown in Fig.5,when the incident shock wave pincaffects the air-backed plate which density is ρsand thickness is h, the velocity response of the plate is u according to the Taylor plate theory [23].

Fig. 3. The linear correlation coefficients of experimental underwater explosion loading (Pm and θ/W1/3) with stand-off distances. (a) TNT; (b) RS211; (c) RBUL.

Fig. 4. Comparisons of single, double exponential decay and experimental curves. (a) RS211 (W=5 kg, R=4 m); (b) RBUL (W=5 kg, R=3 m).

Table 6 Constants of RS211 and RBUL in the double exponential model.

Here ρwand cware the density and sound speed of the water,respectively.

When the incident wave is described by the single exponential model,the velocity and pressure response formulas are as follows.

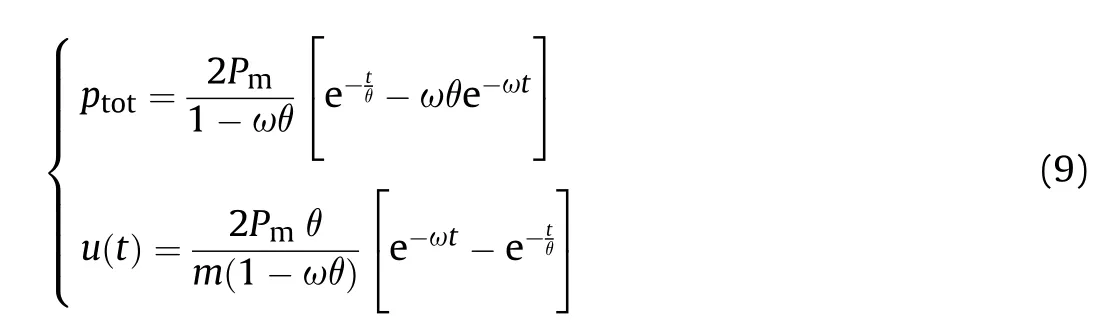
Where,ω =ρwcw/（ρsh）, m =ρsh.

If the incident wave is described by the double exponential model, then Eq. (8) will be written as:

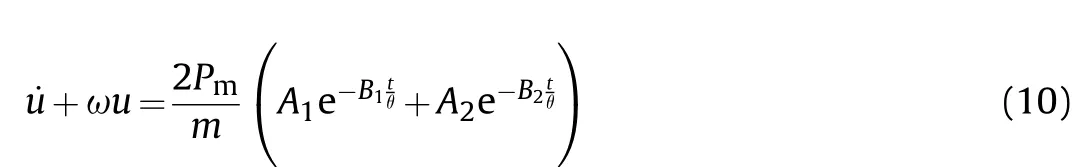
Eq.(11)and Eq.(12)are the responses(velocity and pressure)of the plate:

In a short time, total pressure ptotattenuates to the negative value. Since the fluid can hold over very small tensile stress, local cavitation occurs near the plate. When the local cavitation occurring, the plate reaches the maximum velocity, which is called the kick-off velocity.For the single exponential model[23],the kick-off velocity of the plate can be expressed as follows:

Where β =ωθ.The time when the plate reach the kick-off velocity is tm:

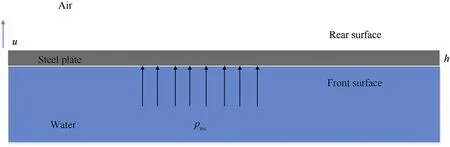
Fig. 5. The schematic diagram of air-backed plate structure.

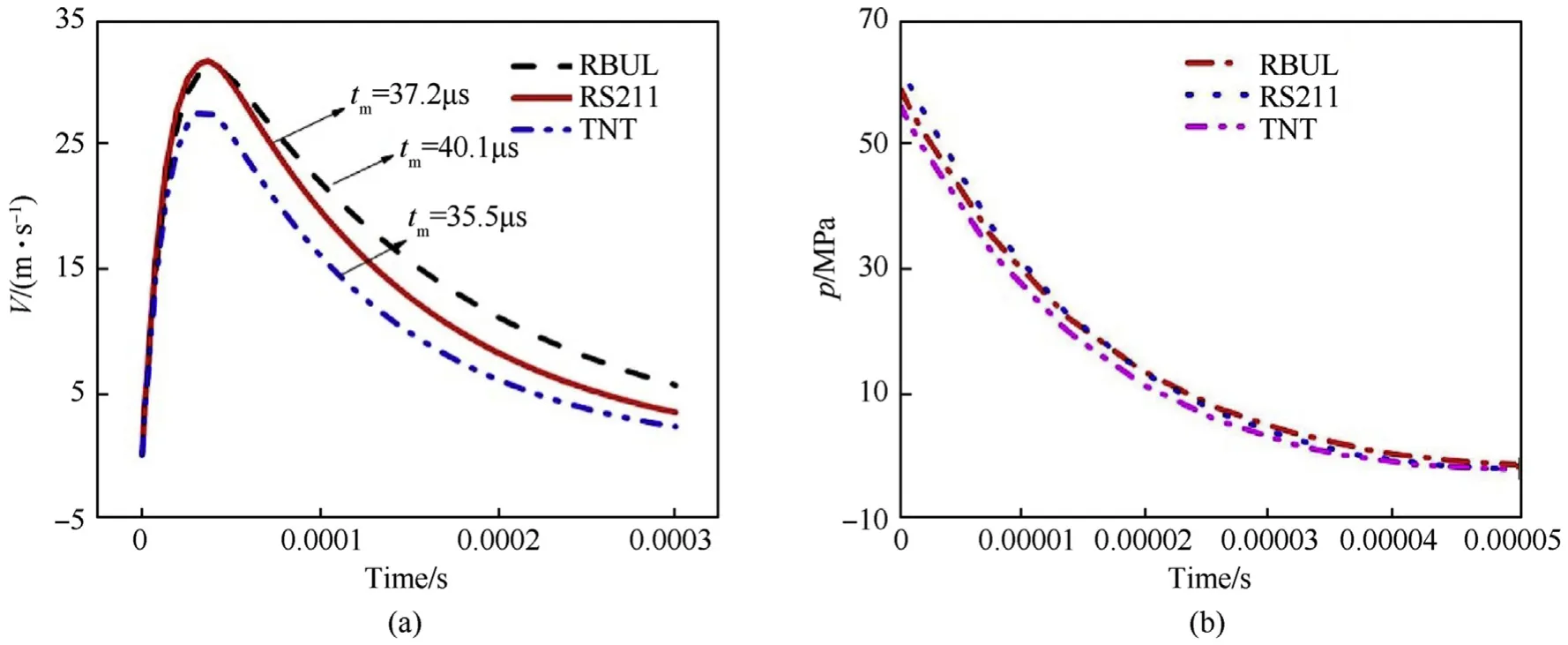
Fig. 6. Comparison of the responses of the air-backed plate (W=5 kg, R=3 m, h=10 mm) (a) Velocity response; (b) Pressure response.

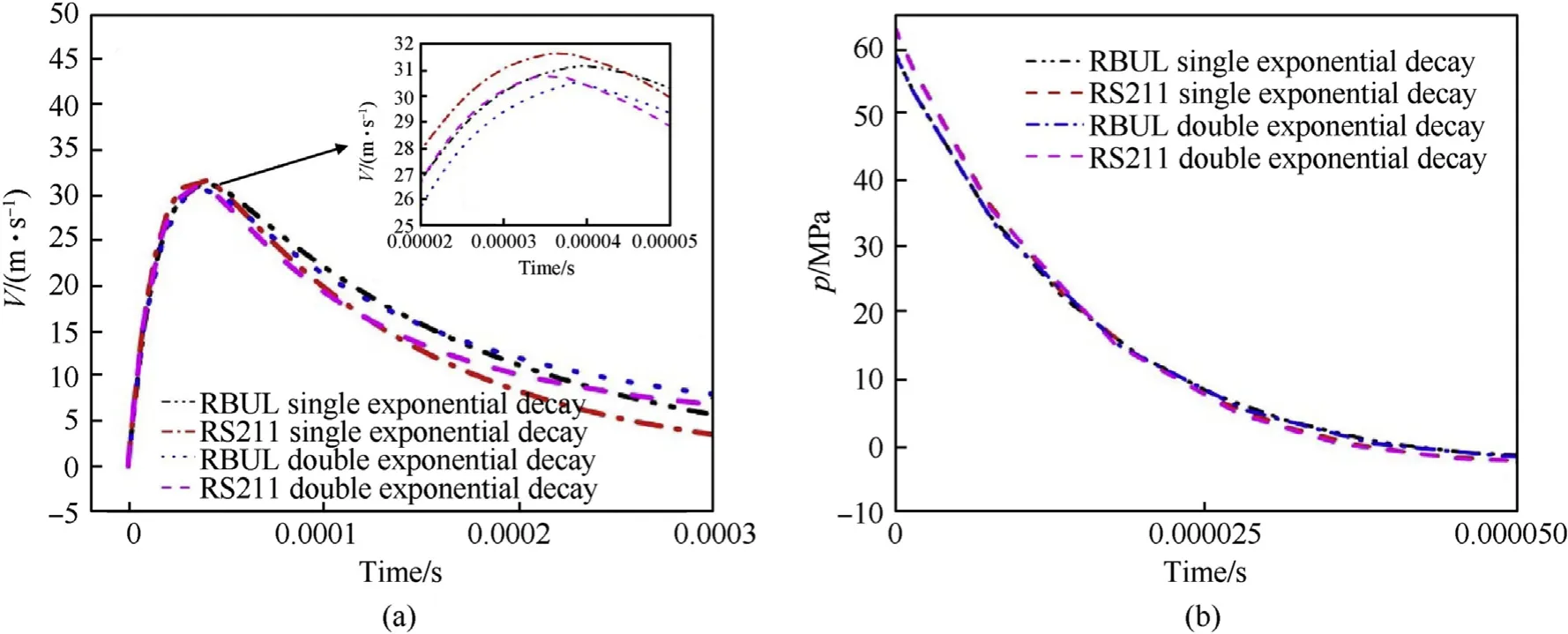
Fig.7. Comparisons of the single and double decay exponential on the responses of the air-backed plate.(W=5 kg,R=3 m,h=10 mm)(a)Velocity response;(b)Pressure response.

Table 7 Kick-off velocity of the plate (W=5 kg, R=3 m).

In Eq.(14),it can be calculated that<1 and θ> tm.That is to say that the time to reach the kick-off velocity is within 1θ.

There are many factors that will lead to the differences and uncertainties in the responses of the air-backed plate. However,only Pmand θ are considered in the early responses of the plate.So if the functional relationship is [24]:

Eq. (15) is fully differentiated:

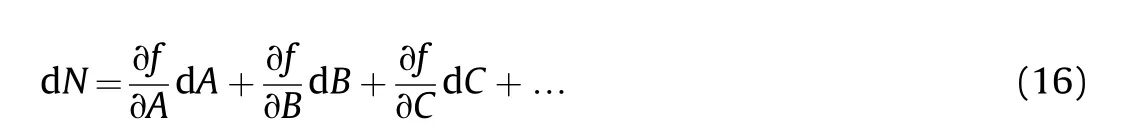
So the formula of the relative uncertainty is:

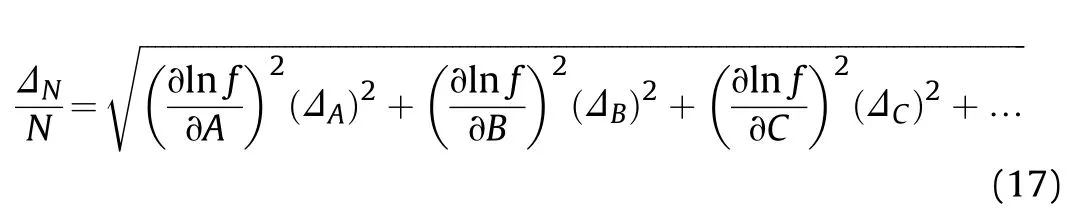
Therefore, according to the relationship of uncertainty in the error analysis theory, the relative uncertainty in the kick-off velocity of the Taylor plate caused by the shock wave peak pressure and time constant(Pmand θ) is as follows:

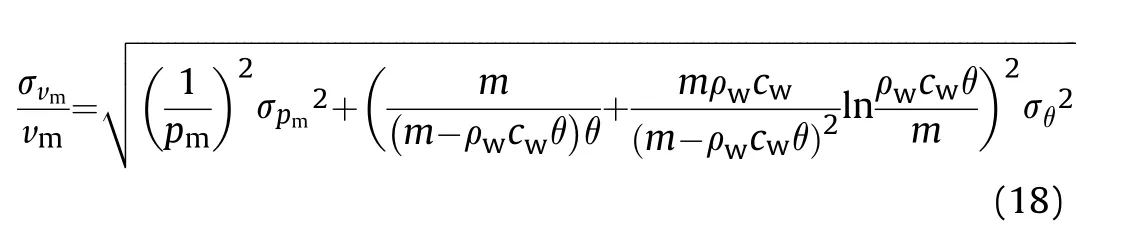
Vmis the kick-off velocity of the air-backed plate.

σvmis the absolute uncertainty of the kick-off velocity of the plate;

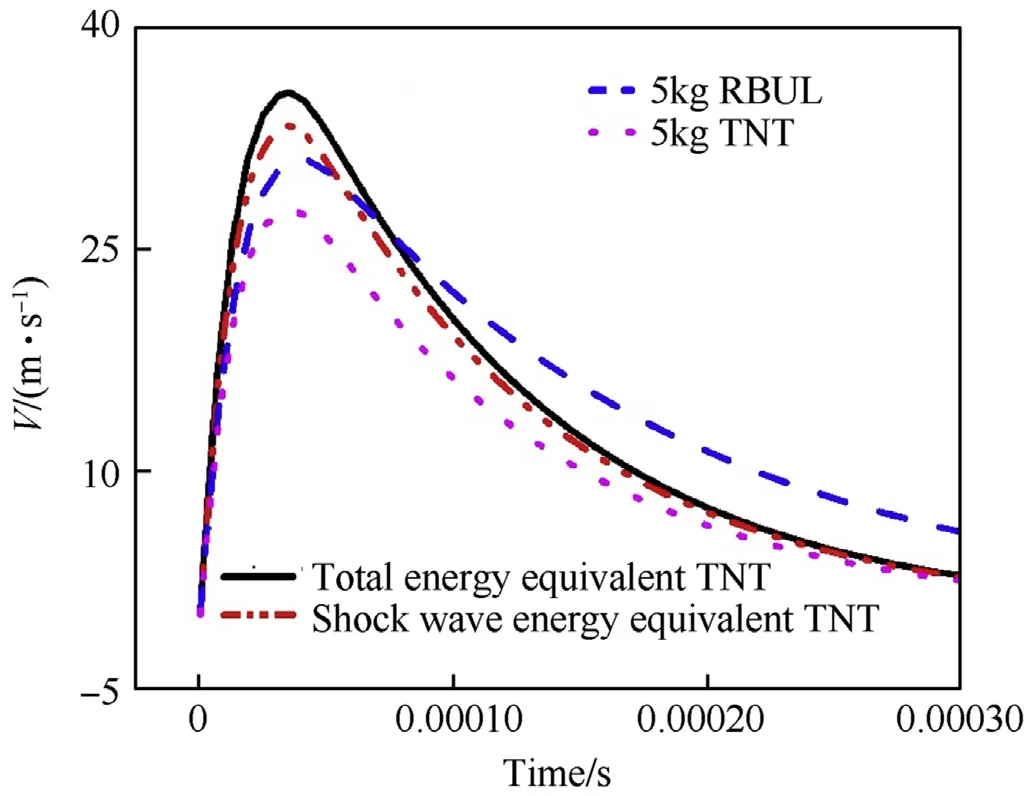
Fig. 8. Velocity responses of the air-backed plate for equivalent explosives.

σpmis the difference between the peak value of the shock wave pressure measured with the empirical value calculated by Eq. (2);

σθis the difference between the time decay constant measured value measured with the empirical value calculated by Eq. (3).

3.2. The effects on the early responses of air-backed plate

3.2.1. Effects of decay model

In this study, it is assumed that the thickness of the air-backed steel plate is 10 mm [4,6,12,25], m = 78.5 kg/m2, ρw=1000kg/m3,cw=1449m/s.And the results of the steel plates withother thickness are similar. If the underwater shock wave is expressed by the single exponential decay, the theoretical responses (velocity and pressure) of the air-backed plate are as follows:

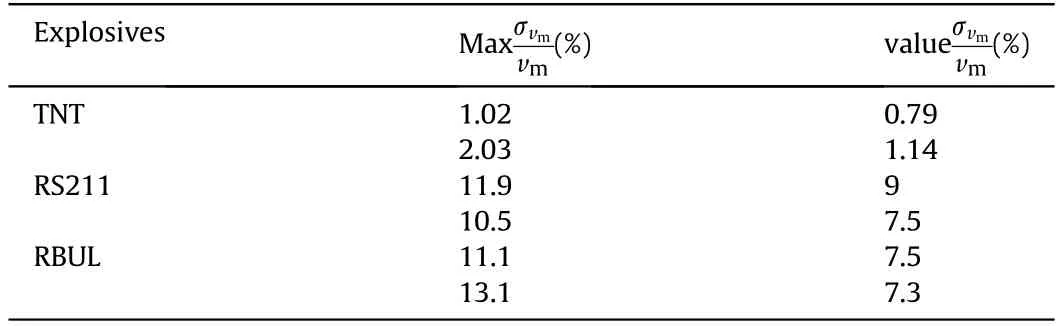
Table 9 Uncertainty in the Response of Air-Backed plate.

As is shown in Fig. 6 (a), the time when the air-backed plate reaches the kick-off velocity is about 30-40 ms. And it is also verified that tm<θ (from Table 3). Vmand tmproduced by the loading of the tested aluminized explosives are always higher than those produced by the loading of the TNT. In addition, the kick-off velocity and the maximum pressure of the plate produced by the RS211 are slightly higher than those produced by RBUL according to Fig. 6(b).

The shock wave pressure could also be expressed by the double exponential decay, which may lead to some differences to the responses of air-backed plate. According to Eq. (11) and Eq. (12), the responses (velocity and pressure)of the plate can be obtained.

It can be naturally found from Fig. 7 and Table 7 that since the generated time of the local cavitation is within 1θ, the kick-off velocity and pressure are approximate calculated by the single exponential decay and the double exponential decay.However,the plate velocities obtained by the double exponential decay are less than that obtained by the single exponential decay in the initial stage. But the results are opposite later.

Table 8 Comparisons of the kick-off velocities of the plate of equivalent methods.

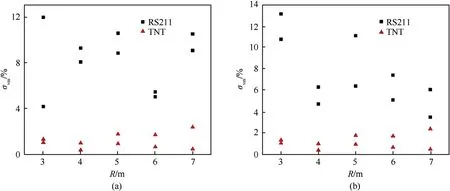
Fig. 9. Comparisons of uncertainties in the kick-off velocities response of air-backed plate at different stand-off distances. (a) Comparisons of TNT and RS211; (b) Comparisons of TNT and RBUL.

3.2.2. Assessment of equivalent method

Underwater weapons is a common application for aluminized explosives. For underwater explosion, only TNT is considered or substituting TNT for aluminized explosive simply in theoretical analysis and numerical calculation. However, due to the special energy output characteristic of the tested aluminized explosives,the velocity responses of the structure may not be accurately obtained by different equivalent methods. So it is necessary to evaluate the equivalent methods.

As is shown in Fig. 8 and Table 8, for the RBUL (W=5 kg,R=3 m), the shock wave energy, mass equivalent and the total energy equivalent method are used,respectively.The values of the kick-off velocity are different calculated by 3 equivalent methods.For example, if the total energy equivalent method is adopted, the difference in the kick-off velocity of plate will be up to 15.8%under the same total energy of TNT explosive, which is worth adopting different equivalent methods.

3.2.3. Uncertainty in response of air-backed plate

According to the experimental data, the underwater explosion loading of the tested aluminized explosives is difficult in accordance with the underwater explosion similarity. For example, the value of peak pressure(Pm)and the time decay constant(θ)will be different with the same weight and stand-off distance. And the difference is random. When the loading of aluminized explosives affects the air-backed plate, the responses of the plate will have some uncertainties. Compared the measured data with the calculated values according to Eq.(2)and Eq.(3),and combined with Eq.(18), the relative uncertainties in the kick-off velocity response of the air-backed plate are obtained. The results are as follows:

As shown in the above Fig.9 and Table 9,it can be obtained that the uncertainties of the ideal explosive TNT on the kick-off velocity response of the air-backed plate are about 1%. However, the underwater explosion loading of the two tested aluminized explosives all have much larger uncertainties in the response of the air-backed plate than those of the TNT.

4. Conclusions

According to the results of underwater explosion experiment,the characteristics of underwater explosion loading of RS211 and RBUL were obtained. It can be clearly seen that there are greater discrepancies between measured values of and the empirical values(Eq.(2)and Eq.(3))for RS211 and RBUL, the energy output modes of which are also different from TNT.The double exponential decay model was proposed to describe the underwater explosion shock wave pressure of the tested aluminized explosives.And it is found that it is in better agreement with the experimental results from 1θ to 7θ than single exponential decay model. Based on the characteristics, the effects on the early responses of the air-backed plate were analyzed.The results indicate that the single-exponential and double-exponential decay models have little effect on the kick-off velocity of the plate because the time to reach the kick-off velocity is within 1θ.Then,the equivalent methods were also evaluated.In case of substituting TNT for aluminized explosives, different equivalent methods may have different impacts on the responses of the air-backed plate. For example, if the total energy method is adopted, the error of the kick-off velocity will be up to 15.8%. The underwater explosion loading of RS211and RBUL has a larger deviation from the empirical formula than that of TNT. The characteristics will cause greater uncertainties in the early responses of the air-backed plate.

Declaration of competing interest

We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work,there is no professional or other personal interest of any nature or kind in any product, service and/or company that could be construed as influencing the position presented in,or the review of, the manuscript entitled, “The Early Responses of Air-Backed Plate Subjected to Underwater Explosion with Aluminized Explosives”.

Acknowledgments

This paper is supported by the project of State Key Laboratory of Explosion Science and Technology(Beijing Institute of Technology).The project number is NO. QNKT19-04.