Optimal design of a novel cylindrical sandwich panel with double arrow auxetic core under air blast loading

Xu-ke Lan, Qi Huang, Tong Zhou, Shun-shan Feng

State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China

Keywords:Auxetic structure Blast response Finite element analysis (FEA)Optimal design

ABSTRACT The increasing threat of explosions on the battle field and the terrorist action requires the development of more effective blast resistance materials and structures. Curved structure can support the external loads effectively by virtue of their spatial curvature.In review of the excellent energy absorption property of auxetic structure, employing auxetic structure as core material in curved sandwich shows the potential to improve the protection performance. In this study, a novel cylindrical sandwich panel with double arrow auxetic (DAA) core was designed and the numerical model was built by ABAQUS. Due to the complexity of the structure, systematic parameter study and optimal design are conducted. Two cases of optimal design were considered, case1 focuses on reducing the deflection and mass of the structure, while case2 focuses on reducing the deflection and increasing the energy absorption per unit mass. Parameter study and optimal design were conducted based on Latin Hypercube Sampling (LHD)method, artificial neural networks (ANN) metamodel and the nondominated sorting genetic algorithm(NSGA-II).The Pareto front was obtained and the cylindrical DAA structure performed much better than its equal solid panel in both blast resistance and energy absorption capacity.Optimization results can be used as a reference for different applications.

1. Introduction

Nowadays,the increasing threat of explosions on battle field and terrorist action requires the development of more effective blast resistance materials and structures. Metallic sandwich structures with a cellular core such as honeycomb,foam and corrugated plate have attracted much attention as they have the capability to mitigate shock and impact by progressive local crushing of its microstructure while still light in weight [1-4].

Different from the cellular material used in the sandwich structures,Negative Poisson’s ratio materials(as known as auxetic materials) show an interesting property as they contract laterally under compression and expand when stretched [5]. With such mechanical behaviors, they show enhanced performances in fracture toughness, indentation resistance, shear modulus and vibration absorption[6-12].Therefore,in recent years,many 2D and 3D auxetic structures have been designed for impact and blast resistance. The most common used structure is re-entrant auxetic honeycomb, and double-V auxetic structures which are easy to manufacture. Imbalzano et al. compared the blast resistance of 2D re-entrant auxetic and honeycomb sandwich panels and numerically studied the blast response of 3D re-entrant auxetic composite panels [13,14]. Wang et al. designed a novel sandwich panel with double-V auxetic structure core,and numerically studied the blast response[15].Qi et al.experimentally and numerically studied the impact and close-in blast response of auxetic honeycomb-cored sandwich panels [16]. Jin et al. focused on graded effect of auxetic honeycomb cores on the dynamic response of sandwich structures under blast loading [17].

All these structures deigned in above studies are based on flat plate. In practice, many facilities and engineering structures are curved,such as high-speed rails,aerospace vehicles,marine vessels and civil infrastructures[18].The curved structures can support the external loads effectively by virtue of their spatial curvature [19].Therefore, researchers combined the advantages of curved panels with cellular core sandwich structures to design blast resistance structures [20-22]. And the curved sandwich panels with cellular material core perform better than traditional flat panels in blast resistance.However,few researches about blast response of curved auxetic panels can be found. Duc et al. analytically studied the nonlinear dynamic response and vibration of sandwich composite cylindrical and spherical panels with auxetic honeycomb core layer[23,24].In our previous study,a cylindrical sandwich structure with 2D re-entrant honeycomb cores was designed, and the negative Poisson’s ratio (NPR) effect occurred only in one direction [25].

To design a cylindrical sandwich core with NPR effect in two directions, a novel cylindrical 3D double arrow auxetic (DAA)structure is developed in this study. Since the curved auxetic structure is complex and highly nonlinear, no direct relations between and design variables and objective function can be found.Therefore, metamodel was employed to solve the objective function when the design variables were given. Several works in seeking the optimal design of blast resistance structures by using metamodels have been reported [26-28]. Qi has conducted an optimal design of curved metallic sandwich panel using artificial neural network metamodel [29]. Wang has employed Gaussian process metamodel to optimal the blast response of a double-V auxetic flat panel [15]. However, up to the present, no optimal design works about curved sandwich panel with auxetic cores can be found.

In this paper, a novel cylindrical sandwich panel with threedimensional DAA structure core was proposed for air blast resistance purpose,and the numerical model was built by ABAQUS.Two cases of optimal design were considered, parameter study and optimal design were conducted based on Latin Hypercube Sampling (LHD) method, artificial neural networks (ANN) metamodel and the nondominated sorting genetic algorithm(NSGA-II).Finally,the Pareto front was obtained which can guide the design of the anti-blast structures.

2. Cylindrical sandwich panel with DAA structure core

Based on the three-dimensional DAA structure, a novel cylindrical sandwich is proposed in this paper. As illustrated in Fig.1, a DAA unit is constructed by eight cylindrical rods, three layers of units are rigidly connected to contribute the whole DAA core. The DAA core is sandwiched by two face sheets to form a cylindrical panel.The panel has a radius of curvature R at the center line of the core, the length and width are both set to be L=W=320 mm, the height of the core layer is H=15 mm,and the thickness of the face sheet is Tf=0.8 mm. In this study the DAA core is weld to the top and bottom face sheets.

Before parametric optimization, in order to select the appropriate parameters as variables, it is essential to understand the relations between geometric parameters. There are three layers of the DAA core,while the number of units along L-line and C-line are NLand NCrespectively. Geometrically, a three-dimensional DAA unit is composed by two two-dimensional DAA units at L and C planes.As show in Fig.2,due to the symmetry,the cylindrical DAA structure has five parameters:three radiuses of curvature R1,R2,R3,and ϴat L-plane;one parameter, width w=L/2nLat C-plane, and the diameter d of the cylindrical rod.The height ratio k is defined as k =（R3-R1）/（R2-R1）.Each layer has the same height ratio k,thus the height of each layer can be expressed as h = H/（2k+ 1）. The volume of the a DAA core at layer i can be expressed as Vi-layer=VC-plane+VL-plane.Where VC-planeand VL-planeare volume of rods at C-plane and L-plane, which can be calculated by the cosine theorem as follows:

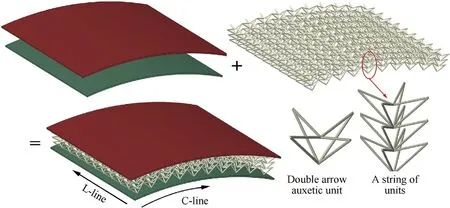
Fig.1. Schematic design of a novel cylindrical sandwich panel with DAA structure. core.

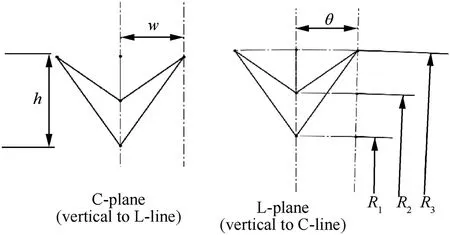
Fig. 2. Geometric parameters of a DAA unit along L-line and C-line.

Fig. 3. Boundary conditions and Conwep blast loading in FE model of a quarter cylindrical sandwich panel with DAA core.

Thus,when the five parameters:R,k,d,NLand Ncare given,R1,R2, R3can be calculated in each core layer according to Fig. 2, and the mass of the DAA core can be obtained as:

Where ρbaseis density of base material.Therefore,in this study R,k,d,NLand NCare selected as the optimized parameters in section 4.

3. Numerical modeling

3.1. Symmetrical model for cylindrical DAA panel

In this paper,the air blast response of sandwich panel with DAA core was researched by employing ABAQUS/Explicit as a numerical solver, which is reliable for complicated nonlinear dynamic problems.As shown in Fig.3,due to the symmetry of the model,only a symmetrical quadrant of the cylindrical DAA panel is modeled in order to improve computational efficiency. Symmetrical boundary conditions are imposed on the C-symmetry plane an L-symmetry plane,while being fixed on the other two sides.The face sheets are modeled by using ABAQUS shell element S4R element(the 4-node doubly curved general-purpose, reduced integration, hourglass controlled,finite membrane strain shell element),and the DAA core is modeled by B32 element(three-node second-order Timoshenko beam elements). The top and bottom layer of the core are weld to the front face sheet and back face sheet using tie constrains. General contact algorithm in ABAQUS provide an efficient way to define contact in complex models.The contacts between the core and face sheets,as well as the self-contact of the DAA core are considered by using general contact.

Batch calculation in the optimization requires the model to have a high computational efficiency. Therefore, a mesh sensitive study and a contact convergence study were performed, which indicate that model with B32 element mesh size of 0.5 mm and frictionless general contact can balance the calculation accuracy with the calculation efficiency. Therefore, all contacts are considered frictionless and element size of B32 is set as 0.5 mm while the mesh size of S4R is set as 1 mm. The numbers of elements and nodes varied largely depends on the geometric parameters. A typical model includes 50482 nodes and 56416 elements(R=460,k=1.77,NC=24,NL=19).

3.2. Blast modeling

In this study,a lot of numerical simulations are need.If the real charge is simulated, it is necessary to build a Euler filed, which is computationally expensive. Therefore, the air blast loading was generated by employing the CONWEP (conventional weapons effects program) empirical model, which does not require a Euler field, and the calculation of the applied load by empirical formula can greatly reduce the calculation cost. The CONWEP algorithms[30] developed by Kingery and Bulmash account for angle of incidence by combining the reflected pressure (normal-incidence)value and the incident pressure (side-on-incidence) value. The pressure can be calculated by the following equation:

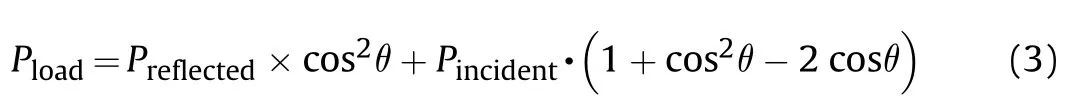
Where θ is the angle of incidence;Pincidentis the incident pressure;Preflectedis the reflected pressure. CONWEP model available in Abaqus/Explicit has two parameters: the equivalent mass of TNT and the standoff distance. In this study, 30 g TNT was used as the explosive with a 100 mm standoff distance away from the center ofthe sandwich panel.

Table 1 Material properties and Johnson-Cook parameters of 5038-H116 aluminum alloy[14].

3.3. Material properties and modeling

The whole sandwich panel,including core and face sheets were designed to manufactured from aluminum alloy 5038-H116. This aluminum alloy shows high energy absorption-to-weight ratio due to its low density, high ductility and anti-corrosive properties in comparison with steel alloys.In view of the plastic deformation and strain rate dependence, the Johnson-Cook plasticity, which includes strain hardening, strain rate and temperature effects was employed as a constitutive model in the simulations. According to this model, the flow stress σyis given by Ref. [31].

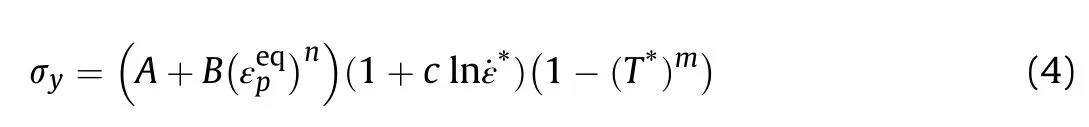
4. Optimization process

4.1. Optimization problem formulation

When deign an auxetic structure, parameter optimization is an essential problem. To simplify the calculation, only the independent parameters of DAA core were optimized while the thickness of the face sheets was set to constant.Five independent parameters of the DAA core were selected as the design variables: R, k, d, NLand NC. The face sheets thickness Tf=0.8 mm and core thickness H=15 mm in all cases. The blast resistance performance of a structure can be evaluated by serval indices. First of all, the maximum displacement(MaxD)of the inner face sheet through the blast process needs to be reduced.In the meantime,the structure is expected to absorb more plastic energy to reduce the kinetic energy. Meanwhile, the mass of the anti-blast structure should be considered because of the requirement of lightweight in mechanical applications. In this study, the optimization problem of cylindrical sandwich panel with DAA core can be mathematically descripted as:

Where SEA=E/m is the specific energy absorption. Case1 focuses on minimizing of both deflection and mass,while case2 focuses on minimizing the deflection and maximizing the specific energy absorption.Only the values within the above reasonable ranges were studied to ensure that the structure is meaningful in practice. A negative Poisson’s ratio effect may not be observed if the parameter is too much deviation from the range, such as NC, NL≤5, k ≤1.While large NC, NL, k, d may result in high density and reduce the calculation efficiency.

4.2. Artificial neural network (ANN) metamodels

In this paper,if the optimization program algorithm was directly implemented on the numerical model, a large amount of performance evaluations was required to formulate objective and constraint functions.Therefore,metamodels was applied instead of expensive FE analysis to improve optimization efficiency. I n this study,the artificial neural networks(ANN)metamodels was used to approximate the relationship between the blast resistance performances and design variables.

Similar to the biological neural system, ANN are formed of a diagram of simple processing elements called neurons that work together to solve problems. ANN has been used widely in optimization problems and has been proven effective and efficient in the design of composite structures. Typical feed forward ANNS has three layers of neurons as shown in Fig.4.Neurons at the input and the output layers represent the input variables (x1～xn) and the response of a system(y1～ym),respectively.And the layer between the input and output layers is a hidden layer, which composed of nonlinear activation functions. wijand wjkare the connection weight between the input layer and the hidden layer, the hidden layer and the output layer,respectively.The ANNS can be written in general form as

where f is the activation functions, ajand bkare constant called‘bias’ neurons, n, l, m are the numbers of neurons of input layer,hidden layer, and output layer, respectively. In this study, the following function y = 1/(1+e-x) was employed as the activation function, which is included in the MATLAB Network Toolbox. The input layer has 5 nodes, the output layer has 2 nodes, and the hidden has about 15 nodes.

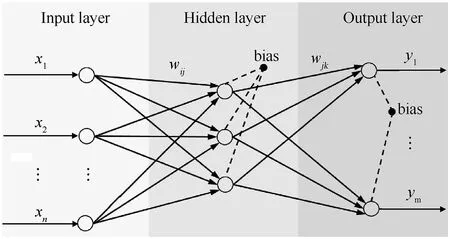
Fig. 4. Schematic diagram of the topology of the three-layer feed forward neural network.

Table 2 Error analysis of ANN metamodels.

Before an ANN can be used, it needs to be trained by using design variables and the corresponding FE results as input and output data. Regardless of the type of applied metamodel, appropriate Design of Experiment (DoE) algorithm should be employed to guarantee the properly distribution of the samples in the design space. DoE aims at representing accurate relations between objective function and design variables with as few samples as possible.Latin Hypercube Sampling(LHD)method was used in this study to generate 200 DoE points filling in a uniform manner in the design space by maximally avoiding the design points of each other.

The quality of the ANN performance was established based on the specified values of errors: maximum absolute error MAX,maximum absolute percentage error MAPE, and R-square calculated by(9)-(11), respectively.

where yiis the FE results,is the mean value ofis the ANN metamodel approximation, and M=200 is the number of DoE points.The values of the three quality indicate are given in Table 2.

The purpose of this study is to find the solutions to a constrained multiobjective problem. Usually, the solutions are a group of best trade-off designs, called “Pareto front” in the feasible domain where all the constrains are satisfied. In this study, the nondominated sorting genetic algorithm (NSGA-II) was used. This algorithm has been successfully used to solve multiobjective engineering optimization problems. NSGA-II has two effective sorting principles: the elitist nondominated sorting and crowing distance sorting, the details can be found in Refs. [32,33].

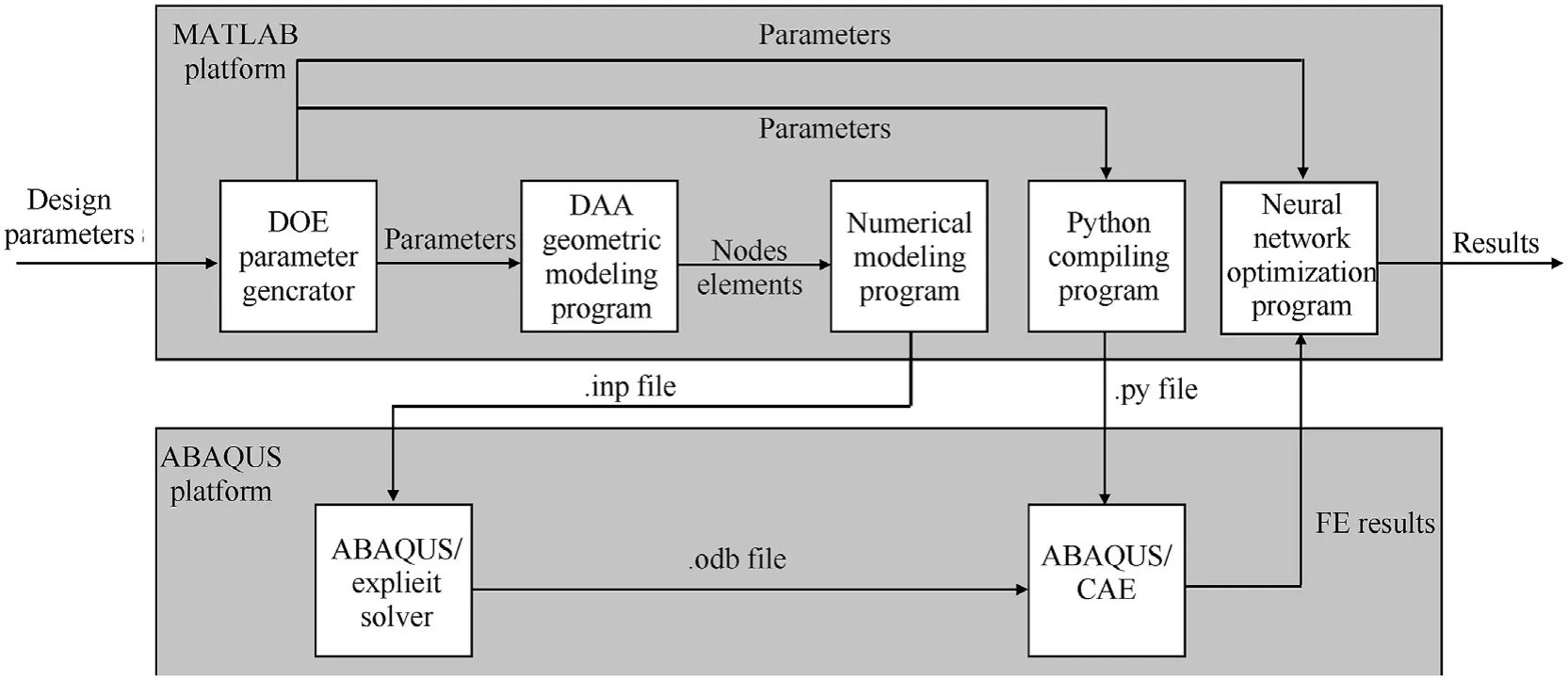
Fig. 5. The flow chart for modeling, solution and optimization of the cylindrical DAA sandwich panel in MATLAB and ABAQUS.

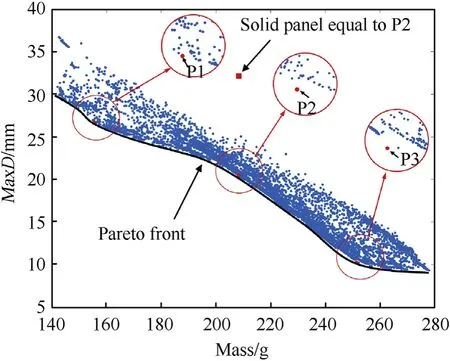
Fig. 6. Optimization design results of case1 study.

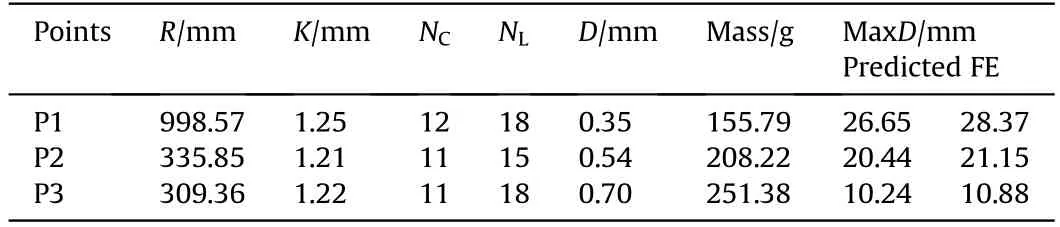
Table 3 Optimum design parameters for case1.

4.3. The interaction between MATLAB and ABAQUS

In order to realize parametric optimization and simplify the process of modeling, MATLAB platform was used in conjunction with the ABAQUS platform.As illustrated in Fig.5,on the MATLAB platform,200 sets of parameters were generated by DoE parameter generator when the ranges of design parameters were given. DAA geometric modeling program calculated nodes coordinates as well as the connection relationship of nodes to form elements.Then,all the information of nodes and elements were written into.inp files through numerical modeling program. On the ABAQUS platform,the.inp files were solved by ABAQUS/Explicit solver and the results were written into.odb files.In order to carry batch post-processing in ABAQUS/CAE,.py files were generated through python compiling program by using the parameters from DoE. Finally, all the FE results were put back into neural network optimization program along with DoE parameters to get the results in form of Pareto front.

5. Results and discussion

Two ANN metamodels for case1 and case2 were built and trained by 200 DoE points and FE results. And the NSGA-II were employed to solve the optimization problem of case1 and case2.The 200 DoE points and FE results were used as the first generation and the genetic algorithm iterated for 50 generations.All the 10000 points were converged in the final results.

5.1. Case1 study

5.1.1. Pareto Front of case1

Fig.6 shows all the 10000 optimization samples,represented by blue points. The Pareto Front can be obtained, which is not the precise front but only a demonstration used black lines. A strong confliction of the maximum enteral deflection and mass of the DAA panel can observed from the Pareto Front. Along the Pareto Front line, the only way to reduce MaxD is to increase the mass of the panel. On the purpose of validate the accuracy of the metamodel,three special points close to the Pareto Front were selected as illustrated in the red circle in Fig.6.The designs of the three points were numerically simulated. The design parameters and the predicted results and numerical simulation results were listed in Table 3.It implied that the prediction of ANN metamodel was close to the FE results. To make a comparison, the blast response of an equivalent solid cylindrical panel with the same curvature,length,width,and mass of points 2 were simulated by using the same blast loading, material, boundary conditions as mentioned in section 3.The deformation process of P2 and the equivalent solid cylindrical panel were shown in Fig.7.And in Fig.6 the panel was represented by a red square which is away from the Pareto Front. The results indicate that the DAA sandwich structure can massively improve the air blast resistance compared with solid panel.

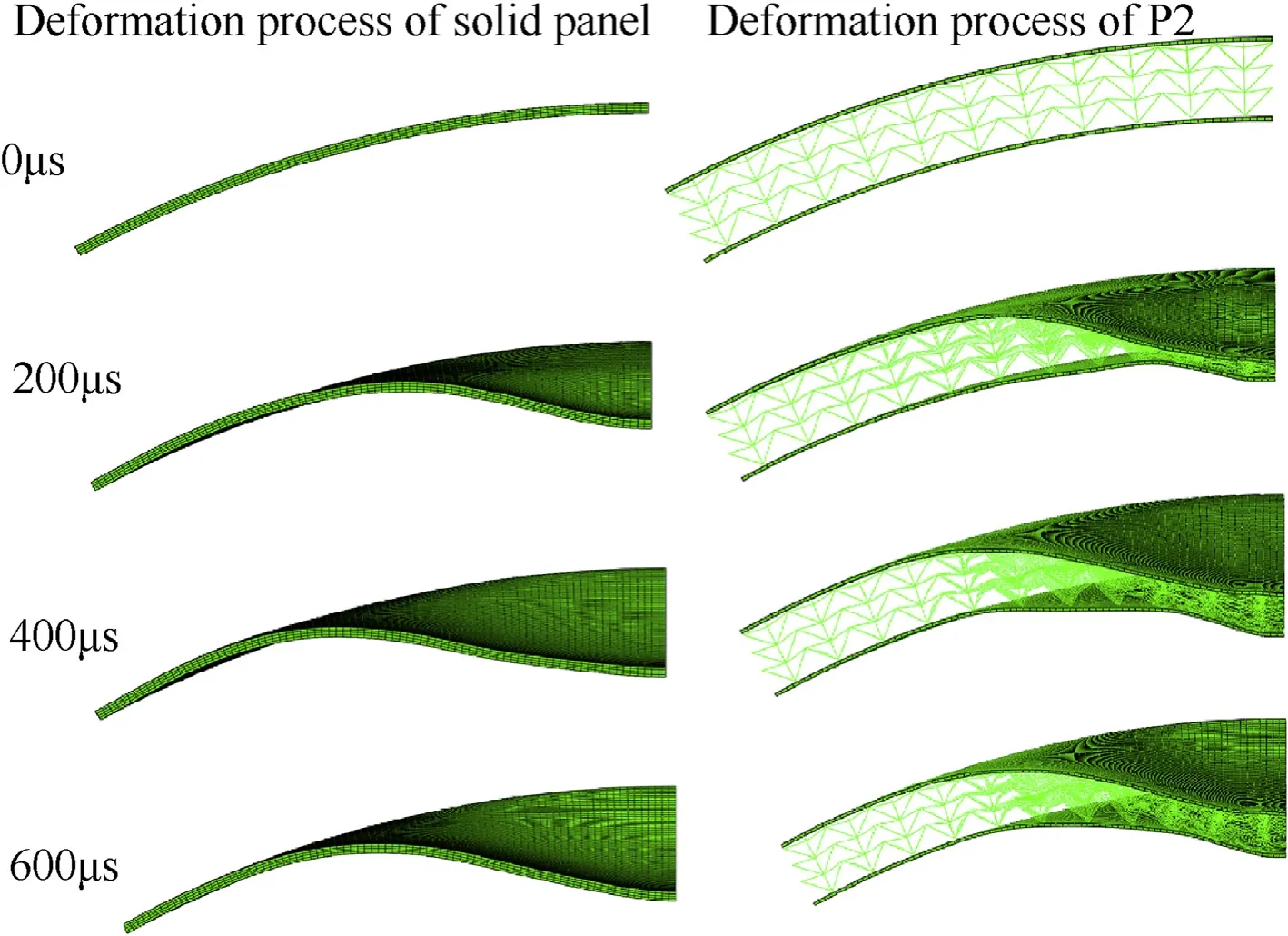
Fig. 7. Comparison of deformation process of solid panel and P2

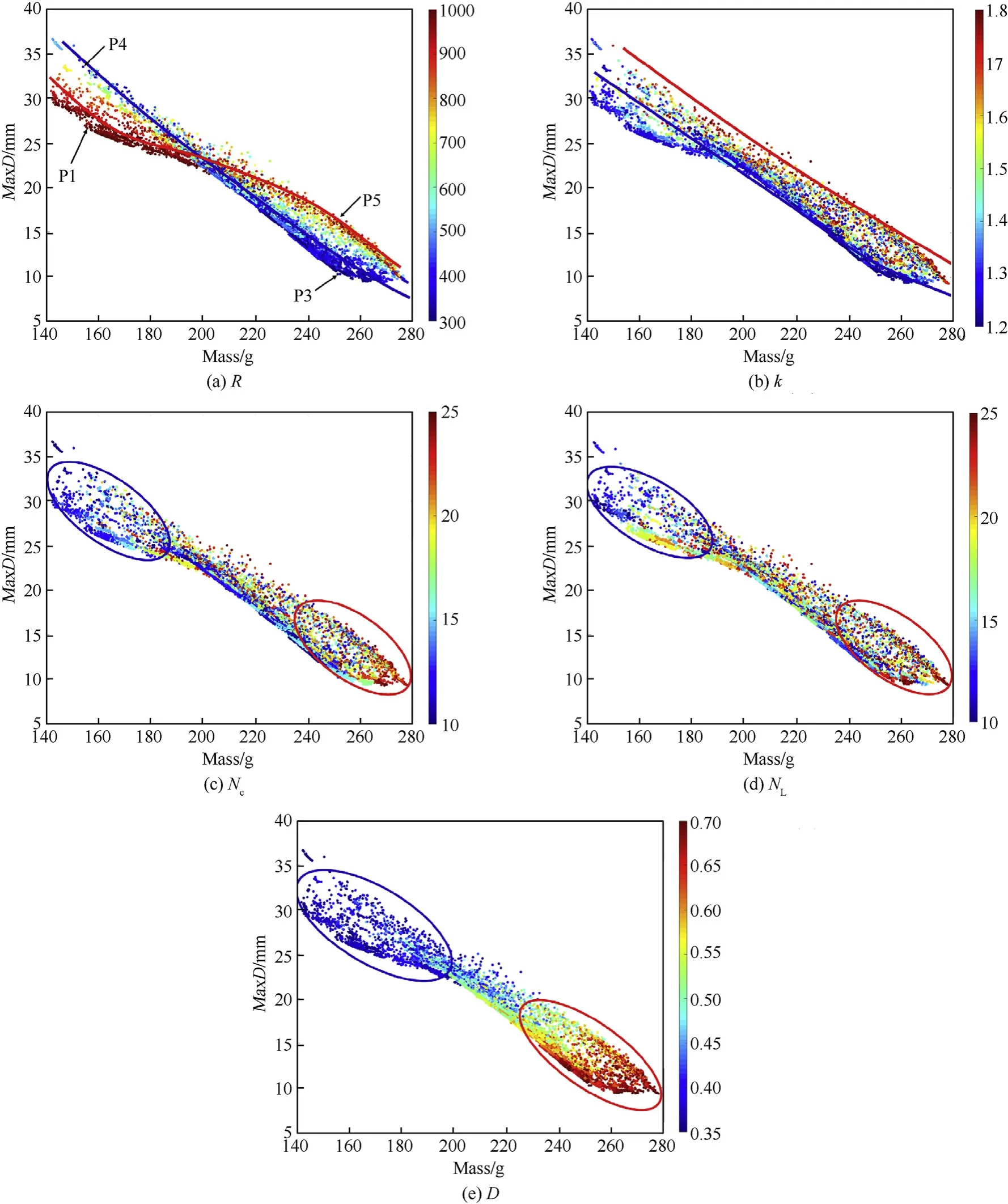
Fig. 8. Scatter plots of the influence of five design parameters: R, k, NL, NC and D.

5.1.2. Parameter study of case1

The influence of design parameters was studied by using scatter plots of all optimization samples points. MaxD vs Mass scatter figures with respect to R, k, NL, NCand D are shown in Fig. 8 respectively. The value of a design parameter is represented by the color of sample points, and can be finding in the color bar at each subplot.As shown in Fig.8(a),the scatter plot can be divided into two regions: a large mass region and a small mass region by two curves. Sample points with small R are distributed along the blue curve, while sample points with large R are distributed along the red curve.In small mass region,red sample points are closer to the Pareto Front than blue points, and in large mass region blue sample points are closer to the Pareto Front than red points. This phenomenon indicates that in the case of a large mass structure,the performance increases as the curvature increases, and in the case of small mass structure,and the performance decrease as the curvature increases. To explain this phenomenon, four points in Fig. 8(a): P1, P3, P4, P5 were selected and simulated, the deformations of the maximum center displacement moment are shown in Fig.9(To make a clearer display of deformation,the mesh display is turned off).

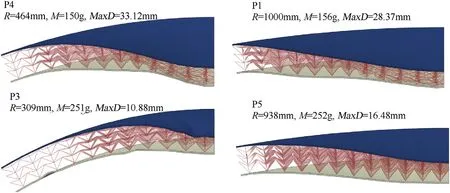
Fig. 9. Snapshots of four sample points in Fig. 8(a) of maximum center point displacement moment.

P1 and P4 have a small mass, most of deformation of P4 is concentrated in the central area, although it has a large curvature the structure cannot disperse the blast impulse effectively.Compared with P4, P1 shows a global bending and compression,the impact energy can be effectively dispersed and absorbed by the whole structure. Therefore, in small mass region, samples with small curvature perform better than samples with large curvature.P3 and P5 have a large mass,by virtue of the curvature,P3 shows an additional stiffness than P5.Under the support of the core layer and the back face sheet,the reflective angle of the reflective blast wave can be changed, and results in a reduction of the blast impulse acting on the front face of sandwich panels. In addition, previous study [25] concluded that, the existence of the curvature can support the negative Poisson’s ratio effect to pull material into the central deformation zone to absorb impact energy and enhance the strength of the structure. Therefore, in large mass region, samples with large curvature perform better than samples with small curvature.

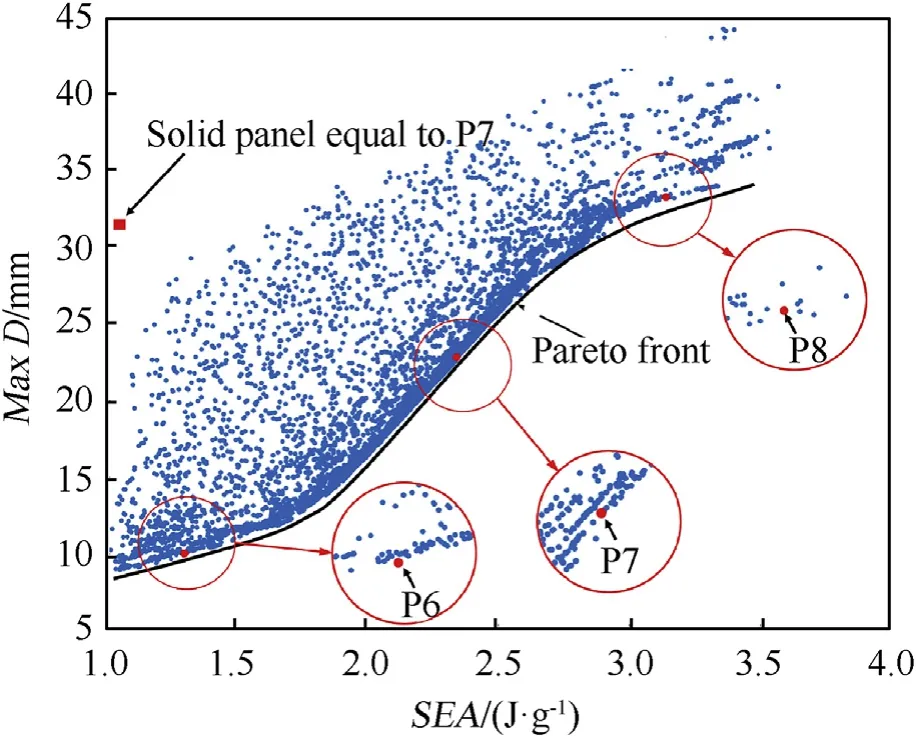
Fig.10. Optimization design results of case2 study.

As shown in Fig. 8(b), as the value of k decrease, the sample points are closer to the Pareto Front. Previous study of 2D double arrow auxetic structure provided that 2D double arrow auxetic structure with a smaller k shows a higher yield strength[34].And the 3D double arrow auxetic structure is composed of two 2D double arrow auxetic structure vertically combined, so its yield strength has a similar variation with the 2D double arrow auxetic structure. Therefore, blue sample points show a greater yield strength and closer to the Pareto Front than red sample points.NL,NCand D show a similar effect on the scatter plot that red points are more appeared in the right large mass region which means that a large value of NL, NCand D can improve the blast resistance performance.

5.2. Case2 study

5.2.1. Pareto Front of case2

Similar with case1 study, Fig. 10 shows all the 10000 optimization samples,represented by blue points.The Pareto Front can be obtained, which is not the precise front and was only a demonstration used black lines. MaxD is positively correlated with SEA.Along the Pareto Front,to increase SEA,a larger MaxD is needed.To validate the accuracy of the metamodel,three special points(P6,P7,P8)close to the Pareto Front were selected as illustrated in the red circle in Fig.10. The designs of the three points were numerically simulated. The design parameters and the predicted results and numerical simulation results were listed in Table 4.

It implied that the prediction of ANN metamodel was close to the FE results. To make a comparison, the blast response of an equivalent solid cylindrical panel with the same curvature,length,width,and mass of points 6 was simulated by using the same blast loading, material, boundary conditions as mentioned in section 3.The result is shown in Fig.10 represented as a red square,which is away from the Pareto Front. It indicates that the DAA sandwich structure can massively improve the SEA by core crushing while keeping a small MaxD, compared with the equal solid panel.

5.2.2. Parameter study of case2

As the same with case1 study, the influence of design parameters was studied by using scatter plots of all optimization samples points.MaxD vs SEA scatter figures with respect to R,k,NL,NCand D were shown in Fig.11 respectively.The value of a design parameter is represented by the color of sample points and can be find in the color bar at each subplot. In Fig.11(a), sample points with small R are distributed along the blue curve,while sample points with large R are distributed along the red curve. And most part of the Pareto Front consist of red points, which indicate that panels with smallcurvature perform better than panel with large curvature. As explained in case1 study,deformation of panel with large curvature was concentrated in the center region of the panel, while deformation of panel with small curvature appeared in almost the whole panel, therefore panel with small curvature has more effective structural mass contributed to the energy absorption which results in a large SEA compared with panel with large curvature.

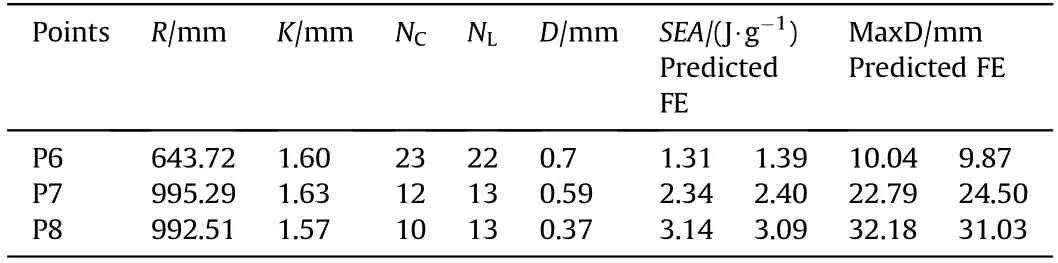
Table 4 Optimum design parameters for case2.

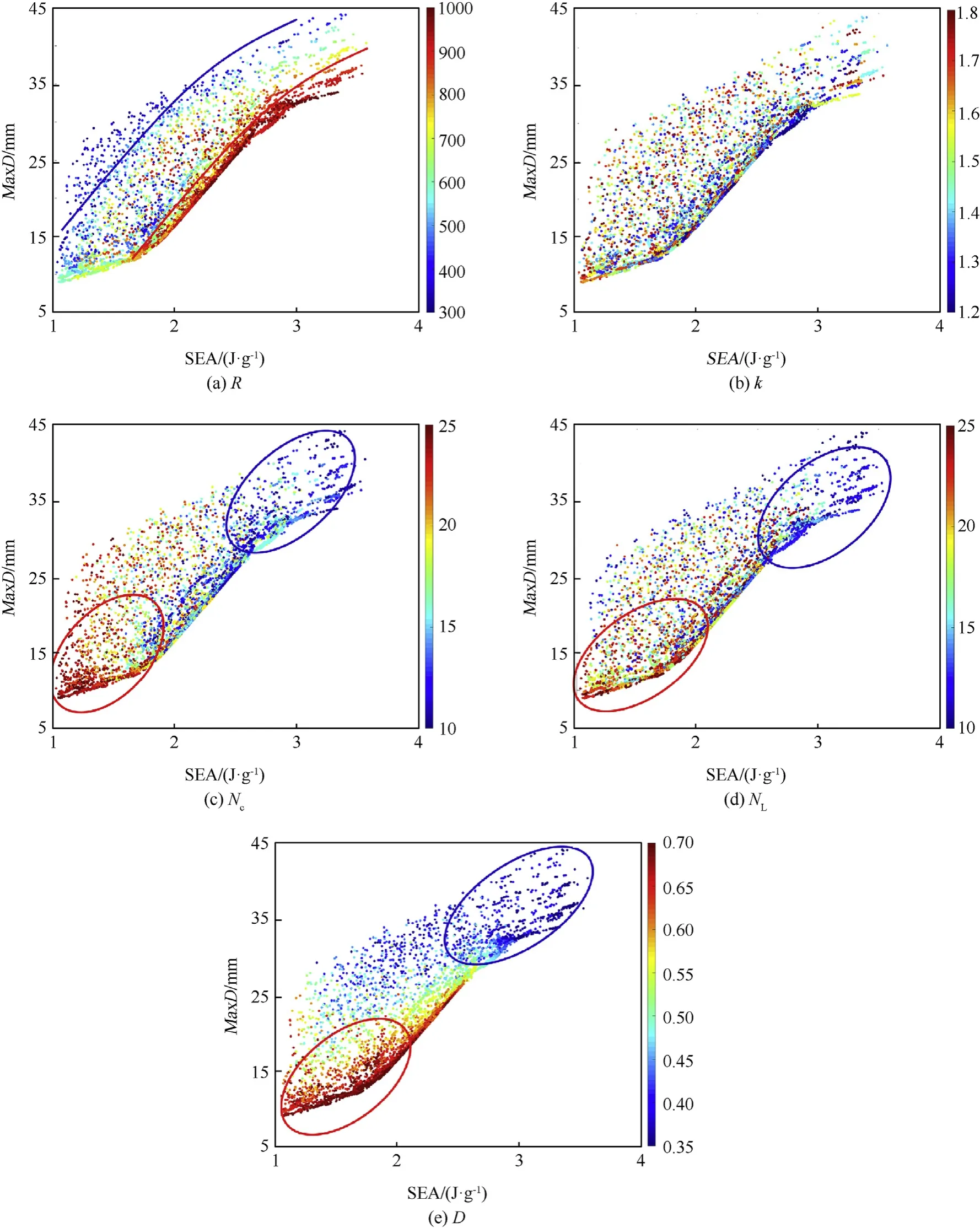
Fig.11. Scatter plots of the influence of five design parameters: R, k, NL, NC and D on case2.

The magnitude of the k value is almost evenly distributed in the scatter plot which means that, the height ratio of DAA core unit shows no significant effect in the optimization design results.NL,NCand D shows similar effects on the scatter plot that red points are more appeared in the region close to the origin of the coordinate while blue points are opposite.A large value of NL,NCand D result in a large value of mass,which is the dominate factor of MaxD and SEA.

6. Conclusion

In this paper, a novel cylindrical sandwich panel with threedimensional DAA structure core was designed for air blast resistance purpose, and the numerical model was built. Two cases of optimal design were considered, parameter study and optimal design were conducted based on the Latin Hypercube Sampling(LHD)method,the artificial neural networks(ANN)metamodel and the nondominated sorting genetic algorithm (NSGA-II). The following conclusions were obtained:

(1). The results proved that the artificial neural networks (ANN)metamodel was accurate by training with 200 DoE sample points. The design parameters can be selected from the Pareto Front based on the specific demand of deflection,energy absorption and mass.

(2). The curvature of the structure plays and import role in the forming of Pareto Front in both case1 and case2 studies. In case1 study, increasing the curvature can improve the blast resistance performance if the structure has a large mass. In case2 study, a small curvature leads to the best trade-off design of structure with efficient energy absorption capacity.

(3). Increasing the height ratio k of DAA core can improve the blast resistance performance in case1, while show no significant effect on case2.Structures with large number of core cells and thicker core rods have a large mass which result in reduction in deflection but lose the ability to absorb energy efficiently.

Declaration of competing interest

The authors declared that they have no conflicts of interest to this work.