军事活动影响下的终端区容量评估方法研究

2020-06-27黄海清甘旭升丁黎颖孙静娟

航空工程进展 2020年3期

黄海清，甘旭升，丁黎颖，孙静娟

(1.西京学院理学院，西安 710123)(2.空军工程大学空管领航学院，西安 710051)

0 引言

军事活动作为制约终端区容量评估有效性的关键因素，准确地预测终端区容量对于提高空域管理水平具有重大意义。2010年，由于军用航空活动的限制，兰州管制区内有近320架次的航班受到军事活动的影响，其中航班盘旋最长时间达到40分钟。2014年，东南沿海的军事演习造成了大量的航班延误甚至取消。大量的军用航空活动，对民航航班的飞行造成一定的影响。军事活动已经成为终端区容量的重要影响因素。目前国内对于军事活动影响下的终端区容量评估的研究很少，大多是定性的评估，定量的分析较少。军事活动性质比较特殊，飞行流控时间较长，且占用高度层范围大，需要在各个活动区域内不断穿越高度层，或者在不同的活动区域内相互穿越，因此对活动区域周边的航路航线影响较大；且军事受限区所需要考虑的因素更加多样化，包括天气、飞机偏航、空中风、飞行员操纵等。因此，军事受限区的划设成为一个难点。

目前，国内外对于空域容量的评估方法主要有四种：一是基于数学模型的评估方法；二是基于历史数据的评估方法；三是通过计算机仿真的评估方法；四是通过管制员工作负荷评估的方法。国外，T.R.Inniss等[1]根据危险天气的统计数据来估算对到达容量的影响；J.Krozel等[2]通过圆锥形空域来模拟机场终端区，并给出了短期的确定性容量预测及相应的概率分布；J.Zou等[3]应用最大流和最小割定理来对危险天气影响下的空域容量进行评估；M.Janic[4]利用管制员工作负荷量来评估容量，并研究了不同的空中交通管制操作程序、间隔规则和服务规则对空域容量的影响；P.Volf[5]将扇区空域作为研究对象，通过对管制员工作负荷和管制员承受能力的研究，以管制员可承受的负荷阈值作为限制计算最大的飞行架次。国内，刘欢[6]充分考虑了军用航空影响、天气改变等动态因素，构建了区域动态容量评估模型，并开发出了区域容量评估系统；王少朋等[7]分别从理论和应用方面研究了管制员工作负荷评估，并以此构建了基于管制员工作负荷的区域扇区容量评估模型；杨昌其等[8]基于BP神经网络模型，建立了管制员疲劳状态的识别方法。然而，由于军方活动的特殊性，目前还没有相应的数学模型和历史数据库。国内外对于空域容量的评估方法，大都不适用于军事活动影响下空域容量评估，需要重新构建一套适用于军方活动影响下的评估体系。

国内学者主要利用数学分析法来求解终端区容量。但该方法随着节点的增多，计算的复杂度呈指数型上升，且由于算法本身的限制不适合用计算机进行大规模的编程。

本文将军事活动作为影响因素加入到流量决策当中，利用最大流最小割理论[9-11]从定量的角度求解军事活动影响下的终端区容量，在分析传统算法的特点及缺陷的基础上，用改进的遗传算法求解军事活动影响下的终端区容量，并与传统算法进行比较验证。

1 基本概念

1.1 飞行受限区

飞行受限区就是指当受到恶劣天气、军事活动或者流量控制等因素影响时，为了保障飞行安全在规定时间段内而禁止飞越的空域。

在本文中，将受到军事活动影响的区域作为飞行受限区，民航航班在飞行过程中不得在该区域内通过。

1.2 终端区动态容量

终端区动态容量一般指在一定空域结构下考虑管制规则和一些相关因素(如军事活动)的影响，且一直有航空器在终端区进出的情况下，单位时间内所能容纳的最大航空器数量。

1.3 最大流最小割定理

在任一个网络G的所有割集中，其最小的割集流量之和就等于该网络最大流的流量。

目前，已经有人将最大流最小割理论应用在多边形中，用两条边来代表源(S)和汇(T)。而在从源(S)到汇(T)的各个通路中，其通行能力由容量来决定。而整个网络中容量最小的部分就是网络的最小割，也就是整个网络的咽喉部分或者瓶颈，是决定该网络通行能力的直接因素。多边形最小割示意图如图1所示。

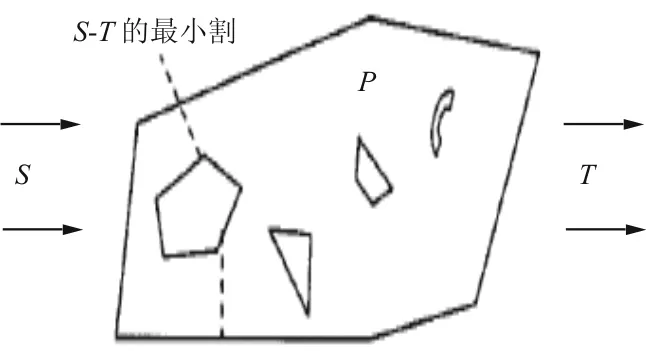
图1 多边形最小割示意图

2 飞行受限区的划设

2.1 飞行活动区的确定

军用航空飞行活动往往会受到飞行员动作误差、空中风向的影响，不同的动作所需要的空域范围是不同的。在确定飞行受限区时，需要确定不同科目所需要的活动范围。本文中军用航空飞机所需要的空域范围是利用数学模型，并结合飞行特点来确定的，通过蒙特卡洛法确定实际的圆心和机动半径，进而求出右侧边界的位置。

2.1.1 转弯半径的计算

通常战斗机飞行员的动作误差服从正态分布，其分布函数为

(1)

式中：Mshould为期望动作误差；Mlast为实际动作误差；σp为标准差。

在飞机飞行训练的过程中，影响飞机机动轨迹的因素主要有机动起点、转弯的坡度、转弯的速度、风及其导航设施的精度等，飞行轨迹图如图2所示，其中飞机的期望机动轨迹为实线所示，然而由于受到了全向风和动作的影响，其运动轨迹如虚线所示。

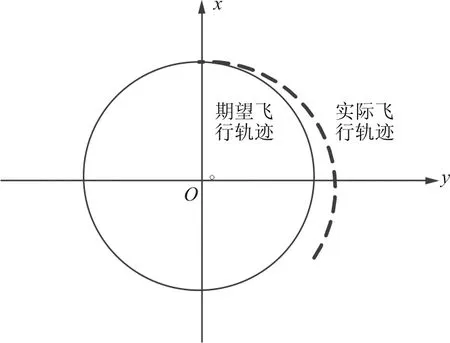
图2 飞行轨迹图

通过转弯半径的计算可知转弯半径与其飞行速度及坡度的关系为

(2)

假设期望的飞行速度v=250 m/s(900 km/h)，期望转弯坡度γ=45°，由于受到动作误差的影响，其服从式(1)的正态分布，因此在速度误差和转弯坡度误差影响下的转弯半径为

(3)

其中实际速度和实际转弯坡度服从正态分布：

(4)

2.1.2 转弯轨迹圆心计算

将实际圆心位置定义为O1(x1,y1)，期望的圆心坐标为O(xs,ys)，且在机动过程中只考虑转弯过程中的影响，则实际圆心坐标为

(5)

式中：θ为飞机开始盘旋时的航向角。

2.1.3 空域半径的计算

空中飞行的航空器不可避免地会受到风的影响，然而在进行航迹估计的过程中是无法确定风向的。因此，国际民航组织在航路划设的过程中定义了一个对航空器最不利的风向——全向风，全向风为转弯时垂直于飞机当前航向向外的风向。假设全向风的风速为w，则在全向风的影响下，实时转弯半径可以表示为

(6)

式中：a为飞机转过的角度数。

因而最终所需的空域范围半径A为

A=x1+R1

(7)

2.2 飞行受限区的划设

航空器在实际飞行中，往往需要进行多种科目的练习。为保证飞行安全，军方飞行活动空域及其保护区内均无法通过民用航班，本文将此区域定义为飞行受限区，通常用二维区域来表示。

划设飞行受限区主要是利用最小外接矩形法。利用面积较小的矩形不断逼近军方活动的空域，当矩形的边与军方活动空域相切时，形成的矩形为受军事活动影响的空域(如图3所示)。此方法首先需要确定军方活动空域在坐标轴上的极值，即在x轴上的最大值xmax与最小值xmin，以及y轴上的最大值ymax与最小值ymin。四个点形成的区域为初始面积较小的空域：(xmin,ymin),(xmin,ymax)，(xmax,ymin),(xmax,ymax)。将初始扫描线的角度设置为0，之后按照一定的增量dA增加，扫描线为两组相互垂直的边。将扫描线沿着目标矩形的边界移动至与活动空域相切为止。此时形成的矩形为该扫描角度下的外接矩形。根据相关法规,军方活动空域离航路航线需要保持10 km的水平间隔,因此将各扫描角度下面积最小的外接矩形增加安全间隔后定义为受军方飞行活动影响的空域，即飞行受限区(如图3阴影区所示)。

图3 起始外接矩形及其扫描示意图

利用外接矩形划设飞行受限区的流程图，如图4所示。

图4 飞行受限区划设流程图

3 终端区容量评估方法

军事活动作为影响空域容量的因素之一，通过构建终端区容量评估模型，利用最大流最小割原理可以找出受军事活动影响下的空域容量瓶颈，并利用改进的遗传算法来对模型进行求解，以确定影响下的空域容量。

3.1 模型构建

3.1.1 假定条件

本文将终端区看作是一个网络，其中的飞行受限区看作网络中的多边形区域(不能流过的区域)，则利用最大流最小割理论就可以求取该终端区内的动态容量。在此模型中，假定：

(1) 航空器进离场均使用同一条跑道；

(2) 进离场航线中，每条航段的距离均已给定；

(3) 航空器在任一条航段上均以平均速度飞行；

(4) 在每条航段上只能单向飞行，且飞行方向已经给定；

(5) 对流天气的影响区域为中间航段；

(6) 在终端区没有等待区，所有航空器均是即到即走。

在这些假设成立前提下，终端区的容量就是指在单位时间内经过终端区入口点的最大航班量。

3.1.2 弧容量求解

为了计算终端区的动态容量，需要计算每段弧上所能容纳航班的最大数，即该航段的容量。具体公式为

(8)

(9)

(10)

(11)

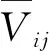
换算因子Kij为

(12)

对于换算因子Kij的计算，本文可根据高度和温度求出，也可以通过查询换算因数表就可以得知；如果给定的高度或者温度没有列出，可用内插法求其值。利用以上公式，就可以计算得出航段的容量，即网络图中的弧容量Cij(t)。

3.1.3 评估模型构建

在计算出终端区网络示意图中每条弧的弧容量后，将划设的飞行受限区标记在网络图中，并以此构建在天气影响下的终端区容量的动态评估模型。

将所需要的变量用以下符号表示：Bij(t)为t时刻下，航段Aij上的航班数；Iij(t)为(t,t+1)时段内，流入该航段Aij的航班数；Oij(t)为(t,t+1)时段内，流出该航段Aij的航班数；fij(t)为(t,t+1)时段内，该航段Aij净流出量，即流量。Iij(t),Oij(t),fij(t)三者之间的关系为

fij(t)=Oij(t)-Iij(t)

(13)

本文用S表示该网络的源，用T表示该网络的汇，那么航段Aij在时段(t，t+1)内的净输出量为

(14)

而此规划模型中的约束条件如下：

(1) 航段Aij上的容量约束：0≤fij(t) ≤Cij(t)；

(2) 非负整数约束:Bij(t)≥0，fij(t)≥0。

在军方活动过程中，航班不得经过划定的飞行受限区。为了在该模型中将军方活动的影响纳入其中，假定如果某航段在飞行受限区内，那么该航段暂时不允许航空器通过。本文将军事活动作为一个变量因子ζij(t)。

当ζij(t)=0时，说明该航段受到了军事活动影响；

当ζij(t)=1时，说明该航段不受军事活动影响。

本文将计算得到的网络最大流maxv(f)对时间t进行求导得到最终的进场容量：

(15)

在计算出终端区的进场容量之后，还需要求出终端区的离场容量Cdep。同理，将跑道的离场端作为起点，终端区的出口点作为终点建立终端区离场网络示意图，之后参考进场容量的计算方法就可以得到离场容量Cdep。

通过式(15)，就可以计算出该终端区的动态容量C：

C=Capp+Cdep

(16)

3.2 模型求解方法

求出终端区容量的关键是确定该网络的最大流。根据最大流最小割定理，可以利用改进的遗传算法进行求解。

3.2.1 传统算法的分析比较

求解网络最大流最小割问题其实是一类组合优化问题。目前比较常见的方法有Ford-Fulkerson标号算法[11]、预流推进类算法[12]等。Ford-Fulkerson是利用标号的方式来找寻增广链路。通过不断增加增值链上的流量到无增广链为止。其算法的复杂度为O(nm2)，由于受算法的限制，此算法不适用于大规模的编程。而预流推进算法则是在标号法的基础上提出的改进算法，其复杂度为O(n2m)。可以看出，传统方法随着节点数目的增加，计算的复杂度会呈指数上升。为避免该问题，本文根据最大流最小割定理，结合遗传原理，设计了求解最大流最小割问题的遗传算法。

3.2.2 改进遗传算法的设计求解

3.2.2.1 编码与解码方式

初始群体：随机生成N个可行解作为初始群体。对于每个个体，进入点必须为1，终点必须为0，其余点为随机生成的二进制代码0或者1。

3.2.2.2 适应度函数

由于在求解终端区动态容量的过程中，需要找出网络是最小割集容量。因此，将每个割集的容量作为适应度，即：

(17)

3.2.2.3 选择算子

在群体中，每个个体都按照一定的概率进行交叉与变异，个体越接近最优解越容易被选择。在动态容量求解的过程中，适应度值越小，越接近最优解。而遗传算法求解中则是适应度值越大越容易被选择，因此，在计算适应度以后需要对其进行归一化处理。

将群体中适应度的最大值记为cmax，最小值为cmin。为结合实际情况，将个体的适应度函数更改为

(18)

3.2.2.4 交叉算子

(19)

如：(101001)⊗(110001)=(111001)。

3.2.2.5 变异操作

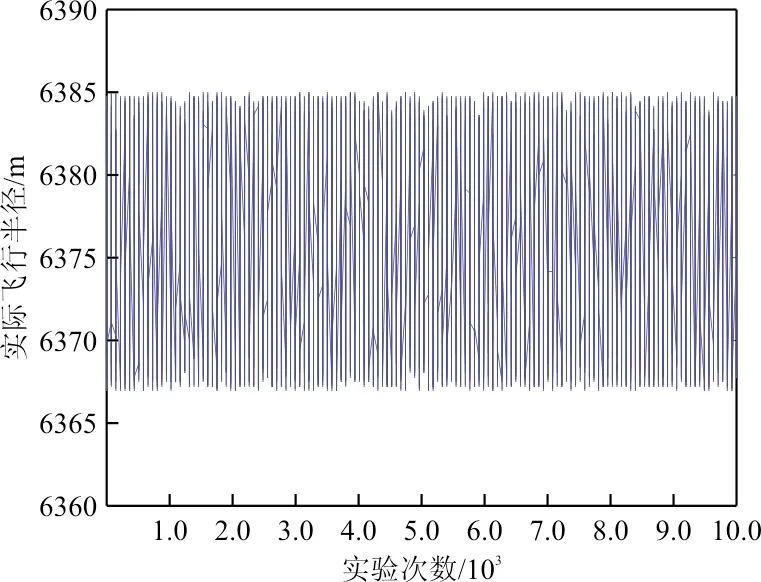
假定变异概率为Pm，对于每个新个体中的顶点(非进入点或者终点)，随机生成一个0～1之间的数字r，若r

3.2.2.6 算法步骤

Step1: 初始化种群，随机生成N个可行解。

Step2: 分别计算每个可行解的适应度值，并作归一化处理，选择其中适应度值最佳的个体遗传到下一代个体中。

Step3: 选择相应的父本和母本，根据概率Pc的大小进行交叉操作，产生对应的个体。

Step4: 对产生的新个体进行变异操作，并作为下一代种群。

Step5: 重复Step3～Step4,直至下一代种群个体为N。

4 算例仿真

本文以某机场终端区为例，计算该机场某一时段的离场容量。假设军方当天的训练科目为盘旋机动和8字机动。采用蒙特卡罗法选取符合速度、坡度的概率密度函数分布的随机数，进行n=1 000 000次的军用航空飞行仿真，仿真计算的参数如表1所示。最终位置偏差结果如图5～图6所示，为方便显示截取了前10 000次的仿真数据。

表1 仿真相关参数

图5 实际圆心横坐标位置图

图6 实际半径图

通过实例仿真发现，军用航空飞机在作盘旋机动时，圆心最大的偏离距离在横坐标上的投影为4.732 m，实际飞行过程中半径最大为6 384.36 m，因此当飞行在作盘旋机动时，可以将其活动范围划定为半径为7 km的圆形区域。

对于8字机动，本文假设飞机在做完转弯机动后，平飞时间为8 min，在考虑全向风的情况下，通过对其动作的1 000 000次仿真，寻求其右边界距离坐标原点的最大距离，结合飞行半径的变化情况确定最终的空域范围。通过对1 000 000次的数据分析，其边界最远距离为15.832 km，最大半径为6.432 km，因此空域范围为13 km×23 km的距形区域。飞行动作示意图如图7所示，前10 000次最右侧的边界偏差示意图如图8所示。

图7 动作示意图

图8 右侧边界距离图

利用最小外接距形法，将军事活动的影响区域标记为飞行受限区，并将其影响范围标记在离场图上，该机场的离场的结束点为N1、N2、N3、N4;离场的开始点为N19；其余航路点均作为中间节点，建立受军事活动影响的离场网络示意图，如图9所示。

图9 军事活动影响下的网络图

假设该终端区上的机型比例大致为：重型机22.89%(其进近速度280 km/h);中型机76.89%(其进近速度为250 km/h)；轻型机0.22%(其进近速度为215 km/h)。

根据示意图本文可看到航段集合为

A={A197，A711，A1110，A109，A98，A93，A83，A1918，A1814，A1413，A1312，A128，A181，A1817，A1716，A1715，A154，A144，A76，A65，A52}

而各航段的长度(km)依次为

L={13，54，24，10，22，17，15，11，14，28，23，39，64，20，31，7，47，68，19，38，62}

相应的限制飞行高度(km)为

H={1.3，1.5，1.2，1.2，0.9，0.8，1.1，1.3，0.7，2.7，1.7，1.4，1.5，1.8，1.6，1.2，4.5，3.5，1.3，1.7，2.1}

根据温度以及各航段的高度查询换算因数表或利用内插法计算，本文可以得到速度的换算因子

K={1.087 6，1.104 6，1.072 3，1.081 6，1.041 7，1.032 6，1.051 2，1.032 9，1.103 6，0.987 6，1.172 4，1.083 2，1.095 2，1.114 6，1.091 2，1.071 6，1.291 7，1.224 5，1.071 8，1.097 2，1.132 5}

将上述各参数代入式(8)～式(12)中，求出每个航段的静态容量。之后，利用改进的遗传算法来求解网络的最大流最小割容量。假定初始种群个体数为N=10，迭代代数为40，进行100次重复试验，实验结果如图10所示。

图10 实验结果图

利用改进遗传算法可以求得在有军事活动影响的情况下，该网络的最大流最小割容量Cdep=14.5架次。利用文献[12]中的最大流最小割算法对问题进行求解，得出的结果仍为Cdep=14.5架次。从图10可以看出：在100次实验中仅有2次实验结果出现误差，其他情况下均能够得出正确结论。

而利用改进遗传算法与传统算法在运行时间上的对比情况如图11所示。

图11 运行时间对比图

从图11可以看出：相较于传统最大流最小割算法，利用改进的遗传算法不仅能较为准确地预测终端区容量，而且所需要的计算时间少于传统算法，效率更高。利用传统的数学分析法，主要利用固定方法求解数值，算法的复杂度会随着节点的增多呈指数型增加；改进算法主要利用智能算法搜索寻优的能力，算法的运算效率主要和种群规模有关，而与节点数量关系不大，因此利用改进的遗传算法求解终端区容量可以有效避免由于节点增多而引起的复杂度增长的局限性。终端区容量会由于军事活动的影响而变化，及时地计算出终端区动态容量能够使终端区运行更加高效合理。