基于截面视角的一类问题情境创设

昆明市西山区第一中学 云南省高中数学于雷名师工作坊 陈国勇

《普通高中数学课程标准（2017年版）》指出：基于数学学科核心素养的数学活动，应该把握数学的本质，创设合适的教学情境，提出合适的数学问题，引发学生思考与交流，形成和发展数学学科核心素养.创设合适的情境，提出合适的问题，是落实核心素养的关键.在时下的课堂教学中，教师们有时煞费苦心地创设情境，却难以打开学生的心扉.诚然，“如何创设问题情境”已成为一线教师设计教学时首要思考的问题.下面，笔者以“用截面创设问题情境”为话题，谈谈自己的一点肤浅认识，以便与各位同仁交流.

一、用截面创设圆锥曲线绪言课的情境

圆锥曲线是高中教学的重要内容，蕴含着逻辑推理、直观想象、数学运算等核心素养.王尚志教授曾指出要重视圆锥曲线绪言课的教学.他在北京某中学调研时问高三学生：“圆、椭圆、双曲线、抛物线都称为圆锥曲线，它们和圆锥有什么关系呢？”当时学生并没有给出准确的答案.落实核心素养要整体把握教学内容.作为每一章节起始部分的绪言，是整体把握该章内容、建立知识内在联系的重要内容.在圆锥曲线一章的绪言课中，教师应顺应圆锥曲线的起源背景，用平面去截圆锥进行情境创设.

案例1：圆锥曲线的起源.

情境与问题：如图1，用一个平面去截圆锥，截口曲线（截面与圆锥侧面的交线）会出现哪些形状？

创设意图：通过多媒体信息技术制作课件，调整平面的倾斜角度，使其截面出现圆、椭圆、双曲线、抛物线，让学生动态感知、整体把握圆锥曲线的生成过程，激发学生的学习兴趣，顺利开启本章知识的学习.

图1

二、用截面创设立体几何发现定理的情境

定理课是立体几何教学的重要课型，其教学内容是某个定理，通常蕴含着逻辑推理、直观想象等核心素养.在教学中落实核心素养，关键在于把学生带入定理的探究学习活动中.因此，创设情境，引导学生自然地去发现定理，是启发学生思维的关键.

案例2：线面平行的性质定理.

情境与问题：如图2，已知直线a 与平面α，且a∥α，用过a 的平面β 去截平面α，你有什么发现？

图2

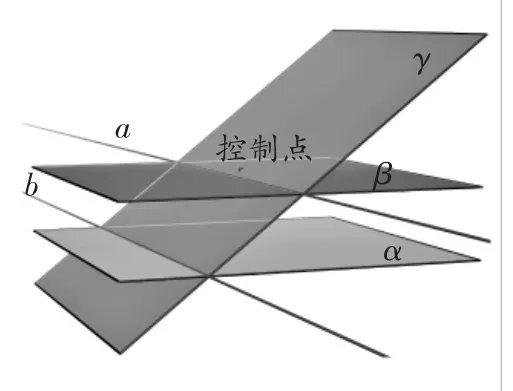
图3

案例3：面面平行的性质定理.

情境与问题：如图3，已知平面α 与平面β，且α∥β，用一个平面γ 同时截平面α 与平面β，你有什么发现？

案例4：面面垂直的判定定理.

情境与问题：如图4，已知直线a 与平面α，且a⊥α，用过a 的平面β 去截平面α，你有什么发现？

创设意图：高中阶段立体几何教学的一个重要任务是教学生学会逻辑思考.教材中对这几个定理的教学，是在引导学生观察现实生活中一些物体位置关系的基础上进行的，无论是观察长方体模型，或是直接以例题的方式给出，都不能让学生很好地从点、线、面的位置关系去发现定理.因此，引入平面，从截面视角引导学生发现结论，过程自然流畅，更能揭示知识的本质.

图4

三、用截面创设探究某一几何体性质的问题情境

立体几何的教学离不开研究几何体的性质，使得设置合适的问题情境，引导学生进行深度思考、积极参与数学探究活动、积累数学活动经验，是发展学生核心素养的有力抓手.然而，在设计教学时，教师常苦于缺乏自然的视角来创设合适的情境，以致枉费心机，到最后落得学生思维得不到启发、教师只能自圆其说的尴尬境地.此时，教师若能从截面的视角创设情境，不仅能使问题一般化，而且能打开学生思维的匣子.

案例5：正方体截面的探究.

图5

情境与问题：如图5，用一个平面截正方体，截面的形状将会是什么样的？

1.给出分类的原则（如按截面图形的边数分类），按照你的分类原则能得到多少类不同的截面？设计一种方案，找到截得这些形状的截面的方法，并在正方体中画出示意图.

2.如果截面是三角形，你认为可以截出几类不同的三角形（分别按边、角进行分类）？为什么？

3.如果截面是四边形，你认为可以截出几类不同的四边形？为什么？

4.还能截出哪些多边形？为什么？

5.能否截出正五边形？为什么？

6.能否截出直角三角形？为什么？

7.有没有边数超过6 的多边形截面？为什么？

8.是否存在正六边形的截面？为什么？

9.面积最大的三角形截面是哪个？为什么？

10.你自己发现的相关问题还有哪些？

创设意图：用一个平面截正方体，截面的形状将会是什么样的？启发学生提出逐渐深入的系列问题，引导学生完成探究、发现、证明新问题的过程，积累数学探究的经验.

四、用截面创设立体几何考试题的情境

作为承载逻辑推理及直观想象核心素养的立体几何，是高考考查的主干知识之一，近几年所占的分值在22分左右.如何创设背景公平、体现立体几何本质的试题情境，一直是命题者努力创新的方向.

案例6：（2018年全国Ⅰ卷理科第12题）已知正方体的棱长为1，每条棱所在的直线与平面α 所成的角都相等，则α 截此正方体所得截面面积的最大值为（ ）.

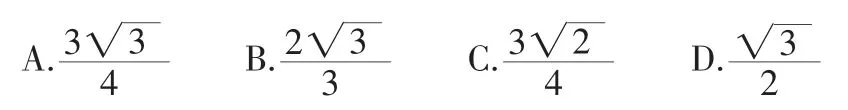
案例7：（2015年全国Ⅱ卷文理第6题）一个正方体被一个平面截去一部分后，剩余部分的三视图如图6 所示，则截去部分与剩余部分体积的比值是（ ）.

图6

创设意图：以平面截正方体为情境进行设问，重点考查立体几何中点、线、面的位置关系，突出考查考生的空间想象能力、运算求解能力和逻辑推理能力，体现的核心素养是直观想象、逻辑推理、数学运算.

五、用截面创设立体几何复习课的情境

在对立体几何进行复习时，教师苦于资料多、时间紧、讲得多、教得累，学生厌于知识碎、难掌握、作业多、时间少、学得苦，教与学都落入效果差的不良境地.此时，教师若能找准合适的角度创设情境，有效地整合例题、习题、真题，提出本质的问题进行变式追问，启发学生运用所学立体几何知识及研究问题的一般方法进行深度思考，发现问题、提出问题、分析问题、解决问题，让学生有所体验、有所收获，就能提高复习的效果，改变不良现状.

案例8：立体几何复习.

我们先来看一下最近的考题：

1.（昆明市2020届高三“三诊一模”测试理科第10题）某同学在参加《通用技术》实践课时制作了一个工艺品，如图7 所示.该工艺品可以看成是一个球被一个棱长为的正方体的六个面截后剩余的部分（球心与正方体的中心重合）.若其中一个截面圆的周长为4π，则该球的半径是（ ）.

图7

2.（2020届四省名校高三第二次大联考第12题）在棱长为2 的正方体ABCD-A1B1C1D1中，E，F 分别为A1D1，D1C1的中点，则过B，E，F 三点的平面，截该正方体所得截面的周长为（ ）.

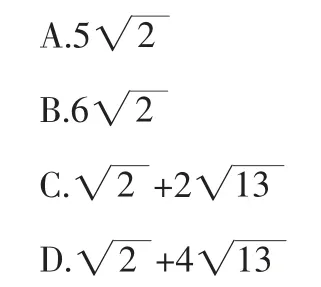
图8

再看书上的例题：

3.（人教A版数学必修2第28页习题1.3A组第3题）如图8，将一个长方体沿相邻三个面的对角线截出一个棱锥，求棱锥的体积与剩下几何体的体积的比.

既然从“截面”视角命题是立体几何的热点，我们可以考虑从“平面截几何体”的视角创设如下情境与问题，提高复习的效率.

情境1：用一个平面截棱长为a 的正方体.

问题：

1.截面的形状有哪些？

2.你能画出示意图吗？

3.这些截面中存在面积最大的截面吗？若存在，最大截面的形状是什么？面积是多少？周长是多少？

4.若截面把正方体分成体积相等的两部分，这样的截法有几种？你能画出示意图吗？

情境2：用平面（可用多个平面）截棱长为a 的正方体.

问题：

1.你能截出正四面体吗？（画出示意图）

2.你能截出几种不同的三棱锥？（画出示意图）

3.你能试着计算你截出的几何体的表面积和体积吗？

再次创设情境，进行变式追问，引导并鼓励学生类比以上情境提出如下问题.

情境3：如图9，若用一个平面分别截圆锥、圆柱、正四面体或直三棱柱，你能提出那些问题？你能尝试解决自己提出的问题吗？

图9

创设意图：深入研究课本中的习题与考题，从截面的视角创设情境，并进行有效整合、变式追问，引导学生发现问题、提出问题、分析问题、解决问题，巩固立体几何基础知识，提升作图、用图、直观想象等能力.

从截面视角创设情境、提出问题，相当于用点、线、面、体中平面这一要素作为参照，去类比发现问题、提出问题、分析问题、解决问题，能较好地揭示立体几何的本质，让学生动手操作、直观感知，符合学生认识事物的基本规律，实为立体几何中创设问题情境的一种有效方法，可以切实地提高教学的效率.