类比推理法在大学数学教学中的应用

刘懿辉

(延安大学西安创新学院 计算机学院，陕西 西安 710100)

0 引言

高等数学是大学数学的基础课程，属于工科类专业的必修课程，作为大学生学习其他专业知识的重要工具，教师在讲解其相关概念、理论、定理等过程使用类比推理方法(下文简称“类推法”)，能够启发学生思维，对其创新能力的提升具有重要意义.

1 类比推理法概念和模式

1.1 概念

类推法主要是找出两个对象存在的相似、相同等属性，进而展开类比，推断出在其他属性方面也存在类似之处的系列推理过程.这种方法对个别现象展开观察，与归纳推理方法相似.但同时此方法属于由特殊向特殊方向的推理，因此，与归纳推理由特殊向一般的过程不同.类推法分为完全类推和不完全类推两种形式.其中，完全类推指的是对两种事物展开相同对比，不完全类推是对两种事物展开不完全相同的比较.在大学数学教学中，使用此方法能够使学生更好地发现、解决问题，通过向学生传授学习方法，逐渐培养学生思维，提高其解题能力.

1.2 模式

2 在大学数学中应用类比推理法的意义

高等数学具备严谨的理论系统，教材中主要以概念讲解、性质介绍、公式呈现和定理证明等内容为主.教学环节，教师需要重点通过推理方式为学生传授知识，进而培养大学生的逻辑思维.使用类推法可从数学历史发展的角度，对各种数学问题展开观察和类比，通过总结，找出问题解决途径.因此，应用类推法进行教学(以下把这种方法称为类推教学法)能够结合实际学情，从学生兴趣入手，重点培养大学生的学习、钻研和创新等能力，此方法的应用具有如下三点意义：首先，讲授高等数学知识时，使用类推教学法，能够结合实际问题，创设情境，引导大学生发现问题，并提出新的可能性或者问题，利用自身已掌握的知识，以全新的视角发现事物独有的同类特点，在复习以往知识的基础上，学习新的知识；其次，使用类推教学法，能够引导学生对问题的本质展开探究，从多个维度对问题展开分析.高等数学当中涉及多个概念、多种公式，利用此方法学生可更好地学习抽象概念，展开创新，对完善大学生的数学思维有重要作用；最后，使用类推教学法，可清晰地向学生呈现出数学知识之间的逻辑关系以及形成过程，引导学生联系知识本质，展开创新，学习更多解决问题的方法.

3 大学数学教学中类比推理法的应用

3.1 概念类比

3.1.1 积分概念

在数学领域中，概念主要指的是研究对象本质的抽象表达，即通过概念讲解将对象本质揭示出来.类推法作为启发性的教学方法，能够更好地揭示积分相关概念.高等数学中积分概念共分为7个种类，分别为定积分、二重积分、三重积分、第一类曲线积分、第二类曲线积分、第一类曲面积分、第二类曲面积分，每一个积分概念对应一类概念，并且相互之间存在紧密联系.上述积分概念组成大致相同，在讲解以上概念的过程中常利用几何知识，结合物理意义进行讲解.首先引入例题，分析问题、研究解题思路，利用分割思想、近似求和，最终取极限值进行定义，从而揭示积分概念内涵.因此，可利用定积分的概念，展开类比，讲解其他种类的积分概念，启发学生自主总结其他积分概念.学生通过已知的概念，可掌握积分相关概念本质，进而更好地学习其他概念.

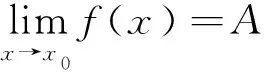
此外，高等数学的常微分方程中，方程通解存在相似性质.例如根据一阶线性非齐次方程通解等于其对应的齐次微分方程通解和该非齐次微分方程特解之和，使用类推法展开推理，可获得如下结论，即二阶线性的非齐次方程，其通解等于对应齐次微分方程通解和该非齐次微分方程特解之和.

3.1.2 指数函数

3.2 定理类比

3.2.1 微积分定理

3.2.2 广义积分

3.3 空间平面类比

数学家Geore Polya曾经说过，“类比在数学学习过程是个领路人，能够根据平面几何知识解决立体几何相关问题”，即通过相似的条件推导出类似结论，这一观点在平面和空间二者的类比中应用明显.

3.4 无限的类比

部分数学问题难以通过有限次运算进行精确求解，此时需要找出无限变化趋势，通过规律将问题求解出来，高等数学中微积分就是利用此思想建立的.大学生已经掌握部分初等数学的求解方式，可以解决部分有限问题，对于分析、求解无限问题时，即可使用类推思维.在高等数学教学过程中，从有限向无限过渡，单纯使用类比推导方法可能获取的结果并不精准，对此可结合实际情况对结果展开适当的修正，进而获得正确的结论.

4 结语

总之，在高等数学教学中，通过类推法能够指导学生不断深入地思考、系统地归纳数学知识，同时将不同层次知识串联起来，强化记忆效果.通过数学教学过程概念和定理的类推，启迪学生触类旁通，举一反三，提高了学生的思维能力，教学成效明显.