基于有源功率因数校正的直流充电桩控制策略研究
2020-06-24钞凡何志琴胡秀敏李志远刘莉
钞凡 何志琴 胡秀敏 李志远 刘莉
(贵州大学,贵阳 550025)
主题词:三相电压型脉冲宽度调制整流器 空间矢量脉宽调制双环控制 有源功率因数校正技术 谐波污染 电能质量
1 前言
电动汽车充电桩是影响电动汽车产业快速发展的重要因素[1],目前,仍存在着许多制约其发展的技术瓶颈,如电能质量问题[2]。直流充电桩的结构对其电能质量有很大影响[3],合理的充电桩结构能够实现安全、高效、高功率因数、低谐波的优质电能输出[4]。传统整流装置的功率因数通常为0.45~0.75,而功率因数越低的整流装置产生的谐波越多,所以传统整流器,特别是传统大功率整流器产生的谐波对电网的污染和危害巨大,也严重影响电能质量。文献[2]考虑车载式充电器的谐波对电网的影响,将有源电力滤波技术应用于充电桩设计,有效提高了电网侧电能质量,但增加了额外的滤波装置导致控制策略运算复杂,文献[3]采用增大电感的方法降低了谐波含量,但同时也导致了充电桩的体积增大,增加了成本。
本文针对直流充电桩自身结构对电能质量的影响,将有源功率因数校正(Active Power Factor Correction,APFC)技术引入直流充电桩整流主电路,采用空间矢量脉宽调制(Space Vector Pulse Width Modulation,SVPWM)算法的双闭环直接电流控制提高电能质量,并通过仿真验证该方案的有效性。
2 三相电压型脉冲宽度调制整流器数学模型
三相电压型脉冲宽度调制(Pulse Width Modulation,PWM)整流器在三相静止坐标系下的数学模型为:
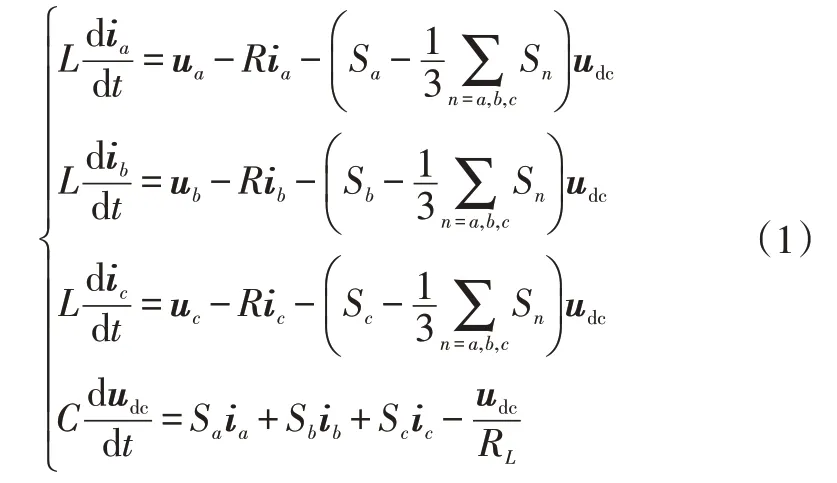
式中,ua、ub、uc为电网三相电压;R为滤波电感的等效电阻;udc为直流母线电压;C为直流滤波电容;Sn(n=a,b,c)为桥臂的开关状态,Sn=1表示开,Sn=0表示关;RL为负载电阻;L为网侧电感;ia、ib、ic为网侧电流。
式(1)简化后可得同步旋转坐标系下的数学模型为:

式中,ω为dq坐标系的旋转角频率;idc为直流母线电流;id、iq分别为电流矢量在d、q轴的分量;ud、uq分别为电网电压矢量在d、q轴的分量;Sd=ud/udc;Sq=uq/udc。
由式(2)可以看出,电流的d、q分量相互耦合,不利于控制器的设计,必须进行电流的解耦。鉴于此,可以将交流控制变为直流控制,简化控制思路。
3 直流充电桩APFC控制策略研究
SVPWM是基于dq坐标系变换的矢量控制,通过控制PWM 整流器的有功电流和无功电流,达到控制输入侧电流的目的[5-6]。相比于其他控制策略,SVPWM 成功地将时变量的交流量转换为直流量,实现控制系统设计的简化。该控制策略主要采用abc三相静止坐标转dq两相旋转坐标的坐标变换思路和SVPWM调制算法,来实现电能质量的优化和控制器的简化。
结合式(1),有:

式中,uao、ubo、uco为整流器交流侧相电压基波电压的瞬时值。
在整流电路中,6 个功率开关器件采用上、下开关管换流工作方式,故开关管共有23=8 种开关状态,将8种开关状态代入式(3),即得到相应的三相电压型PWM整流器网侧电压,这8个矢量由2个零矢量u0、u7和6个非零矢量u1~u6组成,且无论开关组合怎样变化,交流侧电压矢量都可以用模为2|udc|/3 的电压矢量来表示。故定义三相PWM整流器交流侧电压空间矢量un为[7]:

将式(3)代入式(4),可得:
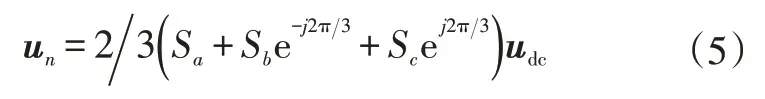
由式(5)可以得到8个基本矢量的幅值及其在矢量平面内的相位,其6 种有效的工作状态依次切换,并在π/3的时间内保持不变。根据固定相位的关系,可得电压空间矢量分布及合成情况如图1所示。

图1 电压空间矢量分布及合成
由图1可知,此时的系统被分成6个扇区,任一扇区中的电压矢量ug都可以用u0~u7合成,使合成矢量不断逼近给定的参考指令电压空间矢量,从而达到SVPWM控制的目的。
4 直流充电桩APFC电路参数设计
4.1 交流侧电感的设计
4.1.1 满足快速电流跟踪指标时的电感取值
首先,当三相电压型PWM 整流器运行在单位功率因数正弦波电流控制时,分析满足快速电流跟踪要求时的电感值[8]。
令A相电压为:

再忽略其系统网侧交流等效电阻r,同时将式(6)代入式(1),可得:
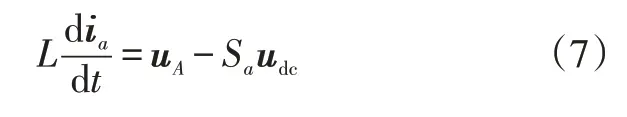
为使实际电流实时追踪指令电流,必须满足电流快速跟踪指标对开关管开关周期的要求,这里以电流过零的瞬态过程进行分析。
图2所示为电流过零处开关周期电流跟踪波形,由图2可知,稳态条件下,在T1时间段内,A相下桥臂导通,电感存储能量,电流上升,Sa=0,故可得:

式中,Δi1为A相下桥臂导通时的电流变化量。

图2 电流过零处开关周期电流跟踪波形
而在T2时间段内,A 相上桥臂导通,电感向负载充电,电流下降,Sa=1,此时式(7)可改写为:

式中,Δi2为A相上臂导通时的电流变化量。
又因为要满足电流的快速跟踪要求,则实际电流在开关周期内的上升速度必须快于指令电流的上升速度。因此有:

式中,Ts为开关周期;Im=|im|,im为电流最大值。
联立式(8)~式(10),再结合电流变化率最大化情况(T1=Ts),可得:
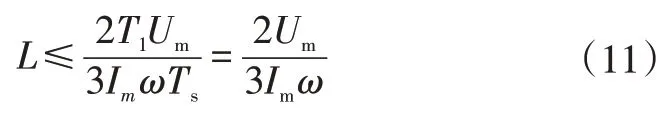
式(11)即为满足快速电流跟踪指标时的交流侧电感取值。
4.1.2 满足交流侧电流谐波抑制时的电感取值
图3 所示为峰值条件下电流跟踪瞬态过程,由图3可知,稳态条件下,在T1时间段内,Sa=0,又由Ts很小,故有ua=um,ia=im,其中um为电压最大值,且|um|=Um,得:
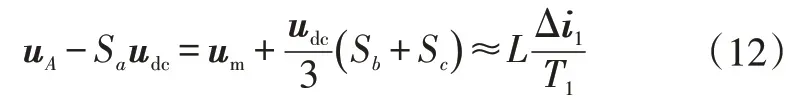
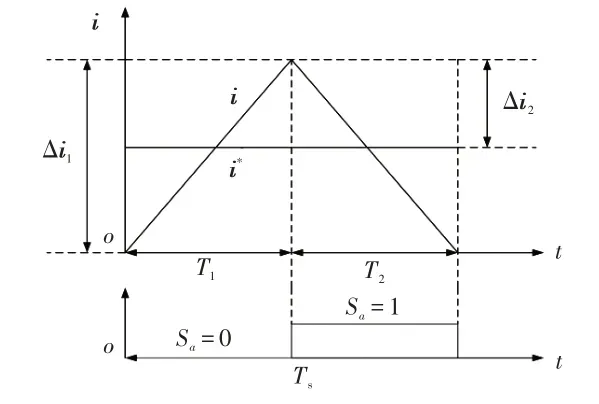
图3 电流峰值时电流跟踪瞬态过程
而在T2时间段内,A 相上桥臂导通,Sa=1,此时式(8)可改写为:

由图3可知,考虑到电流峰值附近1个开关周期中,有Δi1+Δi2=0,再令Sb=Sc=0,可得:

式中,Udc为udc的幅值;Δimax为最大允许谐波电流脉动量,一般取Δimax=0.2Im。
综上,由满足快速电流跟踪指标和满足交流侧电流谐波抑制的两种广泛情况,最终确定交流侧输入电感的取值范围为:
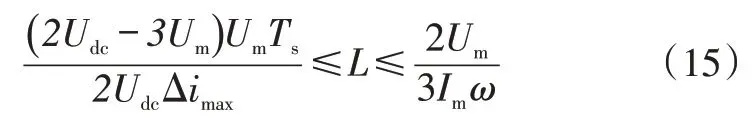
再由系统给定参数,最终求得所取电感的取值范围为0.27 mH≤L≤13.8 mH。在系统仿真和试验测试时,交流电感的最终取值视具体情况而定。
4.2 直流侧电容的设计
对于直流充电桩功率因数校正模块,其主电路元件参数设计中除交流侧电感外,直流侧电容的选取也十分重要。
4.2.1 满足电压环控制的抗扰性指标
如前文所述,从系统鲁棒性和满足直流侧电压抗扰性[9-10]等方面分析,选用的主电路拓扑结构为第2 章所述的三相电压型PWM整流器,故直流侧电容应满足:

式中,Umax为三相电压型PWM整流器负载端电流出现阶跃扰动时的直流电压最大压降。
4.2.2 满足电压环控制的跟随性指标
电压快速跟踪控制性能[11-12]本质上是通过快速控制直流侧电压加快电压外环的响应速度,故直流电容应满足:

结合式(17)可得:

根据系统给定值,结合上述两个方面的理论与分析,可得直流侧电容的选取范围为0.001 F≤C≤0.25 F。在系统仿真和试验测试时,直流电容最终取值视具体情况而定。通过上述分析计算,主电路参数的选取更具目标性。
4.3 PI控制器参数设计
4.3.1 电流控制环参数设计
在旋转坐标下,由于电感的存在,d轴和q轴间的电流相互耦合、相互影响,所以采用前馈解耦控制,且采用PI调节器进行调节,从而实现d轴和q轴的独立控制,提高系统的动态性能。
在三相电网平衡条件下,根据三相同步旋转坐标下的电压指令公式,有:

式中,ed、eq为三相VSR 电压矢量的d、q轴分量;Kip与Kil分别为PI调节器的比例系数与积分系数,分别为d、q轴电流分量的参考值。
为消除ωLid、ωLiq、ed和eq的影响,简化设计,结合式(2),式(19)可改写为:
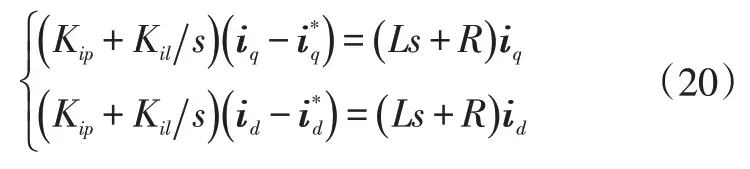
由式(20)可知,d、q分量已完全独立,只需确定Kip与Kil,而实际分析中,通常还需考虑电流采样的延时和整流器本身的时间常数影响等,故内环结构如图4所示。

图4 电流环结构
其中Tic、Tds和Kpwm分别表示电流环采样时间、整流器的延时时间和桥路PWM 等效增益。取Tic=0.1Ts和Tds=0.5Ts,令Sq=0,Kil/Kip=R/L代入其闭环传递函数,故可得:

根据二阶系统的特征,在阻尼比ξ=0.707 时,系统的超调量和调节时间较为合适,进而推导出调节器的比例系数,并根据式(21)得到积分系数:
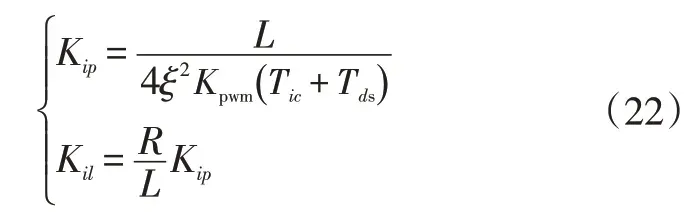
由以上分析可知,只要系统的开关频率足够高,电流内环便可得到快速的动态响应。本文选取IGBT功率开关管的开关频率为20 kHz,所以响应速度已得到满足。
4.3.2 电压控制环参数设计
在三相压敏电阻器(Voltage-Sensitive Resistor,VSR)中,开关管的开断频率远大于网侧电动势基波频率,故可以忽略PWM谐波分量,只考虑开关函数的低频分量。因此开关函数的表达式为:

式中,m为PWM调制比;θ为开关函数基波相位角初始值。
此外,三相VSR交流侧的电流为:
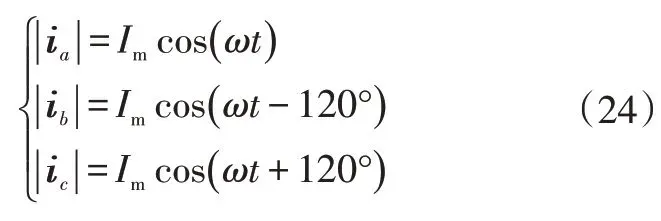
直流侧输出电流为:

可将式(23)和式(24)代入式(25),经过简化可得:
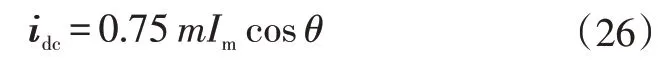
电压环控制结构如图5所示。

图5 电压环控制结构
令Kvl=Kvp/τv,Tev=Tv+3Ts,Kvl、Kvp分别为电压环的比例系数、积分系数;Tv为电压环采样周期,Tev为电压环采样时间;τv为惯性时间常数。取mcosθ=1,可得简化后电压环的开环函数为:

又有电压环频宽hv=τv/Tev,根据文献[12]工程设计方法中典型Ⅱ型系统参数公式可得:
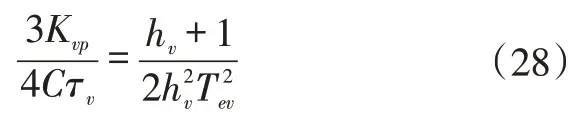
在实际工程应用中,系统的抗干扰性和跟随性均需综合考虑,再根据文献[12],取hv=5代入式(28),可得电压环PI调节器的比例和积分系数:

经上述分析确定了电压环PI 控制参数,但在实际应用中,由于设备参数不一致,还需根据实际情况进行微调,以得到最优参数值。
5 仿真对比分析
本文针对三相VSR 电路,采用电流交叉解耦的双闭环控制策略和SVPWM 的调制策略来控制功率开关管通断开展仿真,如图6 所示。针对本文研究的直流充电桩对电能质量的影响,从负载稳定运行与负载突变的角度,对仿真结果进行具体分析。

图6 三相PWM整流器矢量控制仿真
5.1 负载稳定时
图7 所示为网侧三相电流波形,由图7 可见三相电网电流相差相位、幅值保持一致,且为正弦波,实现了正弦化。其功率模块的数值显示为0.998 4,大于0.99,得到显著提高。

图7 网侧三相电流波形
图8 所示为网侧A 相电压和电流仿真波形,起振时,呈现出较大的电流过冲,这是因为直流侧母线接了较大的滤波电容。从图8 可以看出,持续约0.1 s 后,A相电压和电流保持同频同相,实现了三相PWM 整流器在单位功率因数状态运行。

图8 A相电压、电流波形
图9所示为直流侧电压输出波形,从图9可以看出,外环电压经过PI调节能够敏捷地适应外环电压指令的设定值(650 V),调节时间约为0.1 s,实现了输出电压的稳定追踪。

图9 直流侧电压输出波形
图10 所示为交流侧A 相电流谐波分析,谐波失真(THD)为0.92%,远小于5%,达到了系统设计的要求,电能质量所受干扰明显减小。
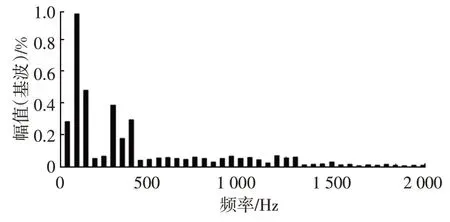
图10 交流侧A相电流谐波分析
5.2 负载突变时
负载发生突变时,主要的波动体现在三相电压电流波形和直流侧电压输出波形,分别如图11、图12所示。
在第0.1 s,负载端减少了负载链路,网侧电流迅速增加约30 A,远大于负载稳定运行时,但三相电压电流始终保持同相位,跟随性很好。
由仿真结果分析可知,SVPWM 控制电流响应速度快、系统稳定性好、谐波污染小,且在负载变动时,也能快速稳定地实现电流跟随、电压输出与减小谐波污染的目的。

图11 交流侧三相电压电流波形
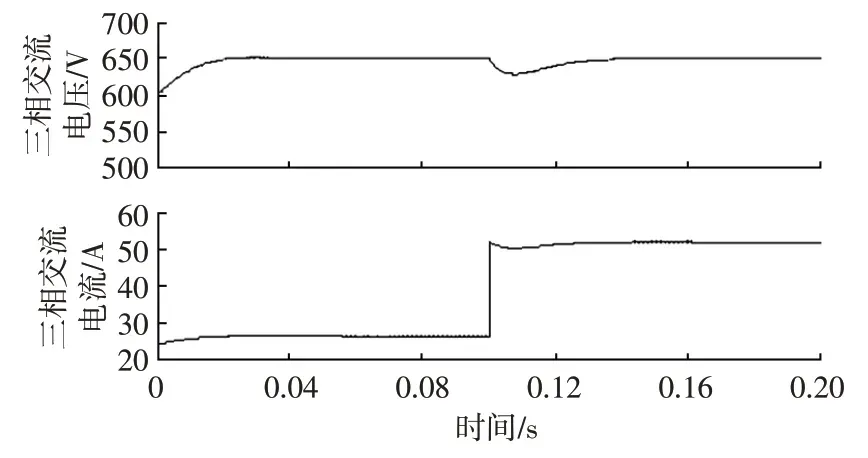
图12 直流输出侧电压电流波形
6 试验与结果分析
在以上分析和仿真的基础上,对控制策略进行实测。受实验室条件的限制,搭建的试验平台负载为1 kW,并将本文方法与不控整流测试进行对比。
6.1 不控整流测试
通过快速傅氏变换(Fast Fourier Transformation,FFT)分析可知,当工作在不控整流时,总的谐波为80.95%,如图13所示,远大于设计要求的总谐波失真低于5%的标准,其谐波污染严重,对电能质量影响严重。
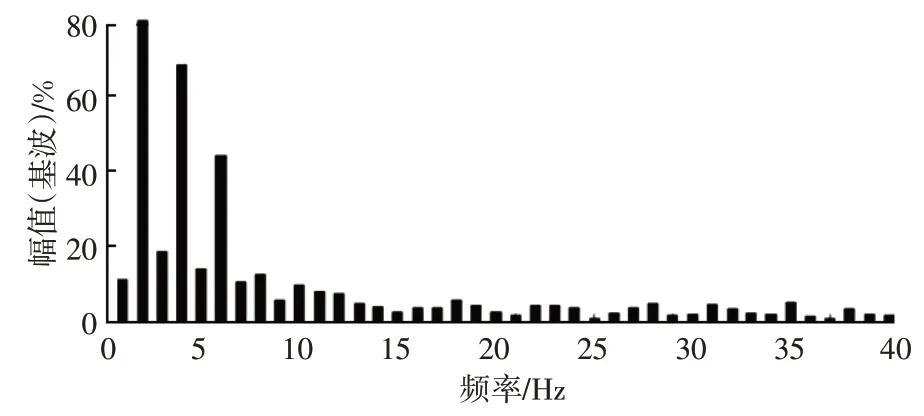
图13 不控整流谐波
6.2 搭建试验平台测试
所搭建试验平台的主要技术参数为:额定输入电压U=110 V;输入电压频率f=50 Hz;交流侧电感L=3 mH;交流侧电阻r=0.5 Ω;直流侧电容C=8 mF。
经FFT 分析,最终得到交流侧电流谐波失真为3.65%,符合总谐波失真低于5%的标准。从电流的谐波含量可以看出,APFC模块抑制了电网的谐波含量,降低了对电流质量的影响,如图14所示。
7 结束语
本文从直流充电桩自身整流模块出发,通过引入有源功率因数校正技术,实现了电网侧电流正弦化,电压和电流同相位,使系统在单位功率因数下运行并减少电网的谐波,能量能够双向流动,直流侧电压可调,从源头上抑制谐波的危害,减少直流充电桩对电能质量的影响,并通过采用MATLAB 仿真和平台搭建验证了所选策略的可行性与优势。
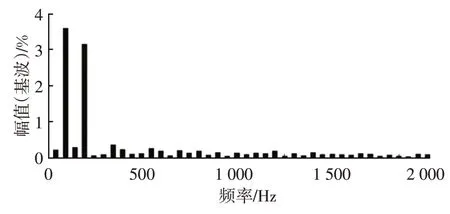
图14 交流侧电流谐波分析
