基于多模式切换的智能汽车自适应巡航控制研究*
2020-06-24刘明春涂桃黄菊花宁予
刘明春 涂桃 黄菊花 宁予
(1.南昌大学,南昌 330031;2.汉腾汽车有限公司,上饶 334100)
主题词:自适应巡航控制 多模式切换 模型预测控制 模糊控制 PID
1 前言
自适应巡航控制(Adaptive Cruise Control,ACC)系统可根据前车的驾驶状况对汽车的行驶速度进行自动调整。目前,综合考虑安全性、燃油经济性和舒适性的多目标协调ACC 系统已经面世[1-2]。然而,由于汽车行驶工况和周边车辆运动状态难以预测,ACC 系统存在频繁加、减速及车速控制不稳定等现象。多模式ACC系统有利于提高车辆在复杂工况下的安全性和舒适性,其核心在于合理的模式划分方法和切换策略。
目前,国内外对ACC 系统的模式划分和切换策略主要基于自车加速度、与前车的相对距离和相对速度等状态变量。美国PATH 项目将纵向控制分为驱动控制和制动控制[3];Fancher 等[4]应用相对车距和相对车速将ACC分为6种工况,但难以通过实车验证来标定工况划分的边界;Canale等[5]依照前方车辆的行驶状态,把ACC划分为加速、减速和匀速3 种模式,并将驾驶员的参考模型融入控制系统,但所设计的控制模式很难满足实际驾驶需要;张德兆等[6]基于零期望加速度曲线,将ACC分为定速巡航、车距保持、接近前车和超车模式,较好地解决了模式切换中的加速度突变问题,但超车模式隶属于驾驶员操作,不应存在于系统自动驾驶模式中;高振海等[7]根据自车的加速度将ACC分为巡航、稳态跟随和瞬态跟随模式,但并未充分考虑前车加速度变化对ACC系统的影响;孙晓文等[8]将ACC系统分为巡航速度控制和跟车距离控制2 种模式,提出的控制策略能够保证ACC 车辆的行车安全,但在车距与车速模式之间切换时,加速度会在短时间内超出期望值,降低了舒适性。
针对现阶段ACC系统切换模式较为简单,不能适应复杂交通状况的问题,本文提出一种基于多模式切换的ACC策略。根据自车与前车的运动关系,基于模糊逻辑划分ACC 的工作模式,在定速巡航模式中,通过PID 控制算法实现对设定速度的跟随,在跟车模式中,采用模型预测控制(Model Predictive Control,MPC)算法求解期望跟车加速度,安全、舒适地跟随前车。最后通过多种仿真工况验证所提出的ACC系统控制策略的有效性。
2 自适应巡航控制模式定义
根据前方是否存在有效目标,将车辆自适应巡航工况分为巡航和跟车2种场景,进一步根据模糊控制将纵向工况分为5 种模式,如图1 所示。引入紧急系数im衡量车辆行驶模式中的紧急程度,im为[0,1]范围内的无量纲系数,im=0 代表紧急程度最低,im=1 代表紧急程度最高。本文针对不同的自适应巡航行驶模式设置了相应的紧急系数取值范围,见表1。

图1 ACC系统总体框架

表1 车辆自适应巡航行驶模式
3 基于多模式切换的ACC系统设计
针对前述ACC模式,本文设计的控制策略如图1所示。
车头时距th指在同一车道上行驶的车辆队列中,连续两车辆车头端部通过某一断面的时间间隔,th的临界值为临界车间时距Thc。模式划分模块根据Thc、两车之间的动态信息(包括车辆实际间距d、间距误差Δd、相对速度Δvx)基于模糊逻辑进行模式划分,以适应复杂的动态交通系统。控制期望求解模块根据不同的控制模式采取相应的算法求解满足安全性、舒适性需求的期望自车加速度ades,作用于被控车辆,实现ACC系统的功能。
3.1 基于PID的定速巡航模式控制
定速巡航模式下,采用PID算法计算期望加速度:

式中,kP、kI、kD分别为比例项、积分项、微分项系数;vxset为驾驶员设定的巡航车速;vx为车辆纵向速度。
3.2 基于MPC的跟车模式控制
3.2.1 纵向跟车运动学建模
在ACC 系统中,实际加速度和期望加速度满足一阶惯性时滞关系[9-10]:
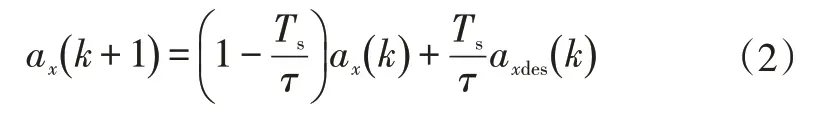
式中,τ为惯性时间常数;Ts为系统的采样周期;axdes为上层控制算法求解得到的期望加速度;ax为车辆实际纵向加速度;k为采样点序号。
纵向跟车运动学模型如图2 所示。根据车间纵向运动学关系,有如下关系式:

式中,vpx为前车的纵向速度;apx为前车的纵向加速度;为自车加速度变化率。

图2 车辆纵向跟车运动学模型

3.2.2 预测方程与目标函数
MPC算法可以预测未来p时刻内两车间距和相对速度,并将该预测值与期望值进行比较,求得最优控制序列。假设系统状态可以通过测量得到,并设定以下条件:
a.假定p为预测时域,m为控制时域,满足p≥m。
b.假设控制时域之外控制量不变,即:

c.假设外部干扰在预测时域内保持不变,即:

由此,定义m步的控制输入向量为:

定义p步内系统的预测输出矩阵为:
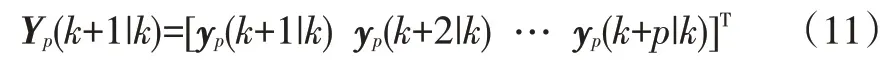
根据式(7),得到预测方程具体的表达形式为:

与式(11)相对应,参考输入应在整个预测时域p内实时更新,定义参考输入序列为:

式中,r(k)为参考输入量。
本文研究主要针对稳定跟车性能和舒适性。稳定跟车性能需满足两车间距为期望间距,且本车与前车速度一致,舒适性由加速度进行评价。定义目标函数为:
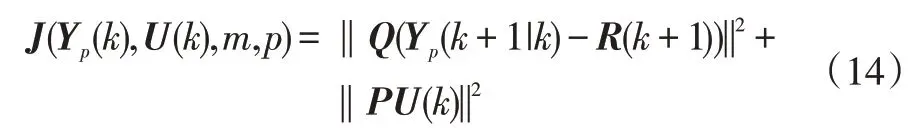
式中,Q=diag(qΔd,qΔv,qaf,qjerk);qΔd为车间距误差的权重因子,其值越大,两车的实际车间距越接近于安全车间距模型计算的期望车间距;qΔv、qaf、qjerk分别为两车的相对速度、本车加速度以及加速度变化率的权重因子,权重因子越大,相应变量的值越小;P=diag(qaf,qjerk),其选取影响控制量,即MPC 控制器决策出的期望加速度及其增量,值越小,对应的控制量越大。
本文综合考虑跟车性、舒适性与燃油经济性,为提升对不同交通场景的适应性,选取不同权值,令跟车性权重系数Γy=qΔd=qΔv,舒适性权重系数Γu=qaf=qjerk。
定义与控制序列无关的向量:

可推导出:
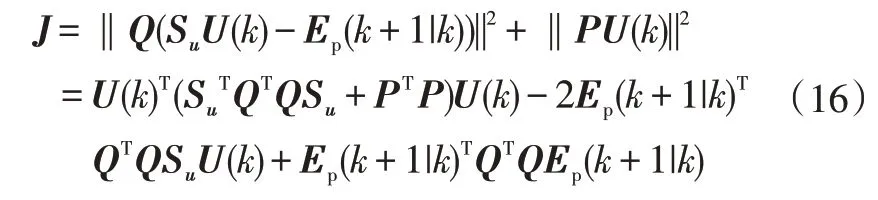
忽略控制量无关项Ep(k+1|k)TQTQEp(k+1|k),进一步推导出:

式中,H=SuTQTQSu+PTP;G(k+1|k)T=2SuTQTQEp(k+1|k)。
3.2.3 约束条件
3.2.3.1 安全性
两车间距大于安全车距dc:

3.2.3.2 跟踪性
稳态跟车时,两车间距趋近于期望间距,相对速度趋近于0:

3.2.3.3 舒适性
大量针对驾驶员的主观评价与行车数据表明,车辆加速度在-2~2 m/s2范围内可以保证较好的舒适性[12-13]。因此,文本选取本车加速度ax(k)作为ACC 系统舒适性的量化表征参数,并对其进行如下约束:

式中,axmin、axmax分别为最小、最大加速度。
3.2.3.4 经济性
车辆速度变化越平缓,燃油经济性越高,因此对自车的控制变量,即期望加速度进行限制:

式中,umin、umax分别为控制变量的最小、最大值。
3.2.3.5 速度
考虑到自车的能力限制和交通法规的限制,车辆行驶过程中还需要满足速度约束:
在本研究中原先设立了一种假设,就有形和无形的因素,超市供应链参与者农民比非参与者农民要过得好。由于农民采用的市场渠道,定量分析没有揭示销售、收入、业绩和整体状况的显著差异。然而,在超市供应链销售的农民比即时交易市场中的农民更满意并且获得相对较高的售价。此外,定性信息表明,以评估条款为标准,在超市供应链销售的农民过得比即时交易市场中的农民要好,但是,关于影响程度需要进一步的分析以达到结论性的结果[5]371-388。

式中,vxmin、vxmax分别为最小、最大车速。
3.2.4 约束及目标函数处理
定义约束条件下的输出yb(k)为系统的5个状态,即:

式中,Cb=diag(1,1,1,1,1)为状态空间方程系数矩阵。
基于式(23),定义约束条件下的输出为矩阵形式:
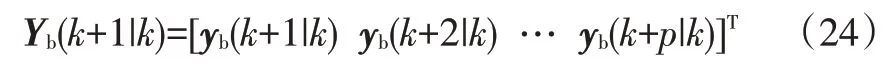
与预测方程式(12)一致,得到约束条件下的预测方程表达式为:

定义系统输出的约束条件为:

同理,定义控制变量的约束为:

考虑到上述输出变量和控制变量的硬约束可能导致优化求解过程中出现无可行解的情况,引入向量松弛因子来软化硬约束[14-15],并将性能指标函数和约束条件进行预测型转化,转化为求解带有约束的二次规划问题:
a.增加系统输出约束的软化因子ςymin和ςymax:

式中,ςΔdmin、ςΔvxmin、ςvxmin、ςaxmin、ςa′xmin、ςΔdmax、ςΔvxmax、ςvxmax、ςaxmax、ςa′xmax分别为系统系统状态变量的硬约束最小值、最大值的松弛系数。
b.增加系统控制约束的软化因子ςumin和ςumax:
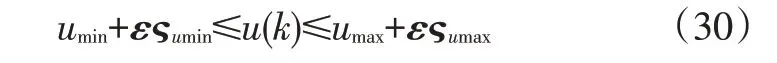
软化后的约束不能被无限放大,在目标函数式(17)中增加代价函数,对松弛因子进行限制:

式中,ε=[ε1ε2ε3]T为向量松弛因子,限制软化后的输出约束和控制约束,ε1=0,ε2≥0,ε3≥0;γ=diag(γ1,γ2,γ3)为惩罚矩阵系数,调节目标性能的权重,γ1>0,γ2>0,γ3>0。
优化问题式(31)可转化为求解约束条件下的二次规划问题,将式(31)写成标准二次型约束优化问题,得到:

4 基于模糊规则的跟车性能调节及模式切换
由于实际驾驶环境复杂多变,单一跟车模式的控制参数无法满足车辆实际行驶工况。车辆控制参数需要在稳定跟车性能与舒适性之间进行调节,此外,不同的跟车模式对应不同的紧急系数。本文基于自车与前车的车间距误差Δd和相对速度Δvx设计模糊规则,一方面调节目标函数式(14)中的权重系数Гy和Гu,以调节跟车过程中舒适性和跟车性的权重,另一方面计算跟车过程中的紧急系数im,切换跟车模式。性能权重系数与跟车紧急系数密切相关:在紧急系数高的模式下,应当以稳定跟车性能为主,以保证跟车安全性;在紧急系数低的情况下,应当以舒适性能为主,以保证跟车舒适性。
4.1 输入变量模糊化
模糊控制器的输入为Δd和Δvx。将Δd模糊化为MS(微小)、S(小)、M(中)、MB(较大)、B(大)5 个集合,并设定其变化范围为[-80,80]m;将Δvx也分为MS(微小)、S(小)、M(中)、MB(较大)、B(大)5个等级,本文设定车速范围为[0,120]km/h,Δvx的模糊论域变化范围为[-20,20]m/s。输入变量Δd和Δvx的隶属度函数如图3所示。

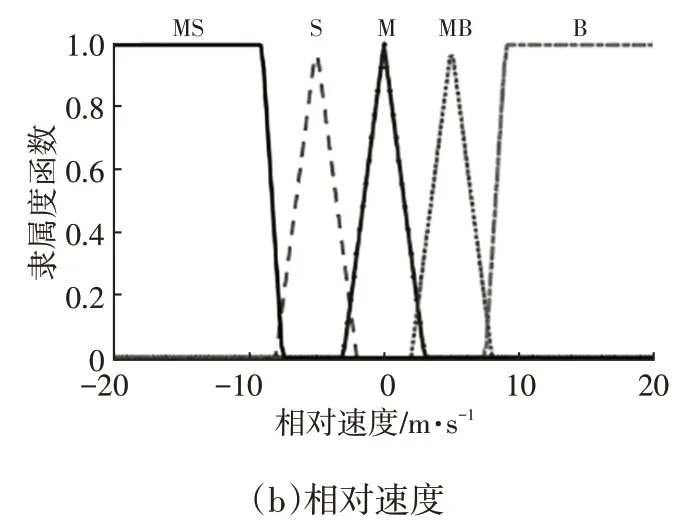
图3 输入变量隶属度函数
4.2 输出变量模糊化
模糊控制器的输出为权重系数Гy和Гu,以及紧急系数im。Гy和Гu具有相对意义,在此将Гu固定为1,调节Гy。将Гy模糊化为S(小)、M(中)、MB(较大)、B(大)4个集合,变化范围为[0,5]。将紧急系数im模糊化为MS(微小)、S(小)、M(中)、MB(较大)、B(大)5个集合,变化范围为[0,1],其Гy和im的隶属度函数如图4所示。

图4 输出变量隶属度函数
4.3 模糊规则设计
根据交通场景分析,如果两车间距远大于期望间距,则Δd处于B(大)论域,无论Δvx如何变化,都认为二者处于相对安全的区域,此时适当提高舒适性的权重,跟车性的权重则相对降低,即Гy处于MS(微小)论域或者S(小)论域,且随着相对速度的增加,该值处于论域S(小)的可能性增加。如果两车间距在期望间距附近,Δd处于M(中)论域,则随着Δvx的增大,两车间的距离会越来越大,对于跟车性的要求则越来越低;相反,如果后车车速大于前车,二者间距会越来越小,危险程度则越来越高。因此,随着Δvx的增大,Гy由MB(较大)逐渐向S(小)过渡。如果两车间距较小,Δd处于MS(微小)论域,而后车的速度大于前车,相对速度Δvx处于MS(微小)论域,则车辆行驶状况较为紧急,因此稳定跟车性能成为首要考虑的因素,Гy由B(大)逐渐向MB(较大)过渡。综上,设计模糊控制器的模糊规则如表2所示。

表2 权重系数调节模糊控制规则表
采用重心法将模糊规则进行解模糊化运算,分别得到Гy和im关于Δd和Δvx的三维曲面图,如图5所示。基于上述模糊规则,可以基于Δd和Δvx得到Гy和im,完成跟车性能调节和跟车模式切换。

图5 输入-输出变量的三维曲面图
5 控制系统仿真及分析
本文通过多种工况下的仿真验证所设计的多模式ACC策略的有效性。系统主要控制参数如表3所示。
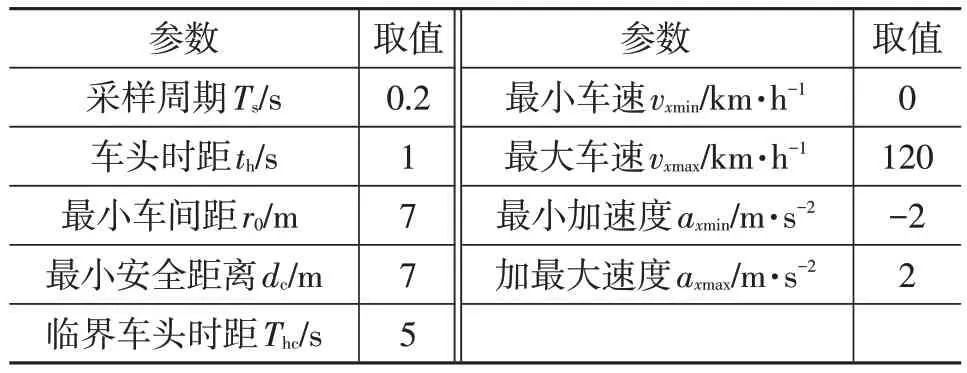
表3 控制系统主要参数
5.1 工况1:前车变速
设前车开始以40 km/h 匀速行驶,在第70 s 加速至60 km/h 匀速行驶,再减速至40 km/h 后匀速行驶,自车与前车初始车距为300 m,以60 km/h接近前车,仿真结果如图6所示。其中,自车的状态由自车运动方程计算得到,前车的状态由基于自车的传感器测量得到。
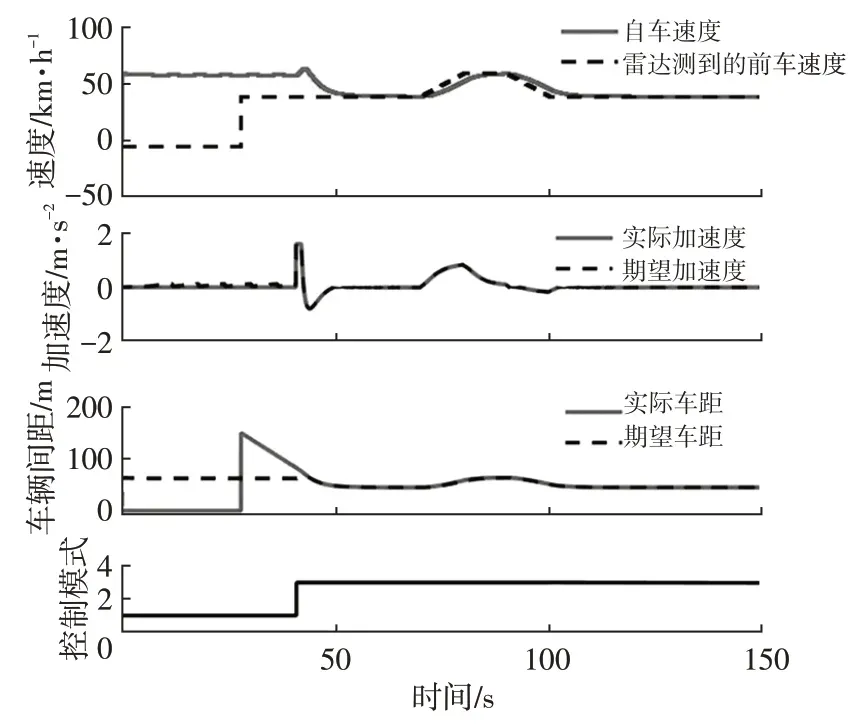
图6 前车变速工况ACC仿真结果
图6中,前车速度和实际车距在第27 s前显示为0,这是由于自车传感器的最大检测距离为150 m,该时间段内前车不在自车的检测范围内,车辆工作在模式1。第27 s时,实际车距为150 m,前车进入自车传感器的检测范围。第40 s后自车与前车距离为期望车间距,车辆工作在模式3,由MPC控制器求解得到的自车实际加速度可以很好地跟踪期望加速度,且跟车过程加速度变化较平顺,保证了较好的舒适性。与此同时,自车速度从60 km/h平稳地降低到40 km/h后跟随前车行驶,并将实际车距保持在期望车间矩以保证较好的跟车性能。
5.2 工况2:前车切出
设前车以40 km/h 匀速行驶,自车与前车初始距离为100 m,自车车速60 km/h 向前行驶,前车第25 s 时切出当前车道,换道至旁侧车道,仿真结果如图7所示。

图7 前车切出工况ACC仿真结果
由图7 可知:仿真开始后,自车传感器迅速检测到前车,在第25 s 前减速逐渐接近前车,并稳定跟随前车(跟车模式3);第25 s时前车切出当前车道,不在自车传感器检测范围内,故此时的前车速度和车辆间距为0;第25 s后车辆恢复工作模式1,自车速度逐渐恢复至设定车速60 km/h。自车加速度由MPC 控制器计算得到,车辆在第25 s 前减速接近前车,以及第25~33 s 加速恢复至设定速度的过程中,加速度都在[-1,1]m/s2范围内,保持了较好的舒适性。
5.3 工况3:前车切入
设置前车在旁侧车道以40 km/h 匀速行驶,自车以60 km/h匀速行驶,与前车相距200 m,第6 s时前车从旁侧车道切入自车所在车道,仿真结果如图8所示。

图8 前车切入工况ACC仿真结果
由图8可知:在第6 s时前车切入自车所在车道后,由于距离较远,自车并未立即减速,ACC 系统工作在模式1;当与前车距离在第13 s 达到期望车间距65 m 后,自车开始减速;当自车速度在第25 s 减速至40 km/h 与前车一致后,便以该速度稳定跟随前车行驶,ACC 系统工作于模式3。自车加速度变化情况由MPC 控制器计算得到,车辆在第13 s 时开始减速,且减速过程中减速度逐渐收敛至0,保持了较好的舒适性。
5.4 工况4:NEDC-市郊工况
新欧洲行驶循环(New European Driving Cycle,NEDC)工况包括车辆行驶的典型市区工况和市郊工况,本文选取NEDC中的市郊工况验证ACC系统的有效性。在仿真过程中,自车与前车在同一车道上行驶;仿真开始时前车静止,自车以60 km/h驶向前车;第10 s时前车起动,并根据NEDC中的市郊工况控制车速,自车在ACC系统的控制下跟随前车行驶。仿真结果如图9所示。
由图9 可知,在第10 s 时,自车与前车相距150 m,前车进入自车传感器的检测范围,但由于距离较远,自车并未减速,仍工作在定速巡航模式;第20 s 时,车间距为65 m,自车在ACC 系统的作用下开始减速,并在第25 s 时减速至与前车速度一致;之后自车稳定地跟随前车加速和减速,ACC 系统工作在模式3,即稳态跟车模式。由图9 可知,整个工况中自车加速度基本在[-1,2]m/s2范围内,保持了较好的跟车舒适性。

图9 NEDC-市郊工况ACC仿真结果
6 结束语
本文针对复杂工况下智能汽车自适应巡航控制的问题,设计了一种基于多模式切换的自适巡航控制方法。基于车辆纵向跟车运动学关系,划分了自适应巡航过程中的行驶模式,并采用紧急系数表征各行驶模式下的危险程度,较完整地描述车辆纵向跟车过程中的ACC各种工作模式。采用PID 控制算法进行定速巡航模式下的控制;采用MPC算法进行跟车模式下的控制,并设计了模糊控制器调节MPC 中性能指标函数的权重值,同时计算不同跟车状态下的紧急系数,实现了不同工况下稳定跟车性能和舒适性的协调,以及ACC 不同控制模式之间的切换。多种工况下的仿真结果表明,所设计的多模式切换控制方法有效实现了车辆在各种工况下的跟车性能和舒适性的协调,取得了优良的控制效果。
