土钉支护边坡的极限平衡法分析

摘要：极限平衡法是边坡稳定性分析中常用的方法。本文分析了坡度为45°和60°情况下，分别采用在0°、15°和30°三种不同坡度土钉加固。对比分析安全系数、临界滑动面和钉力等稳定性参数。极限平衡法具有更高的安全系数。

Abstract： The limit equilibrium method is a commonly used method in slope stability analysis. This paper analyzes the use of soil nails with three different slopes at 0°， 15° and 30° when the slope is 45° and 60°， contrasts and analyzes stability parameters such as safety factor， critical sliding surface and nail force. The limit equilibrium method has a higher safety factor.

关键词：极限平衡;有限元;安全系数;滑动面;钉力

Key words： limit equilibrium;finite element;safety factor;sliding surface;nail force

中图分类号：TU476                                      文献标识码：A                                  文章编号：1006-4311（2020）15-0160-04

0  引言

土钉支护已成为一种有效的边坡支护技术。采用土钉支护技术，可以改善边坡的稳定性。加筋边坡的稳定性分析一直是许多研究者采用传统的极限平衡法进行的。这些极限平衡法也称为“切片法”，是基于将破坏质量分成切片的概念，并对层间力分布进行一定的假设，以计算安全系数。这些假设通常集中在层间力的倾角或位置以及假定几何体（如对数螺旋、楔形和圆形）的预先选择的滑动面上。

本文试图用SLOPE/W软件分析土钉支护边坡的响应。在45°和60°不同坡度条件下，采用0°、15°和30°的土钉水平倾角，对土钉支护边坡进行了数值模拟。分析安全系数、破坏滑动面和钉力。

1  极限平衡法加固边坡稳定性分析

1.1 基于SLOPE/W的建模与分析

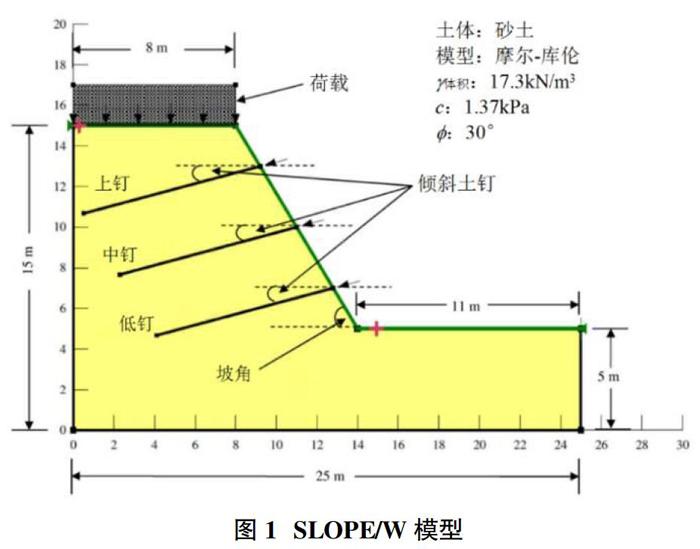
本文采用45°和60°两种不同的坡度边坡进行了模拟。用土钉加固，土钉倾斜角度分别为0°、15°和30°。SLOPE/W包通过定义土坡的区域来实现土坡的施工。用于实验研究的边坡模型的尺寸按比例缩小，并采用1cm∶0.5m的比例输入模型SLOPE/W中。

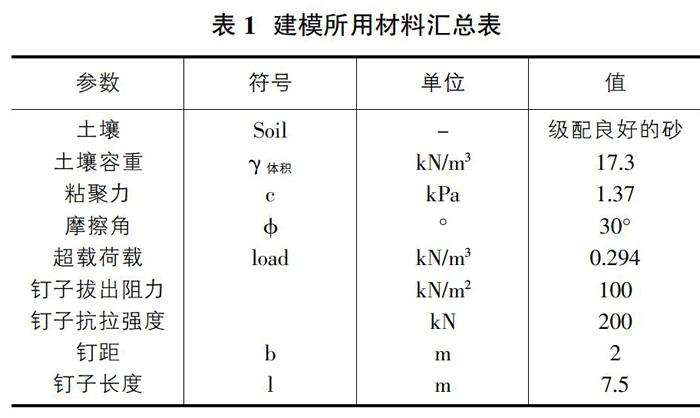
边坡加固的研究主要是采用钉单元进行的。分析中使用的模拟模型如图2所示。在极限平衡包中的所有其他方法中，分析是通过Morgenstern-Price方法进行的，该方法使用层间剪力和层间法向力之间的关系。分析中选择的层间函数是一个半正弦函数，其安全系数分布计算为常数。表1总结了模型中使用的土壤和土钉特性。

1.2 边坡安全系数

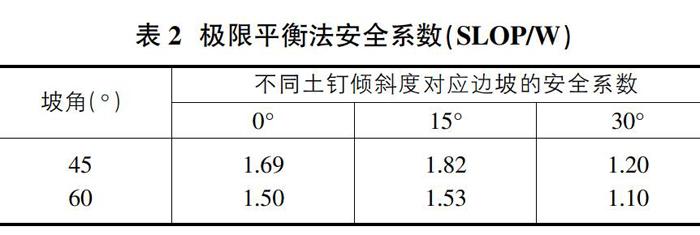
对于45°的坡度和15°的土钉倾斜度，用极限平衡法计算的安全系数为1.82。同样，对于60°的坡度，当钉子倾斜15°时，安全系数最高为1.53。从表2可以看出，安全系数从0°到15°增加，从15°到30°减少。在45°和60°的坡度角下都观察到这种模式。SLOPE/W采用的Morgenstern-Price方法使用k值来检查结果的收敛性。

2  边坡破坏滑动面

从图2（a）、（b）和（c）可以看出，对于45°的加筋边坡，产生了圆形滑动面。在钉子倾斜0°和15°的情况下，滑动面穿过整个顶部。当钉子倾斜30°时，可以观察到更小的滑动面。滑动面的黑色阴影部分表示具有相同安全系数的试验滑动面带。

对于60°斜坡，从图3（a）、（b）、（c）可以看出滑动面是圆形的。对于土钉倾角为0°和15°的斜坡，安全系数的变化很小。这是由滑动面的黑色阴影部分表示的。而30°土钉斜加固的60°边坡滑动破坏较小，临界滑动面靠近边坡面。

3  土钉轴向力分布

从图4（a）、（b）中可以看出，0°、15°和30°的底部钉承受45°和60°斜率的最大钉轴向力。对于0°和15°的钉子倾角，轴向力从上钉到中钉增加，下钉最大。而对于30°斜钉45°斜面，在上、中、下钉中发现轴向力为100kN。同样，在60°坡度中，上、中、下钉的轴向力为66.66kN，30°钉倾斜。100°kN的最大轴向力在45°倾斜的底部钉中，在30°处钉倾斜。在60°坡度下，钉头倾斜度为0°的底钉承受最大轴向力为71.67kN。

4  土钉长度对边坡稳定性影响

通过对边坡的分析，发现在滑动破坏过程中，模拟和移动的钉子长度随着钉子的倾斜和位置的变化而变化。所有倾斜0°、15°和30°的钉子最初都是用7m的恒定长度换算成比例进行建模的。SLOP/W分析得出，在两个坡度角中，30°的钉子倾斜，使不到50%的钉子长度移动，以抵抗坡度破坏。对于另外两个0°和15°的钉子倾斜，发现超过90%的釘子长度被用来抵抗剪切作用。结果表明，如果破坏面采用最大钉长，则钉的强化作用被完全调动。表3给出了活动钉子长度百分比的汇总。加筋边坡的LE分析也说明了土钉的荷载传递机制是由土钉的抗拔力或抗拉能力决定的。

对于45°坡度上的30°钉子倾斜度，钉子被发现断裂，用虚线表示（图5）。这也代表了这样一个事实：钉子已经完全利用了它的拔出能力，现在正在通过它的拉伸能力转移荷载。如图6所示，在60°加筋边坡和30°加筋边坡中观察到类似的钉荷载传递机制模式。

LEM分析中观察到最大钉力在底部钉，LEM预测45°比60°坡角处的底钉力大。这可能是由于覆盖层随着深度的增加而增加。顶部土钉承受坡顶覆盖层，底部土钉承受最大法向力，因此承受较大的剪切力。剪切力的增加导致底部土钉的轴向力增大。因此，在LEM 60°坡脚处，土钉的钉力较低可归因于荷载传递期间土钉的失效。

5  结论

通过本文的研究，得出以下结论：

①极限平衡法分析结果均表明，最稳定的边坡为15°钉斜水平加筋边坡。②土钉倾角的增加不会增加边坡的稳定性。在0°～15°范围内，随着钉子倾角由15°～30°的变化，坡度FOS逐渐增大。③极限平衡法的最危险滑动面位于离边坡较远的位置。④极限平衡法计算的钉力值较高，且随钉位的变化而变化。⑤极限平衡法能预测钉子荷载传递机理中的极限状态，即拔出能力、拉伸能力或面层能力。破坏面与钉子长度的交点决定了哪种情况已经被激活。⑥极限平衡法的结果取决于钉长和键长。具有较长钉粘结长度的斜坡比没有粘结长度的斜坡更稳定。

参考文献：

[1]连镇营，韩国城，陈庆涛.土钉支护弹塑性数值分析及稳定性探讨[J].岩土力学，2002，23（1）：85-89.

[2]梁向前，程敦伍，陈庆涛.土钉支护的有限元模拟[J].地基基础工程，2003，6（11）：29-31.

[3]赵国景，崔岩，吴世红.土钉支护有限元计算方法研究[J].工程力学，2001，18（4）：145-150.

[4]孙宗军，陈新华，庞吉莲，朱业飞.土钉支护中土钉与土作用机理数值分析[J].建筑技术，2004，5（35）：344-345.

作者简介：刘海涛（1986-），男，宁夏灵武人，本科，学士，工程师，研究方向为岩土工程。