BOPPPS教学模式在大学物理实验绪论课中的应用

范金娜

（中北大学 理学院，山西 太原 030051）

物理学是一门以实验为基础的学科，物理实验是检验物理理论正确与否的试金石．大学物理实验是高等学校理工科专业学生接受基本科学训练的必修课程，是与大学物理理论课并列的课程，可为学生从事科学实验等研究打下基础．同时，大学物理实验是一门被国家教委列为单独设课的实践类课程，也是国家教委指定验收的基础课中唯一的实验课[1]．在大学物理实验的教学中，将误差理论与实验数据处理等内容放在绪论课讲述，因应用到高等数学知识并涉及较多的推导，学生普遍兴趣不高，反映内容比较抽象，不容易掌握，尤其是数据处理部分．作为学生接触大学物理实验的第一堂课，绪论课教学效果的优劣不仅影响到学生对物理实验的兴趣，也直接关系到学生日后学习中实验数据处理的好坏，故绪论课教学在物理实验教学中起着极为重要的作用．通过4个学时的理论教学，要使学生掌握物理实验课程的目标、测量误差和数据处理的方法以及实验报告的撰写等，可谓“时间短、任务重”．因此，怎样在有限的时间内将绪论课的内容给学生讲清楚，是物理实验课教学中值得思考的问题．本文将BOPPPS模式的教学理念引入大学物理实验绪论课的教学中，达到了激发学生兴趣，提高整个大学物理实验课程教学效果的目的．

1 BOPPPS教学模式

BOPPPS是以学生为中心、以教学目标为导向的教学模式，起源于加拿大教师技能培训工作坊，通过对整个课程教学的过程进行模块化分解，使学生在教学过程中积极主动地参与到课堂中来[2]．

BOPPPS教学模式将传统的课堂教学分解为6个模块，即：导言B（Bridge-in）、学习目标O（Objective）、前测 P（Pre-assessment or Pre-test）、参与式学习 P（Participation learning）、后测 P（Post-assessment or Post-test）和总结S（Summary）[3]．通过将教学过程进行模块化分解，每一个模块完成特定的教学任务．导言B把即将讲授的课程内容与学生的认知内容建立联系并激发学习的兴趣；学习目标O明确在课程学习结束时应掌握的知识与技能，是教师教学过程中应重点关注的内容；通过前测 P，可知晓学生对本节课程内容所涉及知识的掌握程度，便于教师在课堂教学中对教学内容进行针对性地设计；参与式学习P则要求学生能够积极主动地投入到课堂学习中，是整个BOPPPS的重要环节；后测P则能帮助教师定量检测学生对学习目标的达成情况；总结S则能帮助学生对本阶段所学知识进行回顾和梳理，更好地提高学习效果．

2 BOPPPS模式在大学物理实验绪论课中应用

BOPPPS模式的教学理念已被广泛地应用于物理理论课的课堂教学中，但BOPPPS在大学物理实验课（尤其是绪论课）中的应用则鲜有报道．大学物理实验课程的教学改革也被大家广泛研究[4-9]，在实验课教学中，间接测量量的实验数据处理作为数据处理中重要的部分，在绪论课的教学中是重中之重．本文以间接测量量的实验数据处理实验为例，把BOPPPS模式的六步教学法应用到大学物理实验绪论课中．

2.1 导言B

物理教学要求很强的前后逻辑性，利用这种逻辑能逐步地增强学生对知识前后连贯性的掌握．利用BOPPPS，在整个课程设计环节可充分体现这一特点．

利用多媒体展示测量仪器——游标卡尺或螺旋测微器、电子天平，并提问学生图中展示的仪器可用来测量哪些物理量，学生会很自信地回答：长度、质量．通过这2个熟悉的仪器可增加学生对课程内容的亲切感、减少距离感，提高学生的兴趣，进而引出对于与长度、质量相关的体积甚至密度等物理量．尽管不能对体积、密度等进行直接测量，但其却与可直接测量的物理量有函数关系．那么，对于这些测量量的实验数据应该如何进行处理，通过这一系列的问题引发学生思考，激发学生的兴趣，进而引出本节课内容——间接测量量的实验数据处理．

2.2 学习目标O

能够计算间接测量实验数据的不确定度及相对不确定度；能够准确写出间接测量量的真值表达式．

2.3 前测P

直接测量量的实验数据处理已经在之前课程中讲授且在本次课堂中要进行应用，故前测部分对直接测量量的实验数据处理进行简单测验，既是验证学生对所学知识的掌握程度，也是对学生的基础进行评估．特别提醒学生直接测量x的总不确定度xσ与A类不确定度sx和B类不确定度ux的关系[10]

记忆方式可归结为3个字——“方和根”．

2.4 参与式学习P

参与式学习可采用教师讲解的同时，学生回答相关问题的方式．无论是直接还是间接测量的实验数据处理，最终目的都是写出真值表达式．本节内容开始根据直接测量量的真值表达式，让学生自行写出间接测量量F的真值表达式，利用教学目标导向使学生跟随教师的思路一步步寻找每个部分的答案，增强学生求知的欲望．要达到本节课的最终目标——间接测量量的真值表达式，首先写出间接测量量F与直接测量量x1,x2的关系

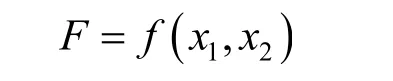
其中：将x1,x2的平均值代入即可得．不确定度σF的计算则是本节的重点，利用高等数学中全微分的相关知识可得不确定度σF公式为

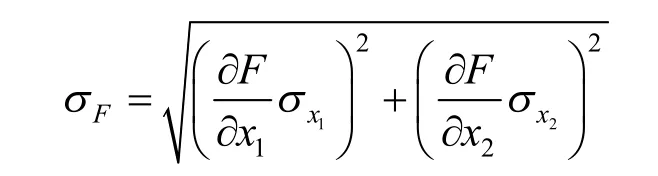
也是“方和根”形式．根据绝对误差和相对误差的关系引出相对不确定度，进而得出相对不确定度公式为

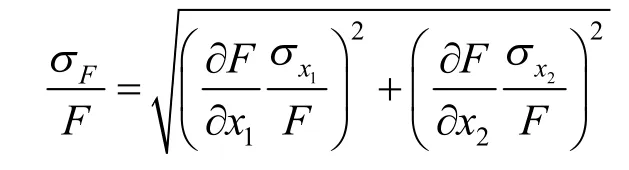
2.5 后测P

后测部分通过例题形式开展，关键是让学生参与进来．如例题内容为测量长方体小木块的密度ρ，其中质量m和长方体的长l、宽d、高h的真值表达式已经给出，并让学生利用不确定度σF的公式和相对不确定度σF/F的公式分别计算．学生会发现首先计算相对不确定度会更为方便，从而引出当间接测量量与直接测量量满足乘除关系时应该先计算相对不确定度，再计算总的不确定度的处理技巧；同时学生也通过自己推导得出密度ρ相对不确定度的表达式为

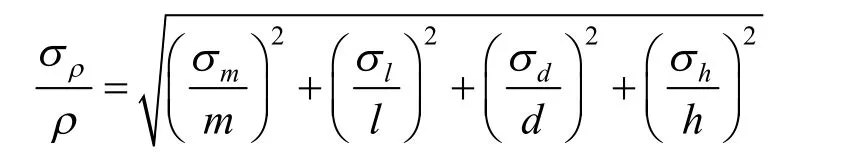
间接测量量的相对不确定度是各直接测量量相对不确定度的“方和根”，与前测中“方和根”的记忆方式相呼应．

2.6 总结S

总结是对整节课堂内容的概括，要简短而有力．学生通过此部分，可以检测最初设定的学习目标是否全部达成．完成后测部分的习题，则总结部分可相对轻松达成．

3 结语

BOPPPS六步法教学模式注重以学生为中心、教师为主导、目标为导向，一改以往“满堂灌”的教学方式，让学生参与到教学的全过程．通过在大学物理实验绪论课中的应用，极大地激发了学生学习的兴趣，充分提高了学生学习的积极性，为后续物理实验报告的数据处理奠定了良好的基础．