广义积分的求解

高亮

（安徽国际商务职业学院 信息工程学院，安徽 合肥 231131）

广义积分的定义与计算思维在整个数学知识构造中占据着非常重要的地位，不仅在无限函数求解上能够带来重要促进作用，在数理统计和微分方程等求解上也均有广泛的应用[1]．然而，广义积分在实际应用中还存在较多问题，如概念抽象、函数形式多变和计算方法难以掌握等．如果仅通过定积分的计算思路进行求解，有可能对于大部分问题而言是行不通的，更难达到有效解决实际问题．因此，可以通过总结与深入研究特殊形式广义积分计算方法，统筹对称函数、可转变函数等经常出现的积分形式，建立有效的计算体系．这样不仅能够帮助学生更快速地掌握解题的思路，还能够检验运算过程合理性，对广义积分求解的研究具有非常重要的实际意义．

1 广义积分基本求法

由广义积分的定义式可知，定积分的计算方法可以移植给广义积分．于是，广义积分计算中，同样也有牛顿-莱布尼茨公式、换元积分法和分部积分法．

1.1 牛顿-莱布尼茨公式

1.2 换元积分法

1.3 分部积分法

2 广义积分的特殊求法

对于广义积分，一般计算方法只能够解决部分函数计算，根据不同计算函数以及收敛情况可以相应地进行函数转变，从而简化计算过程，实现复杂函数积分的求解．如利用函数的对称性、Γ函数和β函数、重要极限、留数定理、级数展开法以及含参变量积分等来计算．

2.1 利用函数的对称性计算

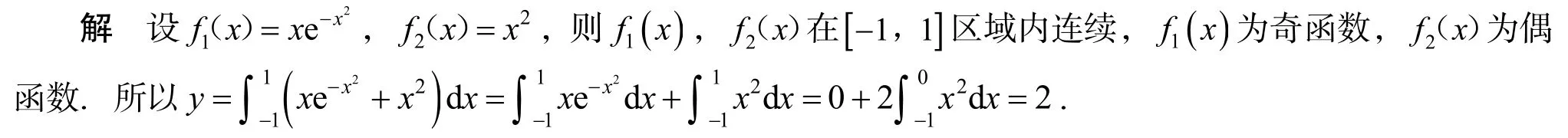
2.2 利用Γ，β函数计算

2.3 利用重要极限计算

2.4 利用留数定理计算

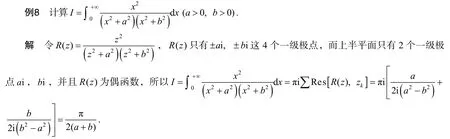
2.5 利用级数展开法计算

利用无穷级数计算广义积分也是常用的一种技巧，可以将无穷区间上的广义积分表示成级数形式来求积分．

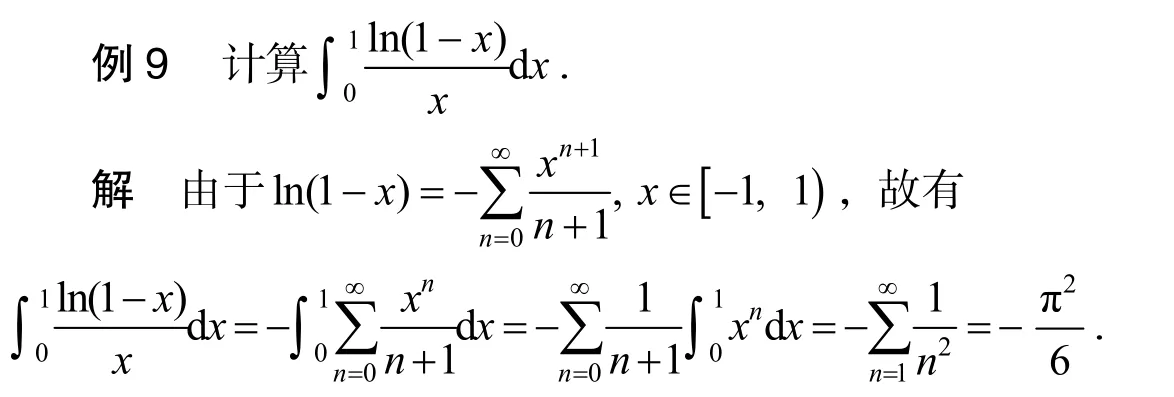
2.6 利用含参变量积分计算

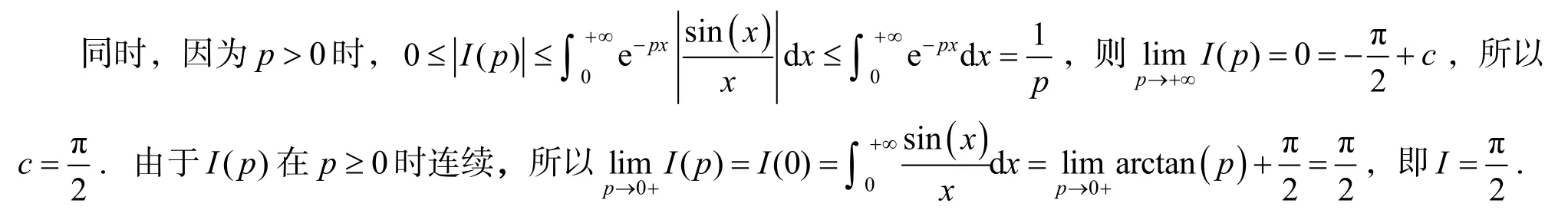
3 结语

综上所述，广义积分求法可以从不同的知识点、不同的角度去理解．针对不同的广义积分，不仅可以使用换元积分求法和分部积分求法等基本方法，还可以利用函数的对称性、Γ函数和β函数的性质、泰勒公式的展开等方法进行运算，深度挖掘与开发新方法解决广义积分求解是当下研究热点．然而，我们更应当学会选择适当的方法来求解相应的广义积分．