电主轴在机可靠性试验和评估方法研究

□ 辛庆伟 □ 周大朝 □ 邢诺贝 □ 刘福军 □ 许黎明

上海交通大学 机械与动力工程学院 上海 200206

1 研究背景

随着传动技术的发展,电主轴的整体水平越来越高,其精度保持能力、寿命及可靠度指标都得到大幅提升,故障间隔时间往往超过数千小时。现行电主轴可靠性验证主要有定时截尾试验、可靠性强化试验等,定时截尾试验需要面对试验期间无故障出现的问题,可靠性强化试验通常多用于试验研发阶段激发产品的潜在缺陷。电主轴可靠性试验通常需要对选取的样本采用专用模拟加载装置进行配合试验,多用于产品接收阶段或者研发阶段,难以运用到实际生产中。为此,笔者对加工中心的电主轴进行在机加速加载试验,开展对电主轴在机可靠性试验和评估的研究。

要实现电主轴的在机可靠性试验和评估,需要解决两个主要问题:① 选取和采集能够反映电主轴性能退化的特征量;② 通过性能退化数据评估电主轴的失效时间。

加速退化试验最早于20世纪80年代被提出。Lu Jye-Chyi等[1]最先提出利用产品的性能退化量开展可靠性试验及评估。赵建印等[2]基于性能退化数据,对累积损伤过程下的产品退化失效进行了建模分析。迟玉伦等[3]利用声发射传感器采集电主轴性能退化数据,对电主轴进行可靠性研究。蒋喜等[4]将退化理论应用于电主轴的可靠性研究,得到电主轴的伪失效寿命,以此来进行可靠性评估。在性能退化数据收集方面,邬再新等[5]应用LabVIEW软件开发了高速电主轴试验台数据采集系统,实现了在试验台上对电主轴试验过程中电流、转矩、转速等主要参数的采集。陆建明等[6]研发了数字化数控机床主轴测试系统,集成了各类检测功能,实现了电主轴测试数据采集的实时性和精确性。电主轴性能退化特征量的选择一般基于对电主轴失效机理的分析。张玥等[7]分析了润滑系统的故障情况,并提出了改进措施。王红军等[8]选择电流作为电主轴性能退化量,建立了电主轴性能退化模型。邱荣华等[9]将径向跳动作为退化量进行可靠性试验,但由于电主轴样本量较少,在可靠性指标的评估上存在一定难度。文献[10-12]对小样本情况下的电主轴可靠性评估进行了一定研究。

上述工作大多是在试验台上进行,试验时间和成本较高,且对于性能退化的电主轴在机可靠性加速试验还缺乏研究。为此,笔者针对可靠性试验过程中的电主轴性能退化数据进行采集和分析,克服以往试验时间长、失效数据量少的困难,利用在机试验节约试验成本,并利用韦布尔分布对同类型电主轴的可靠性进行评估,验证在机电主轴可靠性评估方法的有效性。

2 电主轴性能退化量选取

电主轴性能退化的主要表现形式有电主轴精度超标、电主轴振动、异响、轴承温度升高、电主轴功率增大等,其中,电主轴的精度保持性直接影响零件的加工质量,是决定机床性能的重要指标。

笔者的试验对象为轿车动力总成加工中心的电主轴,工作特点是转速快、受力复杂。电主轴在加工过程中主要受扭矩、弯矩、不规则径向力、轴向力等切削载荷作用,在长时间切削累积载荷影响下,会出现电主轴轴承组磨损、点蚀等疲劳损坏,切削加工过程中的冲击会造成轴承组、转子等配合松动,这些影响最终会导致电主轴在高速旋转过程中稳定性变差,径向跳动增大,加工零件质量超差,以及振动、异响超标等。切削载荷对电主轴电机的影响主要表现在电主轴功率增大、电主轴加速时间变长、定子线圈工作温度上升等方面。电主轴性能退化通常都是渐变的过程,呈现出一定的变化规律。

在电主轴性能退化量的选取上,要满足以下两个条件:所选择的退化量基于电主轴失效机理分析,能够随着电主轴性能的退化一起渐变;所选取的性能退化量应该具有明确的定义。通过对电主轴性能退化机理分析,发现电主轴的性能退化大多表现为电主轴精度、振动、负载电流及温度变化,最终选择电主轴前端径向跳动、电主轴前后端轴承振动信号作为性能退化量。

3 数据采集

数据采集系统应该满足以下条件:① 可以设定性能退化数据采集的试验条件,如转速、刀具、加载量等,保证试验过程的一致性;② 多种性能退化数据同步采集;③ 自动触发数据采集、标记和保存;④ 传感器布置方便,且安装稳定。

电主轴传感器位置布置如图1所示,电主轴性能退化数据采集和处理流程如图2所示。电主轴的振动、径向跳动、负载电流等性能退化量数据采集要在相同条件下进行,即电主轴转速、夹载刀具类型、进给速度等加工工况要前后一致。在电主轴可靠性加速试验中,采集加载过程中电主轴运转比较稳定阶段的数据,减小信号受到的干扰。对电主轴性能退化量数据进行处理后,预测出电主轴性能失效时间。

▲图1 电主轴传感器位置布置▲图2 电主轴性能退化数据采集和处理流程

4 数据处理方法

采集径向跳动和电主轴前后轴承振动信号,对电主轴的性能退化进行评估预测。径向跳动和加载试验初始径向跳动之比称为径向跳动比,其阈值设定为Trout。当径向跳动比大于阈值时,即认为电主轴出现性能失效,记一次故障。对于振动信号,采用一种小波包能量偏移算法来评估退化趋势,能量偏移度阈值设定为Tes。当能量偏移度大于设定阈值时,即认为出现性能失效。

能量偏移度计算方法如下:通过小波包进行j层分解,得到2j=M个频域段,能量值Ei为:

(1)

原始信号能量值Er为:

(2)

归一化处理后得到振动信号的特征向量T为:

(3)

假设电主轴初始状态振动信号的能量特征向量为[p1,p2,…,pM],在机试验过程中电主轴前后轴承处振动信号的特征向量为[f1,f2,…,fM],则电主轴能量偏移度λ为:

(4)

基于上述算法对电主轴加速加载试验得到的数据进行处理,得到电主轴能量偏移度。对计算得到的电主轴能量偏移度和径向跳动变动率数据进行线性拟合,得到电主轴性能退化趋势,根据设置的失效阈值预测电主轴性能失效时间。

根据电主轴在机可靠性加速试验采集到的性能退化数据,得到电主轴三个性能退化量的特征退化趋势,如图3所示,回归方程列于图中。

根据技术要求,试验中阈值Trout设定为1.6,Tes设定为0.3。在生产中,普遍认为径向跳动比达到1.6表征电主轴性能出现严重退化,能量偏移度达到0.3表征电主轴已经出现点蚀、裂纹等严重故障。对应径向跳动、前后轴承振动退化量拟合结果,得到加速试验条件下电主轴性能失效时间分别为536 h、751 h、570 h,选择最短的性能失效时间536 h,作为电主轴可靠性加速试验出现性能失效的时间。在此基础上,通过确定电主轴可靠性加速试验加速因数,计算正常工况下电主轴的等效失效时间。

设加速因数为k,有如下关系式:

TN=kTA

(5)

式中:TA和TN分别为加速和正常载荷谱下加载时间。

根据逆幂律定律和疲劳累积损伤原理[13],可得:

(6)

式中:[SA]为加速试验单位时间内在载荷PA作用下电主轴受到的损伤;[SN]为正常使用情况下单位时间内在载荷PN作用下电主轴受到的损伤;me为载荷对损伤的影响因子。

根据疲劳累积损伤原理,在载荷的作用下,电主轴受到的疲劳损伤是不断累加的,各个载荷彼此之间不产生影响,当载荷累加到临界值时,就会产生疲劳损坏。

电主轴在一定载荷谱循环时间段内,加速和正常载荷谱下产生的总损伤SA、SN分别为:

(7)

(8)

对照载荷谱,进行归一化处理后得到当量累积损伤[SA]和[SN],即在单位时间内按照试验载荷谱和实际载荷谱加载所产生的损伤:

(9)

(10)

式中:Pn为额定载荷。

根据累积损伤原理,两种载荷谱造成的损伤一致,于是有:

▲图3 电主轴性能退化量特征退化趋势

[SA]TA=[SN]TN

(11)

进而可得:

TN=[SA]/[SN]=kTA

(12)

载荷谱等级划分规则如下:0～3%额定载荷为空载,3%～30%额定载荷为轻载,30%～70%额定载荷为中载,70%～100%额定载荷为重载。按照划分规则对机床实际加工过程受到的载荷进行划分,得到机床实际载荷谱。

机床加速试验载荷谱如图4所示,实际生产载荷谱计算得到加速因数k为10.56。加速试验下根据性能退化量预测电主轴性能失效时间为5 660 h。

5 电主轴可靠性评估

通过实际收集到的同类型电主轴性能故障数据计算可靠性指标,与所预测的电主轴性能失效时间进行对比。

大量研究发现,机械产品的故障间隔时间服从两参数韦布尔分布。累积分布函数F(t)为:

▲图4 机床加速试验载荷谱▲图5 机床实际生产载荷谱

(13)

式中:m为形状参数;η为尺度参数;t为故障时间。

概率密度函数f(t)为:

(14)

可靠度函数R(t)为:

(15)

电主轴平均故障间隔时间的点估计MTBF为:

(16)

因此,只要求出m和η的估计值,就可以估算出电主轴的故障间隔时间。

利用最小二乘原理来确定韦布尔分布参数,对式(13)取对数:

(17)

令:

(18)

x=lnt

(19)

A=-mlnη

(20)

B=m

(21)

依据最小二乘原理:

(22)

(23)

(24)

(25)

得到韦布尔分布的参数估计值:

(26)

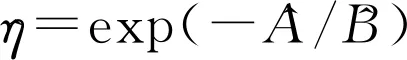
(27)

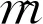
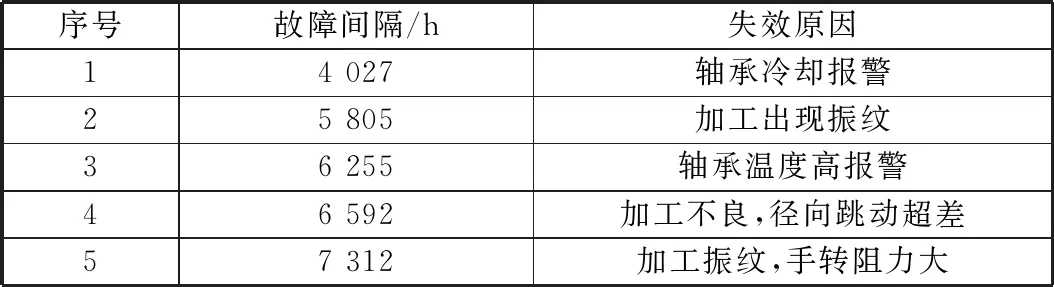
表1 同类型电主轴故障数据

6 结束语

笔者基于电主轴的性能退化量和自动化数据采集系统,提出一种电主轴在机可靠性试验和评估方法。应用这一方法,可以在电主轴使用现场进行试验,在软件中设置参数后自动实现数据采集,对电主轴出现性能故障的时间进行预测。与同类型电主轴性能故障数据跟踪统计计算的可靠性指标进行对比,两种方法得到的结果有很好的一致性,验证了在机可靠性试验和方法的有效性。这一方法还可以进一步推广应用于电主轴运行可靠性监测。