溢流前缘长度变化对直角折线堰过流能力影响研究

王尚今，邱 勇，周鑫宇，王文兵，王靖超

(云南农业大学水利学院，云南 昆明 650201)

随着生态工程学的兴起，董哲仁等人[1]将传统水利工程与生态学相结合，首先于2003年提出了生态水工学这一概念，确保水利工程在满足人类发展需求的同时，将其对环境的负面影响最小化，以促进人与自然和谐相处。中小型生态河道的治理，越来越注重其自身所具有的自然景观，在使河道中的挡水建筑物体现生态效果的同时，也要保证河道的防洪安全。直角折线堰作为一种堰型独特的亲水设施，不仅有着优美的溢流景观，能够很好的与周围环境融为一体，而且能在河道宽度不变的情况下增加溢流前缘长度，从而增大过流能力。

通过检索，文献[2]借助能量方程推求双曲线型薄壁堰流量的基本计算公式，给出流量与堰顶水头的比例关系；文献[3]应用相关性分析、线性回归方法，整理推导出Ⅱ型折线型实用堰流量系数计算方法；文献[4]和[5]研究了堰高一定，前堰与侧堰相等，且在同时减小情况下Z形薄壁堰的流量系数估算公式。文献[6]基于堰流基本计算公式对侧堰位置不变，只改变侧堰长度的直角折线堰，拟合得到了流量系数计算公式；文献[7]针对侧堰长度不变，改变其位置的直角折线堰，拟合得到了过流能力。上述文献均将过流宽度默认为河道宽度。但通过水工模型试验研究发现，直角折线堰的过流能力和溢流前缘长度变化直接相关。

1 试验方案及布置

结合河道地形条件要求，直角折线堰平面布置形态如图1所示，由前堰、侧堰和后堰组成，河道宽度w为150mm，上下游堰高P均为100mm，堰宽d为10mm，前堰长度a分别为37.5、75.0、112.5mm，侧堰长度b分别为75.0、112.5、150.0mm，后堰长度c分别为112.5、75.0、37.5，展长B=a+b+c。将不同体型进行组合，一共得到9组试验方案。不同试验方案体型尺寸见表1。

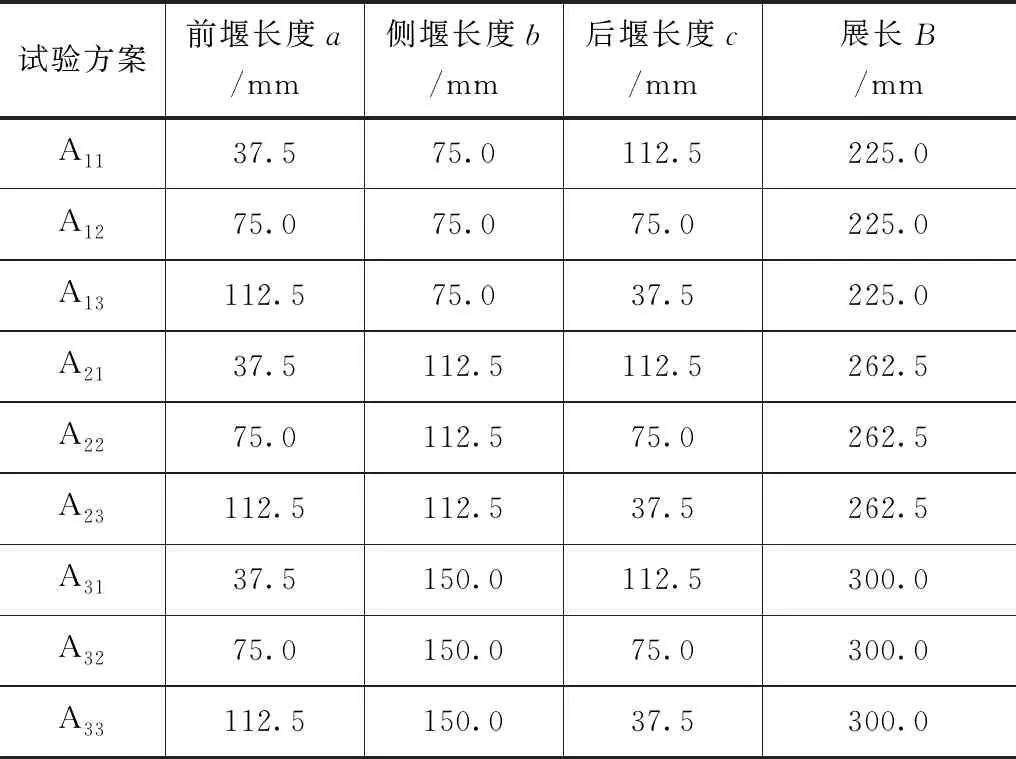
表1 直角折线堰不同试验方案体型尺寸

图1 直角折线堰平面布置示意图

2 试验成果及分析

2.1 试验成果

通过水工模型试验，对直角折线堰进行测试，得到不同方案下的过流能力，将之与文献[8]成果中相同堰宽、相同堰高的WES实用堰过流能力作比较，见表2。

由表2可知，在小流量情况下，直角折线堰的过流能力均大于WES实用堰，当堰顶水头超过1.4倍堰高时，过流能力开始小于WES实用堰。

随着前堰长度的增加，直角折线堰过流能力呈现先增大后减小的趋势；而侧堰长度增加，直角折线堰过流能力虽然不断增大，但增幅逐渐减小。此外，还可以发现，不管是侧堰位置变化(前堰长度增加)，还是侧堰长度增加，都会出现侧堰和后堰之间的来流供给不足，从而导致侧堰和后堰过流能力出现不同程度的下降，进而影响直角折线堰过流。

2.2 过流流态

观察直角折线堰过堰水流流态，相同流量情况下，随前堰长度增加(改变侧堰位置，但维持其长度不变)，后堰堰顶水头小于前堰情况趋于明显；另外，受侧堰与后堰之间空间变化影响(后堰长度逐渐减小)，侧堰堰顶水头沿水流方向减小加剧。

相同流量情况下，前堰长度不变(固定侧堰位置)，随侧堰长度增加，直角折线堰的溢流前缘长度相应增加，但受侧堰与后堰之间空间制约，后堰堰顶水头反而下降，侧堰过堰水流流线和侧堰夹角变小。

前堰长度(侧堰位置)和侧堰长度均发生变化，在低水头条件下，包括前堰、侧堰和后堰的溢流前缘长度范围内均呈薄壁堰流特征；但随着流量增大，后堰堰顶水头低于前堰，侧堰过堰水流流线和侧堰夹角由正交逐渐变为斜交，并且受前堰与侧堰之间空间水流顶托影响加大；流量继续增大，直角折线堰过流几乎呈现为前堰和后堰两个位置不同的WES真空实用堰流(此时的侧堰过流已不明显，并且沿水流方向在后堰附近出现局部壅水现象)。

3 公式拟合及验证

3.1 溢流前缘长度

由此可得，直角折线堰流的过流形态随着堰顶水头的变化而变化，因此随着流量增加，其溢流前缘长度变化也将从薄壁堰流时的模型展长B(a+b+c)过渡到WES真空实用堰流时的河道宽度w(150mm)。

薄壁堰流量系数计算公式：

(1)

表2 直角折线堰不同试验方案与WES实用堰过流能力成果 单位：10-3m3/s

图2 不同试验方案L-H回归分析图

式中，H—堰顶水头，m；P—堰高，m。

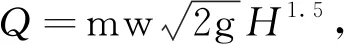
通过数学回归方法分析可知溢流前缘长度L与堰顶水深H呈指数函数关系，且均可用指数函数L=a0Hb0+c0表示，相关系数见表3。

由表3可知，不同方案下a0、b0和c0存在差异，其原因为直角折线堰溢流前缘长度不同，而溢流前缘长度随着前堰(后堰)、侧堰长度的变化而变化，即与a(c)、b有关，进而借助1stOpt软件，对参数a0、b0和c0与堰长a(c)、b进行回归分析。

为了使精度能够满足要求，采用二元三次多项式z=p1x3+p2y3+p3x2y+p4xy2+p5x2+p6y2+p7xy+p8

表3 不同试验方案L与H回归分析成果

对参数a0、b0进行拟合，得到的系数相关性均在0.96以上。

拟合得到的二元三次多项式拟合曲线方程分别为：

a0=3.448a3-5.786b3-4.032a2b+1.252ab2- 0.776a2+9.362b2-2.232ab+0.023

(2)

b0=45.971a3+21.880b3+189.630a2b+ 3.410ab2-2.047a2-2.644b2-32.000ab-0.490

(3)

c0=-71.841a3-23.580b3-10.335a2b+ 59.923ab2+14.708a2+4.166b2- 13.284ab+0.070

(4)

由此可得表3中直角折线堰溢流前缘长度L的拟合公式，在不同堰顶水头情况下的溢流前缘长度L计算值见表4。

由表4可清楚地看出，随着堰顶水头的增加，溢流前缘长度均呈现下降的趋势。但需要指出，当计算得到的溢流前缘长度小于150mm时，应将其视为过流宽度不再变化(恒为150mm)。

3.2 流量系数

根据堰流基本公式可知，流量系数与堰顶水头相关。固定过流宽度为0.15m，将直角折线堰流量系数与相应堰顶水头进行数学回归分析。当流量系数mw与堰顶水头H使用指数模型建立函数时，相关性达到0.99，见表5。

由表5可知，每个方案的系数a1、b1和c1都有差异，运用相同方法进一步拟合。当采用二元三次多项式拟合时，可得：

a1=-36.107a3+0.737b3-48.166a2b+ 8.154ab2+4.085a2-0.377b2+ 5.031ab+0.009

(5)

b1=-522.183a3-55.985b3+91.876a2b+ 113.114ab2+57.454a2+11.779b2- 30.151ab-0.784

(6)

c1=124.727a3-35.319b3-10.098a2b+ 40.059ab2-9.643a2+5.290b2- 7.813ab+0.340

(7)

亦即流量系数mw可表示为前堰a、侧堰b的函数关系式。

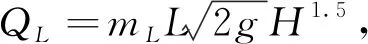
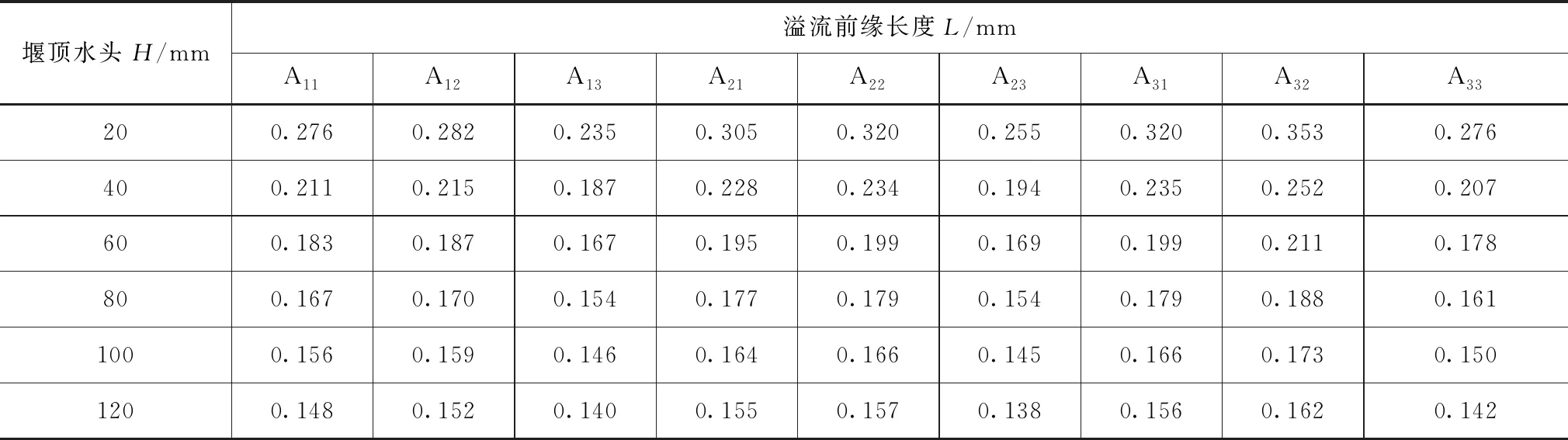
表4 不同试验方案溢流前缘长度L拟合成果

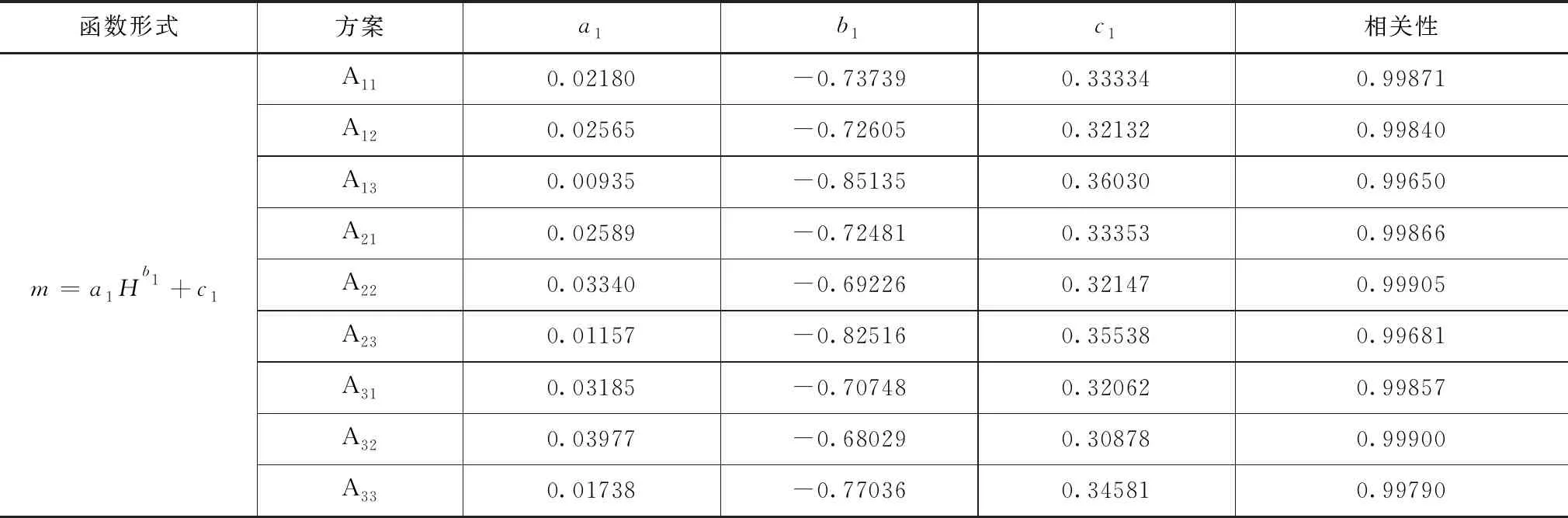
表5 不同试验方案mw与H回归分析成果

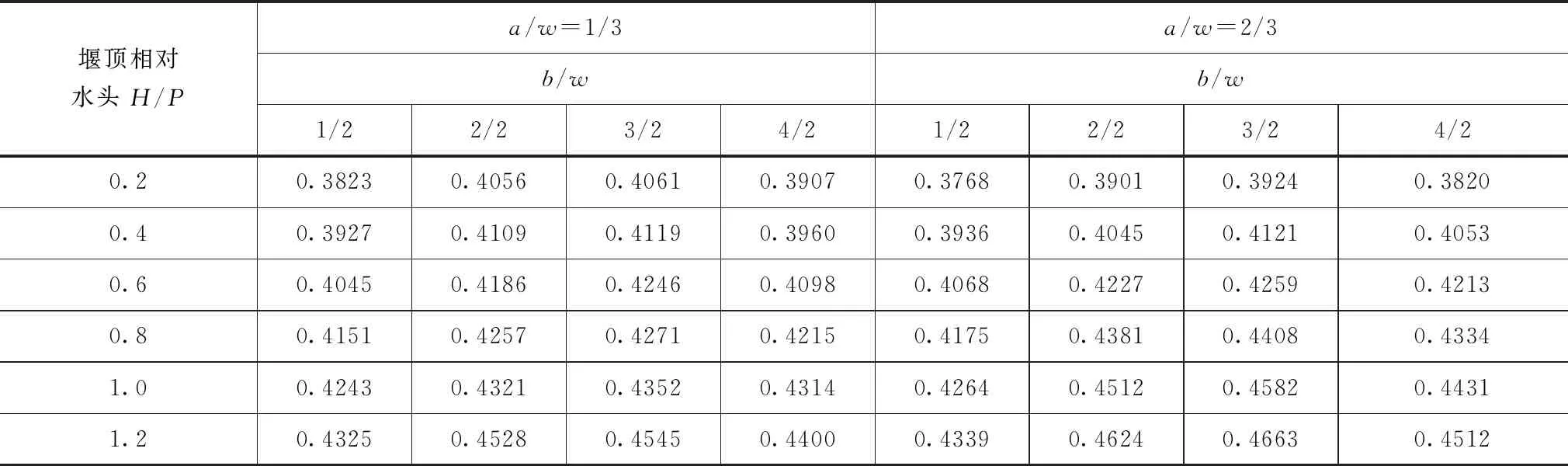
表6 不同方案流量系数mL计算成果

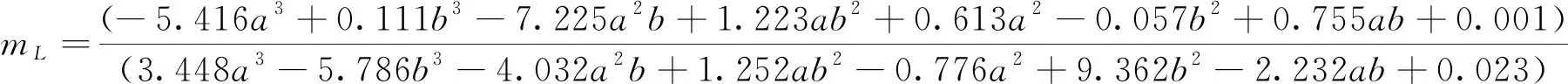
(8)

式(8)即为考虑溢流前缘长度变化影响的流量系数计算公式。

3.3 拟合公式分析

对拟合所得考虑溢流前缘长度变化下的流量系数公式(8)进行分析。

(1))侧堰长度不变(以b=0.75w为例)情况下，只改变前堰长度(亦即溢流前缘长度固定不变)，对拟合得到的公式(8)求极值：H分别为0.5、1.0、1.5倍堰高P时，a取0.073、0.076、0.077m可以使流量系数mL最大。故认为：侧堰位于河道中部位置，过流能力更容易保证。

(2)侧堰位置固定(前堰长度不变，以a=0.5w为例)，长度不断增加(亦即溢流前缘长度变化)，在一定堰顶水头(以H=P为例)条件下，分析公式(8)可以发现，b的长度从0.5倍过流宽度依次增加到0.75、1、1.25倍过流宽度时的曲线斜率变幅(过流能力增幅)分别为93.7%、86.8%和13.6%。表明侧堰长度的增加有助于过流能力的提高，但其增长幅度呈下降趋势，特别是当侧堰长度超过1.25倍过流宽度后，过流能力增加已不明显。

(3)前堰长度和侧堰长度都发生改变(亦即溢流前缘长度变化)，根据公式(8)得到的流量系数见表6。

由表6可知，直角折线堰流量系数mL随着堰顶水头的增加而增大。另外，在低水头条件下，侧堰靠近右岸时过流能力略大；随着堰顶水头增加，侧堰靠近左岸时过流能力稍大。

3.4 工程应用

按照重力相似准则，分析几何比尺λ放大后的流量系数，其值和公式(8)的计算结果存在差异，原因在于拟合参数和比尺变化有关。此时需要对前堰长度a和侧堰长度b进行比尺转换，得到基于模型变化按比尺放大后的流量系数mp计算公式。

(9)

其中：

(10)

(11)

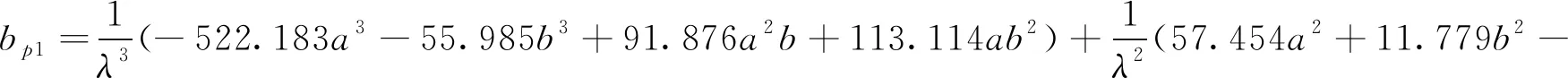
(12)

(13)

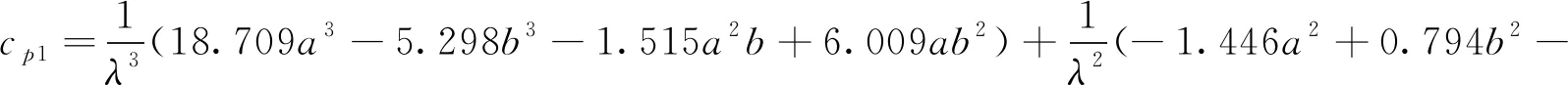
(14)

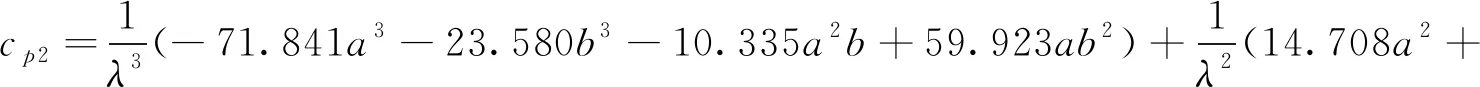
(15)

根据公式(10)—(15)可以求得经几何比尺λ放大后的各参数，代入公式(9)求得实际工程的流量系数mp，可为类似工程提供参考。

4 结语

基于不同方案的试验成果，通过拟合得到直角折线堰在溢流前缘长度变化下的流量系数计算公式。得出结论如下：

(1)侧堰长度不变，前堰长度增加(溢流前缘长度不变)，直角折线堰过流能力先增加后减小，前堰长度为河道宽度一半时过流能力达到最大。

(2)前堰长度不变，侧堰长度增加(溢流前缘长度增加)，直角折线堰过流能力持续增加，但增幅在侧堰长度达到一倍河道宽度左右后急剧减小。

(3)前堰长度和侧堰长度均发生变化(溢流前缘长度改变)，直角折线堰过流能力在前堰长度为一半河道宽度，侧堰长度接近一倍河道宽度时过流能力相对较大，且堰后流态较好，能够在保证河道行洪能力的同时具有较好的水景观。