基于Max-stable模型的淮河流域气候极值空间建模分析
2020-06-23王怀军赵卓怡潘莹萍杨雅雪
王怀军,赵卓怡,曹 蕾,潘莹萍,,冯 如,杨雅雪
(1. 淮阴师范学院城市与环境学院,江苏 淮安 223300;2. 南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏 南京 210029;3. 南京水利科学研究院水利部应对气候变化研究中心,江苏 南京 2100294;4. 北京师范大学地理学部,北京 100875)
全球气候变化,特别是极端气候事件的频率加剧,可能对人类生命、财产和生态系统的可持续发展造成严重的影响[1- 3]。全球变暖导致极端气候事件的频率、强度、空间范围和持续时间发生改变,也可能导致前所未有的极端气候事件[4]。联合国减灾办公室(UNISDR)和灾害流行病学研究中心(CRED)报告显示:1995—2015年,有33.94亿人受到与天气有关的灾害(如洪水、极端温度和干旱)的影响,更严重的是造成34.3万人死亡[5]。研究者试图利用各种方法来解释全球变暖对极端气候的影响,且多数研究侧重通过趋势分析探测极端气候的时空变化规律[6]。结果显示,世界上大部分地区暖日和暖夜呈上升趋势,冷日和冷夜呈下降趋势[7]。同时,很多研究也指出极端气候变化的不确定性远远超过平均气候变化的不确定性[8],这可能与空间数据建模以高斯过程实现有关[9]。此外,多元正态分布是为平均态而设计,其会低估极端气候的概率,因此不适用于极值数据建模[10]。
近年来,Max-stable在极值空间建模中的应用受到了相当大的关注,因为它是多元极值分布的一种自然扩展[11]。Max-stable模型在极端降水[12]和极端温度[13]已有报道,结果均表明该模型可以很好地模拟气候极值的空间变化特征。例如,Padoan等[14]和Davis等[15]认为Max-stable可以描述极值数据的空间结构和特征。Lee等[16]开发了一个通用的Max-stable模型,并演示了该模型在韩国年最高温度变化的模拟能力。Zhang等[17]表明降水极值的空间分布受地形影响,增加海拔作为协变量可以提高Max-stable模型的估计精度。
淮河流域位于中国南北向气候过渡带,是中国南水北调工程实施的重要区域。近几十年来,该地区极端降水的频率和强度呈上升趋势[18]。以往的研究大部分关注极端降水的概率分布特征。例如,She等[19]和Zheng等[20]观察到,月降水量更适合于广义帕累托分布。然而很少有研究考虑数据的空间相关性。由于极值空间分布和气候变化风险是高度相关的,也是评估气候变化背景下极值对环境危害影响的前提[21]。在这项研究中,我们研究了1日最大降水量(RX1day)和年最高气温(TXx)的Max-stable过程,以期通过选择最优空间极值模型来表征极端气候的空间变化规律。
1 研究区域、数据和方法
1.1 研究区域和数据
淮河流域占地27万km2,位于长江流域和黄河流域之间。淮河流域位于我国南北气候过渡地带,北起暖温带气候,南至亚热带气候;年平均气温11~16℃;月平均最高气温发生在7月,约为25℃,月平均最低气温发生在1月,约为0℃,最高气温达44.5℃。降水发生在6月至9月,年平均降水量约为920mm,一般由南向北、由山地向平原、由海岸向内陆递减。
淮河流域1960—2018年34个气象站日值气温和降水数据来自中国气象数据服务中心(http://data.cma.cn/en)。东亚夏季风指数(EASM)来自http://ljp.gcess.cn/dctpage65577。气候极值指数采用RClimDex软件计算,其可以得到11个极端降水类指数和16个极端温度类指数。本研究选择RX1day和TXx分别为1日最大降水量和年极端最高气温。纬度、经度、海拔和国内生产总值(GDP)被视为Max-stable模型的空间协变量;纬度、经度、海拔、GDP变化范围分别为30.73°N-36.75°N、11.5°E-121.6°E、0~2160m、0~53178元。
1.2 方法
极端气候事件趋势的计算采用Mann-Kendall检验[22- 23],由于该检验的结果容易受到时间序列自相关的影响,因此采用R语言包(“ZYP”)来消除lag- 1自相关的影响[24]。极端气候事件的空间变化是通过Max-stable建模过程来计算,该模型充分考虑了极端气候事件的空间相关性。Max-stable模型采用R语言包“SpatialExtremes”计算[25],计算过程如图1所示。
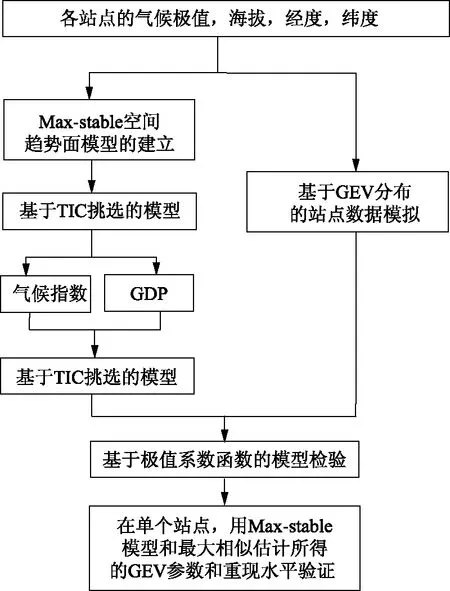
图1 模型计算过程
下面简要描述Max-stable建模过程。
随机过程Z(·)是一个独立同分布随机场(Yi(x),x∈Rd)上的最大值极限过程。如果存在常数an(x)>0、bn(x)∈R满足
(1)
那么我们就能把Z(·)视为一个Max-stable过程,在区域极端气候分析中,Z(·)可以看作是S个具有固定地理位置站点的气候极值的一个随机变量,其中用n表示时间段,一般为365天(1年)。同时,Z(·)的边际分布遵循广义极值分布(GEV):
(2)
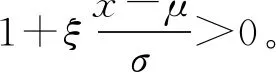
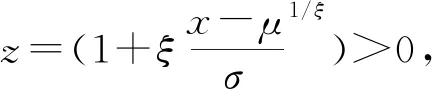
Pr[Z(x) ≤Z]=exp(-1/z),z>0
(3)
使用Brown-Resnick模型表示Max-stable过程的分布函数,其二元累积分布函数(CDF)表示如下:
Pr{Z(x1≤Z1,x1≤Z1)}=exp[-1/z1Φ(a/2+
1/alog(z2/z1))- 1/z2Φ(a/2+1/alog(z1/z2))]
(4)
式中,a=Var{Y(x1-x2)},Y(·)是稳定Gaussian过程;Φ—标准正态累计分布函数。
空间极值的相关性可以用极值系数(extremal coefficient)来表示,两点之间的极值系数表示如下:
(5)
式中,γ—半变异方差;h—两个地点之间的欧几里得距离;极值系数的值在[1,2]中变化,1—完全相关,2—完全独立。
由于传统的似然方法需要对所有站点求取密度函数,因此不能直接用于Max-stable模型,研究采用成对似然法拟合Max-stable模型。
在考虑没有观测数据地区的空间极值时,可以将纬度、经度和海拔的属性数据视为GEV分布的协变量。本研究建立了16个以经纬度为协变量的Max-stable模型,见表1。采用Takeuchi信息准则(TIC)从以上模型中确定最佳拟合模型,TIC最小的模型确定为最佳拟合模型。然后,在最佳拟合模型中加入海拔、GDP和气候指数,分析这些指数是否降低TIC值。如果TIC值降低,这些指标将被认为是Max-stable模型的协变量。重现水平计算如下:
(6)
式中,μ、σ、ξ—位置,尺度和形状参数,yT—T年重现水平。
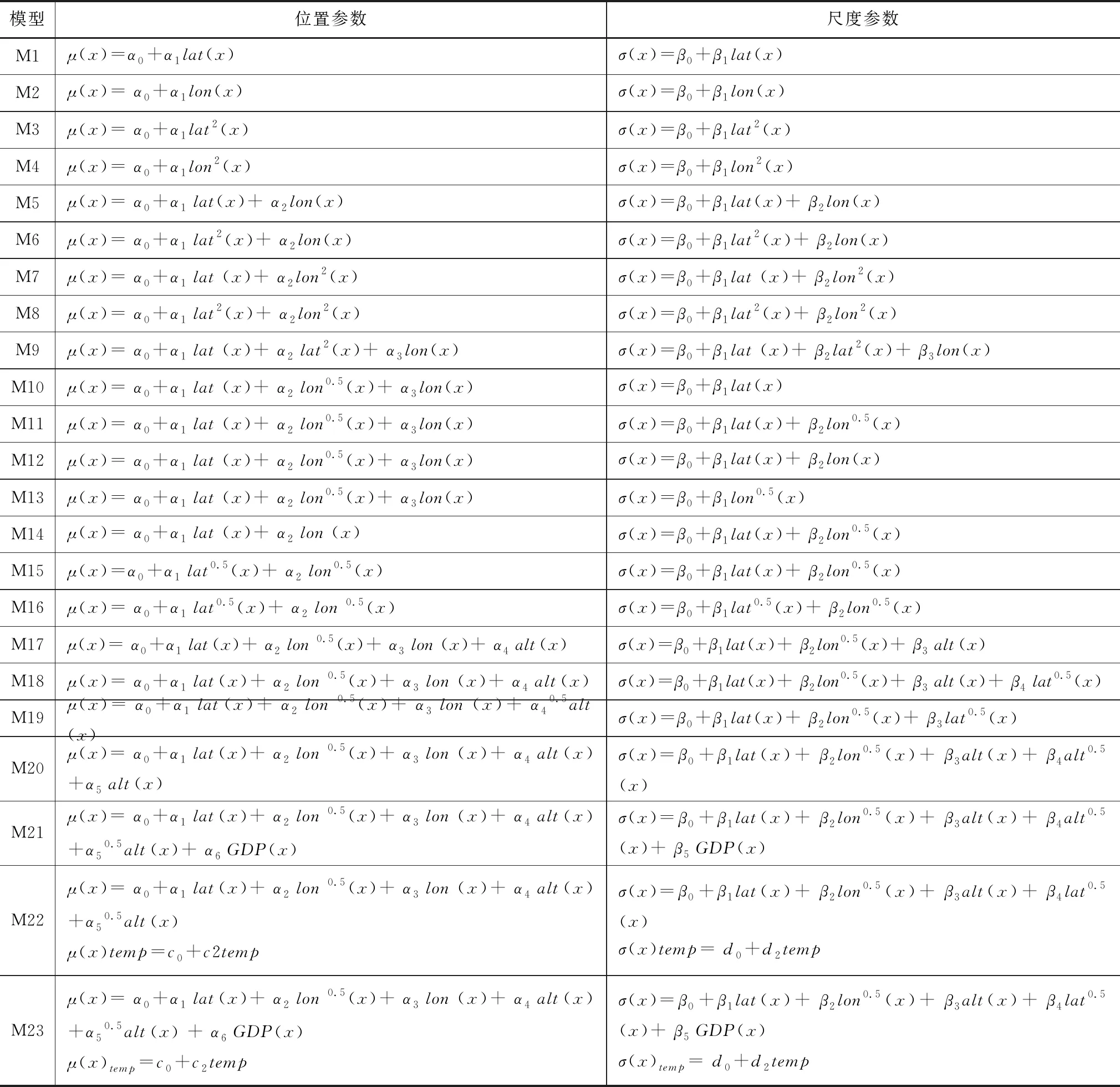
表1 广义极值分布参数协变量模型
注:lon(x)和lat(x)分别是x站的经度和纬度;alt(x)、GDP(x)分别是x站的高程和国内生产总值;temp表示时间协变量;μ、σ分别表示位置和尺度参数。
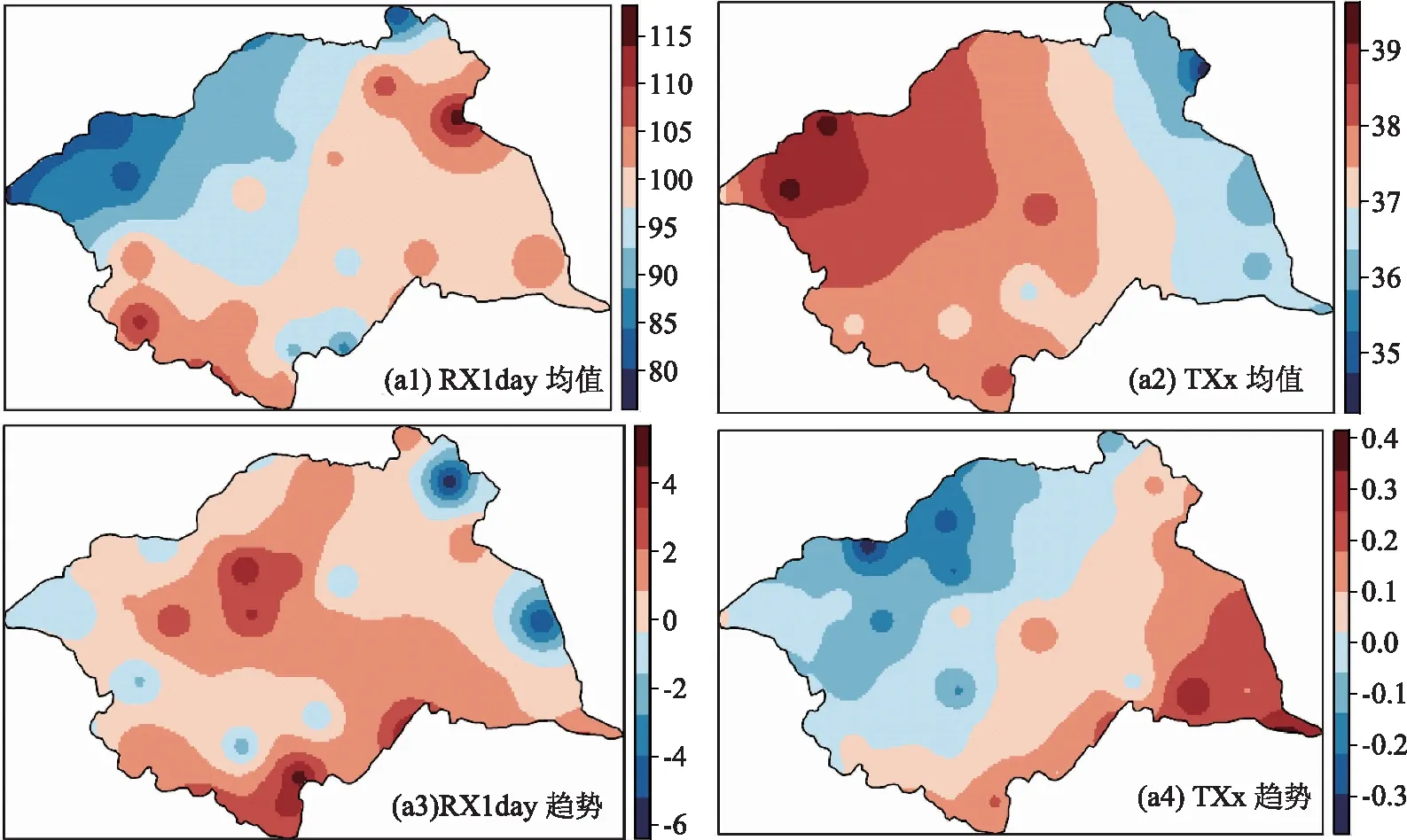
图2 中国淮河流域气候极值平均值和趋势强度
2 结果和分析
2.1 气候极值空间变化
图2展示了淮河流域气候极值的空间均值和趋势。TXx在35~39℃之间,且由东向西递增,这是由于陆地升温的速度比海洋快,离海岸越近,海洋对它的影响就越大。TXx趋势为流域东南部呈上升趋势,西北部呈下降趋势。RX1day的均值范围为80~115mm。由于受海洋和东亚季风的影响,较西北地区而言,流域东南部的RX1day显示出相对更高的值。RX1day的空间趋势为-4~4mm/10年,但无显著空间趋势分布。TXx和RX1day均呈上升趋势(TXx为0.02℃/10年,RX1day为0.55mm/10年),但只有TXx在0.05显著水平上显著。
2.2 气候极值空间建模
运用单变量GEV模型对TXx和RX1day时间序列进行拟合,并与环境参数进行相关关系分析,见表2。对于TXx的位置参数,经度相关系数为-0.67,说明TXx的空间分布与经度密切相关,与图2a2的空间分布趋势具有一致性。此外,尺度参数与经度之间也存在负相关关系,表明在经度数值大的地方方差较小。与此相反,纬度与尺度参数呈现正相关系数,说明TXx在高纬度地区具有较高的方差。对于RX1day,位置参数与纬度/经度之间的关系为负/正系数,表明高RX1day发生在低纬度、高经度,这与图2a1的结果近似。此外,RX1day的均值和方差随着海拔的降低而增加。因此,可以推测经度、纬度和海拔等变量可能影响淮河流域极端气候事件的空间分布。
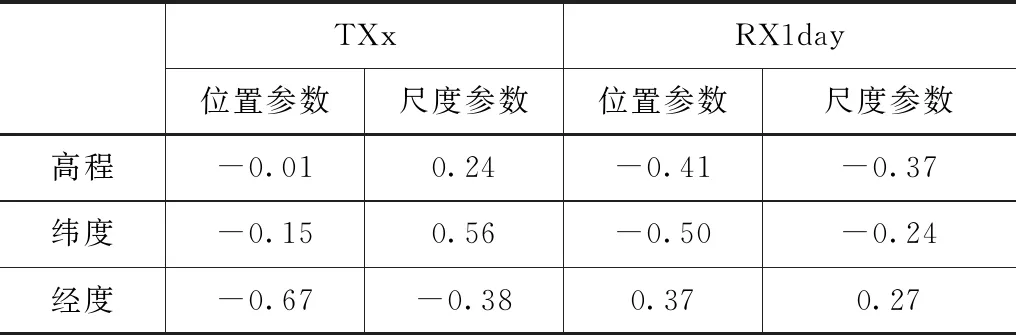
表2 站点GEV分布所得位置、尺度参数与海拔、纬度、经度相关关系
为进一步研究经纬度对极端气候事件的影响,以经度和纬度作为Max-stable模型的协变量建立模型,选择TIC值最低的模型为最佳模型,如3所示。M11是TXx和RX1day的最佳模型。将海拔加入到M11得到模型M17-M20中(表1),结果显示TIC值下降,说明海拔提高了模型模拟性能。除了经度、纬度、海拔等因素外,人类活动等其他因素也可能影响极端气候事件的空间格局。此外,由于许多气候时间序列是非平稳的,加入非平稳性的Max-stable模型可能比单一极值建模更为可靠[11]。因此,论文还关注了具有这些协变量(例如,反映人类活动的GDP和气候指数)的Max-stable模型(表1)。从图3可以看出,TXx加入GDP后(M21)TIC下降,而RX1day的TIC保持稳定。夏季EASM作为GEV参数的时间协变量加入到Max-stable模型后,TIC值并没有降低,表明添加时间协变量并不能提高模型的性能。因此,TXx选择有TIC最低值9756的M21作为最佳模型,而RX1day选择有TIC最低值26252的M20作为最佳模型,如图3a、3b所示,见表3。
图4展示了基于最优Max-stable模型得到极值系数(TXx采用M21,RX1day采用M20)估计对(θ)的距离(h)散点图。理论极值系数函数(用红线表示)也表明所选择的Max-stable模型适用于极端气候事件的空间建模。除此之外,单个站点GEV分布和Max-stable模型估算的位置和尺度参数具有高度相关关系,特别是TXx,M20位置和尺度参数的决定系数分别达到0.66和0.32。TXxM21尺度参数的决定系数相比M20(0.32)增加到0.43,如图5所示,说明人类活动确实影响了TXx的空间格局。此外,我们还评估了单站点GEV重现水平和Max-stable模型重现水平在观测站点的相关关系,见表4,所有决定系数均在0.05显著水平上显著。当然,我们还注意到,当TXx考虑GDP时,不同重现水平的决定系数均有所增加,而RX1day的决定系数未增加。这说明Max-stable模型能够准确模拟空间极值,而GDP这一协变量的添加提高了淮河流域TXx模拟的性能。
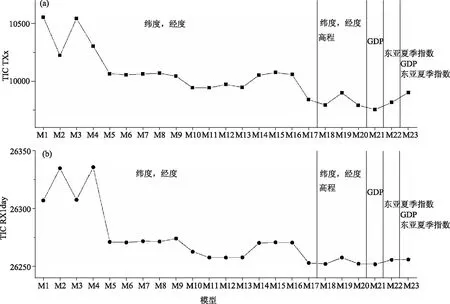
图3 不同Max-stable模型下TXx和RX1day的TIC值散点图
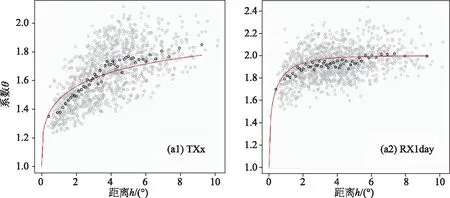
图4 基于半变异函数的TXx和RX1day拟合极值系数随距离变化图
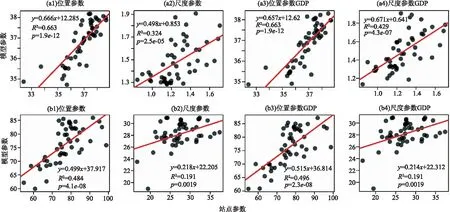
图5 各站点TXx(a1-a4)和RX1day(b1-b4)Max-stable模型估计的GEV参数与最大似然估计估算的站点GEV参数关系散点图

位置尺度TICM20(TXx)μ(x)=-1236.36-3.01 lat(x)-10.93 lon (x) +226.80lon 0.5(x) -0.0045 alt(x)+34.2 alt0.5 (x)σ(x)=66.62+2.01lat(x)+0.05lon0.5(x)+ 0.0003alt(x)-22.82alt0.5(x)9794M21(TXx)μ(x)=-1353.87-3.82 lat(x)-11.73 lon (x) +244.12lon 0.5(x) -0.0036 alt(x)+43.14 alt0.5 (x)+0.31GDPσ(x)=66.32+1.89lat(x)-0.49lon0.5(x)+ 0.0002alt(x)-20.66alt0.5(x)+0.12 GDP9756M20(RX1day)μ(x)=-22877.40-30.47 lat(x)-187.46lon (x) +4074.87lon 0.5(x) -0.0035 alt(x)+317.82 alt0.5 (x)σ(x)=891.95+25.55lat(x)+3.77lon0.5(x)-0.0116alt(x)-304.06alt0.5(x)26252M21(RX1day)μ(x)=-21585.65-22.10 lat(x)-178.67 lon (x) +3886.38lon 0.5(x) -0.0079 alt(x)+221.17 alt0.5 (x)-1.85GDPσ(x)=912.23+26.17lat(x)+3.59lon0.5(x)+ 0.0114alt(x)-310.87alt0.5(x)+0.084 GDP26252

表4 站点GEV重现水平与Max-stable模型对应的站点模拟重现水平之间关系
2.3 气候极值重现水平估计
利用选择的最佳模型M20和M21计算Rx1day和TXx重现水平(2年、10年、50年和100年)的空间分布,如图6—7所示。图6b1—b4表明,TXx在考虑GDP后,大致空间分布没有变化,但总体空间格局变得不平滑;图6a1—b4表明以西北地区为代表的GDP低值地区重现水平出现下降。且观测到的重现水平与模拟的重现水平平均绝对误差空间差异更小,如图8a1—b4所示,说明加入GDP后能够更好地模拟TXx的空间格局。TXx 2年重现期的重现水平36 ~ 39℃,100年重现期的重现水平增长到39~43℃。不同重现期下的重现水平空间格局相似,东部为高温地区,西部为低温地区。这一结果表明,TXx主要表现为经向分布,其空间格局主要由经度决定。对于RX1day,当考虑GDP时,空间平均绝对误差MAE并没有变小,如图8c1—d4所示,这表明人类活动对极端降水的影响较小。10年、50年和100年重现期的重现水平空间分布与2年重现期相似,都由西北向东南递增,这个结果可以用经纬度的综合效应来解释。低纬度和高经度地区易出现高RX1day值。由于淮河流域中气象站数量较少,且气象站之间的海拔差异较小,因此尽管将海拔纳入了计算模型,研究中中海拔对极端气候事件的空间格局的影响并不显著。
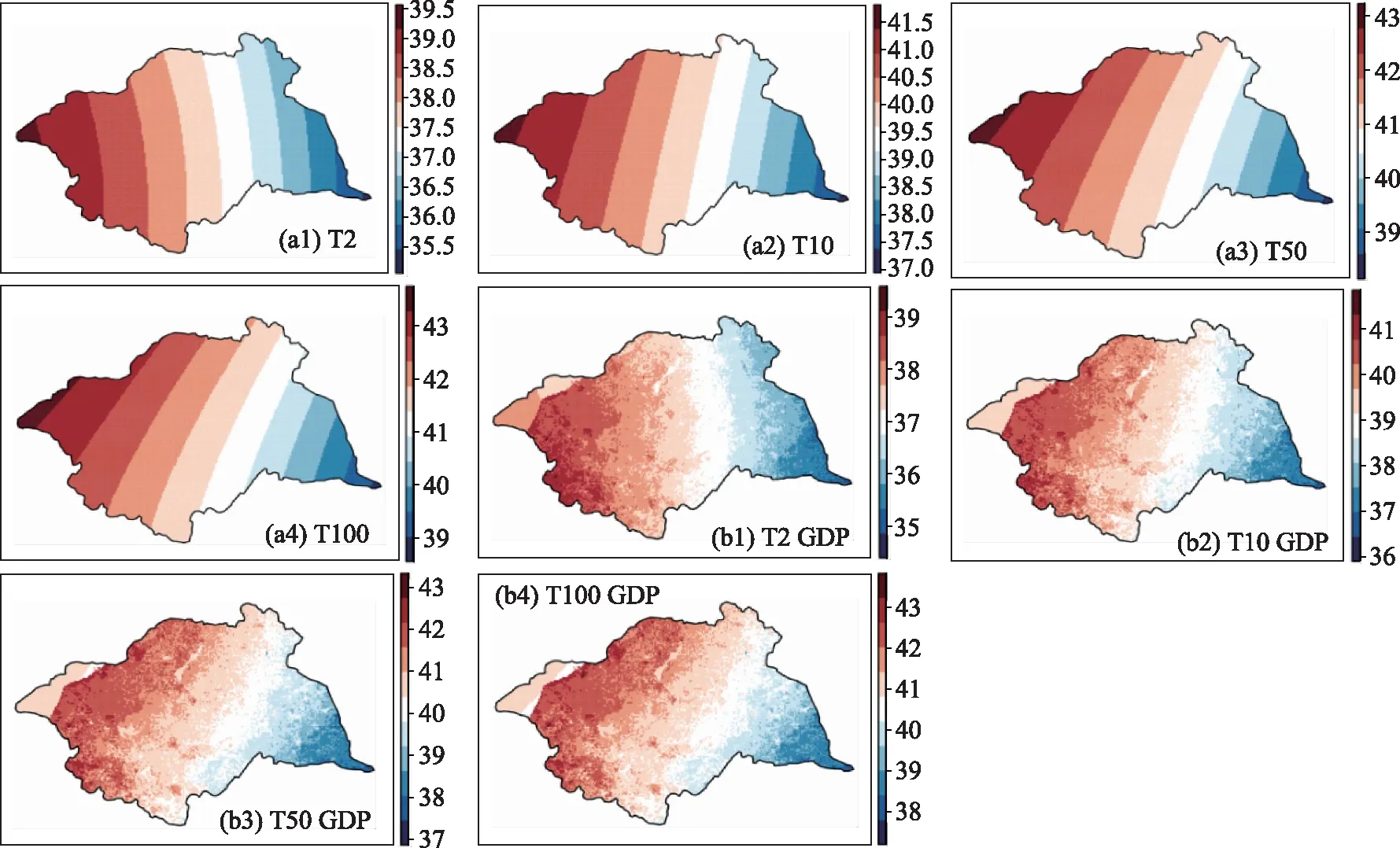
图6 TXx最佳Max-stable模型下的2、10、50和100年重现期重现水平空间分布(单位:℃)
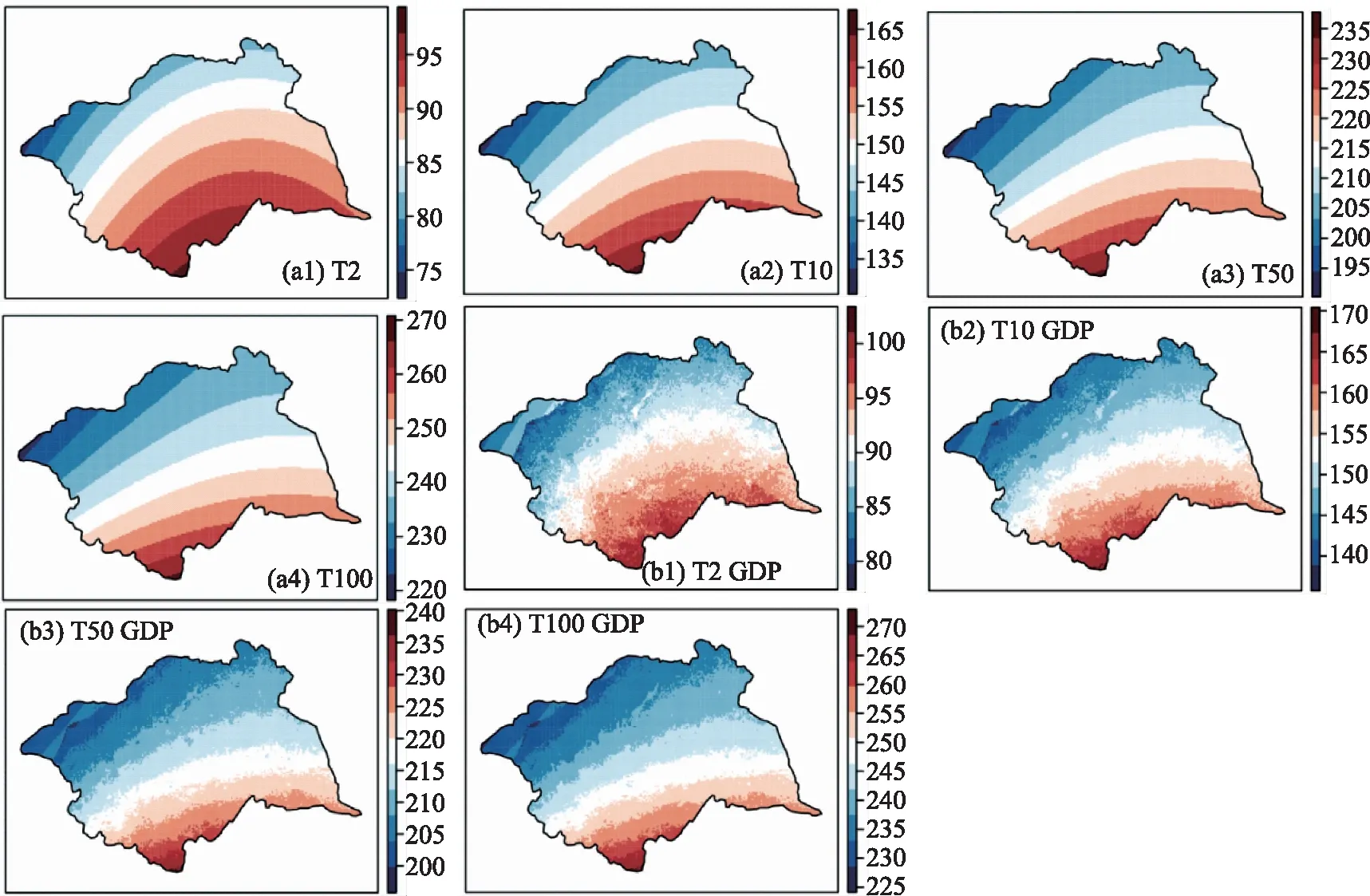
图7 RX1day最佳Max-stable模型下的2、10、50和100年重现期重现水平空间分布(单位:mm)
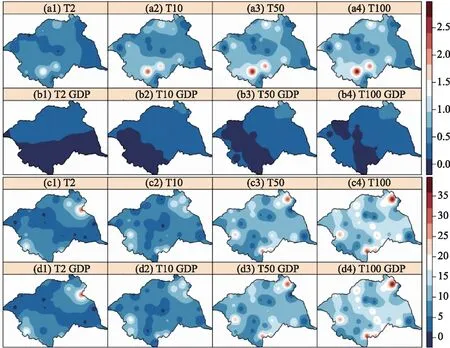
图8 TXx(a1—b4)和RX1day(c1—d4)的GEV观测数据与Max-stable模型模拟数据MAE重现水平空间差异
3 结论
本文基于Max-stable模型分析了淮河流域极端气候事件的空间分布,主要结果如下:
(1)极值系数函数、Max-stable模型模型与GEV站点相关参数散点图、平均绝对误差(MAE)图等标准表明,建立的Max-stable模型可以很好的拟合气候极值的空间变化。纬度、经度和海拔对极端气候事件的空间模拟有重要影响。GDP可以提高温度极值Max-stable模型的性能。
(2)TXx在不同重现期(2年、10年、50年和100年)下的重现水平呈经向分布,且西向东逐渐升高。此外,温度极值的空间分布也会受到以GDP为代表的人类活动的影响。RX1day由西北向东南递,这可以用经度和纬度的综合作用来解释。
由于世界上许多地方的气象数据没有监测,可以通过空间插值得到不同重现期的重现水平,其精度取决于插值方法和监测站密度。Max-stable模型的一个优点是,它可以在没有测量数据的情况下,利用海拔、经度、纬度等环境因素获取重现水平。与以往的研究相似,本文使用的Max-stable模型只能得到重现水平的空间变化,而不能得到极端气候事件的时空变化。此外,研究中使用的Max-stable模型仅适用于AM序列,而对于超门限序列(POT序列)还需要采用其它模型,如Bayesian层次模型进行空间建模。目前,我们只增加了EASM和GDP作为协变量来代表气候变化和人类活动,更多的环境变量(如离海洋距离,ENSO)将在未来的工作中进行深化。
