基于Midas/gen的高层建筑结构徐变与收缩分析
2020-06-23谢栋明王浩伟
谢栋明,王浩伟
(福建农林大学 金山学院,福州350000)
随着国内建筑结构设计、施工水平的不断提高,高层建筑结构和空间结构得到广泛应用,辅以计算机的高效运算,使高层建筑结构的施工效率、成本预算及安全稳定性上得到巨大的提升.徐变和收缩是混凝土的基本性质之一,是研究混凝土的重点方向.通过试验研究得知混凝土结构在长期荷载作用下的徐变收缩变形值可达到弹性变形的2~3倍,混凝土徐变收缩作用将导致承受长期荷载的高层建筑结构构件产生内力重分布,影响结构整体的受力情况.本文在考虑混凝土徐变收缩因素的基础上,模拟高层建筑的施工过程,将计算运行后所得数据结果进行分析,论证施工阶段的混凝土徐变收缩因素对该建筑结构的重要影响.
1 国内外高层建筑的徐变收缩研究现状
早期国内外的学者便对混凝土及其主要合成材料-水泥的收缩进行了研究,T C Powers对基于水泥含量不同的水泥石英砂浆的干燥收缩与失水的关系进行了研究[1-2];清华大学教授冯乃谦,通过实测试验对混凝土的自收缩与水灰比关系进行分析研究[3];G Bumanis等人对混凝土进行了掺入高效减水剂试验,对该情况下混凝土的徐变收缩影响进行分析[4];邓昌平等人分析了高效减水剂对水泥混凝土的影响[5].
关于混凝土徐变理论的研究,C G Lynam提出的渗出理论、F G Thomas提出了黏性流动理论以及W H Glanville 等人建立了塑性流动理论等,而徐变的常用计算方法有叠加法、有效模量法等,现常用的荷载作用下徐变计算公式是CEB-FIP,他们通过对混凝土的试验研究,为建造高层建筑提供了宝贵的数据支撑.
2 高层建筑有限元建模
高层建筑框筒结构中的有限元分析法被称为三维杆件空间分析法[2],本文的高层结构模型是利用有限元软件Midas/gen建立的,通过定义柱、梁和板,组成外框架-核心筒模型,并对该模型进行内力分析,得到高层建筑各层结构的所有单元在各种不利荷载组合下的内力分布状况,为高层结构构件受力分析和整体安全性验算提供可靠的数据支撑.
2.1 高层建筑工程概况
该高层办公楼屋面高度为291.4 m,位于8度抗震设防地区;地上建筑层数68层,地下3层;首层层高10 m;标准层高4.2 m;塔楼平面尺寸为48.5 m×48.5 m;钢筋混凝土核心筒尺寸为26 m×26 m;20层、37层及54层为该建筑的三个结构加强层(避难层).
方案如下,圆钢管混凝土柱:φ1 500~1 000 mm,Q345B;钢筋混凝土核心筒,厚1 000~450 mm,C70;外框组合梁,400 mm×1000 mm,内含型钢H700×250×8×24;内框组合梁,500 mm×1 000 mm,内含型钢H500×250×8×22;楼面梁,H型钢梁500 mm×200 mm×20 mm×20mm;楼板,100 mm厚压型钢板组合楼板;钢梁与核心筒均铰接.
三道结构加强层是利用建筑避难层设置的,它提高了结构的侧向刚度.两层高单斜撑伸臂桁架与核心筒刚接,通过加大边框梁、控制内框梁,减小结构刚度和抗剪承载力突变,提供尽可能大的大堂空间[6-7].
2.2 Midas/gen建立高层结构模型
本文通过使用Midas/gen建立模型,设定操作环境及定义材料和截面特性,采用混凝土规范GB10(RC),钢材规范GB12(S),材料选用C70混凝土和Q345钢材;定义时间依存性材料(收缩和徐变)函数,构件理论厚度假定为1m,通过修改单元的材料时间依存性特性,程序将会根据截面尺寸自动计算构件理论厚度;定义时间依存性材料的抗压强度,设计规范选用CEB-FIP(2010),CEB-FIP是计算徐变收缩常用的模型[8].该高层建筑的地上主要结构体系包括钢筋混凝土核心筒、压型钢板组合楼板、圆钢管混凝土柱、内外框组合梁[9-10].抗侧力结构体系由外框架大支撑与钢筋混凝土核心筒共同组成的,而圆钢管混凝土柱分布于结构外侧四面.如图1所示.
高层结构的首层高为10 m,内框组合梁设置为高1 m,内含型钢,且与核心筒刚接,该层6~10 m的范围内增设要桁架,提高该层结构的侧向刚度,通过增大外框桁架和控制内框梁,减小结构抗剪承载力和刚度的突变,提供了尽可能大的首层大堂空间,缺点是其首层周边净高仅有6 m,结构加强层中设置两层高单斜撑伸臂桁架与核心筒刚接.
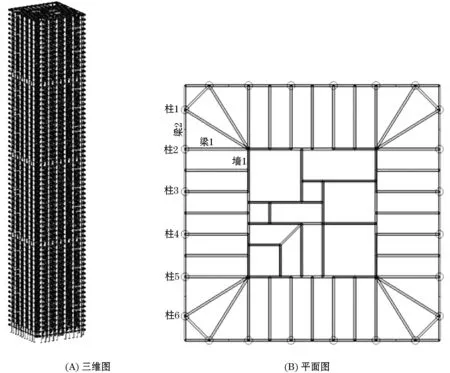
图1 高层办公楼结构示意图
3 高层建筑结构的混凝土徐变与收缩
徐变是混凝土结构在持续荷载作用下的变形随时间增长而增加的现象,对收缩的定义则是,由混凝土中物理现象(含水率变化)、化学反应及温度降低等因素引起的体积缩小[11].本文基于混凝土徐变和收缩因素的影响,模拟该高层建筑的施工过程,采用欧洲模式规范CEB-FIP(2010)的徐变与收缩计算公式,对该高层建筑的水平、竖向构件的变形进行计算分析.
3.1 混凝土徐变计算公式
混凝土的徐变系数计算公式如下:
φ(t,t0)=φ0βc(t-t0)=
φRHβ(fcm)β(t0)βc(t-t0)
(1)
(2)
(3)
其中:φ(t,t0)为加载龄期t0,计算考虑龄期t的混凝土徐变系数;φ0为名义徐变系数;βc为徐变随时间发展的系数;φRH为环境相湿度修正系数;β(fcm)为混凝土强度修正系数;β(t0)为加载龄期t0的修正系数;βc(t-t0)为徐变进程时间函数;RH为构件环境相对湿度;h为构件名义尺寸;h0取值为 100 mm;fcm为28 d 龄期混凝土平均抗压强度;fcm0为加载龄期时的混凝土抗压强度;t0为混凝土开始收缩龄期.
3.2 混凝土收缩计算公式
混凝土收缩应变计算公式如下:
εcs(t,ts)=εcs0(t,ts)βs(t,ts)
(4)
(5)
(6)
(7)
其中:t为混凝土的龄期;ts为混凝土开始收缩时的龄期;σcs(t,ts)为t时刻的收缩应变;εcs0(t,ts)为名义收缩系数;βsc由水泥品种决定,慢硬水泥取4,普通水泥和快硬水泥取5,而快硬高强水泥取8;βRH为环境相对湿度修正系数,βs(t-ts)为收缩进程时间函数;Ac为构件的横截面面积;u为与大气接触的截面周长.
4 高层结构模型的计算分析
施工方案:1)基本施工速度,标准层为7 d/层,结构加强层为15 d/层;2)框架部分施工与核心筒同步;3)将该高层办公楼分为10个施工阶段,第一个阶段是3层地下室及基础的施工,地上主体结构为68层,其施工分为8个阶段,前7个施工阶段的施工层数为9层,最后一个施工阶段的施工层数为5层,每个施工阶段63 d,其中CS3、CS5、CS6阶段71 d,地上主体完工预计为500 d.
施工阶段的恒荷载:外围框架取4.0 kN/m2,核心筒取4.3kN/m2;施工阶段的楼面施工荷载取1.0 kN/m2;施工阶段楼面的活荷载取2.0 kN/m2.
4.1 混凝土徐变收缩对框架组合梁的影响
本文将选取梁1、梁2、墙1及柱1~6构件在已定义荷载工况下的变形数据,进行高层建筑结构施工阶段与使用阶段的混凝土徐变收缩分析,构件布置详见图2(B).
选取该高层结构顶层两根框架梁进行分析,梁1为连接框架柱与核心筒的框架梁,梁2为连接外围框架柱的框架梁.截取梁1在PostCS阶段的徐变收缩荷载工况下的梁单元力图,如图1所示,梁单元端部弯矩值显示,混凝土徐变收缩对靠近剪力墙的梁端弯矩起释放作用,释放两顿约束后节点角度可以转动,梁与墙间仍保持直角不变;而对于靠近柱子一端,徐变收缩则是增大了其梁端弯矩,且该作用沿着楼层的高度的增加越发明显,这表明混凝土徐变收缩增加了梁在墙柱之间内力重分布的传力作用[12].
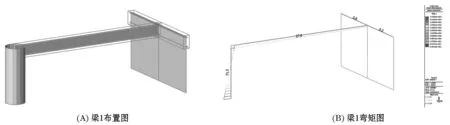
图2 梁1梁单元内力
取梁2的梁单元内力图,如图3所示,梁2的两端均为圆钢管混凝土柱,由于梁2的端部连接的是角柱1与边柱2,可以看出,混凝土徐变收缩仅对靠近柱2的梁端产生弯曲作用.而其因混凝土徐变收缩而导致梁端弯矩增加幅度,是沿着楼层高度的增加而增加.
4.2 混凝土徐变收缩对钢管混凝土柱的影响
外边框四面的钢管混凝土柱布置规则,所以仅取一面的柱进行分析,柱的变形主要是各层分配的楼面荷载所致,而由核心筒变形通过梁传递而来的弯矩较小,忽略不计.图4为柱1的最后施工阶段(CS8阶段)变形图,曲线1为柱的施工阶段弹性变形,曲线2为收缩变形,曲线3为徐变,曲线4为总变形;柱2~6最后施工阶段的变形曲线与柱1变形曲线相近,具体变形值见表1,最后的分析结果表明,混凝土徐变收缩的作用对柱的影响是随楼层高度的增加而增大的.
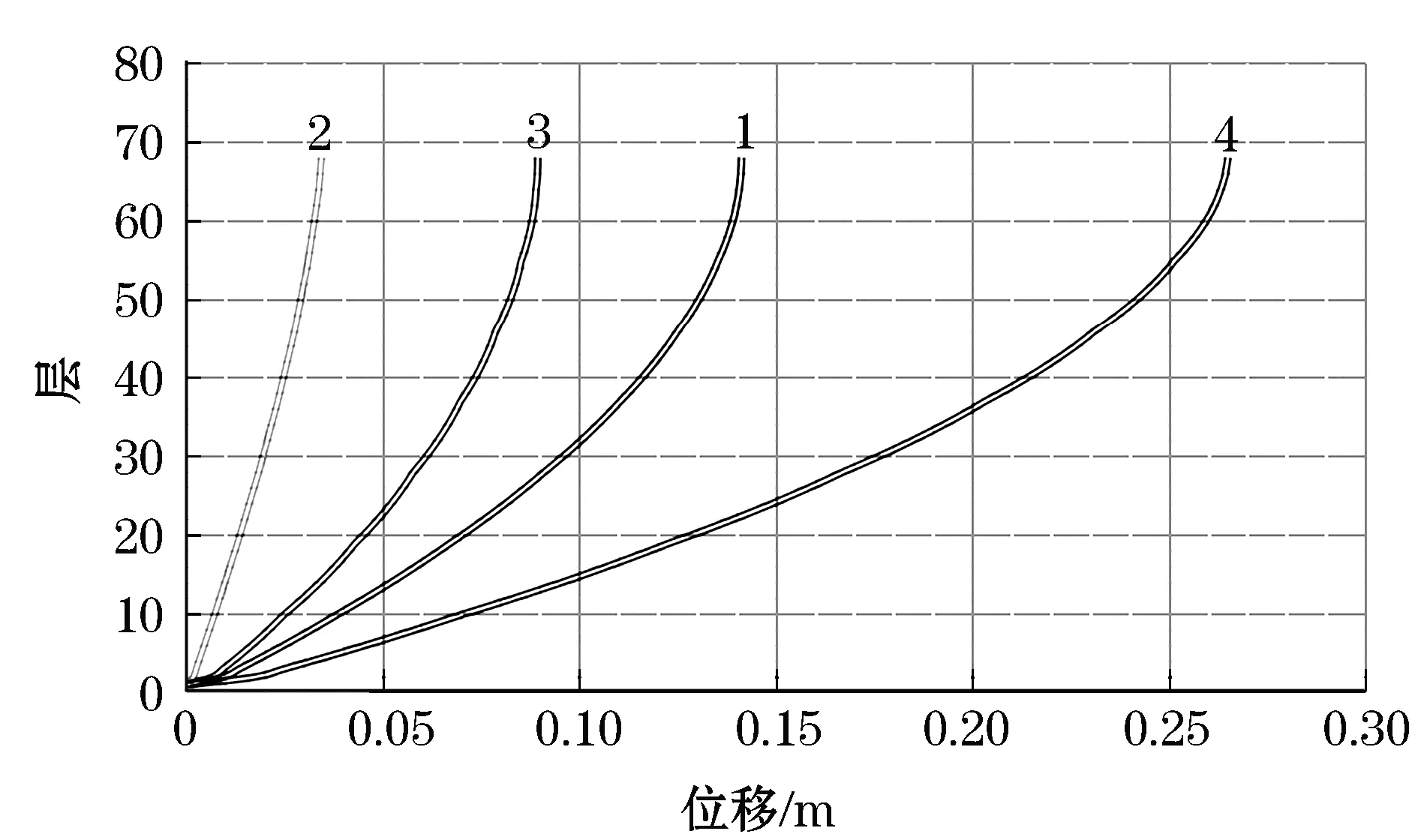
图4 柱1在CS8施工阶段的变形图
圆钢管混凝土柱的具体变形数值,以及徐变、收缩变形占总变形的比值,见表1.
表1 柱1~8于CS8施工阶段变形值及比值
表1数据显示,柱的弹性变形占总变形的53.3%,徐变变形占总变形的33.6%,而收缩变形则占总变形的13.1%,所有圆钢管混凝土柱最大的变形位置处在结构中间部位37层,其上各柱平均变形值约为260 mm;而柱顶的最大竖向位移约为25.4 mm.
4.3 剪力墙核心筒与钢管混凝土柱的竖向变形差分析
由软件运行分析结果可知,该结构的墙柱竖向变形是呈现鱼腹状的,其位移最大处在中间层(37层),所以选取柱1与墙1在首层、中间层、顶层的具体位移数值,见表2.
变形结果如表2所示,最终施工完成阶段的墙柱竖向变形差值为19 mm,由混凝土徐变收缩所引起的变形差为9 mm,占总变形差值的比例近半,对构件的影响巨大.
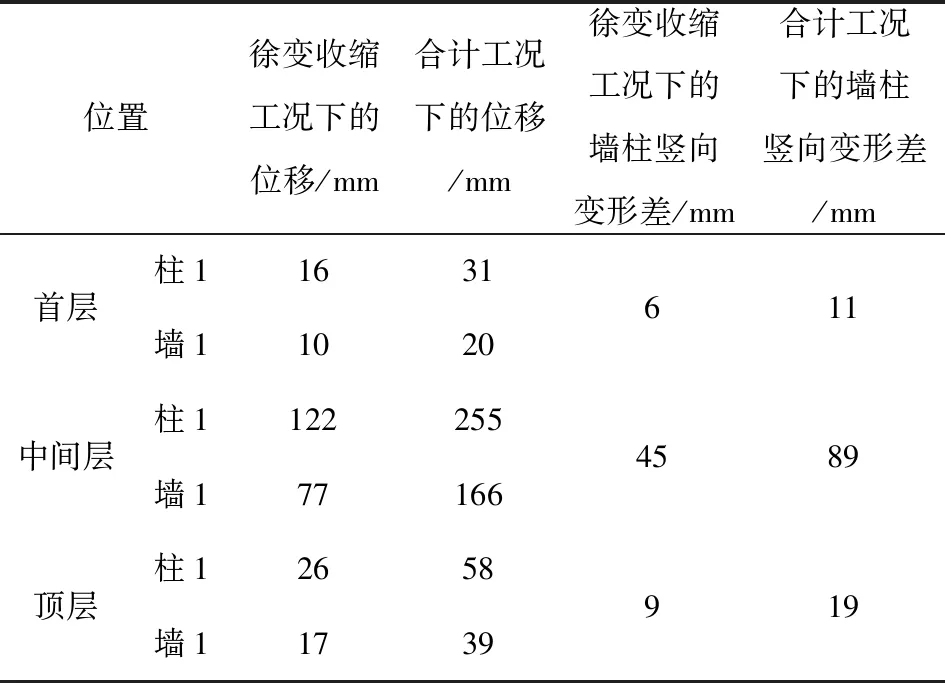
表2 不同荷载工况下不同层间的墙柱位移
选取每层柱1与墙1的位移值进行分析,如图5所示,施工阶段初期,柱1与墙1顶点部位的位移差值为0,按照施工计划进度,施工楼层数逐渐增加的同时墙、柱间的竖向变形差也将随之增加,在这种情况下有可能会导致该高层结构的墙柱构件出现裂缝,使框架梁内弯矩增加[14];应考虑外框架的梁、柱及内筒剪力墙的受力、变形等特性,加强结构框架中的薄弱部位,减少梁内弯矩[15].伸臂桁架的设置能够较好的控制墙柱间变形差,减少梁内弯矩,抑制构件出现裂缝的现象,增强了结构整体性.
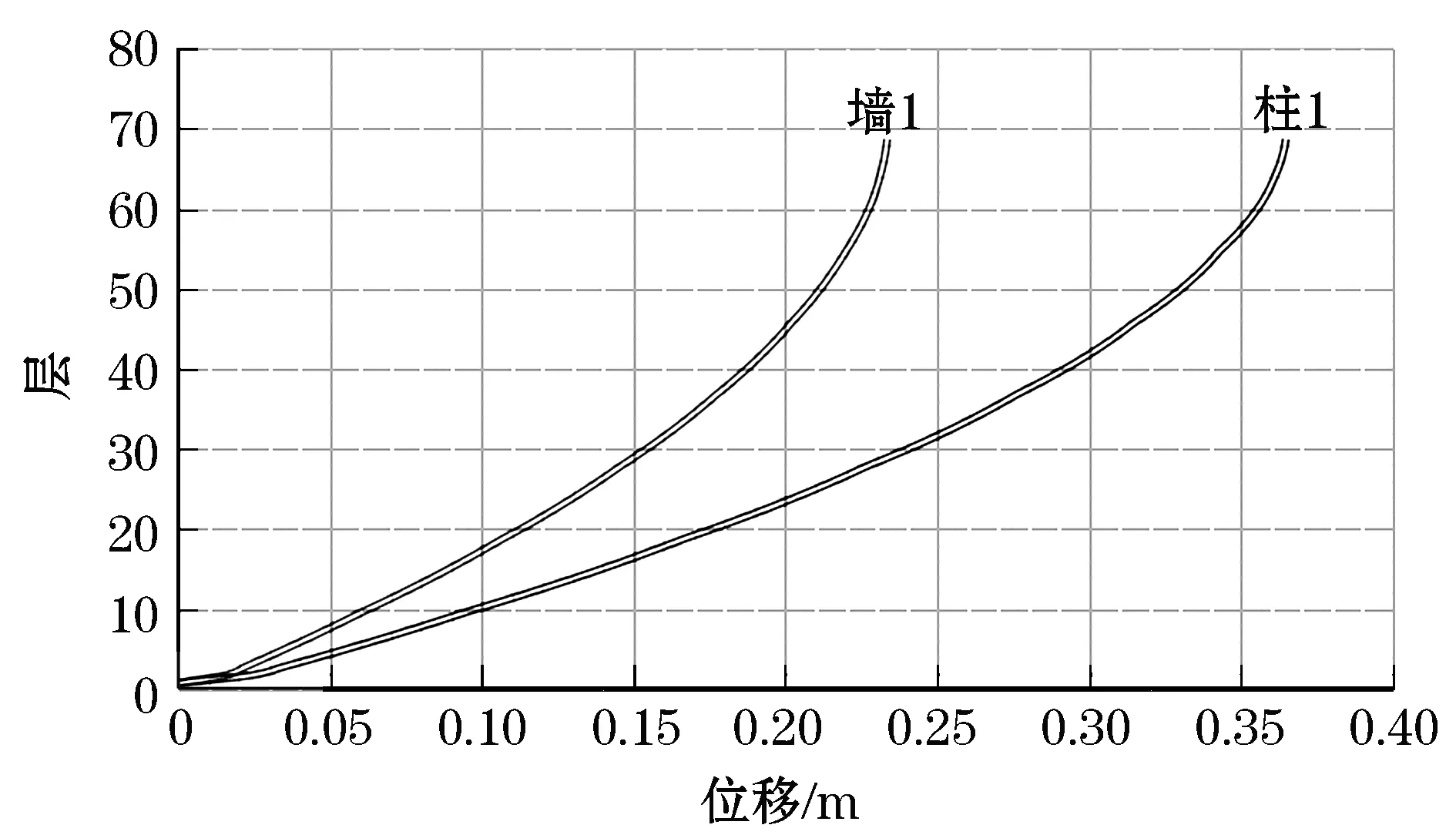
图5 墙1与柱1施工阶段变形图
5 结 论
本文使用的建筑有限元软件Midas/gen具备操作功能上的优势,能定义时间依存性材料、考虑混凝土抗压强度及徐变收缩、模拟建筑结构的施工阶段.对高层结构的施工过程进行模拟,分析徐变收缩对水平、竖向构件的影响,得到结论:1)混凝土徐变收缩增加了梁在墙柱间内力重分布的传力作用,且其导致梁内弯矩增加的幅度随楼层高度增加而增大;2)混凝土徐变收缩对剪力墙和钢管-砼柱的影响是随楼层高度增加而增大.
通过分析了施工阶段钢管混凝土柱的变形值,得到结论是混凝土徐变收缩占总变形的比值较大,其对高层结构的影响较大;通过分析由徐变收缩作用引起的墙、柱竖向变形差,与合计荷载工况下的墙、柱总变形差之比,论证了混凝土徐变收缩对高层结构变形的作用明显,且变形差值是随楼层的增高而增大,该情况下收缩徐变将导致建筑上部楼层的墙柱构件出现裂缝,梁内弯矩增大等不利影响,需要在考虑施工阶段混凝土徐变收缩因素以及构件受力特性的基础上,对层间结构进行加强,于加强层增设伸臂桁架、腰桁架.
