基于交通冲突理论的道路隔离设施设置研究

徐 海，曾铖泓，谢成光，徐锦强，郭建钢

(福建农林大学 交通与土木工程学院，福州 350002)

道路隔离设施具有保障交通安全和道路通行的能力.研究表明，设置道路隔离设施后，交通冲突率降低66%，机动车行车速度提高约15%[1].现有的研究主要为道路交通安全影响因素分析、隔离设施应用效果及安全评价、冲突模型研究等三个方面.丁柏群、刘辉、张诗雯等[2-4]研究信控、无信控交叉口和车辆类型对交叉口安全性影响；蒋若曦、李明华、余忠磊等[5-7]基于交通冲突理论分别研究了高速施工区、铁道口、城市交叉口三者的安全性评价；高志军、马艳丽等[8-9]研究了城市交叉口非机动车、匝道合流区交通冲突及严重评判模型，为今后交通冲突研究提供理论支撑.

但是，目前在我国还没有对交通隔离设施的设置条件进行定量的、精确的分析论述.本文在交通冲突理论的基础上综合考虑不同交通冲突类型对路段交通的影响，使用层次分析法建立在机非隔离和中央隔离设施条件下的路段综合冲突率模型；通过实地数据调查，对各个路段的交通综合冲突率、通行能力以及通行能力变化率进行关联性分析，结合城市交通安全分级标准，得到机非隔离和中央隔离设施设置条件的定量指标.该方法解决了现状道路隔离设施设置条件无具体参考值的问题，有助于道路交通管理者更加合理、有效的管理混行交通流.

1 路段综合冲突率模型的建立

1.1 路段综合交通冲突率

研究中常以冲突率指标来评价交通安全问题[10].以冲突率为指标的城市交通安全分级标准[11]如表1，通过表1可判断路段安全状态，进而判断是否增设道路隔离设施.

表1 以冲突率为指标的城市交通安全分级标准

路段综合冲突率综合考虑行人影响、非机动车影响、机动车影响三大因素，弥补了传统冲突率仅考虑单因素的不足，更综合反映路段冲突问题，具体模型为：

R=α*R机-机+β*R机-非+γ*R机-人

(1)

其中：α、β、γ分别表示三种冲突方式在综合冲突模型中所占权重，机-机、机-非、机-人冲突率可按式(2)[12]进行计算：

(2)

其中：Ri-j为冲突对象i和冲突对象j之间的交通冲突率；T为路段小时平均冲突数；Pi和Pj为参与对象i和j的交通量.

1.2 综合冲突率权重体系的构建

使用层次分析法建立路段综合冲突率权重体系，将路段综合冲突率定为目标层；将行人影响、非机动车影响、机动车影响三大因素作为决策准则层；将机-机冲突、机-非冲突和机-人冲突各自所占权重作为方案层.路段综合冲突率权重体系见图1.

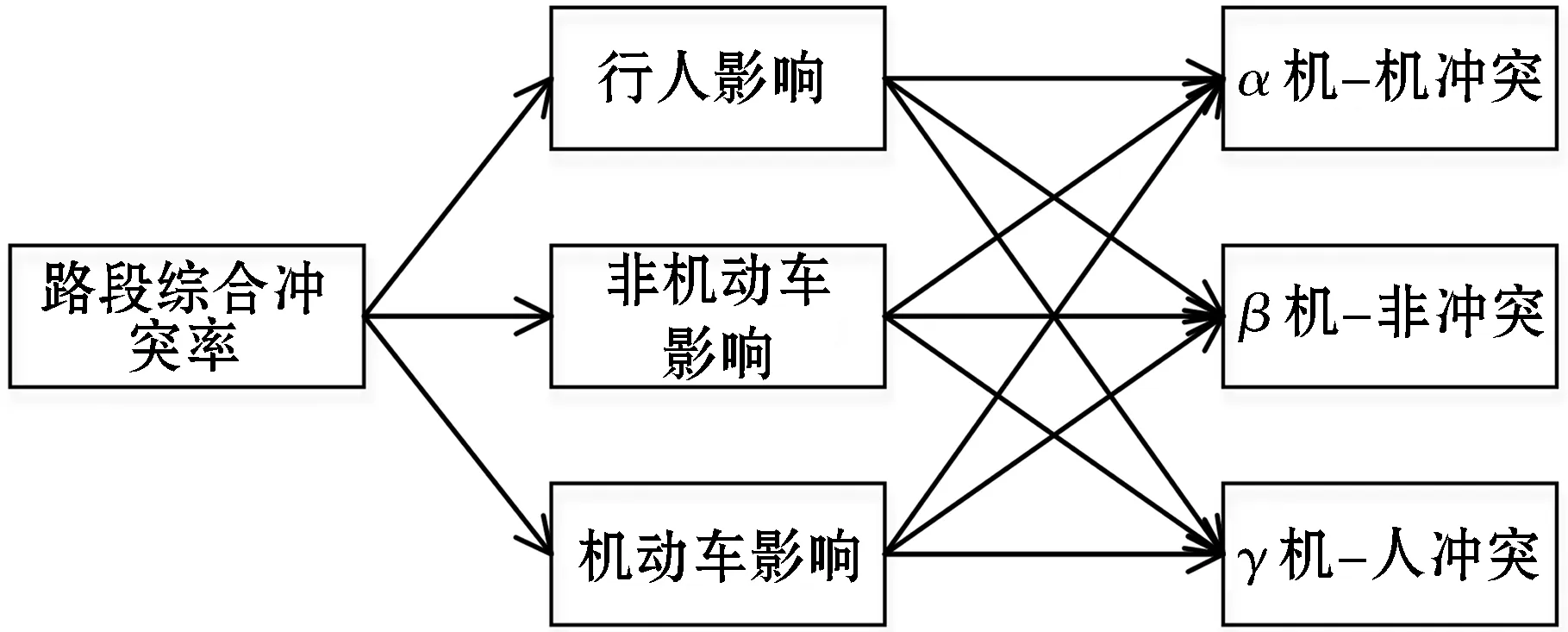
图1 路段综合冲突率权重体系

1.2.1 构建判断矩阵

层次分析法中构造判断矩阵采用一致矩阵法，两两相互比较，对比时采用相对尺度.传统层次分析法有三标度法[13]和九标度法[14-15]，但三标度法的赋值层次过于简单，而九标度法的赋值层次又过于复杂，人类的主观感知无法进行准确判断.因此，研究过程中需要对层次分析法的赋值层次重新定义.由于人脑的逻辑很容易判断“较重要”和“非常重要”这两个层次，而“重要”这一层次便可以此界定.该层次划分方法更容易被人类逻辑所接受，故本文采用四标度法进行赋值，赋值表见表2.

表2 四标度法赋值原则

以机-非隔离设施设置条件为例，根据图1中评价指标体系，构建中层比较矩阵A3×3；针对决策层和方案层间多目标关系，构建底层比较矩阵B1(3×3)、B2(3×3)、B3(3×3).

1.2.2 一级指标权重计算

1)根据四标度法原则，构建道路隔离设施效果评价一级指标的比较矩阵A3×3.

2)对A3×3进行列归一和行归一，归一结果见表3.

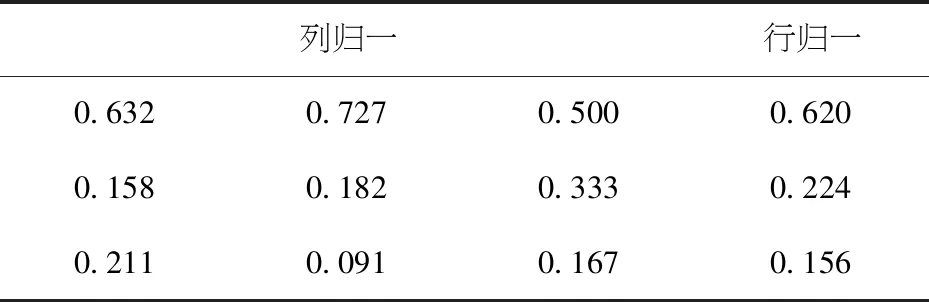
表3 综合冲突率权重体系一级指标归一结果

其中该道路隔离设施效果评价一级指标的比较矩阵A3×3的特征值λ为3.109，特征向量W1=(0620,0.224,0.156)T.

3)一致性指标检验.引入一致性指标CI，定义一致性比率CR.

(3)

(4)

其中：n为矩阵阶层，RI为随机一致性指标.查表当n为3时，RI取0.58，计算结果CR为0.094，小于0.1，故道路隔离设施效果评价一级指标权重为W1=(0.620,0.224,0.156)T.

1.2.3 二级指标权重计算

1)根据四标度法原则，构建路段综合冲突率权重体系二级指标的比较矩阵B1(3×3)、B2(3×3)、B3(3×3).

2)对A3×3进行列归一和行归一，归一结果见表4.

其中：该道路隔离设施效果评价二级指标的比较矩阵B1(3×3)、B2(3×3)、B3(3×3)的特征值λ为λ21=3.054、λ22=3.018、λ23=3.009，对应特征向量分解为W21=(0.655,0.211,0.133)T、W22=(0.623,0.239,0.137)T、W22=(0.623,0.192,0.175)T.

表4 路段综合冲突率权重体系二级指标归一结果

3)一致性指标检验.查表当n为3时，RI取0.58，计算结果CR为CR1=0.047、CR2=0.016、CR3=0.008，均小于0.1，故道路隔离设施效果评价二级指标权重为W21=(0.655,0.211,0.133)T、W22=(0.623,0.239,0.137)T、W23=(0.623,0.192,0.175)T.

1.3 模型综合权重指标确定

二级指标权重计算得到的W21、W22、W23组成3×3阶矩阵，记为W3.

故机-非隔离设施条件下，路段综合冲突率模型确定为：

R1=0.644*R机-机+0.214*R机-非+0.140*R机-人

(5)

同理，中央隔离设施条件下，路段综合冲突率模型确定为：

R2=0.140*R机-机+0.304*R机-非+0.556*R机-人

(6)

2 数据收集和统计

以福州市作为案例分析对象.选取标线隔离设施、机非物理隔离设施和中央物理隔离设施这3类隔离设施的路段，进行交通量和交通冲突数的数据调查，并进行冲突率、通行能力等计算.交通量、交通冲突数、路段交通冲突率、路段通行能力统计表见表5、6.

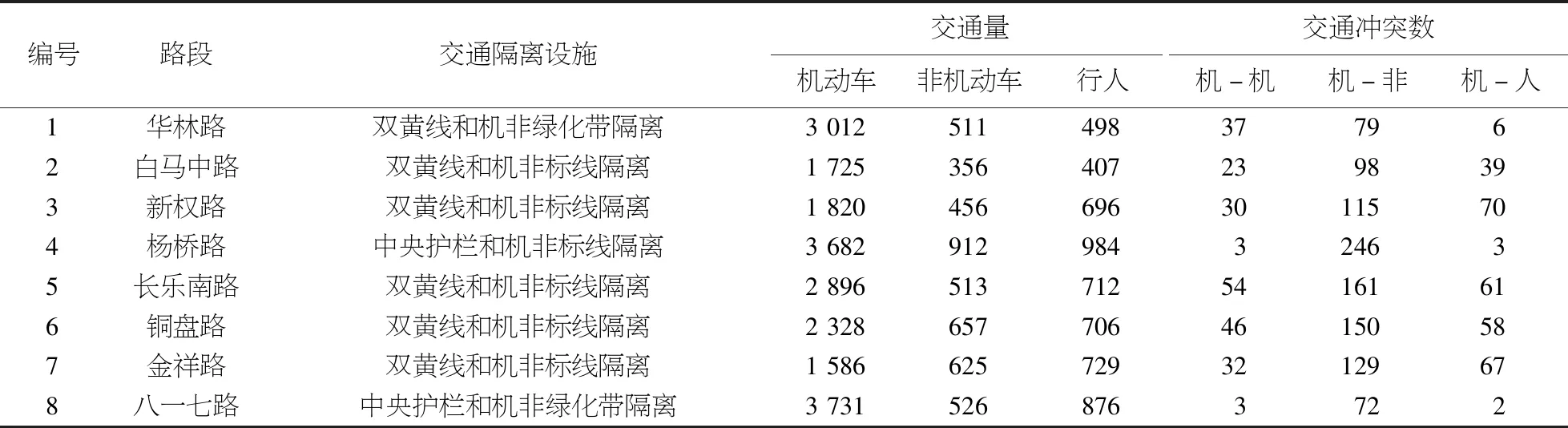
表5 交通量、交通冲突数统计表

注：“机-机”为路段上机动车与机动车交通冲突的次数；“机-非”为路段上机动车与非机动车交通冲突的次数；“机-人”为路段上机动车与行人交通冲突的次数.

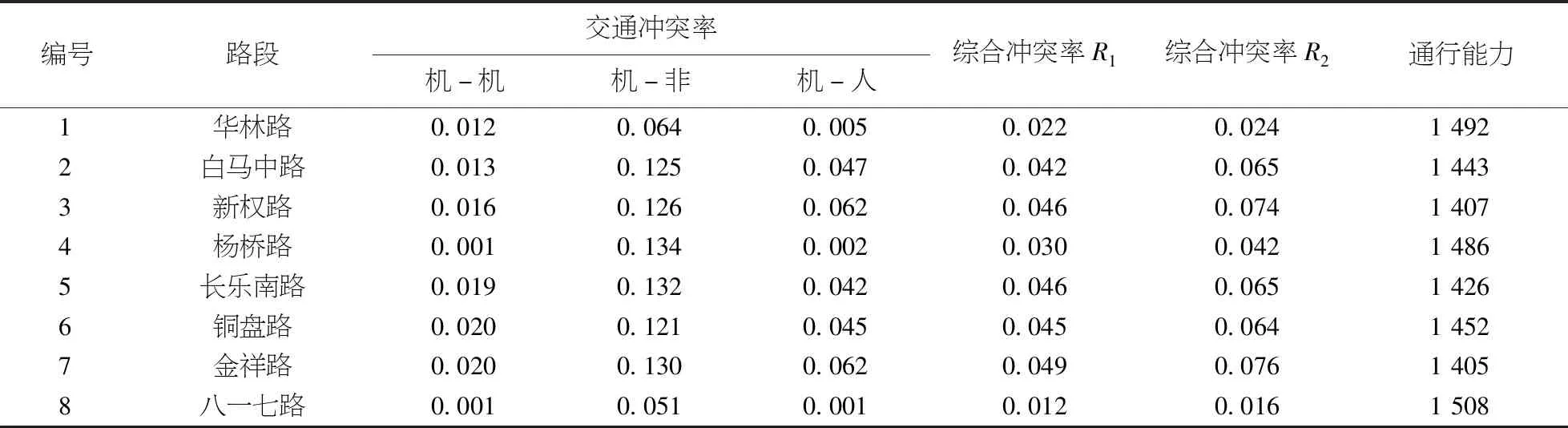
表6 交通冲突率和通行能力统计

3 结果分析

3.1 机-非物理隔离设施条件分析

根据城市交通安全分级标准，冲突率大于0.03，判定为不安全状态，故机-非物理隔离设施条件下的路段隔离设施存在安全隐患.现对各个路段的交通综合冲突率和机动车通行能力、通行能力变化率进行关联性分析，如图2、3所示.

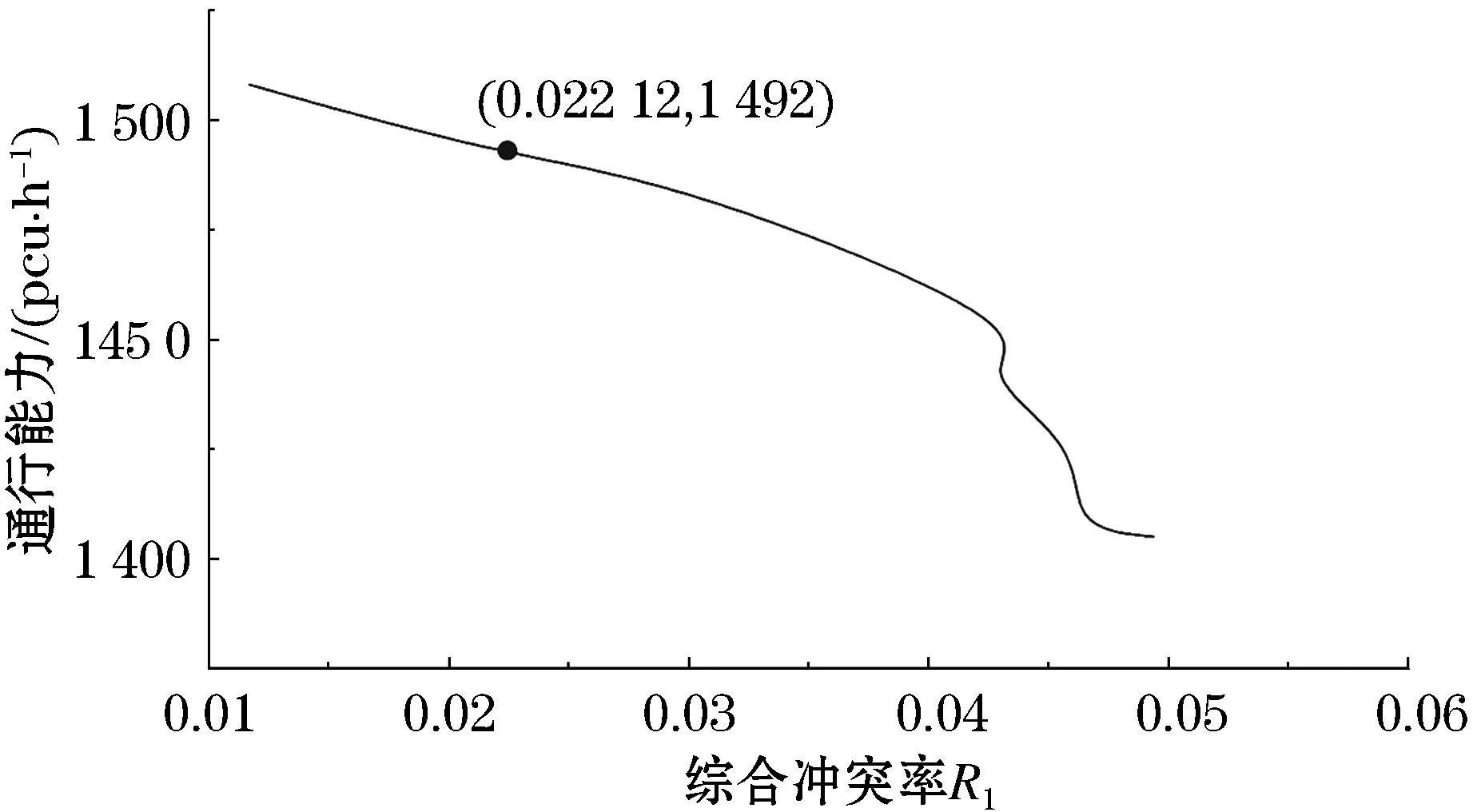
图2 综合冲突率-通行能力关联曲线

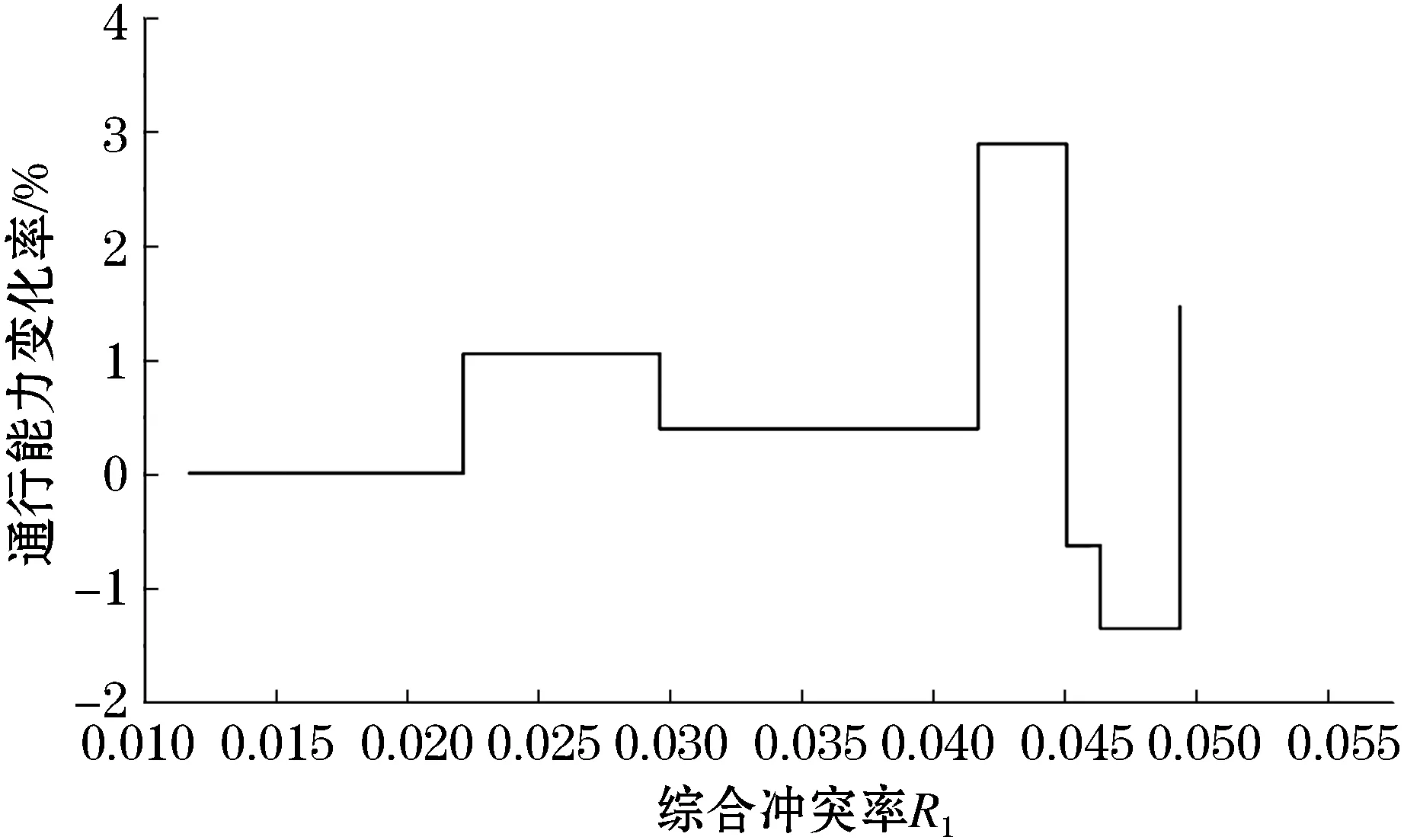
图3 综合冲突率-通行能力变化率分布

图2中标明的坐标点为有无设置机非物理隔离设施分界点.当路段交通综合冲突率小于0.022时，设有机非隔离设施.结合图2、3可以看出，路段通行能力较大，但数值变化率保持不变；当路段交通综合冲突率大于0.022时，未设置机非隔离设施.此时由图2、3可以看出，综合冲突率在0.022～0.043时，路段通行能力在下降，但数值变化率较小，此时可设机非隔离设施；综合冲突率在0.043～0.053时，路段通行能力在下降，且数值变化率较大，此时须设机非隔离设施.

3.2 中央物理隔离设施条件分析

根据城市交通安全分级标准，冲突率大于0.03，判定为不安全状态，故中央隔离设施条件下的路段隔离设施存在安全隐患.现对各个路段的交通综合冲突率和机动车通行能力、通行能力变化率进行关联性分析，如图4、5所示.

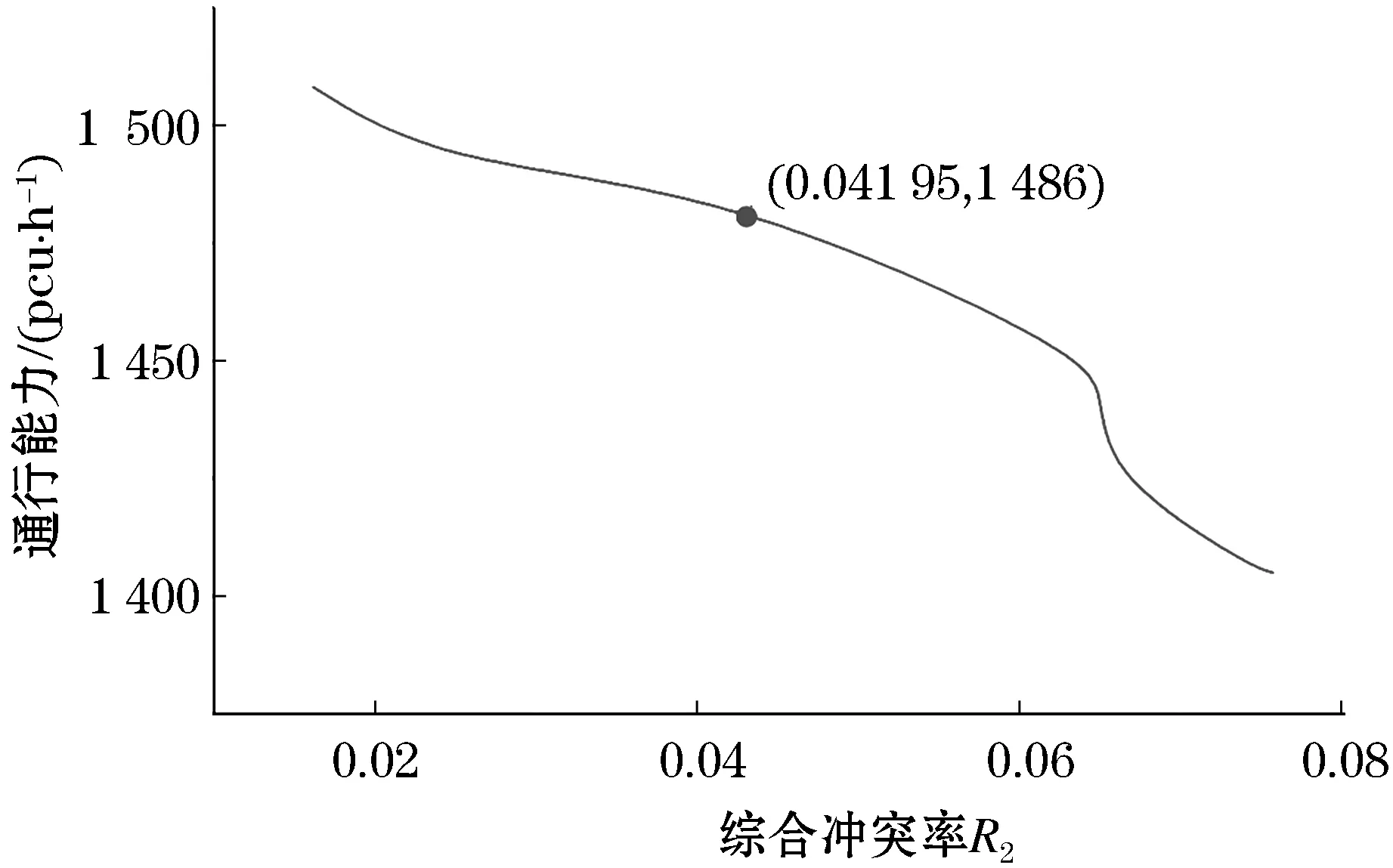
图4 综合冲突率-通行能力关联曲线

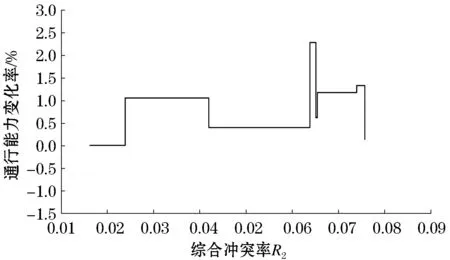
图5 综合冲突率-通行能力变化率分布

图4中标明的坐标点为有无设置中央物理隔离设施分界点.当路段交通综合冲突率小于0.042时，设有中央隔离设施.结合图4、5可以看出，路段通行能力较大，数值变化率较小；当路段交通综合冲突率大于0.042时，未设置中央隔离设施.此时由图4、5可以看出，综合冲突率在0.042～0.063时，路段通行能力在下降，但数值变化率保持不变，此时可设中央隔离设施；综合冲突率在0.063～0.080时，路段通行能力在下降，且数值变化率波动较大，此时须设中央隔离设施.

3.3 分析结论

通过路段综合冲突率-通行能力和路段综合冲突率-通行能力变化率的关联性分析，得到在不同综合冲突率指标下道路隔离设施的设置建议，主要分为机非隔离设施和中央隔离设施设置两类.道路隔离设施定量设置指标见表7.

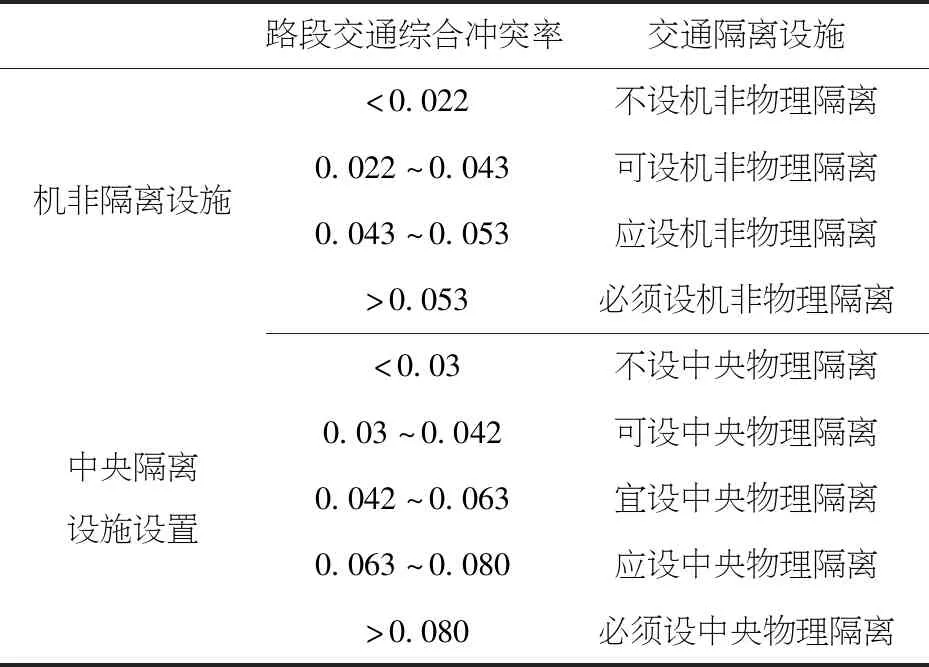
表7 道路交通隔离设施设置依据

4 结 语

本文综合考虑机-机冲突、机-非冲突和机-人冲突三种因素对道路交通的影响，通过改进AHP建立交通综合交通冲突模型，结合以冲突率为指标的城市交通安全分级标准，可为道路交通安全评价提高更加科学的方法，但仍存在问题需要进一步探讨：

1)数据调查中，道路隔离设施种类较少，后续需扩大调查范围；

2)以福州地区的路段隔离设施为分析对象，得到的隔离设施设置条件，缺乏其他城市道路隔离设施数据的验证，后续将调查其他城市隔离设施设置情况，进一步验证本文结论.