基于CEEMDAN的塌落触地振动信号最优降噪光滑模型算法*

赵明生，苟倩倩，张光雄，池恩安，胡娟新,姚颖康

(1.保利新联爆破工程集团有限公司，贵阳 550002；2.贵州大学 矿业学院，贵阳 550025； 3.保利民爆哈密有限公司，哈密 839000；4.武汉爆破有限公司，武汉 430000)

随着安全环保意识的提高，对城镇爆破拆除作业所带来的塌落触地振动危害控制越来越严格。在建(构)筑物倒塌过程中，炸药释放的能量使得部分构件解体，造成上部结构失去稳定性从而塌落，触地冲击地面瞬间会产生很大的能量，其中，部分能量促使地面介质产生振动，以地震波的形式向外传播，并在地表产生震动[1]。由于受爆破地震波监测点的随机性、仪器误差、磁场干扰、传播介质等因素影响，使爆破振动信号携带一定的噪声，难以精确识别其模态信息，从而影响振动危害评价的准确度。

目前，爆破振动信号降噪主要采取二代小波变换、集合经验模态分解及集合经验模态分解和小波阈值共同作用等方法[2-4]，小波变换分析法有效性很大程度上依赖小波基函数的选取，存在一定程度的主观因素影响[5]。集成经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)是在原始信号中多次添加不同白噪声，分别进行EMD分解，然后对多次 EMD 分解的 IMF 进行平均而得到最终的实际分量，它能有效地改善EMD方法所存在的模态混叠现象[6]。但是EEMD在信号重构时存在完备性不足，且计算耗时长的问题[7-9]。近年来，由Torres提出的具有自适应噪声的完整集成经验模态分解[10](Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,CEEMDAN)，通过在每个阶段添加有限次的自适应白噪声，计算唯一余项信号获取IMF，实现在较少的平均次数下，几乎完全重构分解后的固有模态，实现精确的信号特征提取。该方法能有效解决EMD分解的模态混叠问题，同时还能克服EEMD分解的完备性较差及多次增加集成次数来降低重构误差而导致的计算效率低的问题[11-13]。

基于此，提出一种基于CEEMDAN的爆破振动信号最优光滑降噪算法，以设计仿真信号为研究对象，将其分别进行EMD、EEMD及CEEMDAN的最优光滑降噪算法效果对比，并将该算法应用于实测水塔爆破触地振动信号降噪分析。

1 建立最优降噪光滑模型

1.1 设计滤波器

将原始含噪信号进行CEEMDAN分解后的IMF分量进行高通、低通、带通滤波器的组合设计[14]。其中，高通滤波常用来于增强高音成分以驱动扬声器的高音单元，低通滤波可以增强中音成分，而带通滤波可以对特定频率范围内的信号进行筛选，达到选择性传输的目的。

高通滤波器可设计为

(1)

低通滤波器可设计为

(2)

带通滤波器可设计为

(3)

式中：a、q为滤波器的上截断参数；b、p为滤波器的下截断参数，其取值应根据不同信号的滤波要求来优化确定。

假设由CEEMDAN分解出的固有模态分量IMF有N个，则具体的滤波器算法表达式为

A1=s(n)-IMF1

A2=s(n)-IMF1-IMF2

A3=s(n)-IMF1-IMF2-IMF3

⋮

An=s(n)-IMF1-IMF2-IMF3-…-IMFn

(4)

1.2 定义降噪偏均方误差

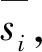
(5)

由定义可知，降噪均方误差越小，降噪后的曲线越接近原始信号，即两个曲线相似度越高。

1.3 定义曲线曲折度

设有两条曲线P(t)、q(t)(0≤t≤1)，如果曲线P在点P(1)处的二阶倒数等于曲线Q在点Q(0)的二阶倒数，则曲线光滑。

(6)

将点P(1)、Q(0)处的二阶倒数按照离散公式展开得

(7)

(8)

由于曲线光滑，则点P(1)、Q(0)一阶导数相等，即可得到在x=x0点处的光滑指标

SNx=x0=f(x0+2h)-f(x0-2h)-

2[f(x0+h)-f(x0-h)]

(9)

式中：h为步长，取值1；当x0趋于零时，x0附近的点对应曲线越光滑，即曲线的曲折度越小，信号越光滑。

1.4 基于CEEMDAN最优降噪光滑模型判定准则

在模型的建立中，降噪偏差均方差MSEf的值越小，降噪后的信号与原始信号相似度越高，同时滤波算法的光滑性指标SMSEf的值越小，曲线越光滑，即目标函数值越小降噪效果越好。基于此，建立约束条件

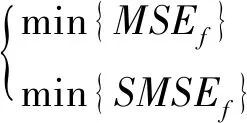
(10)

则爆破振动信号滤波算法目标函数可以写成

min{f}=min{αSMSEf+(1-α)MSEf}

(11)

式中，α为曲线降噪均方误差权重因子，1-α为曲线曲折度权重因子，其取值按照信号处理过程中具体要求而定。基于CEEMDAN的最优光滑降噪流程如图1所示。

2 仿真信号降噪分析

设计仿真信号对上述降噪算法进行验证，仿真信号Y(t)分别由低频正弦信号x1，调频信号x2及功率为0.01的高斯白噪声x3合成。

(12)

式中:t=[0,4]，采样频率为2000 Hz，各组成信号及混合仿真信号时域波形如图2所示。

对仿真信号分别进行EMD、EEMD及CEEMDAN分解。其中，EMD分解得到10个固有模态分量一个余项，EEMD分解得到12个固有模态分量及一个余项，CEEMDAN分解后得到13个固有模态分量及余项。按照式(4)EMD分解将会产生11个带通滤波算法，同理，EEMD及CEEMDAN分解分别产生13和14个带通滤波算法，将仿真信号分别用三种方法分解后组成的算法进行降噪处理，求出每个算法的降噪均方误差及光滑度，按照约束条件确定目标函数值，并进行归一化处理，当曲线降噪均方误差权重因子取0.5时，三种方法分解后组成的算法的降噪误差曲线如图2～图4所示。

结合图2至图4可以看出：当降噪均方误差权重因子取0.5时，基于EMD分解的11个算法中，A2算法目标函数值最小，其值为0.1653；基于EEMD分解的13个算法中，A2算法目标函数值最小，其值为0.3179；基于CEEMDAN分解的14个算法中，A4算法目标函数值最小，其值为0.1353，即基于CEEMDAN分解的A4算法的目标函数值最小，降噪效果最好。图2至图4中目标函数曲线在算法A10之后几乎都趋于平衡，这是由于从A10算法之后减去的固有模态分量都是低频，而高频噪声在算法A10之前几乎被完全过滤掉。

图5为基于CEEMDAN分解的算法A4、A5、A6、A7降噪的仿真信号与原始仿真信号，由图可以看出：经算法A4降噪的信号在低频部分明显比原仿真信号光滑，并且重构后的信号几乎与原仿真信号重合，算法A5仅次于算法A4，而经算法A6、A7降噪的信号在1 s之后频率明显较低，出现了过度降噪的情况，与原始仿真信号差别较大。

图6可以直观的看出CEEMDAN分解的A4算法降噪重构的仿真信号比原始信号光滑且相似度高，降噪信号与未加噪信号x3相关度高达0.9969；并且重构信号与降噪信号之差与原始(x1+x2)噪声信号极其相似，其相关度为0.9134，降噪效果较好。

表1计算出三种方法分解下组成的最优算法的含噪信号与降噪误差比，CEEMDA分解的A4算法的值最小，该值越小，降噪误差越大，降噪信号越偏离含噪信号，则降噪效果越好。

实际上，当降噪均方误差权重分别取0.1～0.3时，基于CEEMDAN分解的算法A5都最优，其次是算法A4；当降噪均方误差权重分别取0.4～0.9时，算法A4最优。图7为降噪均方误差权重因子分别取0.1～0.9时，CEEMDAN分解的14个降噪算法对应的目标函数，由图可以看出：在14个算法中，算法A4的平均目标函数值最小。

表1 含噪信号与降噪误差比Table 1 Noise signal to noise reduction error ratio

3 塌落触地振动信号时频分析

为了验证算法的实用性，以实测水塔爆破触地振动信号为依据，对其进行基于CEEMDAN的最优降噪光滑模型算法降噪后进行希尔伯特变换对比不同测点的频率及能量分布。

3.1 工程概况

待拆除水塔高38.1 m，其中，塔身高28.6 m，倒锥伞形水箱高9.5 m。水塔下部支筒为圆筒形，筒体内径为2.0 m，壁厚0.18 m，筒内设有5个设备检修平台，上部水箱为倒锥形结构，伞形水箱最外径为10.64 m。水塔筒体及水箱配有主筋和箍筋，为研究高耸构筑物触地振动规律，采用原地坍塌总体爆破方案，爆破切口布设在水塔底部以及各层检修平台处，共计6个爆破切口，其结构示意图及切口布置如图8所示，起爆网路延期时间如表2所示。利用TC-4850N爆破测振仪实测其速度(仪器采样频率设置2000 Hz，采样时长6 s)，振动测点布置如图9所示，振动监测数据如表3所示，其中三个测点信号三向合速度依次记为S1、S2、S3，降噪后的信号记为S1-1、S2-2、S3-3。

3.2 信号降噪

针对实测的信号S1、S2、S3进行CEEMDAN分解后分别得到13个固有模态分量IMF及余项r(t)，同样产生14个带通滤波算法，考虑到触地振动频率一般在1～10 Hz，属于低频率[15]，滤波之后光滑度权重大于相似度，所以均方降噪误差权重因子取值0.3或0.4较为合理。当α=0.3时，14个带通算法的降噪均方误差、折线曲折度、目标函数如图10所示(限于文章篇幅只列取S1信号降噪效果图)。

由图10可看出，当降噪均方误差权重因子取0.3时，算法A4的目标函数值最小，即算法A4的降噪效果最好；由图11可以看出，经算法A4降噪重构后的信号与原始爆破振动信号相似度较高，在2.5～4 s信号幅值有所减小，这可能是水塔塌落过程中结构碰撞或触地引起的噪声；图12截取S1及S1-1信号0～1 s数据，可以看出，基于CEEMDAN分解的A4算法降噪重构后信号比原始信号光滑且相似度高，与仿真信号降噪效果一致。

表2 起爆网路延期时间(单位：ms)Table 2 Detonation network delay time(unit:ms)

表3 水塔爆破触地振动数据监测结果Table 3 Water tower blasting ground vibration data monitoring results

为了进一步说明实测信号在三种方法分解下的降噪效果，表4表计算出三个信号在三种方法分解下组成最优光滑降噪算法的信噪比，相比EMD分解A2算法和EEMD分解A2算法，由CEEMDAN分解的A4算法的信噪比值最小，说明降噪效果最好，与仿真信号降噪效果一致。

3.3 信号边际能量谱分析

对振动信号的边际谱幅值的平方在全局时间上进行积分得到振动信号的边际能量谱，信号边际能量谱上的曲线函数代表在不同频率时信号的总能量幅值。现对降噪后的S1-1、S2-2、S3-3水平信号进行希尔伯特-黄变换，得到其边际能量谱，如图13所示。

表4 含噪信号与降噪误差比Table 4 Noise signal to noise reduction error ratio

由图13可以看出：信号S1-1、S2-2、S3-3边际谱在频率为5 Hz左右处能量出现最大值，说明其在频率5Hz附近能量最集中；在能量达到最大值后紧接着又出现了两个幅值较大的曲线，这主要是由于切口之间爆破时间间隔小，前后切口爆破倒塌触地产生的冲击波累加导致频率有所增大。信号S1-1,S2-2,S3-3的边际能量谱幅值逐渐的减小，也间接的说明振动波的能量在传播过程中在不断地衰减，并且随着传播距离的增加衰减速度逐渐变慢。

3.4 信号三维时频能量谱分析

为直观的看到降噪后信号的时频、能量分布，截取前4 s的S1-1、S2-2、S3-3水平信号再次经过CEEMDAN分解后，进一步进行希尔伯特黄变换得到三维时频能量谱，如图14所示。

由图13可以看出，经塌落触地振动信号的主要频率集中在频率0～20 Hz的频带内，大于20 Hz的频带内携带的能量较少；偶尔在高频带段内有时会突然出现局域能量峰值，通过峰值以后迅速衰减，这一现象表明塌落触地振动产生的地震波在高频部分衰减速度比在低频部分的衰减速度要快；随着测点距离增加，能量向低频带集中，并且3 s后各频带所携带能量明显减少；塌落触地振动波在传播过程中不同频带能量的持续时间不同，低频部分振动波持续时间更长，几乎贯穿地震波传播的整个过程，这表明振动波主要以低频波携带的能量为主。

4 结论

实测的非平稳爆破振动信号往往夹杂较大的噪声，因此，信号降噪在原始信号特征提取时显得尤为重要，本文将仿真信号分别进行EMD、EEMD、CEEMDAN分解，通过设计合理的滤波器，得到不同条件下的滤波算法，根据降噪均方误差指标、曲线曲折度指标建立最优光滑降噪算法的判断准则，最终确定基于CEEMDAN分解得到的算法A4降噪效果最好，其信噪比值最小。

将实测塌落触地振动信号进行降噪处理，对比分析了三种分解方法下信号S1的信噪比，结果表明，基于CEEMDAN分解的最优降噪算法信噪比值最小，验证了该算法模型具有良好的降噪能力以及工程实用性，为实现精细爆破及提高振动危害评价的准确度都具有一定的应用价值。

对降噪后的触地振动信号进行时频分析，结果表明，塌落触地振动信号的主要频率集中在频率0～20 Hz的频带，且随着距离的增加能量向低频带集中。