高陡边坡动力响应研究*

季金铭，高文学，曹晓立，叶明班，张登杰

(北京工业大学 建筑工程学院，北京 100124)

爆破是边坡工程、道路工程、水利水电工程中常用的施工方法，爆破振动诱发的边坡崩塌、滑移等严重影响人民的生命财产安全，因此对于边坡的动力响应研究具有十分重要的现实意义[1,2]。目前，国内外学者针对这一课题进行了广泛研究，主要侧重于振速的高程放大效应研究。唐海等研究发现凸形地形、地貌对爆破振动波的放大效应具有方向性[3]，并运用量纲分析法推导了反映高程放大效应的爆破振动公式。陈明等依托溪洛渡水电站右岸坝肩爆破工程，通过理论分析及数值模拟得到在边坡坡形骤变、坡度增大的坡段会产生显著的振动速度高程放大效应[4]。付波等基于LS-DYNA的动力有限元计算，得出马道外缘点和马道中点出现明显的振动放大效应[5]，而马道内测点和坡面中点的爆破振动放大并不明显。武旭等基于台阶地形爆炸振动数值模拟与边坡振动实验，得出台阶高程对爆破振动速度既有放大作用同时也随高度的增加产生衰减作用[6]。万鹏鹏等通过现场监测数据得出正高差边坡在爆破振动荷载作用下产生“鞭梢效应”[7]，使台阶突出部位岩体产生显著的高程放大效应。国外方面，Marrara、Havenith及Vladimir等对边坡的动力响应进行了相关研究[8-10]。

以往研究者在一定程度上探明了边坡在爆破荷载作用下的动力响应规律，但由于边坡的动力响应受地形地貌等因素影响，这些规律不具有普适性，因此有必要对高陡边坡在爆破开挖过程中边坡的动力响应进行进一步的深入研究。本文依托高山滑雪中心索道平台处高陡边坡爆破工程，通过现场振动监测和有限元软件模拟分析了爆破荷载作用下坡顶及坡面质点振速、应力、位移衰减规律，为后续爆破开挖设计与边坡支护提供依据。

1 现场测试

1.1 场地概况

本次爆破位于国家高山滑雪中心(延庆赛区)C1索道平台处，原始地貌坡度在20°至45°之间。依据现场地质勘查，山坡表层为耕植土和碎石土，厚度约为1～2 m。表层以下为节理裂隙较发育的花岗岩。开挖分为四级放坡，坡高依次为4.4 m、9 m、9 m、8.3 m，台阶平台宽2 m，边坡设计坡比为1∶0.3。本次爆破在第三级边坡处。

1.2 爆破设计及振动监测

爆破设计参数如下：钻孔直径φ=100 mm，孔距a=3～3.5 m，排距b=2.5～3 m，爆破抵抗线W=2.5～3 m，最大单段药量为792 kg。采用逐排起爆网路，共计6排炮孔，最外一排首先起爆，由外向内依次起爆。

爆破振动监测采用TC-4850测振仪，依据工程施工进度和地形条件，爆破振动监测点布置在边坡坡顶，第一个测点距离边坡外沿3 m处，其余三个测点间隔5 m依次布置，测点布置如图1、图2所示。

1.3 振动规律分析

本次爆破中采集的4个测点的振速峰值统计数据如表1所示。

表1 测点峰值振速统计表Table 1 Statistical table of peak vibration velocity at measured points

对三个方向的振速峰值按萨道夫斯基公式进行非线性拟合[11-13]，拟合结果如图3和表2所示。

(1)

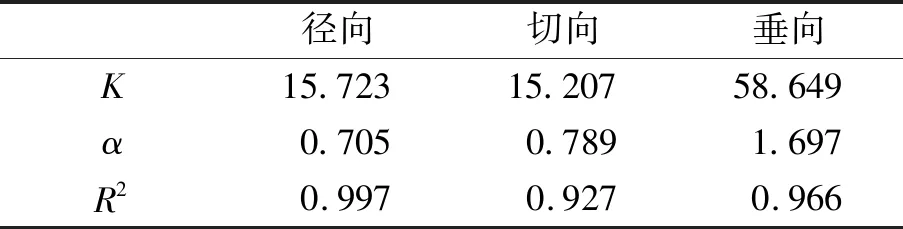
表2 回归参数表Table 2 Regression parameter table

拟合结果显示，三个方向拟合优度R2均大于0.9，拟合效果较好，具有较高的可靠度，拟合公式能够应用于实际工程。

从图3可以看出，在爆心距小于35 m范围内V垂向>V径向>V切向，且随着爆心距的增大，三个方向振速逐渐减小。从振速峰值衰减速度上看，垂向振速衰减最快，切向振速和径向振速衰减较慢。

岩体爆破开挖过程中对岩体及周边建(构)筑物的爆破振动破坏作用不仅取决于峰值振速，而且和爆破振动波的振动频率以及持续时间密切相关。对四个测点垂向振速进行傅里叶变换得到频谱图,如图4所示。

图中可以看出爆破地震波的主要频率范围在50 Hz以下，主要频率范围随着传播距离的增加逐渐变窄，并向低频的方向移动。同时，振动主频随着距离的增加也会衰减，爆破地震波通过岩体结构面时高频部分比低频部分更容易被滤掉，使得爆破地震波高频部分的能量衰减快于低频，高频部分携带的能量逐渐减小，能量向低频方向集中。

对于岩质边坡，《爆破安全规程》(GB6722—2014)[14]中，根据爆破主振频率的不同，给出了边坡振动速度控制标准如表3。

表3 边坡爆破振动安全允许标准Table 3 Safety criterion of blasting vibration for rock slope

本次爆破施工过程中，主频在10～50 Hz，除1#测点垂向振速大于12 cm/s，其余测点振速峰值均在安全允许范围内。爆破现场发现坡面有碎石塌落现象，但坡顶平面岩体没有明显损伤，边坡处于安全状态。

2 岩质边坡爆破振动数值模拟研究

2.1 模型的建立及边界条件

依据现场的实际情况和对边坡的初步分析，建立如下的三维模型：模型分为两个区域，表层为中等风化的花岗岩，以下为微风化的花岗岩，共86 724个有限单元，模型两侧添加自由场边界，底部采用固定约束。为保证计算精度，炮孔周边网格尺寸取0.04 m，边坡坡面取0.5 m，模型远处边界尺寸为2.5 m，模型尺寸图如图5所示。

2.2 材料模型及参数

本模型采用理想弹塑性模型，基于摩尔-库伦屈服准则。具体岩石物理力学参数如表4。

表4 岩石物理力学参数表Table 4 Rock physical mechanics parameter table

2.3 边界及爆破荷载的确定

采用三角形荷载曲线模型加载到炮孔壁上，对于耦合装药，荷载峰值等效荷载由式(2)、(3)计算[15]

(2)

(3)

式中：Pw为药包中心爆轰波产生的平均初始压力，N/m2；r为比例半径，r=R/Rw，R为与药包轴线的距离，Rw为药包横切半径；α为与岩体介质和炸药种类有关的常数，一般取1.5；ρw为装药密度；D为炸药爆轰速度；K为等熵指数，与装药密度有关，当ρw<1.2 g/cm3时，K=2.1，ρw>1.2g/cm3时，K=3。

爆破荷载升压时间tr由式(4)计算

(4)

爆破荷载压力正压作用时间ts由式(5)计算

(5)

式中：EV为岩体体积压缩模量，MPa；μ为岩体泊松比；Q为装药量，kg，计算得到荷载时程图如图6所示。

2.4 数值模拟结果分析

表5给出计算模型对应四个测点处的峰值振速实测值与模拟值的误差。

误差分析可以看出，1#测点模拟值与检测值基本吻合，但是随着水平爆心距的增大，测点误差也逐渐增大，这是由于数值模拟假定边坡岩层为均质理想岩体，而实际岩层内部存在节理、裂隙，这些节理、裂隙会吸收爆破地震波的能量导致应力波明显衰减。虽然测点振速峰值存在误差，但均在合理范围之内，数值模拟的结果可以应用在边坡中。

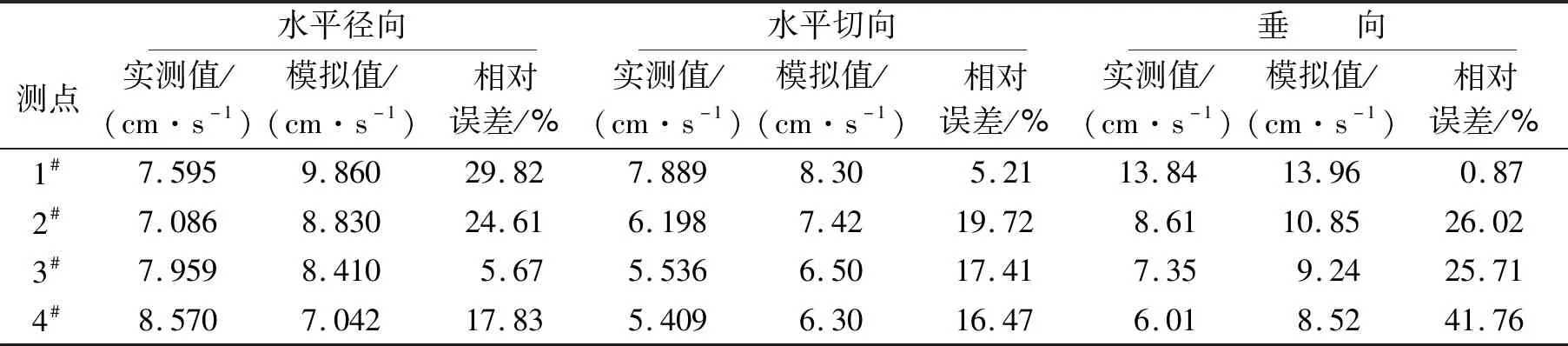
表5 实测值与模拟值对比表Table 5 Table of comparison between measured and simulated values

2.4.1 质点振动速度分析

图7为一个周期的爆破荷载作用下岩体内合速度的变化云图。为更好观察速度场在岩体内部的分布变化，剖取后半侧模型进行分析。

从图7可看出爆破振动产生的速度场以爆源为中心呈环状扩散至整个岩体。扩散过程中地震波能量被岩体介质吸收，为更精确分析岩体爆破地震波的传播规律，提取坡面若干质点作为研究对象，坡面质点的振速峰值曲线如图8所示。

从图8可以看出，质点三向振速及合速度沿坡面总体呈现衰减趋势。在第Ⅰ级台阶和第Ⅱ级台阶处出现明显的波动现象，这是由于爆破振动波传播至台阶处会产生“鞭梢效应”[16-18]，在坡面相同高程处，第Ⅱ级台阶外缘相对于内侧坡脚放大系数分别为合速度1.66、垂向1.67、径向2.17、切向2.24。在沿边坡坡型急剧变化的不同高程处，第Ⅰ级台阶外缘振速相对于第Ⅱ级台阶外缘在合速度向、垂向、径向均体现出明显的高程放大效应，放大系数分别为1.1、1.13、1.15，但在切向上没有表现出高程放大现象。此外，第Ⅰ级台阶坡脚振速相对于第Ⅱ级台阶坡脚也没有出现高程放大现象。

2.4.2 质点应力分布规律分析

图9为一个爆破周期内最大主应力变化云图。爆破荷载作用开始后，爆破应力波以炮孔为中心逐渐扩散到整个边坡，扩散过程中受坡型变化影响，在坡脚处出现应力集中现象，提取坡面最大主应力峰值得到曲线图10。

从图10中可以看出坡面各向最大主应力沿着坡面总体呈现衰减趋势，其中切向主应力受坡型变化影响小。而合主应力、径向主应力、垂向主应力有相似的变化趋势：在第Ⅰ、Ⅱ级台阶平面上，在台阶外缘出现最大主应力极小值，沿着台阶平面逐渐增大，在台阶坡脚处达到极大值。沿着坡面方向上，最大主应力逐渐增大，合主应力和垂向主应力曲线在坡中处略微波动产生小区域放大现象，随后逐渐衰减，在台阶外缘处达到极小值。结合图8可以得出，台阶处速度峰值和应力峰值出现的位置无相关性，因此不应将台阶边缘处质点振速峰值作为边坡稳定性评价的单一指标。在第Ⅰ、Ⅱ级台阶坡脚处总应力大小分别为0.17 MPa、0.27 MPa，两者均小于岩体抗拉强度，故爆破开挖时，坡脚处不会因为应力集中造成岩体破坏。

2.4.3 质点位移场分析

图11为边坡岩体内一个爆破周期内不同时刻位移场变化云图，从图中可以看出，爆破位移场呈环状扩散，质点位移呈现先增大后减小的趋势。提取坡面质点各方向位移图12所示。

与图8坡面振速峰值变化曲线相比，坡面位移变化曲线有相似的变化规律，坡面台阶处位移也受“鞭梢效应”影响，在台阶外缘处边坡位移有增大现象，但从数值来看，产生位移不会对边坡稳定性产生影响。

3 结论

依托国家高山滑雪中心(延庆赛区)索道平台处高陡边坡爆破工程，将现场监测和数值模拟相结合，研究了爆破荷载作用下边坡振速、应力、位移的变化规律，在此基础上分析了爆破施工对边坡安全稳定性的影响，主要结论如下：

1)对于边坡坡顶平面，随着爆心距的增大，质点振速峰值呈衰减趋势，一定范围内V垂向>V径向>V切向，质点垂向振速主频主要集中在0～50 Hz，随着爆心距增大，主频范围逐渐变窄且向低频方向移动。

2)对于边坡坡面质点，随着爆心距增大，质点振速峰值总体呈衰减趋势；台阶处受“鞭梢效应”影响产生放大效果，且放大效果具有方向性；台阶外缘相对台阶内侧，质点振速在合速度向、垂向、径向、切向分别放大1.66、1.67、2.17、2.24倍；上一台阶相对下一台阶，质点振速在合速度向、垂向、径向分别放大1.1、1.13、1.15，切向未产生放大效果。位移峰值具有相似的变化规律。

3)应力峰值出现在台阶内侧，而质点振速峰值出现在台阶外缘，应力与振速峰值并非在同一位置出现，岩体边坡的稳定性应综合考虑振速峰值大小及应力是否超过岩体的抗拉强度来判断。