一种基于模糊聚类模型的动量轮健康性排序方法
2020-06-24季业崔振王雪涛严嵘刘一帆
季业,崔振,*,王雪涛,严嵘,刘一帆
1. 北京控制工程研究所,北京 100094 2. 空间智能控制技术重点实验室,北京 100094 3. 北京空间飞行器总体设计部,北京 100094
通常意义上能够产生一定角动量的执行机构都可以称作动量轮,比较简单且常用的是反作用动量轮(RW)和偏置动量轮(MW),在已发射的、以动量轮为执行机构的卫星中,这两种动量轮的使用占绝大多数。动量轮使用电机控制动量轮加减速,由此产生控制力矩。根据其产生的力矩不同,可以将动量轮按照力矩大小进行分类,如:10 N·m·s动量轮、25 N·m·s动量轮、50 N·m·s动量轮等。现如今,我国50 N·m·s动量轮已成熟应用于多个型号卫星并积累了大量的试验数据。从数据统计角度看,动量轮是GNC系统中故障发生率最高的部件之一。动量轮故障诊断方法的相关研究很多,主要分为两大类,一类是基于模型的故障诊断;另一类是基于数据驱动的故障诊断。国内外许多学者都对动量轮故障诊断提出了自己的方案。文献[1]用贝叶斯方法对动量轮进行可靠性建模与评估。文献[2]建立故障与征兆之间的关联矩阵后,给出动量轮故障可诊断性的评价结果。文献[3]提出未知输入扩展卡尔曼滤波,并将其应用于航天器动量轮的早期渐变型故障检测。文献[4]提出了基于Elman神经网络的卫星群姿态控制系统的故障诊断方案,并以反作用飞轮为研究对象进行故障分析和仿真试验。文献[5]通过基于BP神经网络的故障诊断方法完成对卫星动量轮的故障诊断。文献[6]对飞轮开环系统以及其内部干扰进行了精确建模,在假设系统外扰相对故障是小量可忽略的情况下,利用ESO对飞轮故障的估计直接进行了故障检测。在基于数据的动量轮故障预测中,现有文献与试验设计大多采用开环模式且动量轮工作在固定转速,不引入闭环反馈的数据样本。这种诊断法虽然便于设计试验但与真实工程应用中动量轮的工作状态或取得的实时数据仍有一定偏差。本文采集闭环动态瞬时工况电机电流,将其按工况分类并通过模糊聚类算法,得到一种动量轮健康性排序方法,应用于动量轮的健康性预测,为动量轮提供全方位监测和提前预警。
1 健康性排序方法数学模型
从动量轮整机装机到动量轮在轨运行后退役的整个生命周期,选取系统闭环工况的动量轮为研究对象,在这一过程中截取动量轮电机电流值记为:
(1)
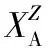
(2)
(3)
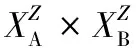
(4)
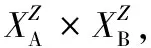
有了上述模糊聚类基础后进行试验设计。
xi={xi1,xi2,xi3,…,xn},i=1,2,…,m
(5)
于是得到原始数据矩阵为:
(6)
由于所取数值均为单一物理量在不同时间段的表现,不涉及量纲影响,故不考虑对原始数据矩阵进行标准化处理。
第二步是建立模糊相似矩阵R,即标出衡量被分类对象间相似度的统计量rij(i=1,2,…,m;j=1,2,…,n)。这里使用相关系数法:
(7)
(8)
(9)
最后使用传递闭包法进行聚类,根据标定所得的模糊矩阵R,依次求
R→R2→R4→…→R2k=R*
(10)
(11)
式中:∨为两数取大运算(逻辑加);∧为两数取小运算(逻辑乘)。其中, 当满足Rk∘Rk=R2k时,表明Rk具有传递性,Rk就是所求的模糊等价矩阵:
(12)
基于模糊等价矩阵R*,在动态聚类图中,选取适当的“λ”由大变小,进行结果分析。λ∈[0,1],得到:
(13)
式中:
i,j=1,2,…,n
由此可确定样本的聚类结果。
2 健康性排序模型设计
2.1 模型数据采集与处理
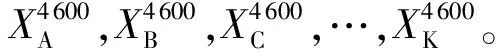
为了样本数据采集更有说服力,模型构建时设计采样方法如下:x1,x2为部件验收测试时间点数据采样;x3,x4为分系统试验测试时间点数据采样;x5,x6为AIT环境试验时间点数据采样;x7,x8为靶场试验时间点数据采样;x9,x10为在轨动量轮时间点数据采样。由于研究的目标是动量轮电机电流单一的参量,在实际应用中可以将代表性时间节点坐标提取的数量进行灵活配置。例如:可以将分系统试验测试时间点进行数据采样x3,x4,x5;也可以将在轨不同时间节点的动量轮数据进行采样x1,x2,…,x10,此作为一种拓展方法在后续试验中使用。依次处理动量轮A~K的数据,得到11组电机电流数据集合。收集原始数据如表1所示。
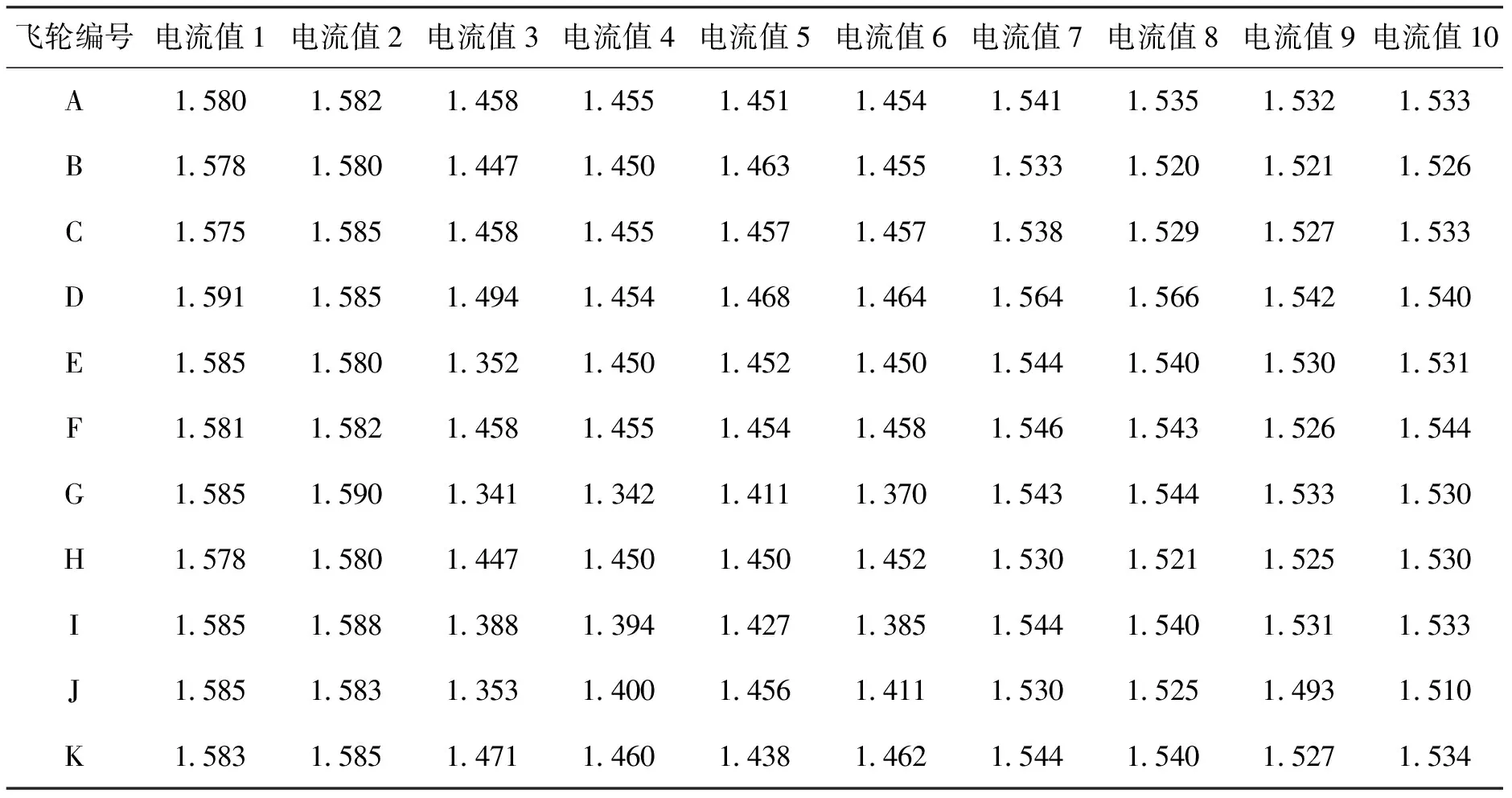
表1 原始数据1
由式(7)~式(9)得到模糊相似矩阵:
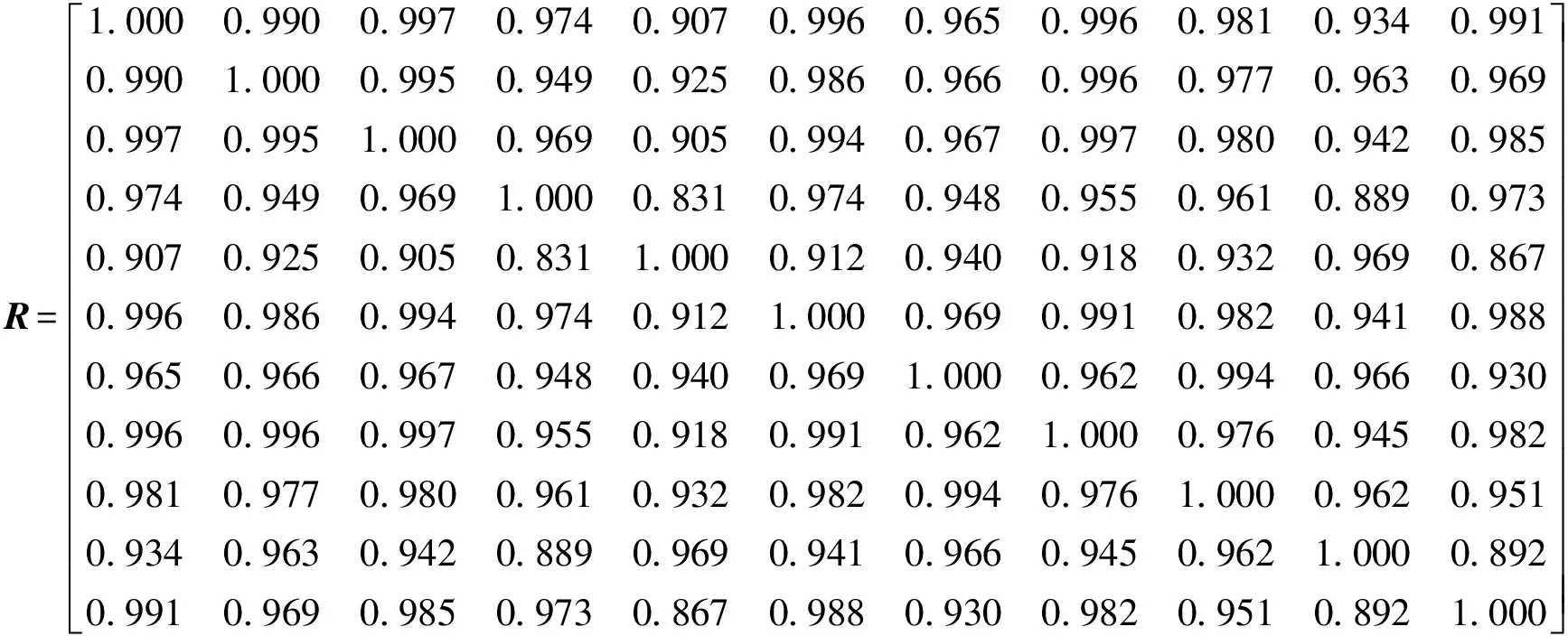
最后,由式(10)~式(12)对这个模糊相似矩阵用平方法做传递闭包运算,求R4,即t(R)=R4=R*聚类。R是对称矩阵,如下:

2.2 基本模型分析评估
选取适当的“λ”由大变小,进行结果分析。轮C和H在置信水平为0.997的阈值“λ”下相似度为1,故C/H同属一类,此时可以将样本轮子分为9类,即A/C/H;B;D;E;F;G;I;J;K。降低置信水平“λ”,对不同的“λ”作同样的分析,得到:λ=0.996时,可分为7类,即A/B/C/F/H;D;E;G;I;J;K。λ=0.982时,可分为4类。λ=0.974时,可分为3类。λ=0.966时,可分为1类,可依据此结果进行动量轮健康性排序,如图1所示。
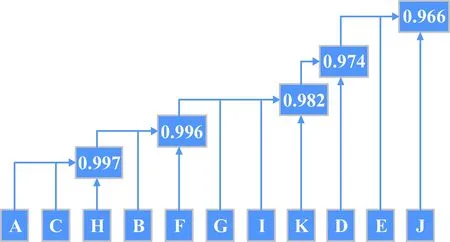
图1 健康性排序Fig.1 Health ranking
3 模型的验证
试验对象为编号L、M、 N、O共4个不同编号的动量轮组件,L、M为未发射型号动量轮(正在AIT进行试验)。N、O为已发射型号动量轮(截至发稿已在轨稳定运行8个月),编号N、O动量轮电机电流数据截取具有代表性的时间节点坐标的规则与模型构建时所述一致。针对编号L、M动量轮电机电流数据截取的时间节点坐标不满足模型构建要求的问题,设计采样方法如下:x1,x2为部件验收测试时间点数据采样;x3,x4,x5,x6为分系统试验测试时间点数据采样;x7,x8,x9,x10为AIT环境试验时间点数据采样;依照规则进行数据采样后,得到相应的4组数据,如表2所示。
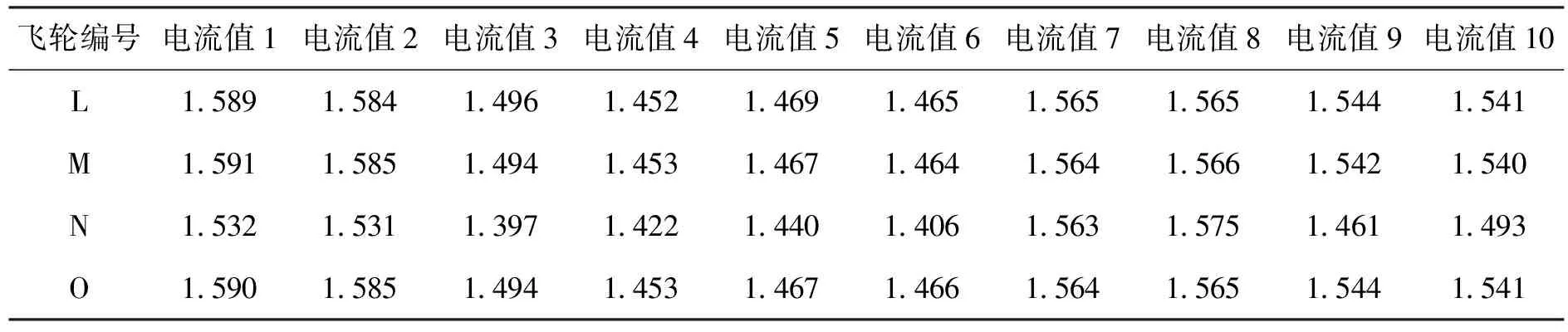
表2 原始数据2
将这4组数据依次代入模型,进行计算,结果表明:编号为L和O的2个动量轮健康性良好,依据模型在置信水平为0.996的阈值“λ”下相似度为1;编号M动量轮依据模型在置信水平为0.982的阈值“λ”下相似度为1,其健康性排序不如编号为L和O的2个动量轮。编号为N的动量轮健康性最差,刷新了原模型的置信水平,即在阈值λ=0.867情况下被单独分为一类。
2017年始,在基于振动的轴承故障诊断方面开展了系列研究,如空间轴系的微振动测试方法和评估分析方法研究。积累了一定的工程试验数据。基于振动特性的故障诊断是轴承常用的分析方法之一,其借助轴承振动信号进行数学分析,获取其峭度(Kurtosis)K是反映振动信号分布特性的数值统计量,是归一化的4阶中心矩:
(14)
式中:x为信号的振幅;E(x)为信号振幅的期望;p(x)为概率密度函数;σ为信号振幅的标准差。正常滚动轴承的振动信号幅值的概率密度分布接近正态分布。如果出现故障,就会引起冲击,进而导致振动信号中大幅值的概率密度增加,原正态分布的两边尾巴翘起,使得信号的幅值偏离正态分布函数[14-15],如图2所示。
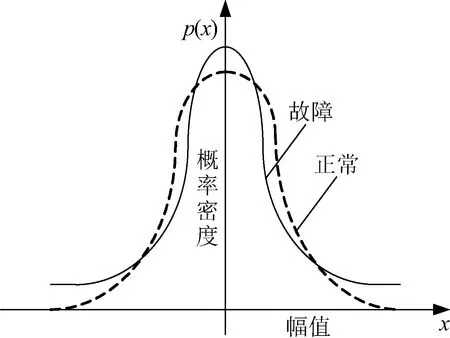
图2 振动信号概率密度分布示意Fig.2 Probability density distribution of vibration signal
峭度指标是一个重要的统计估计量。如果概率密度函数满足正态分布,则不论方差有多大,K=3。因为正常轴承的振动信号近似服从正态分布,所以其峭度值约为3。而故障轴承由于冲击信号的引入,正态分布的两边尾巴上翘如图2所示,峭度K>3;峭度越大,其损坏程度越大。峭度指标与轴承的转速、尺寸和负荷无关,与轴承精度等级、结构支撑方式、测点位置等弱相关。表3为编号A~O动量轮对应的峭度测试数据与模糊聚类排序对比。
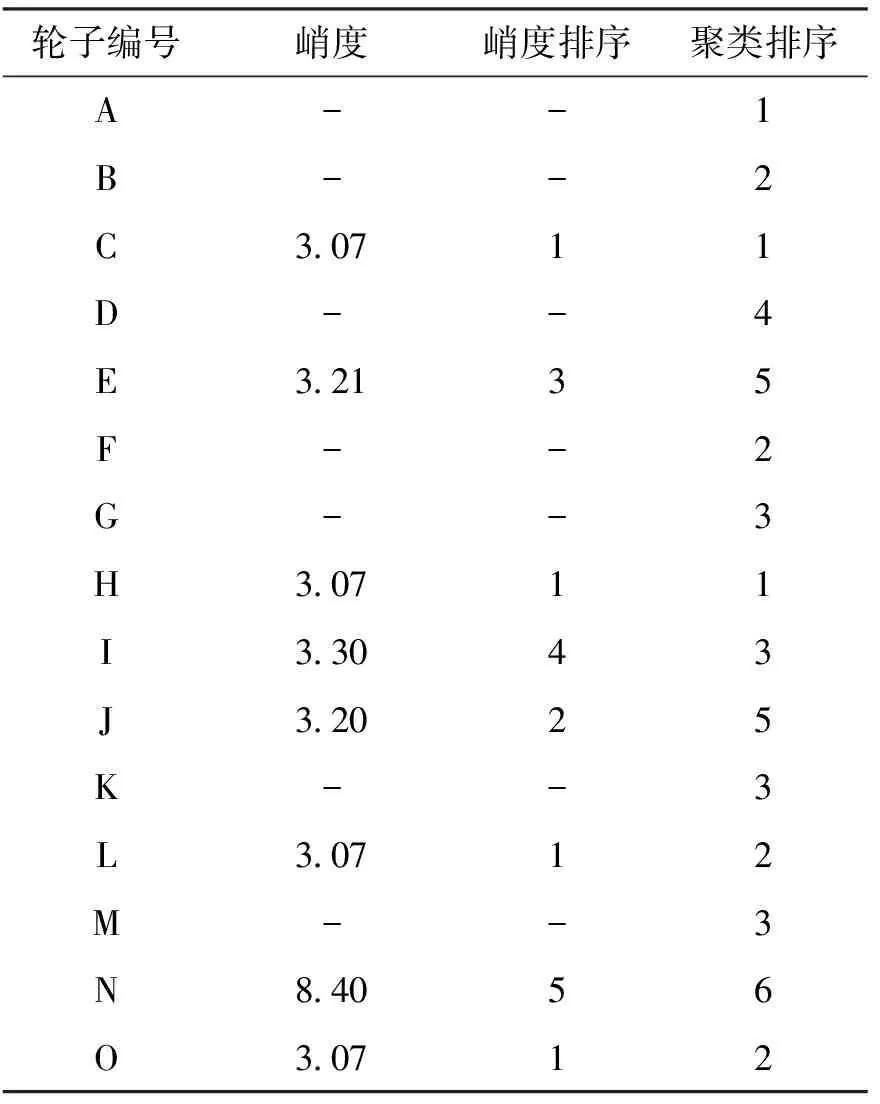
表3 两种方法比对结果
注:2017年初峭度试验开始应用于工程实践,但不是全面开展,故不是所有轮子都进行峭度试验。
依照表3可明显看出:共有8个动量轮样本进行了峭度试验,其所得K值为(3.07,8.40),依照K值进行排序,可以将动量轮分为5个级别。共有15个动量轮样本进行了模糊聚类排序,依照不同置信水平可以分为6个级别。两种方法结果都明显显示出编号为N的动量轮表现最差。峭度法显示编号C/H/L/O的4个动量轮表现最好。模糊聚类法显示编号A/C/H样本表现最好,两种方法进行对比其结果有一定相似性,但对于中间样本排序则略有不同。
4 结束语
以遥测参数为研究对象,提出了一种基于模糊聚类模型的动量轮健康性排序方法,进行试验并验证其健康性排序方法的准确性。对目前卫星动量轮的健康性排序提供了解决方案。同时,针对目前在工程中已积累的两大部分数据:卫星发射前地面测试的数据;卫星发射后的在轨数据,提供了合理的数据挖据与利用渠道。如何累计更多有效的样本数据并结合机器学习算法,推动以数据驱动的动量轮故障预测,进行模型的升级是今后研究的重点。
