基于卡尔曼滤波的汽车纵向速度滤波算法及应用

熊琦玮，彭再武，石 魏，罗宏亮，王澍龙

(1.中车时代电动汽车股份有限公司，湖南 株洲 412000； 2.长沙中车智驭新能源科技有限公司，长沙 410000)

获取准确的实时车辆纵向速度是进行相关精确控制的基础，车辆纵向速度现有的计算方法较为粗糙，其精度不高且波动大，难以作为控制器的控制输入。随着对汽车控制系统性能要求的不断提高以及智能驾驶汽车的出现，准确的纵向加速度信号在汽车上的应用越来越广泛[1]。由于加速度传感器价格从几千元到上万元不等，如果加装加速度传感器，则会大大增加车辆成本，而对车辆纵向速度进行差分可方便地得到车辆加速度[2]。因此，如何对传感器信号进行处理并获取准确的车速显得尤为重要。

本文设计了基于卡尔曼滤波的车辆速度估计，仿真与实车试验表明，与其他滤波方法相比，该方法具有良好的实时性与估计精度。

1 卡尔曼滤波的理论简介

滤波的方法最初用于信号处理领域，其作用是消除各类传感器获取信号中的随机误差，提高信号精度和准确度。因为随机信号的功率谱特性是确定并可得到相关参数的，所以要对得到的信号进行滤波，可根据有用信号和需要去除的干扰信号的功率谱设计相应的滤波器及其参数。

R.E.Kalman于1960年发表论文提出了卡尔曼滤波器，它是一种从系统状态有关的观测量中估计出所需信号精确值的最优递推滤波算法[3-4]。由于卡尔曼滤波是仅在时域内设计的滤波器，而且存储的数据很少，所以具有很强的实时性，十分容易以计算机代码的方式实现[5-7]。在许多工程领域，如制导、雷达和通讯等工程中，卡尔曼滤波已得到了较好的应用，并衍生出了扩展卡尔曼滤波、无迹卡尔曼滤波等算法[8-12]。

由于要实现计算机代码计算，需要将系统方程离散化，假设随机线性离散系统的方程如式(1)：

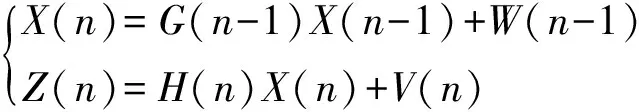
(1)

式中：X(n)为系统的状态向量；G(n-1)为系统状态的转移矩阵；W(n-1)为系统噪声；Z(n)为系统的观测向量；H(n)为系统的观测矩阵；V(n)为系统的观测噪声或测量噪声。

W(n-1)和V(n)为概率密度函数服从正态分布的高斯噪声，且满足式(2)和式(3)：

Cov[W(i),W(j)]=Q(i)δ(ij)

(2)

Cov[V(i),V(j)]=R(i)δ(ij)

(3)

式中：Q和R分别为W和V的协方差矩阵。

建立随机线性离散系统的卡尔曼滤波方程可归纳为两步：

1)使用前一时刻滤波器的输出进行当前时刻的系统状态的预测(时间更新)。

系统状态的一步预测：

X(n|n-1)=G(n-1)X(n-1)

(4)

系统状态的一步预测误差方差矩阵：

P(n|n-1)=G(n-1)P(n-1|n-1)G(n-1)T+Q

(5)

2)在得到当前时刻状态的测量值(信号原始数据)后对时间更新中得到的当前状态预测值进行修正，得到系统当前时刻的状态估计值(观测更新)。

只需给出初值X(0|0)和P(0|0)，即可根据当前时刻的系统观测值和前一时刻的预测值得到当前时刻的系统状态估计值。

增益矩阵Kg：

Kg(n)=P(n|n-1)H(n)T[H(n)P(n|n-1)
H(n)T+R]-1

(6)

系统状态估计：

X(n|n)=
X(n|n-1)+Kg(n)[Z(n)-H(n)X(n|n-1)]

(7)

系统状态估计误差方差矩阵：

P(n|n)=[1-Kg(n)H(n)]P(n|n-1)

(8)

因为式(4)～式(8)是在时域内的递推，所以非常容易以计算机代码的方式实现，流程如图1所示。

图1 卡尔曼滤波流程图

2 车辆纵向速度的卡尔曼滤波应用

2.1 滤波器设计方案

在Matlab-Simulink环境中利用Kalman Filter工具箱方便地设计卡尔曼滤波器。在本文卡尔曼滤波器设计中，式(1)中的状态向量X、观测向量Z均为车速S，因此系统观测矩阵H为1。由于实际采样频率为100 Hz，采样周期较短，可以近似认为车速在此时间内保持不变，即：

S(n)=S(n-1)

(9)

式中：S(n)为n时刻车速值；S(n-1)为n时刻的前一时刻的车速值。

同时将式(1)中的系统状态转移矩阵G取1，并取系统噪声W为0.01，系统观测噪声V为1。为了验证设计的卡尔曼滤波器的性能，与下列两种滤波算法进行比较：

1) 加权平均法。

(10)

式中：S(n)为n时刻车速估计值；s(n)为n时刻原始车速信号；s(n-i)为n时刻的前i时刻的原始车速信号。

2) 巴特沃斯IIR低通滤波。在Matlab-Simulink中利用FDA Tool工具箱设计4阶巴特沃斯IIR低通滤波器，取截止频率为1 Hz。

2.2 仿真分析

在Simulink环境中生成幅值为10无量纲的正弦信号，为模拟真实信号，加入方差为1的随机值作为白噪声，如图2(a)所示。不同的滤波方法对加入噪声的信号滤波仿真结果如图2(b)所示。

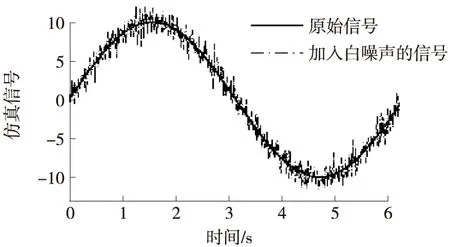
(a) 仿真信号

(b) 滤波结果对比

由仿真结果看出，采用“加权平均法”处理后的结果仍有较大误差，精度不高；“巴特沃斯低通滤波”和“卡尔曼滤波”处理后的结果曲线较为平滑，但“巴特沃斯低通滤波”处理后的结果出现了时域上较大的延迟。

2.3 实车试验

将以上3种算法自动生成C代码，烧写进整车控制器进行实车试验，结果如图3所示。

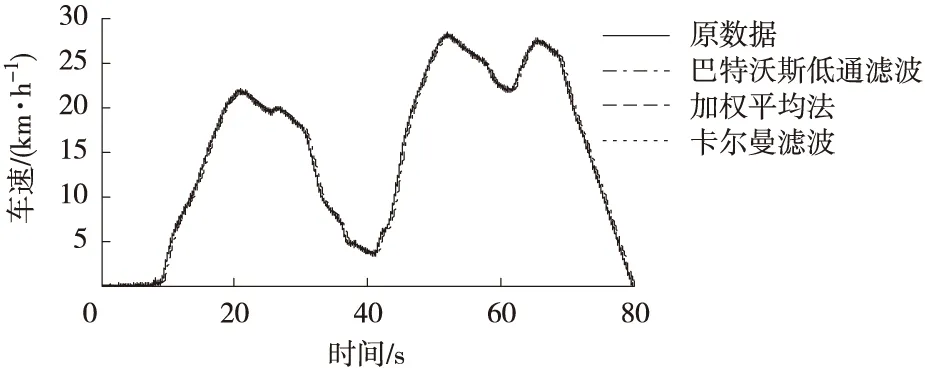
(a) 实车试验结果

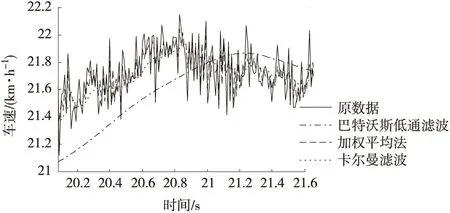
(b) 实车试验结果部分放大显示

实车试验结果表明，“巴特沃斯低通滤波”的时域延迟仍较大，“加权平均法”处理后的结果仍有较大波动，“卡尔曼滤波器”处理后的结果时域延迟较低且比较平滑。

继续通过快速傅里叶变换对数据进行频谱分析，结果如图4所示。

图4 滤波结果频域分析

由图4可知，“加权平均法”对40 Hz以上信号滤波不明显，“巴特沃斯低通滤波”优于“加权平均法”，但其信号幅值仍大于“卡尔曼滤波”。综合时域和频域表现，“卡尔曼滤波”在3种算法中性能最优。

3 结束语

通过对原始车速值进行不同算法的滤波处理，得到了车辆速度估计值。仿真和实车试验表明，卡尔曼滤波方法具有良好的实时性与较高的精度，为提高控制系统的准确度提供了可靠的保证。