机器人无标定手眼协调方法研究
2020-06-22盛荣孙首群焦玉格
盛荣 孙首群 焦玉格


摘 要:无标定情况下的视觉定位是机器人视觉伺服领域的热点和难点。提出一种基于快速自适应滤波的机器人无标定手眼协调方法。首先根据机器人三维基坐标建立运动空间和图像特征空间的微分映射关系,在不预先标定视觉传感器与机器人参数情况下,设计一个直接估计增益矩阵[Kk]的自适应滤波器,在线辨识图像雅可比矩阵。采用最小二乘法获得状态估计的初始值,在此基础上设计视觉控制器和计算运动控制量。在MATLAB环境下建立机器人手眼协调控制系统仿真模型,将该方法用于观测噪声统计特性未知情况下的定位反馈,并对机器人空间螺旋运动的跟踪情况进行分析。实验结果表明,该自适应滤波器能够完成不规则环境下视觉引导的追踪任务,定位效果优于常规卡尔曼滤波和Sage-Husa自适应滤波,具有较强的鲁棒性。
关键词:视觉定位;无标定手眼协调;增益矩阵;在线辨识;自适应滤波器
DOI:10. 11907/rjdk. 191933 开放科学(资源服务)标识码(OSID):
中图分类号:TP301文献标识码:A 文章编号:1672-7800(2020)005-0023-06
0 引言
无标定手眼协调是一个具有未建模动态的非线性系统控制问题,利用图像雅可比矩阵模型描述机器人手眼映射关系是目前最为广泛的一类方法。在机器人运动过程中,由于手眼关系的非线性,图像雅可比矩阵变化十分明显,能否在线获得有效的图像雅可比矩阵估计直接关乎机器人控制性能好坏。钱江等[1]提出了一种基于卡尔曼滤波算法的雅可比矩阵在线辨识策略,将雅可比矩阵的在线估计转化为相应系统的状态观测问题。该算法缺点是需在噪声方差阵[Q]和观测噪声方差阵[R]等模型参数已知的前提下进行;辛菁等[2]尝试对系统噪声进行实时估计,将Sage-Husa自适应卡尔曼滤波应用于在线辨识图像雅可比矩阵,实现机器人在噪声统计特性不完全已知情况下的视觉定位。但仿真实验表明,该模型对[Q]和[R]同时估计会引起滤波发散;付梦印等[3]在有关导航系统研究中介绍了一种相关自适应滤波方法,利用观测向量的相关性直接对增益矩阵[Kk]进行自适应估计。但这种方法涉及到非线性矩阵方程求解,计算复杂,实时性难以满足要求。在过程噪声和观测噪声为零均值高斯白噪声前提下,Arasaratnam[4]提出了容积卡尔曼滤波(cubature Kalman filter,CKF)。该方法通过构造一组在个数、权系数和空间位置方面确定的“容积点”进行滤波,避免了Jacobian 矩阵求解,且無需可调参数;钱华明等[5]采用该方法进行大方位失准角初始对准,用降维算法优化了采样点数,使计算时间减少了[1/3];程杨等[6]提出基于5阶相径容积规则的CKF算法,该算法采用多项式积分实现高斯积分近似;黄湘远等[7]在此基础上利用5阶CKF对大失准角情况下的非线性初始对准工作进行研究,并通过平方根法增强滤波稳定性;Bhaumik[8]在CKF基础上结合高斯—拉盖尔积分准则,提出了容积求积卡尔曼滤波(cubature quadrature Kalman filter,CQKF)方法。该方法通过构造一组高阶采样点进行滤波,使滤波精度得到进一步提高,但此方法降低了滤波实时性;徐定杰等[9]运用最小化代价函数计算渐消因子,提升了噪声干扰下的滤波精度,但是在估计误差较大的情况下会导致滤波收敛缓慢,影响应用效率。为进一步实现机器人在噪声统计特性未知情况下的实时视觉反馈和空间三维运动跟踪,本文提出一种基于快速自适应滤波的机器人无标定手眼协调方法,改善了图像雅可比矩阵辨识在不规则环境中的鲁棒性和实时性,仿真结果表明该方法有效。
1 图像雅克比矩阵在线辨识原理
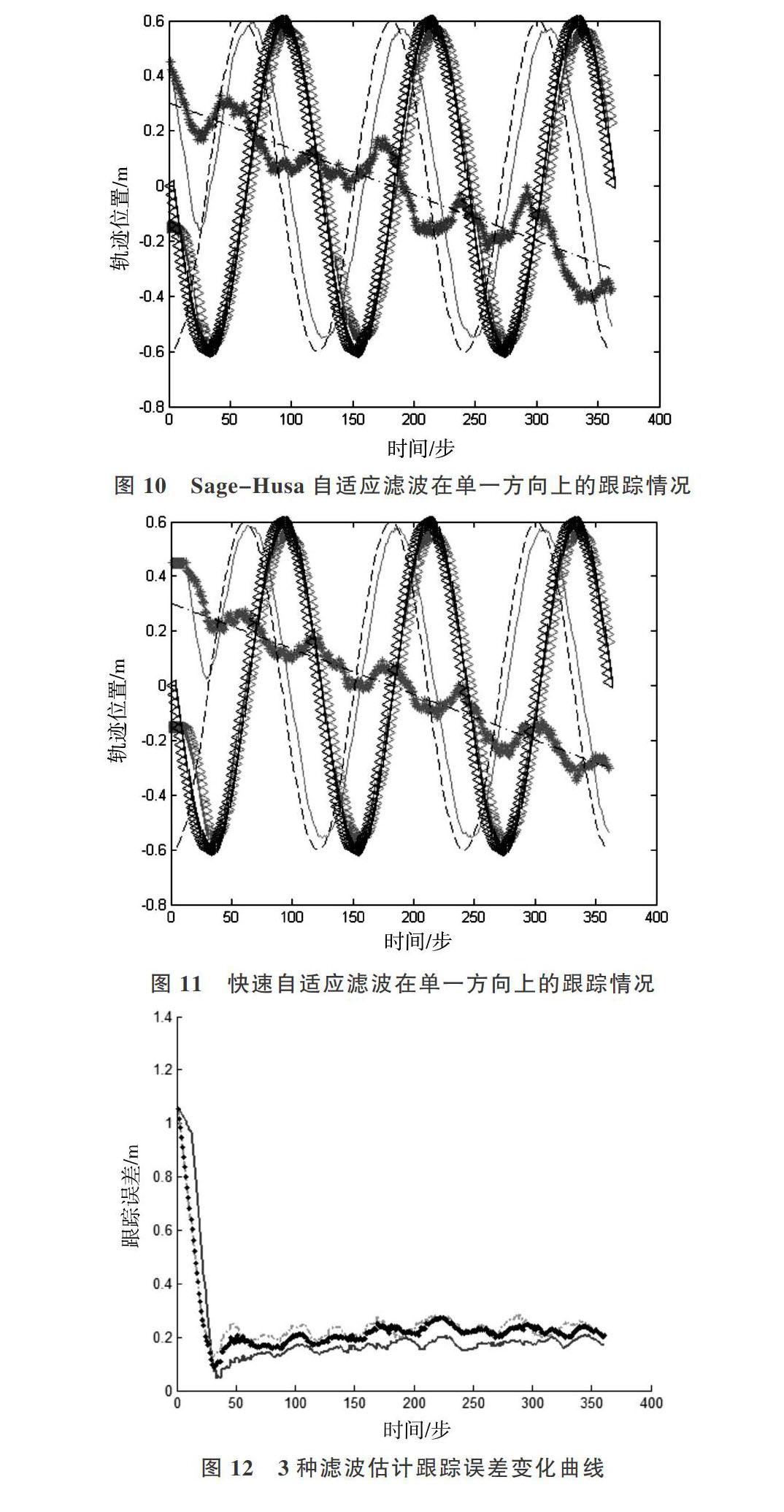
定义机器人三维基坐标系为机器人的运动空间,机械人末端执行器在运动空间的坐标为[pg=(pgx pgy pgz)T],而执行器在固定双目摄像机的坐标系内,坐标为[pc1=(pc1x pc1y ][pc1z)T]和[pc2=(pc2x pc2y pc2z)T],图像特征空间即末端执行器在双目摄像机中的图像坐标为[fg=(fg1 fg2 fg3 fg4)]=[(ug1 vg1 ug2 ][vg2])。图像雅可比矩阵不是常定矩阵[10],反映了机器人运动空间和图像特征空间的微分映射关系,其定义如下:
图像特征空间维数[m=4],大于机器人运动空间维数[n=3],可以唯一确定相应的空间位置。将手眼关系描述为图像雅可比矩阵,实际上就是将一个静态非线性系统近似为一个时变的线性系统,对雅可比矩阵的辨识就是对此线性时变系统参数的辨识[11]。
控制系统以待估的雅可比矩阵为系统状态变量。使用卡尔曼滤波算法对系统状态进行观测,可以滤去外界噪声对雅可比矩阵的干扰,使系统具有足够的鲁棒性,精度高、计算复杂度低 [12],尤其在状态估计[13]、目标跟踪[14]、导航制导[15]、机械控制[16]等领域得到广泛应用。实际情况中机器人的目标往往是随机多变的,在未知动态的机器人视觉定位系统中,基于自适应卡尔曼滤波的图像雅可比矩阵辨识模型主要存在两种噪声干扰:①由于机器人视觉系统成像模型发生改变而引发的过程噪声[η(k)];②由于图像采集与处理带来的测量噪声[v(k)][17]。卡尔曼滤波算法在过程噪声方差阵Q和测量噪声方差阵R均未知的情况下,很难得到系统精确的数学模型和噪声统计特性,对噪声方差阵和测量噪声方差阵同时估计会使滤波精度降低,甚至产生滤波发散现象,降低滤波器性能[18]。为此,本文绕过常规卡尔曼滤波必须已知系统噪声方差阵[Q]和观测噪声方差阵[R],设计一个直接估计增益矩阵[Kk]的自适应滤波器在线辨识图像雅可比矩阵。
然后使用[j(0)]构成[x(0)]。在整个递推估计过程中只需在系统初始时给出 3步试探运动,此后的雅可比矩阵将充分利用已完成的跟踪运动信息进行自适应滤波递推估计,无需再引入任何试探运动。
2 视觉控制器设计
全局视觉的目的是引导机器人末端大范围跟踪目标运动,建立最优反馈控制。
3 实验与结果分析
为验证本文提出的基于快速自适应滤波算法在机器人无标定手眼协调中的有效性,在MATLAB环境下建立机器人手眼协调模型。在随机噪声环境下,基于机器人空间视觉引导进行末端轨迹跟踪实验。
3.1 实验设计
仿真条件:在MATLAB平台上完成,使用机器人和机器视觉工具箱,建立机器人手眼协调控制系统仿真模型,图1为控制系统结构。设双目摄像机在机器人三维基坐标系中(3,0.5,0和3,0.5,0,单位为[m])镜头分别与[Y]轴呈[π/12]和[-π/12]的夹角。双目摄像机焦距[f1=f2=0.015m],显示的图像平面分辨率为1 024×1 024,像素尺寸为[10-5×][10-5m/pixel]。
机器人采用工具箱中提供的PUMA560型六自由度关节式机器人,其连杆参数如表1所示,运动范围为以肩部中心为球心、0.92[m]为半径的空间半球。PUMA560型机器人的6个关节都是转动关节,前3个关节确定手腕参考点位置,后3个关节用于确定手腕方位[20]。设置机器人末端[x、y、z]轴3个方向的最大移动速度均不超过[0.9m/s]。
在系统配置完全相同的情况下,动态目标作空间螺旋线运动,向双目摄像机依次加入均值为0、最大幅值为[±3和±6]像素的随机噪声,然后比较常规卡尔曼滤波、Sege-Husa实时估计观测噪声滤波和快速自适应滤波为核心的3种手眼协调控制方法的跟踪性能,以验证本文提出的基于快速自适应滤波的机器人无标定手眼协调控制方法的有效性。
首先使用本文的手眼协调控制方法跟踪上述空间螺旋线运动。图2为MATLAB环境下的机器人手眼协调控制系统仿真模型(彩图扫描OSID码可见,下文同),图3为机器人对直线运动的跟踪情况,图4显示跟踪运动完成时刻PUMA560机器人的位姿,图中3个分散点为跟踪开始前的3步试探运动,图5为使用快速自适应滤波算法得到的机器人跟踪轨迹,图6和图7是双目摄像头跟踪过程中捕捉到的目标小球和机器人末端图像坐标点集合。图2-图7显示,基于快速自适应滤波的手眼协调控制方法能实现机器人对空间运动的跟踪。
3.2 实验结果
为进一步说明本文方法的跟踪性能,在噪声相同的情况下比较螺旋运动跟踪过程中,3种滤波估计算法所形成的机器人末端与目标小球之间的空间距离变化。
图8是随机噪声为[±3]像素、均值为0时,机器人分别使用3种滤波估计方法产生的跟踪误差变化曲线(绿色、蓝色、红色散点分别代表常规卡尔曼滤波、Sage-Husa自适应滤波、快速自适应滤波),在噪声和摄像机参数完全相同的情况下,PUMA560机器人根据3种滤波算法估计的图像雅可比矩阵进行跟踪所产生的效果差距明显。使用常规卡尔曼滤波接近目标(位置误差趋于0)所用帧数最少,Sage-Husa自适应滤波算法次之,而快速自适应滤波算法开始跟踪前需要收集12帧目标运动信息,故接近动态目标所用时间最长。表2是3种滤波算法的每帧平均滤波时长,常规卡尔曼滤波耗时最短,快速自适应滤波由于最初的12帧追踪速度较慢,导致平均时长最长,是常规卡尔曼滤波的两倍左右;Sage-Husa自适应滤波与常规卡尔曼滤波的平均耗时相近,都在3ms左右。在第50帧前,3种控制方法都完成了追赶动态目标任务。为了使之后的持续跟踪产生显著差异,本文选取[±6]像素、均值为0的随机噪声。下面比较3种滤波估计算法下,机器人相对目标曲线在[x、y、z]轴单一方向上的跟踪情况,以及机器人跟踪曲线与目标曲线空间位置上的误差变化。
图9至图11显示了在[±6]像素、均值为0的随机噪声下,3种滤波估计在单一方向上对动态目标的跟踪情况。3种滤波估计都能有效追踪目标,前50帧内3种估计方法误差都比较大,常规卡尔曼滤波和Sage-Husa自适应滤波在第30帧前后误差趋于稳定,快速自适应滤波在40帧后的追踪轨迹与实际目标轨迹重合度较大(跟踪误差最小)。图12是3种滤波估计方法产生的跟踪误差变化曲线。常规卡尔曼滤波受固定的过程噪声和观测噪声方差影响,跟踪误差变化幅值最大,动态目标每旋转一周即沿轴线移动一个导程,跟踪误差就会达到一个峰值,最高峰值甚至超过了0.3m;Sage-Husa自适应滤波算法因为可以实时估计对系统影响较大的观测噪声,跟踪误差变化的幅度小于常规卡尔曼滤波,其在第200~250步之间的峰值最高,与常规卡尔曼滤波峰值相近,Sage-Husa自适应滤波算法的峰值平均在0.2m左右;使用快速自适应滤波算法的跟踪过程显然优于前两者,50帧后的跟踪误差较为平稳,误差的波峰與波谷变化幅度在0.1m以内,3个导程范围内产生了6个峰值,最高峰值低于0.2m,平均峰值0.15m左右。
4 结语
本文针对机器人在无标定手眼协调中对视觉反馈较高的鲁棒性要求,提出一种基于快速自适应滤波的机器人无标定手眼协调方法。该方法通过建立自适应卡尔曼滤波递推估计和最优反馈控制,设计一个直接估计增益矩阵[Kk]的自适应滤波器在线辨识图像雅可比矩阵,实现了对噪声统计特性未知情况下的实时视觉反馈和空间三维运动跟踪。通过MATLABR实验平台进行仿真实验,对机器人无标定手眼协调下的定位方法研究成果如下:
(1)快速自适应滤波算法能实现对图像雅克比矩阵的在线辨识,无需预先知道噪声的统计特性和视觉传感器详细参数,且可忽略噪声模型误差带来的影响,对提高图像雅克比矩阵的辨识精度有重要意义。
(2)仿真结果表明本文算法滤波精度优于常规卡尔曼滤波和Sage-Husa自适应滤波。由于快速自适应滤波需要收集12帧目标运动信息,所以接近动态目标所用时间最长。但是在第50帧之后,3种滤波算法误差趋于稳定,不影响整体的滤波估计。结果表明本文设计的快速自适应滤波器可在噪声特性未知的情况下提高视觉反馈系统鲁棒性。
本文的不足之处是未详细讨论快速自适应滤波算法滤波速度较慢的原因,关于前12帧信息收集时间对整个滤波过程的影响情况未深入探讨。
参考文献:
[1] 钱江. 基于图象雅克比矩阵的无标定手眼协调[D]. 上海:上海交通大学, 2003.
[2] 辛菁,白蕾,刘丁. 基于自适应Kalman滤波的机器人6DOF无标定视觉定位[J]. 系统仿真学报,2014,26(3):586-591.
[3] 付梦印,肖烜,邓志红,等. 陆用惯性导航技术[M]. 北京:科学出版社,2017:1-63.
[4] ARASARATNAM I,HAYKIN S. Cubature kalman filters[J]. IEEE Transactions on Automatic Control,2009,54(6):1254-1269.
[5] 钱华明,黄蔚,孙龙. 基于改进的迭代容积卡尔曼滤波姿态估计[J]. 哈尔滨工业大学学报,2014,46(6):116-122.
[6] BHAUMIK S, SWATI. Cubature quadrature kalman filter[J]. IET Signal Process,2013,7(7): 533-541.
[7] JIA B,XIN M,CHENG Y. High-degree cubature kalman filter[J]. Automatica,2013,49(2):510-518
[8] 黄湘远,汤霞清,武萌. 5阶CFK在捷联惯导非线性对准中的应用研究[J]. 系统工程与电子技术,2015,37(3):633-638.
[9] 徐定杰,沈忱,沈峰. 时变有色观测噪声下基于变分贝叶斯学的自适应卡尔曼滤波[J]. 电子与信息学报,2013,35(7):1593-1598.
[10] 徐波,王金生,徐洲石. 智能巡检机器人调度与路线规划能力[J]. 长春工业大学学报,2016,37(3):269-272.
[11] 秦伟洋,岳晓峰,吴焕新,等. 机器人无标定手眼协调系统视觉跟踪[J]. 长春工业大学学报,2018,39(3):233-237.
[12] DUNIK J,SIMANDL M,STRAKA O. Unscented kalman filter: aspects and adaptive setting of scaling parameter [J]. IEEE Transactions on Automatic Control,2012,57(9):2411-2416.
[13] GUSTAFDDON F, HENDEBY G. Some relations between extended and unscented and unscented Kalman filters[J]. IEEE Transactions on Signal Processing,2012,60(2):545-555.
[14] 蒋恩松,李孟超,孙刘杰. 一种基于神经网络的卡尔曼滤波改进方法[J]. 电子与信息学报,2007,29(9):2073-2076.
[15] 徐定杰,贺锐,沈峰,等. 基于新息协方差的自适应渐消卡尔曼滤波器[J]. 系统工程与电子技术,2014,36(7):1405-1409
[16] 李理敏,龚文斌,刘会杰. 基于自适应扩展卡尔曼滤波的载波跟踪算法[J]. 航空学报,2013,33(7):1319-1328.
[17] 周飞菲. 噪声统计特性失配的魯棒目标跟踪方法[J]. 电子测量与仪器学报,2018,32(9):195-201.
[18] ARULAMPALAM M S,MASKELL S,GORDON N,et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing,2002,50(2):174-188.
[19] 张宪霞. 基于SPSA优化的Kalman滤波无标定视觉伺服[J]. 系统仿真学报,2018,30(12):4754-4759.
[20] 李辉,李开世,黄文权. 基于MATLAB与ADAMS的PUMA560机器人逆运动仿真[J]. 机械工程师,2014(11):105-106.
(责任编辑:杜能钢)
