基于局部线性嵌入算法的SSVEP脑机接口系统研究

刘福伟 童基均 李琳

摘 要：提出一个多频率刺激源诱发的稳态视觉诱发电位（SSVEP）脑—机接口系统，针对时域脑电信号特征维数过多等问题，采用一种局部线性嵌入算法（LLE）对经过预处理的脑电数据进行降维。实验结果表明，随着分析时间窗的增大，经典功率谱密度分析（PSDA）与典型相关分析（CCA）等方法相比，基于LLE的非线性数据降维方法具有一定优势。当时间窗为1.65s时，其分类准确率达92.92%，信息传输率达59.62 bits/min，远远优于其它方法。

关键词：脑—机接口;稳态视觉诱发电位;局部线性嵌入算法

DOI：10. 11907/rjdk. 191831 开放科学（资源服务）标识码（OSID）：

中图分类号：TP303文献标识码：A 文章编号：1672-7800（2020）005-0014-05

0 引言

脑机接口被称为大脑端口或者脑机融合感知，是动物大脑与外部设备建立的直接连接通路[1]。脑机接口技术（Brain-Computer Interfaces，BCI）是一种涉及神经科学？、信号检测、信号处理？、模式识别等多学科的交叉技术，是一种新型的人机交互技术，它通过不间断地监控大脑活动中与人意图相关的脑部信息实现与外部交流[2-3]，实现了人类思维对外部设备的直接控制。目前，可用于BCI的人脑信号主要有：脑磁图（Magnetoencephalogram，MEG）、脑电图（Electroencephalography，EEG）和功能性核磁共振图像（Functional Magnetic Resonance Imaging，FMRI）[4]。EEG技术由于安全、成本较低等优点，其在BCI的研究中应用最为广泛[5]。

诱发电位也称诱发反应，是指给神经系统某一部位特定刺激，相应部位产生的生物电反应[6]。目前，诱发电位方式主要分为视觉诱发电位、听觉诱发电位和机体觉诱发电位[7-8]。而稳态视觉诱发电位（Steady State Visual Evoked Potential，SSVEP）是指以大于6HZ频率的闪光刺激眼睛视网膜时，大脑信号调制同时产生的节律性周期，其表现在EEG上是在对应刺激频率或其谐波上出现谱峰[9-10]。换言之，稳态视觉诱发电位（Steady State Visual Evoked Potential，SSVEP）是视觉部分对于高频率刺激的物理反应，其具有明显的特征信号、节律同化和周期性现象，而且信号噪声比其它方式大[11-12]。由于SSVEP具有更高的信息传输率、系统和实验设计更加简便以及需要训练的次数少等优点[13]，因此许多脑电研究者将SSVEP应用于脑机接口系统中。

功率谱密度分析（Power Spectral-Density Analysis， PSDA）和典型相关分析法（Canonical Correlation Analysis，CCA）是目前SSVEP脑机接口系统中传统频率识别方法[14-15]。为了分析功率谱信息，PSDA通过傅里叶变换将原始信号从时域变换到频域[16]。CCA是研究两组变量相关关系的一种统计方法，这种方法相较于快速傅里叶变换的谱估方法无论时间长短，其都具有更强的抗噪性[17]。但是CCA不能完全构建出真实的电信号成分，导致提取效果不太理想，针对此问题，研究者大都热衷于研究改进的CCA算法[18]。1996年，Tibshirani等[19]提出一种尝试寻找稀疏解的最小绝对收缩和选择算子（Least Absolute Shrinkage and Selection Operator，LASSO），其被首次运用于解决SSVEP的识别问题。这种算法比原始CCA具有更高的信息传输率，缩短了识别所需时间，从而提高了基于SSVEP的脑机接口系统实时性。

1 研究方法

1.1 实验设计及数据采集

实验中使用4个LED灯作为刺激源诱发SSVEP系统。实验数据采集过程中的硬件摆放位置如图1所示，左上、右上、左下、右下分别放置一个浅绿色灯光的LED灯作为刺激源，4个LED灯对应的中频段分别是13Hz、15Hz、17Hz、19Hz。

实验开始时，显示器屏幕左下方深蓝色小方块上的白色箭头提示将要移动的方向，之后屏幕上对应方向的绿色小方块变紫色，并发出蜂鸣声，显示器外侧的LED灯在两秒后开始闪烁，持续时长为4s。

本实验共有9名受试者，其中女性2位，男性7位。受试者视力均正常，年龄在22.4+3.1，受试者没有精神方面的疾病且没有家族遗传史。在实验过程中受试者不能有眨眼睛、移动、点头等动作，要专心致志地注视LED灯，若在此过程中受试者有任何不适则立即停止实验。

本实验信号的采集设备为GES400，实验环境：安静、舒适;实验地点：脑电信号研究实验室。32个电极按照国际10-20标准放置，如图2所示。头皮与导联电极之间的偏置电压设置为50V以下，采样频率为2 048Hz。

1.2 数据预处理

因实验环境问题在实验过程中不可避免产生一些误差噪声而影响实验结果。为解决此问题，需对原始脑电信号进行预处理。

高频脑电信号在传播过程中会受到颅骨抑制，造成SSVEP的能量只处于前期，因此本实验的SSVEP能量只能从前3次的谐波中获取，如图3（a）所示。为了去除后期无用的频率段，本实验首先使用一个4阶带通为12～60 Hz的巴特沃斯滤波器滤除噪声和直流漂移等频段，然后使用公共平均参考法做电极参考，进而除去脑部公共活动成分。公共参考法如式（1）。

1.3 空间滤波

数据预处理可有效解决系统误差对实验结果造成的影响，但是获取的脑电信号较为微弱、能量不集中[20]，其对噪音比的增强受到限制。因此，对预处理后的数据還需通过空间滤波增强噪音。关于空间滤波的研究较多，但这些方法应用在多频率的SSVEP滤波上存在很多不足。例如PCA是建立在完全无关基础上选择最大值作为空间滤波器，但SSVEP信号与其它脑电信号具有一定关联;共空间模式的原理是利用矩阵对角化，找到最优的空间滤波器进行投影，使两类信号差异最大化，从而增强信噪比，但是共空间模式需事先构造刺激和非刺激脑电片段，过程较为繁琐;ICA方法需事先知道频率才能选择滤波器。结合各种因素和情况，使用电极选择和简单加权融合方法虽没有达到预期最佳效果，但适用性非常广，没有必要根据个体差异分别选择空间滤波器。最常用的空间融合方法是拉普拉斯融合，其原理是使用式（3）的加权系数计算中间电极信号与周围同距电极信号的差，去除局部共同噪声达到增强SSVEP信噪比的目的。

1.4 局部线性嵌入算法

2000年，Roweis&Sa[21]提出了一种局部线性嵌入算法（Locally Linear Embedding，LLE），该算法主要针对非线性信号的优化问题，通过线性逼近全局，将高维空间映射到低维空间，通过观察小区域里点与点之间的关系，提取嵌入在高维空间里的低维子空间。

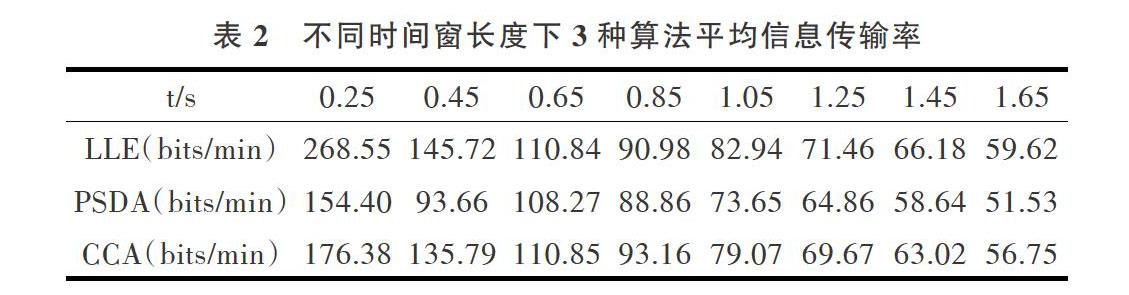
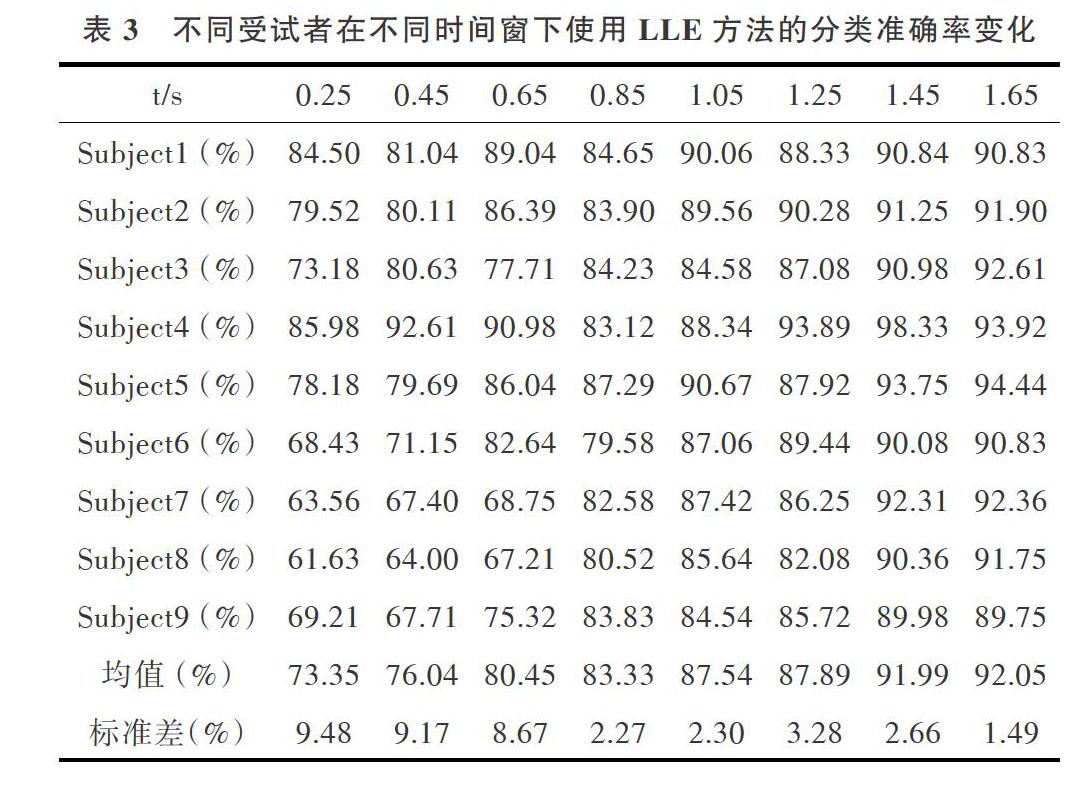
LLE算法是将数据集[X={x1，x2，x3，x4，？，xn}，xi∈Rd]映射到数据集[Y={y1，y2，y3，y4，？，yn}，yi∈Rm（m

Step1：局部近邻点选取。对于上文提到的数据集[X={x1，x2，x3，x4，？，xn}，xi∈Rd]在高维空间寻找每个样本点[xi]的[k][（k

将问题转换为求[M]的[m]个最小非零特征值[Y]对应的特征向量问题，从小到大对[M]的特征值进行排序，一般情况下[M]的最小特征值都接近于零，因此取第2到[m+1]之间的特征值所对应的特征向量组成列向量，作为[N？m]（假设有[N]个数据点）的数据表达矩阵[Y]。

2 结果与分析

2.1 预处理效果

数据预处理效果如图4所示，t表示时间（单位是s），U表示电压（单位uv），图4（a）是处理前的效果，图4（b）是处理后的效果。图4（a）的脑电信号由于噪声的存在其波动幅度较大，频率较高且分布散乱，没有规律。经过处理后的图4（b）噪声被消除，其信号波动幅度和频率比较有规律，为后续实验提供了一个标准输入。

2.2 时间窗长度对分类准确率的影响

系统正确输入指令占所有输入指令的比例称为分类准确率，是脑机接口系统常用的评价指标。图5和表1是不同时间窗下PSDA、CCA和LLE三种方法的平均分类准确率。初始时间窗长度是0.25s，步长0.1，最大时间窗长度为1.6。结合图6和表1可以看出，随着时间窗长度的增加，3种方法的分类准确率都相应提升。当时间窗长度小于0.6s时，基于流形学习的非线性数据降维方法（LLE）的分类准确率最高，3种方法的平均分类准确率差异较大。当时间窗长度大于0.6s时，3种方法的平均分类准确率相差无几。在最大时间窗下平均分类准确率最高的是基于流形学习的非线性数据降维方法（LLE）。

2.3 时间窗长度对信息传输率的影响

每分钟系统传输的信息量定义为信息传输速率（Information Transfer Rate，ITR），是脑—机接口中的一个重要评价指标。ITR的定义如式（10）和式（11）所示。

其中，[N]是脑机接口可执行的指令总数，[P]为分类准确率，[V]为单位时间内执行的指令个数，每个命令被执行的概率相同。如图6所示，ITR表示信息传输率，t表示时间窗长度，图6是3种算法在不同时间窗长度下平均信息传输率变化情况。如表2所示，t表示时间窗长度，对应值为时间窗长度在增加0.2s情况下的平均信息传输率。

由图5可以看出，随着时间窗长度的增加，3种算法的分类准确率呈升高趋势，图6中随着时间窗长度的增加平均信息传输率呈下降趋势。信息传输率由时间窗长度和分类准确率共同决定，但综合图5和图6可以看出，时间窗长度对平均信息传输率的影响更大。

综合分析图6和表2可知，3种算法平均信息传输率随着时间窗长度的增加都呈现下降趋势。在时间窗长度小于0.6s时，LLE的平均信息传输率最大，CCA的平均信息传输率大于PSDA。在最短时间窗下3种算法的平均信息传输率差距最大。当时间窗长大于0.6s时，3种算法的平均信息传输率基本相同，且下降都比较缓慢。

2.4 不同个体间差异

因环境、情绪不同会导致同一个体的脑电信号变化，这种变化在不同的个体间更加突出。如表3所示，t表示时间窗长度，对应值是不同个体在时间窗长度增加0.2s情况下的分类准确率，在0.25s窗口长度下，S1和S4的分类准确率都在80%以上，S6、S7、S8、和S9都在70%以下。在时间窗长度为1.05s情况下，所有个体的分类准确率都达到了80%以上。在时间窗长度为1.65s时，除S9外，其它个体的分类准确率甚至达到了90%以上。

综合分析可知，随着时间窗长度的增加，大部分个体分类准确率都呈上升趋势，只有少数个体在某一时间窗长度下会出现下降趋势。例如，在时间窗长度为1.25s时，S1、S5、S7和S8的分类准确率比时间窗长度为1.05s情况下的分类准确率低。标准差随着时间窗长度的增加不断缩小。

不同个体同一时间窗长度下的分类准确率不同，主要是因为：一是不同个体间的心理活动和生理结构不相同;二是每个受试者的参与专注度不同。

3 结语

随着IT技术的快速发展，脑机接口技术相关研究也越来越多。以往研究中所运用的脑机接口技术都有很大缺陷，如一些技术需要经过大量训练，可能因数据不足导致训练结果不理想等。为解决此问题，出现了一些不需要训练的技术，如本实验所用的SSVEP。SSVEP具有响应强度高、诱发速度快、不需要训练等优点，但也存在脑电信号微弱、随机性强等缺点，若直接使用SSVEP信号波形作为脑—机接口输入，则无法有效识别视觉刺激频率。针对此问题，本文使用拉普拉斯融合方法，先对多通道脑电信号运用空间滤波增强信噪比，再用局部线性嵌入算法对空间滤波处理后的信号进行降维，将原始空间不可分的脑电数据投影到高维空间，使其变得线性可分，经过降维后，脑电数据特征减小，数据复杂度降低，分类准确率提升。實验结果表明，运用此方法在多频率识别的SSVEP脑—机接口系统中是可行的。在短时间窗长度下，LLE的分类准确率比CCA和PSDA的分类准确率高。综合分析可知，随着时间窗长度的增加，分类准确率呈上升趋势，但在时间窗长度达到某一特定值时，3种方法的分类准确率基本相同。在短时间窗下LLE的平均信息传输率最高，随着时间窗长度的增加，3种方法的平均信息传输率均呈下降趋势。对于离线的脑机接口系统，一般只考虑分类准确率对系统性能的影响，对于平均信息传输率一般都会忽略不计。因此，大部分研究者都会通过提高分类准确率优化和改善系统性能。真正做好一个脑机接口系统需要考虑的因素极其复杂，如系统高效性、便捷性等，应选择最佳时间窗长度，均衡其对分类准确率和平均信息传输率的影响，提高脑机接口系统性能。

参考文献：

[1] 邱诗元. 基于脑机接口的机械臂遥操作控制[D]. 广州：华南理工大学，2017.

[2] KOSMYNA N，TaARPIN-BERNARD F，RIVET B. Adding human learning in brain——computer interfaces （BCIs）[J]. ACM Transactions on Computer-Human Interaction， 2015， 22（3）：1-37.

[3] 优化思维任务模式的MI-BCI技术研究[D]. 天津：天津理工大学，2016.

[4] 基于视觉诱发电位的脑—机接口分析算法优化及实时控制系统构建[D]. 上海：华东理工大学， 2013.

[5] 杨帮华，李博. 基于脑机接口的康复训练系统[J]. 系统仿真学报， 2019，31（2）：12-18.

[6] 杨健，王昕. 诱发电位在儿科临床的应用[J]. 国际儿科学杂志，2009，36（6）：658-660.

[7] 師娟. 脑干听觉诱发电位在眩晕中的应用价值[J]. 中外医疗，2017，36（36）：96-97.

[8] 丁佳，张娟，王索刚. 基于视觉双特征的并行联合脑-机接口范式的研究[J]. 科学技术与工程， 2015， 15（10）：37-41.

[9] 郭湛超，覃玉荣，赵隆. 视觉通路下闪光刺激对SSVEP影响的仿真研究[J]. 电子测量与仪器学报，2016， 30（4）：653-659.

[10] 张振昊，张智君. 视觉稳态电位的基频和谐波对注意的响应机制[C]. 第二十届全国心理学学术会议——心理学与国民心理健康摘要集，2017.

[11] 李东阁. 不同灰度值刺激产生的稳态视觉诱发电位比较[J]. 中国医学物理学杂志， 2019（3）：340-343.

[12] FERNANDEZ-FRAGA S M，ACEVES-FERNANDEZ M A，RODRíGUEZ-RESENDíZ J， et al. Steady-state visual evoked potential （SSEVP） from EEG signal modeling based upon recurrence plots[J].  Evolving Systems， 2017，10（2）：97-109.

[13] 杨俊宇. 基于SSVEP的脑机接口系统研究与设计[D]. 南京：南京邮电大学，2015.

[14] WANG R，WEN W，IRAMINA K，et al. The combination of CCA and PSDA detection methods in a SSVEP-BCI system[C]. Shenyang：Intelligent Control & Automation，2015.

[15] 杨红粉. 频域技术应用于点云配准研究[D]. 地理信息世界，2015，22（3）：78-82.

[16] YU Z，ZHOU G，ZHAO Q，et al. Multiway canonical correlation analysis for frequency components recognition in SSVEP-based BCIs[C]. International Conference on Neural Information Processing，2011：287-295.

[17] 笪铖璐，陈志阳，黄丽亚. 基于CCA的SSVEP性能研究[J]. 计算机技术与发展， 2015（5）：52-55.

[18] 李明爱，梅意城，孙炎珺，等. 眼电伪迹自动去除方法的研究与分析[J]. 仪器仪表学报， 2014（11）：2515-2523.

[19] 王瑞敏. 基于稳态视觉诱发电位的脑机接口的研究[D]. 南京：南京理工大学，2015.

[20] 康莎莎. 多类运动想象脑电信号的识别及其在BCI中的应用[D]. 合肥：安徽大学，2016.

[21] ROWEIS S. T.Nonlinear Dimensionality reduction by locally linear embedding[J]. Science， 2000， 290（5500）：2323-2326.

（责任编辑：孙 娟）