刀具半径补偿在铣削加工中的过切研究

李丽萍

(厦门工学院 机械与制造工程学院，福建 厦门 361021)

0 引言

在复杂轮廓的铣削加工中，若根据刀具半径的大小计算刀具中心轨迹位置，运算过程不仅繁琐且易出错；当刀具磨损较严重或更换不同直径的刀具时，还需重新计算刀具中心轨迹坐标并更改相应程序。如果采用刀具半径补偿的方式进行编程和加工，只需按照零件的轮廓进行编程而不必考虑刀具半径的影响。因此，通过合理地设置刀具半径补偿的方式，可大大简化程序编写的难度，是当下数控铣削编程中最常采用的方法。

刀具半径补偿应用在各类轮廓的铣削加工中，依据理论路径，选择合适的圆弧过渡补偿，实现刀具在偏置路径上的平稳过渡[1]。但是，在实际加工中，由于各类细节问题的干涉，看似在理论上可行的方案，在实际加工中也会遭遇各种过切问题。其中，在圆弧尖角过渡的型腔加工中，过切问题更是需要通用可行的方法来解决。

1 型腔尖角圆弧过渡补偿分析

1.1 型腔尖角圆弧过渡补偿建立方法

如图1所示的铣削零件，型腔由三段半圆组成，且两段R15半圆圆弧相交过渡点为尖角，尖角过渡处容易发生过切[2]，在建立刀具半径补偿时需要重点考虑。

采用圆弧补偿法建立刀补，从左偏刀具半径补偿和右偏刀具半径补偿两种方式来看，有以下两种建立刀补的方法[3]，如图2所示。

图2(a)采用G41建立刀补，从1点出发，到2点建立刀补，逆时针加工方向；图2(b)采用G42建立刀补，从1点出发，到2点建立刀补，顺时针加工方向。

1.2 左刀补仿真加工

采用图2(a)所示的左刀补，用数控程序O0041在斯沃仿真软件FANUC 0iM数控系统进行仿真加工(采用直径10 mm的端铣刀)，仿真效果如图3(a)所示。

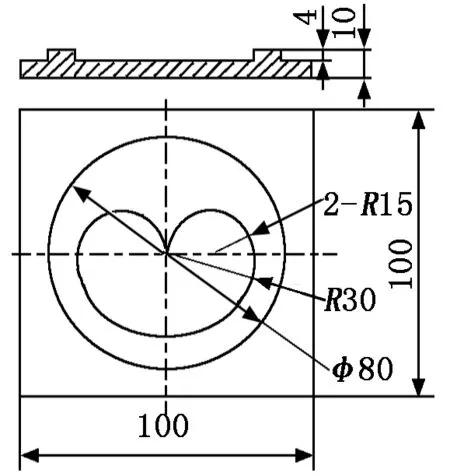
图1 铣削零件图

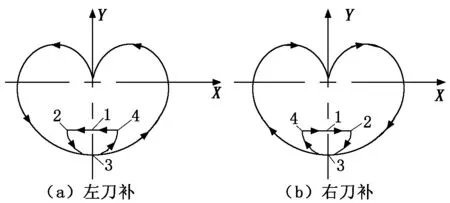
图2 圆弧过渡刀补建立方式

具体代码如下：

O0041;

N01 G54 G90 G17 G40;

N02 M03 S800;

N03 G00 X0 Y-20;

N04 Z5;

N05 G01 Z-4 F50;

N06 G41 X-10 D01 F150;

N07 G03 X0 Y-30 R10;

N08 X30 Y0 R30;

N09 X0 Y0 R15;

N10 X-30 Y0 R15;

N11 X0-30 R30;N12 X10 Y-20 R10;

N13 G40 G01 X0；

N14 G00 Z100;

N15 M05;

N16 M30;

从编程理论的角度来看，左刀补采用的补偿方式是可行的，满足刀补建立的程序段轨迹与执行刀补开始的程序段轨迹间夹角为钝角的要求，同时还满足刀补建立与刀补撤销轨迹的长度大于刀具半径值。虽然满足刀补建立的理论依据，但从图3(b)所示的测量结果可知，在圆弧尖角过渡的地方(坐标X0，Y0)发生了明显的过切。

考虑刀具直径的大小对过切存在的影响，换小直径刀具在斯沃仿真软件FANUC 0iM数控系统进行仿真加工，得到相应的仿真结果，如图4所示。

从图4可以看出，随着刀具直径的减小，过切程度有减少趋势，当刀具直径降到6 mm时，过切依然存在。这种现象表明，此时造成过切的关键原因并非刀具直径大小。

1.3 右刀补仿真加工

采用如图2(b)所示的右刀补，用数控程序O0042在斯沃仿真软件FANUC 0iM数控系统进行仿真加工(采用直径10 mm的端铣刀)，仿真效果如图5(a)所示。

在建立的ABAQUS有限元模型中，对于上面板和冲击头之间的接触引入通用接触，接触约束采用罚函数运算法则。上面板的网格要确保划分的足够精细，这样冲击头在与其接触的时候不至于发生穿透现象。另外，冲击部位的波纹夹芯层的网格也需要划分的特别精确，从而可以捕捉到波纹夹芯在冲击过程中发生的屈曲和压溃。

图3 左刀补斯沃仿真加工

图4 不同直径刀具左刀补仿真加工对照

具体代码如下：

O0042;

N01 G54 G90 G17 G40;

N02 M03 S800;

N03 G00 X0 Y-20;

N04 Z5;

N06 G42 X10 D01 F150;

N07 G02 X0 Y-30 R10;

N08 X-30 Y0 R30;

N09 X0 Y0 R15;

N10 X30 Y0 R15;

N11 X0 Y-30 R30;

N12 X-10 Y-20 R10;

N13 G40 G01 X0;

N14 G00 Z100;

N15 M05;

N16 M30;

采用右刀补的走刀方式，此时的仿真结果显示在尖角过渡的地方没有发生过切。在满足理论依据的前提下，适当增大刀具直径，对应的仿真结果如图6所示。

从图6可以看出，右刀补加工模式下，采用不同直径刀具仿真加工时，在尖角过渡处，均没有发生过切，符合加工要求。

2 型腔尖角过切分析

从上述左刀补和右刀补的仿真加工对比可知：在型腔尖角圆弧过渡处，若执行左刀补，则发生过切；若执行右刀补，则无过切出现，符合加工要求；在刀具直径符合加工要求的范围内，上述结果与刀具直径无关。

2.1 刀路测量分析

针对上述情形，打开斯沃仿真软件中的刀路测量，如图7所示。从图7可知，两种走刀方式在完成第一段R15的圆弧时，均与理论路线存在较大差异，虽然只执行N10一个程序段，但是对应偏移路线均为两段圆弧，这是执行了刀具半径补偿的结果。

图5 右刀补斯沃仿真加工图

图7(a)属于逆时针曲线相交过渡的左补偿类型，两段R15与中间小圆弧属于凹角衔接，存在明显过切。图7(b)属于顺时针曲线相交过渡的右补偿类型，两段R15与中间小圆弧属于光滑过渡，仿真加工符合要求。

两者均属于要增加过渡圆弧段作为补偿的情况，过渡圆弧段的起点是第一段R15偏置后曲线的终端，第二段R15偏置后曲线的起始点即为过渡圆弧段的终点。由于增加了过渡圆弧段的原因，在过渡地方易发生过切问题。为了解决此类过切问题，必须从这段新增的过渡圆弧段入手[4]。

图6 不同直径刀具右刀补仿真加工对照

图7 走刀路线图

2.2 刀具半径补偿矢量分析

在本例中，产生尖角过切的原因是由于两段圆弧过渡处新增了小圆弧导致，解决这类过切问题可采用刀具半径补偿矢量分析法[5]。

解决问题的核心在于计算偏移轨迹间的矢量方向和夹角，结合平面解析几何来进行计算。圆弧AB执行刀具半径补偿偏置为A′B′和B′C′，设A′B′和B′C′间的矢量夹角为α，利用矢量分析法可得两圆弧间的矢量乘积为：

A′B′·B′C′=|A′B′|·|B′C′|cosα

如图8(a)所示，此时α=π，运算结果小于零。当矢量乘积小于零时，刀具偏移方向造成过切。如图8(b)所示，此时α=0，运算结果大于零。当矢量乘积大于零时，刀具偏移方向不造成过切，仿真结果符合要求。

图8 矢量分析

3 结论

刀具半径补偿功能的应用给数控编程带来了极大的便利性，灵活应用刀具半径补偿功能在很大程度上实现了数控铣削粗加工到精加工的自由切换。但是，刀补建立、执行和撤销中存在的各类问题会导致过切的出现，因此如何正确解决这些问题，避免过切的出现是十分重要的。在型腔尖角过渡处产生的过切是型腔尖角加工中常见的现象，采用矢量分析法研究此类问题，通过平面解析几何的方向矢量算法，根据偏置曲线获得补偿圆弧的相关参数，得出刀具半径偏移矢量乘积值，可以有效地避免圆弧尖角过渡处出现的过切问题。该方法可以提高型腔零件“拐急弯”的加工精度和加工效率，是目前值得推广的可靠性高的方法之一。