扭转梁式光纤光栅加速度传感器分析与设计

周海阳 赵振刚 于 虹 姚 敏

（1.昆明理工大学信息工程与自动化学院；2.云南电网有限责任公司电力科学研究院）

在交通系统、建筑形变、电网输电及航天器状态监测等领域［1～4］，为了避免微小损伤长时间累积后造成实际危害，必须重点对工程的健康程度持续监测，尽早处理潜在问题，防止发生事故。 加速度信号测量是工程中常用的一种技术手段。 加速度传感器通过接收振动参数，不仅能直观地反映出物体的振动状态，还可以提取出位移、速度等其他振动特征量，用于健康监测或是故障诊断［5］。 光纤光栅加速度传感器由于质量轻、体积小、抗电磁干扰能力强且安全性能高而得到广泛研究和应用［6］。

目前，国内外研究者根据光纤光栅加速度传感器的原理设计了不同形式的扭转梁式结构。 王宏亮等研制的光纤布拉格光栅振动传感器采用了对称式的双等强度悬臂梁， 能够得到可靠的振动信号， 谐振频率为80.74Hz， 加速度灵敏度约为20.85pm/g［7］。 美国伊利诺伊大学的Talebinejad I等研究了一种基于等强度梁结构的FBG加速度传感器，谐振频率为150Hz，而灵敏度只有12.95pm/g［8］。在此基础上，Basumallick N等经过进一步研究，通过调整光纤传感器轴到悬臂中轴的距离， 使加速度传感器的灵敏度比文献［7］的设计增大了约两倍，提升到了45.90pm/g，而谐振频率只有十几赫兹［9］。 在光纤光栅加速度传感器的设计中，传统梁式结构普遍存在传感器灵敏度值提高会降低谐振频率、谐振频率提高会降低灵敏度值这一现象。

笔者提出了一种基于扭转梁式结构的光纤光栅加速度传感器。 首先理论分析了扭转梁结构的加速度信号检测原理，接着根据仿真结果再对结构参数进行调整提高其性能，最终能够实现在适当增大加速度传感器灵敏度值的同时不降低谐振频率范围，可检测高频信号。

1 扭转梁光纤光栅加速度传感器

1.1 光纤光栅传感理论

根据光纤光栅的耦合模理论［10］，光纤光栅由于波导与光波相互作用，使光纤中传输的光波从原来限定在纤芯中前向传输的模式耦合，变为限定在包层或纤芯中前向或后向传输的模式，从而得到特定的透射和反射光谱特性。 宽带光若满足布拉格条件，光纤光栅会将它反射回来，不满足条件的光则全部投射出光栅［11］。

光栅的布拉格波长λB可由下式确定：

式中 neff——纤芯有效折射率；

Λ——光栅周期。

由式（1）可知，纤芯有效折射率neff和光栅周期Λ是影响光纤光栅反射波长的两个因素。Λ的改变可以通过外界应力产生的压缩或拉伸作用实现。 在变化的应力作用下，布拉格波长随之变化，可用下式进行描述［12］：

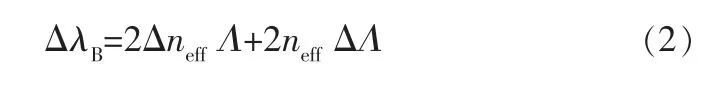
式中 ΔλB——光栅的布拉格波长变化量；

Δneff——纤芯有效折射率改变量；

ΔΛ——光栅周期改变量。

当应变施加在光纤光栅上时，光纤光栅的中心波长随应变大小不同发生相应变化。 将信号解调后，可获取中心波长变化量，经过运算后得到加速度信号。

1.2 传感器结构及原理

扭转梁式结构的光纤光栅加速度传感器主要组成部分有：扭转圆盘、扭转梁、质量块，传感器结构如图1所示。 主体是有一定厚度的扭转圆盘，圆盘上紧贴质量块，在扭转圆盘的外围贴有一根处于绷紧状态的光纤光栅。

图1 扭转梁式光纤光栅加速度传感器传感模型

当有外力施加于传感器上时，在扭转圆盘上质量块的带动下， 扭转梁产生微小的扭转形变量， 而与之相连的扭转圆盘能将这一微小量放大，扭转圆盘外围的光栅受到的拉力大小随扭转量变化而改变。

截面扭矩T计算公式如下：

式中 a——质量块转动角加速度；

A——截面面积；

l′——惯性力臂；

m——质量块质量；

TP——截面扭矩；

ρ——质量块距圆心的距离。

截面扭矩等于惯性力矩［13］，即：

式中 G——切变模量；

x——圆盘两侧距离；

γP——切应变；

φ——扭转角度。

将式（4）代入式（3）中得截面扭矩为：

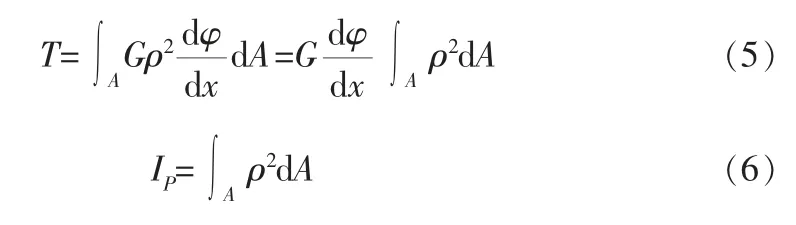
式中 IP——横截面极惯性矩。

因此，截面扭矩T可简化成：

设扭转梁长度为l，扭转圆盘半径为R，则扭转角度φ为：

光纤光栅所受应变ε为：

式中 l光——光纤光栅的栅区长度。

谐振频率f为：

式中 J ——转动惯量。

将质量块等效视为扇形体，质量块、扭转梁、扭转圆盘的转动惯量分别为J1、J2、J3，即：

式中 h1——质量块厚度；

h2——扭转圆盘厚度；

r——扭转梁半径；

r1——质量块到扭转梁中心内圈半径；

r2——质量块到扭转梁中心外圈半径。

总转动惯量为J=J1+J2+J3。

2 扭转梁光纤光栅加速度传感器有限元分析

2.1 初始结构参数仿真

利用ANSYS软件对扭转梁式结构的光纤光栅加速度传感器进行有限元仿真分析，以获得不同结构下的物理特性。 仿真流程如图2所示。

图2 仿真流程

影响传感器性能的参数主要有：扭转梁的直径和长度，扭转圆盘的直径和厚度，质量块的内径、外径、角度及高度等。 对传感器进行模态有限元分析和静态有限元分析，初始结构参数如下：

扭转梁

半径r 1.5mm

长度l 21mm

扭转圆盘

半径R 12.5mm

厚度h23mm

质量块

内径r17.75mm

外径r212.50mm

角度φ 60°

厚度h16mm

对于该传感器的结构，将“扭转梁两端面位移为0”设置为边界条件。 在进行模态有限元仿真分析时不需要施加负载。 向传感器施加加速度信号后，分析三阶振动结果。 一阶振动方向指扭转梁做沿轴向旋转的运动；二阶振动方向指扭转圆盘整体在竖直方向产生的运动；三阶振动方向指扭转圆盘整体在水平方向产生的运动。 图3为对应三阶分析的结果。

初始结构方案设置下每一阶振动方向对应的振动频率如下：

一阶 1 032.2Hz

二阶 2 848.4Hz

三阶 3 759.2Hz

对初始方案进行静态有限元仿真分析时，需要在竖直方向先施加一个大小为1g（g=9.8m/s2）的加速度信号，出现的最大位移为9.804×10-5mm，仿真结果如图4所示。 图中红色区域位置表示出现最大位移，深蓝色区域位置表示出现最小位移。

通过模态有限元分析可以发现，当施加加速度信号在传感器上时，传感器的扭转梁在二阶和三阶方向上受到的影响明显减小。 此外，通过对比发现高阶模态谐振频率是一阶模态谐振频率的两倍以上，不会影响低阶振动信号的产生。

通过静态有限元分析可以看出，对传感器结构施加加速度大小为1g的作用后，质量块位置和扭转圆盘外围都产生了显著的位移变化，最大位移9.804×10-5mm。

2.2 传感器的增敏设计

由于实际工程可行性的要求，传感器灵敏度越高越有利于实际运用。 笔者提出如下方案：

a. 方案一，保持其他参数不变，将扭转梁的半径减小到1mm，使之变得对加速度做出更敏感的反应，得到的扭应变量相比原来更大；

b. 方案二，保持其他参数不变，把扭转圆盘的半径增大到15mm， 使紧贴在扭转圆盘侧面上的光纤光栅缠绕半径更大，增大了扭转圆盘上的扭应变，外力作用更加明显。

两种增敏方案下所设置的参数见表1。

表1 两种增敏方案下传感器的结构参数

对增敏方案一的传感器进行模态有限元仿真分析和静态有限元仿真，分析过程如图5所示，各阶振动频率如下：

一阶 689.7Hz

二阶 2 130.6Hz

三阶 2 733.2Hz

图5 增敏方案一传感器结构有限元分析结果

当施加加速度信号在传感器上时，传感器的扭转梁在二阶和三阶方向上受到的影响明显减小。 质量块和扭转圆盘外围部分都产生了显著的位移变化，最大位移为2.137×10-4mm。

对增敏方案二的传感器进行模态有限元仿真分析和静态有限元仿真，分析过程如图6所示，各阶振动频率如下：

一阶 1 022.7Hz

二阶 2 491.2Hz

三阶 3 201.1Hz

图6 增敏方案二传感器结构有限元分析结果

该结构的扭转梁光纤光栅加速度传感器在1g加速度作用下，质量块和扭转圆盘外围区域均产生最大位移，位移量为1.119×10-4mm。

在增敏方案一中通过改变扭转梁半径，传感器的加速度值有了较大的提高，但传感器的谐振频率却大幅度减小，频响范围变窄。

增敏方案二对比初始结构1 032.2Hz的谐振频率几乎没有减小，而且增敏方案二的静态最大位移为1.119×10-4mm，较初始结构的9.804×10-5mm有了提升，提高了传感器的灵敏度。

3种方案下的有限元分析结果对比见表2。 可以看出，按照增敏方案二的优化，增大扭转圆盘半径，使紧贴在扭转圆盘侧面的光纤光栅缠绕半径更大，提高了传感器灵敏度，但同时保证谐振频率不改变，解决了传统梁式结构加速度传感器设计中存在的加速度灵敏度提高会导致谐振频率降低这一问题。

表2 传感器的增敏结果对比

2.3 灵敏度计算

根据静态有限元分析结果，利用最大位移量来计算传感器的加速度灵敏度。

由于光纤光栅沿传感器被紧密贴合在扭转圆盘外围，扭转圆盘外围受到加速度信号影响发生的位移可以转化为光栅在圆盘切线方向受到的拉力产生的位移。 可计算出光纤光栅所受的应变ε为：

式中 Δx——光栅栅区因受拉变形产生的位移。

传感器的加速度灵敏度s为［14］：

将初始方案和两种增敏方案设置的参数代入到传感器数学模型中，分别计算求出传感器谐振频率和灵敏度的理论值、仿真值（表3）。

表3 传感器理论参数与仿真参数对比

通过对比发现：增敏方案一相对初始结构方案来说，只是减小了扭转梁的半径，使扭转梁变得对加速度信号更敏感， 但从数据中也能发现，无论是仿真值还是理论值，谐振频率均出现大幅度减小，使传感器的频率范围相比原来更窄。 增敏方案二相对初始方案来说，保持扭转圆盘质量不改变，增大扭转圆盘的半径，这样使得被绷紧贴合在圆盘侧面的光纤光栅半径变大，从而使扭转圆盘旋转时，对光纤光栅带来的拉力变化更显著。 增敏方案二谐振频率的理论值和仿真值与初始方案的相比，虽然有减小但是幅度不大，结构上的改变获得了灵敏度的提升，效果最优。

3 传感器的研制及性能参数

为了验证初始结构和增敏方案的效果，对传感器进行加工制作。 对应初始结构方案、增敏方案一、增敏方案二的结构，分别制作了3支加速度传感器，标注为A、B、C，实物如图7所示。

图7 传感器实物

将3支传感器进行测试，结果见表4。 实际测量的参数与计算值、仿真值存在一定误差，传感器的制作过程中已尽可能保证制作工艺和环境条件一致，但仍然存在一定误差。

表4 传感器性能参数汇总表

通过对前文提到的3种设计方案进行实物制作和测试后，发现传感器B相对传感器A虽然在灵敏度上有了巨大提升，却以牺牲谐振频率作为代价，同时与另外两支传感器相比，实测值与理论值、仿真值相差较大。 相比较而言，传感器C与传感器A的谐振频率相差不大， 但灵敏度却有很大提高。 此外，通过对比也发现，传感器C的线性度、重复性误差、迟滞性误差均有所增大，在这些性能指标上不如传感器A、B。

4 结束语

根据扭转梁式结构参数，提出了一种光纤光栅加速度传感器，对传感器进行了有限元仿真分析、加工制作、性能参数的分析。 研究结果表明，依据增敏方案二所设计的传感器C与依据初始结构方案所设计的传感器A相比，谐振频率保持在1 180Hz左右的同时， 灵敏度有一定提升， 达到6.290pm/g。 与增敏前的结构相比，实测灵敏度相对传感器A提高了22.97%。 通过改进传感器的结构，能保证在不降低加速度传感器谐振频率的同时提高灵敏度，具有更高的测试带宽，可实现对高频信号的检测。