帝国竞争算法优化板球系统PID参数控制研究
2020-06-22黄文杰向凤红毛剑琳
黄文杰 向凤红 毛剑琳
(昆明理工大学信息工程与自动化学院)
板球系统具有非线性系统的不确定性,是一类强耦合、欠驱动动力学系统的代表[1]。在这个系统中, 大量的优化方案被应用于小球的定点、轨迹跟踪等运动。 李爱莲和吴何琛在图像处理上的优化方案也被成功应用于其中[2,3]。 PID控制作为一种经典且有效的方法不仅在试验研究中广泛应用, 工业生产中的PID控制也很常见。 然而,Roy P等学者发现, 由于板球系统对控制精度的要求较高,且实际控制中具有不确定性,PID控制始终无法在板球系统的控制中保持较好的物理非线性完整度[4,5]。 20世纪70年代以后,智能算法大量问世,遗传算法(GA)[6]、粒子群算法(PSO)[7]及蚁群算法(ACO)[8]等运算能力较强的控制算法相继与PID控制法相结合, 大幅度提高了其寻优能力。但是,GA算法在处理较高维数的参数时,易早熟并陷入局部收敛;PSO算法参数较多,在处理关联性较大的参数能力上显出不足;ACO算法则有收敛速度慢导致控制时间长的问题[9~11]。 因此,这些算法应用于板球系统这一类欠驱动、强耦合的非线性控制系统时,其效果并不理想。
笔者提出了一种新的可应用于板球系统的基于帝国竞争算法(ICA)的PID控制方法。 选取GBP2001型板球系统作为研究对象, 主要对小球进行定点控制。将试验数据导入Matlab软件,与传统的PID算法和GA-PID算法进行对比, 看出笔者提出的ICA-PID算法在板球定点控制过程中取得了较好的效果。
1 GBP2001型板球系统建模
以固高GBP2001型板球系统(图1)作为试验平台, 以平板的支撑点作为原点建立坐标系,分别在x、y两个方向对板球系统完成解耦, 得出x方向和y方向的二维分解示意图如图2所示。

图1 GBP2001型板球系统
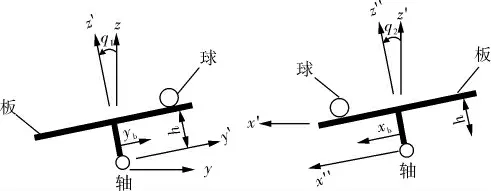
图2 板球系统二维分解示意图
板球系统包括小球位置坐标(x,y)、平板转动角度(q1,q2)等变量,由于板球系统是复杂的非线性系统, 难以获取其精确的数学模型, 对建模过程中在不影响系统特性的情况下作以下假设:
a. 小球在平板上无滑动和绕小球垂直中心轴旋转的运动;
b. 忽略小球与平板的角度以及平板面积的影响;
c. 小球在平板上时始终与之保持相接触的状态;
d. 建模过程中,将小球和平板之间所有摩擦忽略不计。
建立系统的数学模型对于控制器的设计非常重要,由于板球系统属于一类复杂的非线性系统,为此笔者从能量的角度建立以拉格朗日法为基础的数学模型。 板球系统中的各个参数见表1。

表1 板球系统参数表
以平板的几何中心点为原点建立坐标系,由于在忽略损耗的情况下能量保持守恒,设小球动能为Tb,平板的动能为Tp,则总动能T=Tb+Tp。 对小球和平板分别列出能量方程:

同理, 板球系统总势能V包括小球势能Vb与平板势能Vp,即V=Vb+Vp。 由于在能量分析中取平板为零势能点,故Vp=0。 小球势能如下:

以拉格朗日法建立函数如下:

在实际操作中, 电机转动位置不受力矩影响,故将式(3)、(4)线性化后可得方程:

2 板球系统控制器设计
2.1 PID控制器
PID控制器已经广泛应用在工业生产的过程控制中,它具有安装简单、鲁棒性强等特点。 PID控制原理如图3所示。
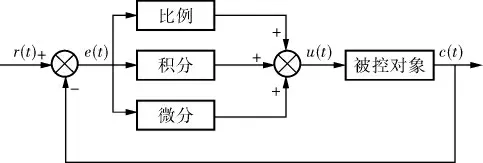
图3 PID控制原理
控制算法为:

其中,Kp为比例系数,Ki为积分系数,Kd为微分系数;r(t1)、r(t2)、r(t3)是系统的3个输入量,用控制误差e(t)来表示:

2.2 板球系统的GA-PID控制器
遗传算法是借鉴了进化论和遗传学的一种基于自然选择和群体遗传机理的搜索算法[12]。 其算法机理主要包括选择、 交叉及变异等操作,经过优胜劣汰的过程,种群向最优解不断进化。 因此, 遗传算法就是群体不断淘汰和进化的过程,交叉概率Pc和变异概率Pm的值共同决定了算法的收敛性。 板球系统中应用遗传算法优化PID参数主要有以下几个步骤:
a. 随机产生N个二进制字符串, 取初始种群数量为100、迭代次数为20、交叉概率Pc为0.5、变异概率Pm为0.05;
b. 计算各个体的适应度值以便参数寻优;
c. 应用遗传算法的复制、交叉和变异算子对群体进行操作;
d. 选择适应度高的个体,同时淘汰适应度低的个体;
e. 重复步骤c、d, 直至算法收敛或达到终止条件;
f. 最终的Kp、Ki、Kd值表示群体中适应度最好的字符串。
2.3 ICA的应用流程
2.3.1 初始化过程
在ICA中,初始解(country)由向量定义。 笔者研究的问题可以转化成大小为1×N的向量:

每个国家的成本值用函数f(country)来评估,类似于遗传算法中的适应度函数:

初始化帝国竞争算法,最初国家的数量定义为Npop, 选择Nimp作为实力最强的国家建立帝国,其余的Ncol(Ncol=Npop-Nimp)作为帝国殖民地。因此,帝国由帝国主体和一系列殖民地组成。 在最初的帝国集团里, 殖民地数量必须与其能量大小有关, 能量大的帝国拥有的殖民地数量也就越多,反之,则越少。 各个殖民地在帝国主体间按照比例被分配,其分配方法如下:
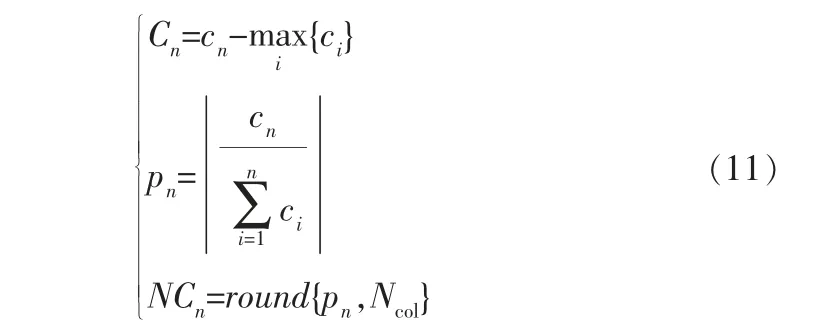
其中cn是第n个帝国的初始成本,减掉帝国中成本最大值后即为相对成本值Cn;pn为第n个帝国初始化分配后的势力大小;NCn是第n个帝国分配到的殖民地数量。 殖民地在最初分配时依据随机分配的原则,但势力强大的帝国会拥有更多的初始殖民地,势力弱小的帝国会被分配到更少的殖民地数量。
2.3.2 同化过程
在形成了最初的帝国之后,每个帝国的殖民地都开始通过向其相关的方向发展来提高自己的实力。 这个过程的目的是为了使殖民地问题解的结构与帝国所代表解的结构更相似,所以被称为同化过程(图4)。
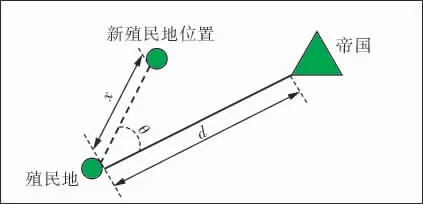
图4 同化过程示意图
如图4所示, 殖民地向帝国方向移动x个单位,其中x是一个随机变量,服从均匀分布,可表示为:
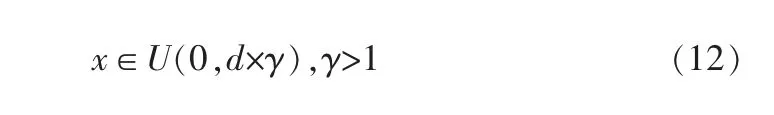
其中,未同化之前帝国与殖民地之间的距离为d;γ是大于1的实数,保证殖民地能从不同的方向靠近帝国。 最初的运动方向本质上不是殖民地和帝国之间的矢量,为了模拟这个事实,将偏差参数θ并入同化过程中有助于提高搜索能力。 θ的恰当选择对于帝国的集群化和多元化有很大影响,通常θ取π/4能够很好地达到全局收敛效果[13]。
2.3.3 革命过程
与遗传算法中的突变过程相似,ICA允许国家的社会政治特征突然出现变化,这个过程被称为革命。 革命过程的出现能够防止同化后算法在早期迭代中就收敛到局部最优解。
2.3.4 更新及合并过程
在同化和革命过程之后,一个殖民地可能达到一个比它的成本还低的位置, 如同人类社会中,大多数帝国主义国家会选择一个具有生存优势的位置确定都城,这种情况下就需要互换殖民地与帝国的地位:当前帝国变为殖民地,殖民地取代当前帝国。 图5为帝国更新示意图。

图5 帝国更新示意图
2.3.5 竞争过程
一个帝国集团经过更新、合并等过程之后会具备一定的整体实力,这种整体实力是指主体帝国与所拥有的殖民地的能量的总和。 总成本TCn用帝国初始成本和包含的殖民地成本相加计算:

其中,wi为帝国集团的殖民地的代价函数值;ξ是介于0~1之间的非负数,ξ越小,帝国的总成本就越接近帝国国家的成本,反之越小。
帝国竞争算法最重要的步骤之一是构建帝国集团之间的竞争过程。 在这个机制中,最弱国中最弱的殖民地有极大的可能会被较强的帝国抢夺,各个帝国集团在竞争中生存。 最终导致的结果就是强的帝国越来越强, 弱的帝国越来越弱。 为了开始这一过程,首先要对每个帝国的总成本进行标准化,并计算占有概率Pn:
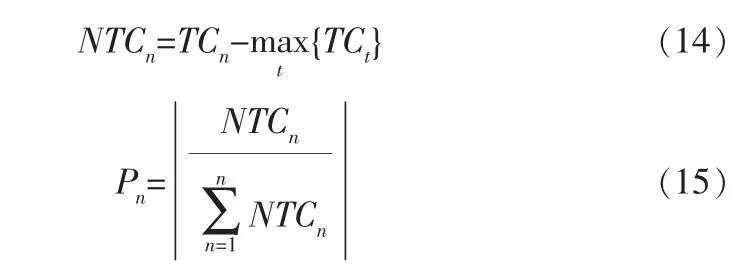
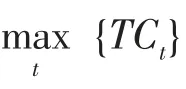

R为与Q大小相同, 参数介于0~1之间的通过均匀分布随机数组成的向量。由向量Q减去R来计算向量D,D值最大的帝国即可占有自由殖民地。这种帝国获取殖民地的方式只需极小的计算量,极大地提高了算法的计算效率。 与遗传算法在交叉操作时选择母类的轮盘赌过程相似,但该算法因为不需要计算累积分布函数,能够以更少的迭代次数寻找到全局最优点, 大幅提高了寻优速度,从而减少了板球系统的控制时间。
2.3.6 帝国崩溃与融合过程
在帝国竞争中, 影响力小的帝国会被强大的帝国掠夺从而逐渐失去他们的殖民地, 这导致弱小的帝国随着时间的推移而崩溃, 最后所有的殖民地都被最强大的帝国占领。 当所有帝国中最强大的一个帝国保存下时算法终止,设置一定的迭代次数, 可选取算法停止时势利最强的帝国作为输出的最优解。 将上述算法应用于板球系统PID控制器的整定过程中,并设置跟踪单位阶跃响应曲线的对比试验验证算法的优越性。
3 板球系统控制试验
3.1 板球系统仿真试验
采用传统PID、GA-PID和笔者提出的ICA-PID这3种控制方法分别进行试验, 其中GA-PID控制算法根据文献[14]的策略,设置种群数量为100、变异概率为0.05、交叉概率为0.5;ICA-PID算法中设总国家数为200、帝国数为8。 3种算法优化同一个数学模型:

PID参数寻优后, 单位阶跃响应如图6所示,参数对比见表2。
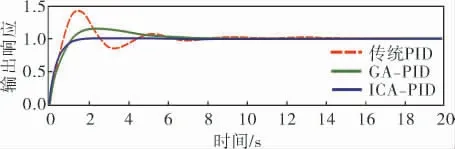
图6 单位阶跃响应对比曲线
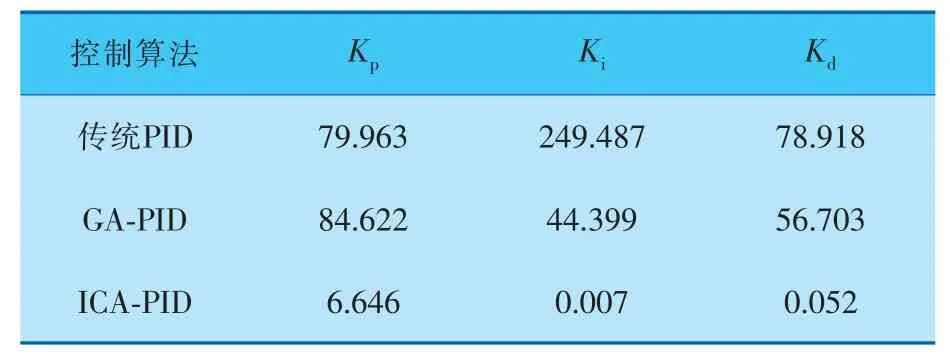
表2 参数对比
综上可以得出,采用ICA整定的PID阶跃响应比传统PID和GA-PID对控制器的寻优效果好,在板球系统控制试验中具有调节时间短、收敛速度快和稳态误差小的优点。
3.2 板球系统轨迹跟踪试验
为验证ICA-PID控制算法的实际可行性,另外设置了基于固高GBP2001型板球系统作为试验平台的定点轨迹跟踪试验, 开始控制时初始PID参数值设置为Kp=20、Ki=1、Kd=120。 采用上述3种控制算法分别完成小球运动并稳定停止在原点的控制试验,记录小球稳定后的试验数据。
在忽略小球初始位置、光照强度等干扰因素的影响下进行试验,将最终数据导入到Matlab,以仿真曲线的形式反映小球在x、y两个方向上的坐标误差变化和运动轨迹(图7),具体数据见表3。

图7 小球坐标误差变化和运动轨迹

表3 小球轨迹跟踪误差对比
在定点控制试验中,ICA-PID控制算法的小球轨迹较为简洁, 稳定后的误差值相对较小,基本满足了控制精度的需求。 根据表3,在控制时间方面, 相比于传统PID控制算法,ICA-PID控制算法能够大幅度缩短控制时间,减小控制误差并且优化了PID控制整定参数不良的缺点, 其优化效果相比GA-PID算法在稳定性和缩小超调量方面也具有优势。
4 结束语
主要研究了GPB2001非线性板球控制系统,提出了ICA-PID算法整定PID控制参数,以实现板球系统控制的优化。 单位阶跃响应和小球定点控制仿真试验,证明了ICA-PID算法在整定PID参数方面具有较强的参数寻优能力,在板球系统中能够成功应用并且得到不错的控制效果。
