多个参数变化对真空严密性综合影响的计算

2020-06-22旷仲和

热力透平 2020年2期

旷仲和

(华能国际电力股份有限公司广东分公司海门电厂，汕头 515000)

在设计参数、正常运行方式工况下，汽轮机真空严密性随漏气量的变化而变化。由于漏气量测量难度大，而真空严密性试验相对容易做，故实际工程中通常把真空严密性当作漏气量程度的表征方式以及考核验收指标。

但是，在汽轮发电机组的有关参数偏离设计值时，这些参数的变化会引起真空严密性的变化。已经有文献证明某一种参数的变化对真空严密性有影响，而且还能根据某一参数变化的大小，来定量计算其对真空严密性影响的大小。然而，当各个相关参数同时变化时，它们对真空严密性的影响如何计算，这在工程上是一个非常实际的问题。

本文根据文献[1-4]研究的成果，将采用高等数学相关知识，推导相关解析计算法以及对真空严密性的修正计算法。该方法能定量计算各类相关参数的同时变化对真空严密性的影响大小，并把真空严密性修正到设计或规定状态。利用此方法能够帮助分析真空严密性降低的原因，对于避免各种参数同时变化对真空严密性试验值的误判断具有实际意义。

1 分析依据

1.1 常用符号说明

本文涉及大量参数与公式的计算，相关常用符号集中说明如下(除在文中另有说明)：

N—汽轮机发电功率，或发电负荷，MW

K—冷却水管总的传热系数，kW/(m2·K)

Ko—冷却水基本传热系数， kW/(m2·K)

βc—凝汽器冷却水管清洁系数

βt—冷却水入口温度修正系数

βm—冷却水管材质与壁厚修正系数

Qk—凝汽器吸收的当量热量，kJ/s

Dk—汽轮机排汽当量流量，kg/s

ik—汽轮机当量排汽焓，kJ/kg

Sk—汽轮机当量排汽熵，kJ/(kg·K)

a、b、c—分别为按最小二乘法拟合的二次三项式的待定系数

tw1—凝汽器冷却水进口温度，℃

tw2—凝汽器冷却水出口温度，℃

cp—冷却水定压比热容，kJ/(kg·K)

Gw—冷却水流量，kg/s

A—凝汽器冷却水管外表面积，m2

Δtm—冷却水对数平均温差，℃

Δh—当量排汽热焓与当量凝结水热焓的焓差，kJ/kg

hs—当量排汽热焓，当变工况时，假设汽轮机为绝热膨胀，其由已知背压与当量排汽熵确定，kJ/kg

hc—当量凝结水焓，hc=4.187(tk-0.5)，0.5为设计凝结水过冷却度，kJ/kg

tk—汽轮机排汽温度，℃

Ga—漏入真空系统的干空气量，kg/h

V—系统真空容积，m3

pk—汽轮机背压，kPa

Y—参数变化引起的对真空严密性的变化率

本文不讨论凝结水溶解氧变化、大气压对真空严密性的影响，故其相关参数代号不列入。

1.2 综合参数对真空严密性的影响计算

根据文献[1-4]，真空严密性(用真空下降速度来表征)与相关参数的关系如下：

(1)

根据文献[5]求全微分的方法,对式(1)求全偏微分，得到：

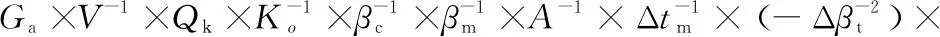
把式(2)改为增量形式，并除以式(1)，得到：

式(3)表明：多个参数同时偏离设计值变化所引起真空严密性的变化率，等于各个参数分别偏离设计值变化引起的真空严密性变化率的代数和。

1.3 单个参数偏离设计值的计算

式(1)以及式(3)中的单个参数偏离设计值对真空严密性影响与对真空严密性变化率影响的计算，都需要满足以下计算公式：

Qk=Gw×cp×(tw2-tw1)

(4)

Qk=Dk×ik-4.187×Dk×(tk-0.5)

(5)

Qk=K×A×Δtm或

Δtm=Qk/(K×A)

(6)

K=Ko×βc×βt×βm

(7)

Δtm= (tw2-tw1)/ln [ (tk-tw1)

/(tk-tw2)]

(8)

(9)

式(4)至式(9)中的各项参数根据文献[6-7]、文献[9]的方法确定。其中的cp根据已知的冷却水压力与温度确定，ik根据已知的汽轮机热力膨胀过程曲线的排汽压力与排汽熵确定，tk根据已知的或已经求得的排汽压力确定。其具体的计算参考文献[8]。

使任一个参数发生变化而影响相关参数的变化，就是变工况计算。进行这种变工况计算的方法一般采用试算法。其试算结果要使式(1)至式(9)同时满足。其具体计算方法参考文献[1-4]进行,本文不复述。

把按上述计算得到的各个参数的相对变化率代入到式(4)中，就得到各个参数同时变化对真空严密性影响的综合变化率。

1.4 修正系数的计算

多个参数变化时，其变工况真空严密性与设计值或规定值之间的关系为：

(10)

把式(10)变换为：

(11)

(12)

将式(12)中的Y定义为多个参数同时变化对真空严密性影响的变化率，即为：

(13)

将1+Y定义为多个参数同时变化对真空严密性影响的综合修正系数。

修正后的真空严密性为：

(14)

单个参数变化对真空严密性的影响是多个参数同时变化对真空严密性影响的特例。因此，式(13)至式(14)也适用于单个参数变化的情况。此时其表达式为：

(15)

1.5 参数修正曲线图的绘制、修正系数方程式的拟合

根据上述每个变工况参数计算得到的数据，可以绘制参数修正曲线图。该图横坐标为某单一参数，纵坐标为相应的真空严密性变化率。此图可以用于真空严密性试验单个参数变工况任一点的修正计算。

修正曲线需要人工查图取得数据，存在视觉误差，而且不便于计算机程序计算。此时可以按最小二乘法原理拟合为二次三项式。以冷却水温度变工况为例，其拟合的方程式为：

(16)

将已知的冷却水温度之值代入上式中，就能计算其相应的变化率。

其他参数修正方程式的拟合与计算跟上式相同，此处不再详述。

2 示例

2.1 原始数据资料及计算目的

某电厂一台容量为600 MW的凝汽式汽轮发电机组，在热耗率验收(THA)工况下的参数如下。

汽轮机本体侧：主蒸汽压力24.2 MPa，主蒸汽温度566 ℃；当量排汽流量293.564 kg/s，排汽焓2 322.26 kJ/kg，排汽熵7.632 2 kJ/(kg·K)，排汽压力4.83 kPa，排汽温度32.26 ℃。

凝汽器侧：凝汽器吸收热量642 988 kJ/s，冷却面积36 000 m2；过冷却度-0.5 ℃；冷却水管材料TA1，直径25 mm，厚度0.5 mm；进口冷却水流量69 300 t/h，压力0.2 MPa，温度21.9 ℃；质量体积4.183 m3/kg；清洁系数0.85，基本传热系数4 048 W/(m2·K)，温度修正系数1.007 2，冷却水管壁与材质修正系数0.952；总传热系数3 299.23 W/(m2·K)。

汽轮机-凝汽器系统：真空下降速度0.27 kPa/min；对应的漏气量72.38 kg/h；有效真空容积163.8 m3,大气压力为设计大气压0.101 MPa。

假设在参数变工况下，凝汽器面积、有效真空容积、凝汽器冷却管厚度不变,凝结水含氧量不变,各个相关真空系统稳定运行。汽轮机试验负荷为570 MW,冷却水温度为18 ℃，冷却水流量为18.3 t/s，清洁系数为0.835，真空下降速度为0.285 kPa/min。

根据上述参数以及条件，计算：(1)单个参数变工况下的真空严密性变化率；(2)单个参数变化与真空严密性变化率关系方程式的拟合；(3)各个参数同时变化对真空严密性的综合影响；(4) 各个参数综合修正后的真空严密性。

2.2 计算

2.2.1 各个参数的变工况下真空严密性变化率计算

文献[1-4]已经根据上述已知的设计参数，按照式(1)至式(15)分别计算了各个参数单独变化引起相关参数以及真空严密性相应变化。其数据如表1至表4所示。

表1 冷却水进口温度对真空下降速度影响及其修正的计算表

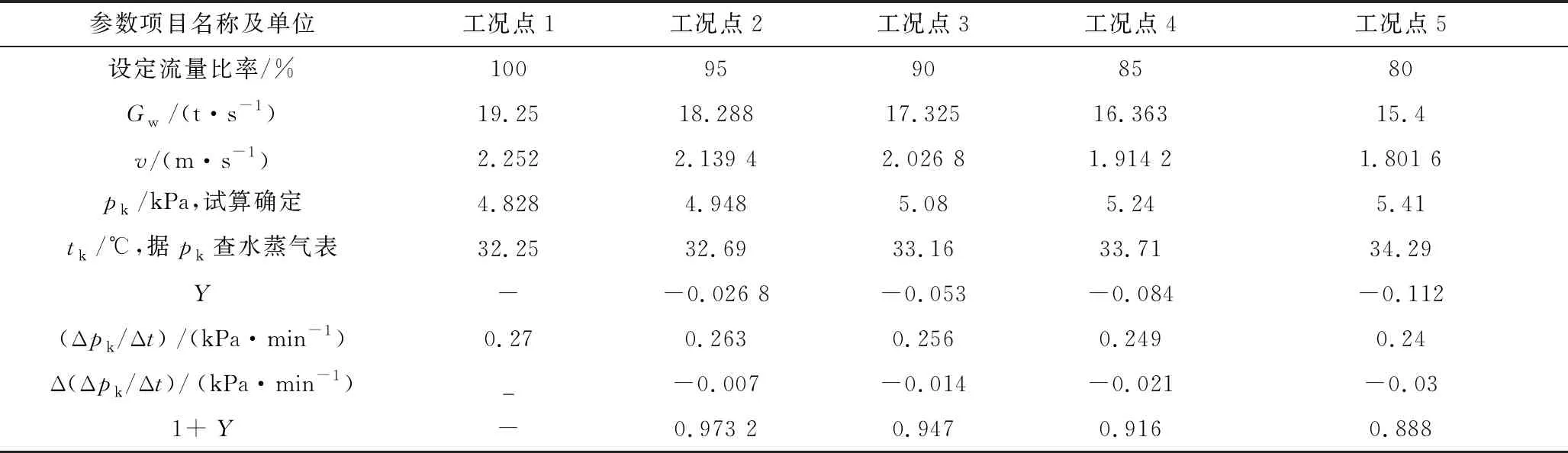
表2 某厂600 MW机组冷却水流量变化(100%～80%)对真空下降速度影响计算

表3 某厂600 MW汽轮发电机组清洁系数变化对真空下降速度影响计算

表4 某厂600 MW机组负荷变化对真空下降速度影响计算

2.2.2 参数与真空严密性变化率之间关系方程式的拟合

根据上述计算结果，以式(16)形式的数学二乘法，拟合相关公式如下。

冷却水温度与真空严密性变化率的关系式：

Y=0.484 81-0.034 33tw1+0.005 537tw12

(17)

冷却水流量与真空严密性变化率的关系式：

Y=-0.726 2+0.048 37Gw-0.000 552 8Gw2(18)

清洁系数与真空严密性变化率的关系式：

Y=-1.481 4+2.292 2βc-0.646 2βc2

(19)

汽轮机负荷与真空严密性变化率的关系式：

Y=-1.614 6-0.003 739N+

0.000 001 746N2

(20)

2.2.3 各个参数对真空严密性的综合影响

按照式(15)，单个参数Y值的计算如表5所示。

表5 变工况参数计算结果

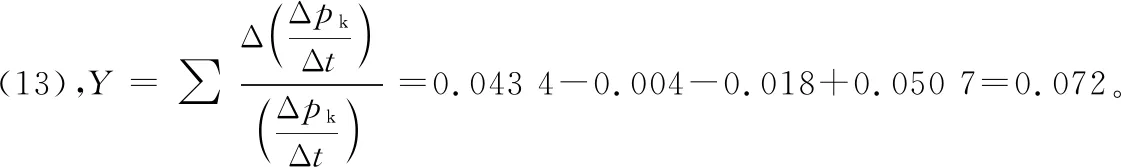
2.2.4 修正后的真空严密性

2.3 计算结果分析

根据计算结果可知，各个参数与真空严密性变化率之间的关系曲线光滑且连续，拟合的方程式计算的数据与原数据相比误差很小。由此，可以认为此方法具有足够的准确性。

根据示例说明，多个参数同时偏离设计值对试验的真空严密性试验值有综合影响。如果不进行修正，则容易造成对真空严密性的误判断。此例中试验值为0.285 kPa/min，参数修正后为0.266 kPa/min，原来试验是不合格的，但修正后却是合格的。如果将合格值误判断为不合格，会造成不必要的检修；如果将不合格值误判断为合格，又会导致机组的不经济不可靠运行。由此说明对真空严密性试验值进行综合参数修正，是必要的。