猜测、画图、想象：为发展儿童创造力添砖加瓦

沈亚

摘 要：数学课中培养学生的创造力，需要教师对教材进行深度挖掘，大胆设计，留给学生充足的思维想象空间。知识的内化需要学生富有个性化的理解和自我建构。学生猜想的提出并非凭空臆测，而是基于问题的分析及推测;画图操作有助于思维的具象与发散;想象能让创造的思维插上翅膀。

关键词：猜测;画图;想象;创造力

近日，在校本研修活动中，笔者有幸观摩了一节广州佛山举办的全国赛课一等奖的课例，周璟老师的“用数对确定位置”，给人留下较深的印象。其中环环紧扣的教学环节，新颖十足的情境设计，大气稳妥的现场把控令人赞赏，更让人惊叹的是对学生创造力的培养渗透在教学的各个环节。数学课上如何激发学生的创造力，一直是一线教师孜孜寻求的，儿童创造力的发展跟前沿科学家们长期酝酿顿悟后的发现是有区别的，他们的创造需要基于具体情境，经独立思考或合作交流迸发出“奇思妙想”。

一、有效观察，合理猜测

“猜想”指的是对现象或规律作出假定性推断和预测的思考，属于个体认知思考的表象形式之一。而要提升创造力的方法之一，就是要为你投身的事业增添趣味感。用数对确定位置大部分选取的情境是座位找人，即先给定具体的位置，让学生在自然状态下根据自身不同的表示方法来确定位置，而本课打破了这一常规思路，根据“蛙声”猜青蛙的位置，这一创意十足的数学情境为学生的观察提供了必要的猜测基础，通过鲜明的感知材料，多种感官的刺激、多角度的观察，从而引出合理的猜测。

[片断一]

师：小乌龟和小青蛙是最要好的朋友，有一天，小乌龟来找小青蛙玩。小青蛙故意躲在了一片荷叶的下面。它躲在哪儿呢？（如图1）

师：我们一起来帮小乌龟喊：“小青蛙，你在哪儿？”

小青蛙：哇、哇、哇、哇;哇、哇。

师：听懂了吗？小青蛙在用蛙语告诉我们它的位置。谁有想法了？

学生根据蛙声的特点，大胆猜测出了四种可能。

师：找到了4个位置，好像都有可能。看来，只知道4和2还不够哦。那小青蛙到底在哪里啊？没办法，我们把它请出来，好不好？

师：小青蛙你躲在哪里啊？（如图2）谁猜对了？这位同学，请你给我们再来翻译一下，4和2分别表示什么意思？

生：从左往右数的第4列，从下往上数的第2行。

师：原来第1个数字表示的是列，第2个数字表示的是行。

4和2确定的这个点就是小青蛙的准确位置。像这样的一对数，在我们数学上，把它叫作数对。

苏斯博士曾说：“想想左边，又想想右边，想想低处，再想想高处。啊，只要你尝试，你会有多少奇思妙想啊！”观察图，倾听声，分析可能，合理猜测小青蛙的藏身之所，妙趣横生的数学故事情境，让学生在观察时思考，在思考中观察。学生猜测的提出并非凭空臆测，而是基于问题的分析及推测。这样的观察，可激发学生多感官协同参与，让观察与思维紧密联系。很多类似的案例多从数学规定的角度灌输给学生，学生不管怎么推测都不及一个“规定”来的重要？而本课设计的亮点之一就是有学生猜对，再通过学生的理解，翻译蛙语的含义，这样能很好地将数学的核心知识与儿童猜测思维进行无缝对接。

二、由点到线，由线到图

托尼·赞布和巴利·赞布曾指出：一图胜过千言万语。由此可见，图像比文字更有感召力，更准确，更能激发学生多方面的联想力，所以更能提高学生的创造性思维和记忆。

[片断二]

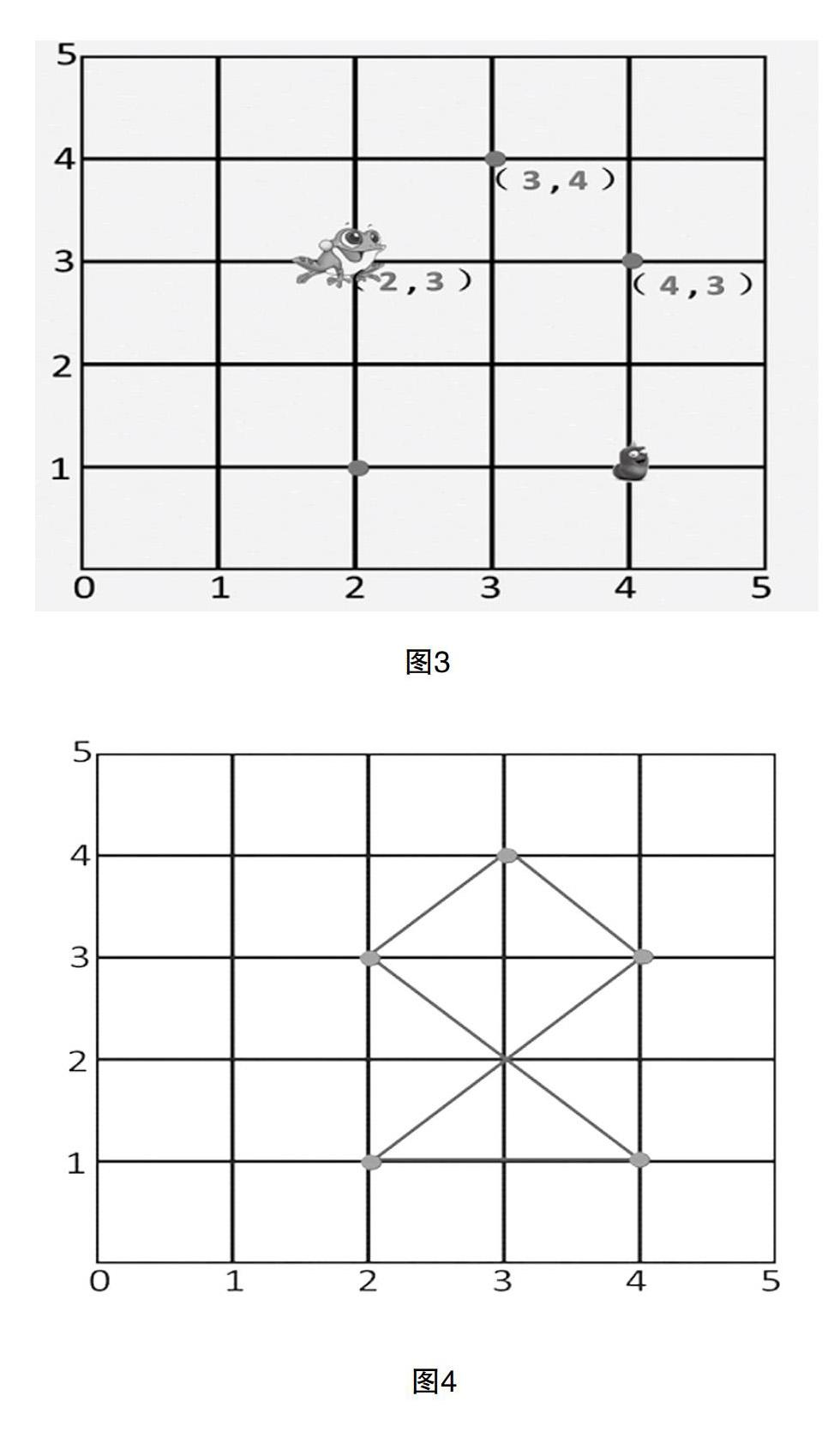
师：小青蛙除了会“呱呱呱”，它还是捉虫高手。请你将小虫的位置用数对告诉它。（如图3）

师：在你们的帮助下，小青蛙将所有的小虫子都给吃光啦。观察一下，刚才小青蛙抓虫的路径好像，好像什么呀？（如图4）

生：像一条鱼。

师：看来小青蛙不仅抓虫厉害，它还有画画的天赋。为了感谢你们，小青蛙特意准备了一幅画送给你们。画呢？难道这就是画吗？这不就是数对吗？有谁明白小青蛙的意思吗？

生：小青蛙就是說让我们沿着数对画下去，画出来的画就是送给我们的画。

师追问：每个数对可以画出什么？

生：一个点。

师：翻到练习纸1，请你将数对表示的点画出来，（待画完）这是什么呀？（如图5）看上去，好像什么都不像，对不对？

师：再看看小青蛙怎么说，再将数对的两个数交换位置，接着画，嘿嘿！如果A的两个数交换位置，那么还是（2，2）那B的两个数交换位置呢？（4，2）还是原来那个点吗？那其他的点交换两个数的位置，新的点在哪儿呢？请你接着画。

师：是这些吗？把它连起来，是什么呀？（如图6）

生：爱心。

师：原来小青蛙给我们送了一颗爱心，仔细看，这颗爱心是我们学过的什么图形？

生：轴对称图形。

师：而且它的对称轴很明显。（2，4）（4，2）（5，7）（7，5）有意思吧？哇，原来我们可以根据数对描出点，并连成图形。

数、形不分家，而如何巧妙地从数到形，周老师及其团队充分利用数对的特点，将小青蛙捕虫轨迹由点呈现，由线成图，用线画出来，这样形成了金鱼图，由金鱼图衍生出爱心图。学生在动手操作的描点过程中，脑中并非空空，而是一直努力思索揣测着图形可能的样子，并通过图进一步巩固对数对的认知。而有些学生一开始描点错误后，得不到爱心图，通过图的显现，学生在这一画图操作过程中，自主调整、改善，进而发现找错的数对。使学生达到“内化于心、外化于形”的效果。

三、大胆想象，提升思维

黑格尔说：“真正的创造就是艺术想象的活动。”想象中有创造的萌芽，由想象产生疑问，从疑问开始探索，使儿童产生自觉创造的可能。由于想象不稳定、转瞬即逝，对于严谨的思维而言是不可靠的导向。然而，在假设形成阶段，想象出的图像可以激发对创造力有用的模式。学生对于某些事物产生奇特的想法或看法，其中不乏一些新创意、新思路。

[片断三]

师：数对我们可以给它加着玩，减着玩。还可以怎么玩？

生：乘、除。

師：如果给数对的每个数都乘一个相同的数。图形又会怎样？

生1：面积不变，周长不变，但位置移动。

生2：我觉得面积变了，周长变了，位置不变。

生3：我觉得它的面积、周长、位置都变了。

生4：我觉得面积不变，周长不变，但位置是变的。如果乘的话，位置会向右上方平移，除的话会向左下方平移。

师：那到底会怎样，试一下吧？请同学们拿出练习纸2。请你们将每个数对的两个数都乘一个相同的数，看画出来的图形会怎么样？

生开始找点，连线。

师：看看陈昭希同学的作品。来说说，你发现了什么？（如图7）

生：位置、大小、面积、周长都变了。

师：梁浩楠同学的作品，你发现了什么？（如图8）

生：周长、面积、位置都会变。

师：两张放在一起。你有什么发现吗？（如图9）

生1：如果乘的数越大，面积也越大，位置相比原来也会越远。

生2：发现边长乘几，边长就是几。如果边长乘a，那么现在三角形的面积是原来三角形的a2倍。

师：哇，你都发现现在三角形和原来三角形面积的倍数关系了。对呀，面积、位置都变了，有什么是没变的吗？

生：三角形的形状没有变。

师：通过我们的探究发现，三角形面积会变大，而且位置也会越来越远。如果这张纸足够大的话，三角（下转126页）（上接118页）形会不会更大，更远？利用数对，就让数和形紧密地联系起来了，以后的学习当中，我们可以利用数来研究图形，反过来，利用图形来探索数。

“如果给数对的每个数都乘一个相同的数。图形又会怎样？”学生对此问题的回答，需借助想象，具有一定的创新性，是学生在思考知识外延基础上个性化地衍生出的奇思妙想。陶行知先生说过：培养儿童的创造力，首先要解放他们的头脑、双手、嘴、空间、时间，并且给予充分的营养。在上述过程中，通过数对乘一个数，想象之后的图形会怎么样？提供了多种可能，学生在面积、周长、位置关系中进行阐述，想象之后的验证让人佩服，学生凭借想象，思维飞了起来，数学智慧得以提升。

众多科学和心理学研究表明：创造力是可以培养的，而儿童时期又是一个人的非常特殊的一个阶段，其大脑发育的爆发性与创造力的培养需要更多的关注。先前所受的大部分教育隐含地告诉儿童，数学上的正确答案只有一个。而事实并不是这样的，本课的设计初衷就是开放数学思维，学生通过自己的合理猜想、画图操作、大胆想象、勇于创新，对用数对确定位置的核心与外延有了质的飞跃。

参考文献：

[1]吉姆·兰德尔.创造力——跳出盒子的思维[M].张潇予，译.上海：上海交通大学出版社，2017.

[2]托马斯L·萨蒂.创造性思维改变思维做决策[M].石勇，李兴森，译.北京：机械工业出版社，2017.