结构化视角下数学深度学习的实践探究

摘   要 深度学习在认知领域学习目标分类中对应着记忆与理解、应用与分析、评价与创造等多个层次，需要学生在理解的基础上，批判性地学习新的思想和事实，并融会贯通纳入自身认知结构中。适时提出深度学习，既是学习规律的客观需求，更是主动面对信息时代挑战的积极回应。数学深度学习立足于结构化的数学课程观，在教学实践中强调兼顾知识结构化生成、立足思维高阶化发展、促进问题策略化解决以及立德树人持续化生长。

关键词 深度学习  结构化  高阶思维  策略化  立德樹人

深度学习又称深层学习，是关于学习层次的重要概念。1976年美国学者FerenceMarton和Roger Saljo率先基于学生阅读实验，相对于孤立记忆与非批判性接受知识的浅层学习而提出这一概念。2014年9月，中国教育部基础教育课程教材发展中心主持“深度学习”教学改进项目并正式运作，开启了中国探索促进学生深度学习的重要历程。

一、数学深度学习的价值

深度学习认知水平不仅包括记忆与理解，还涉及应用与分析、评价与创造等多个较高等级的维度层次，以及更加注重知识的应用和问题的解决。在数学教育教学实践中，深度学习需要学生在理解的基础上，学会批判性地接受新的数学事实和思想并融会贯通纳入自身认知结构中。即面对海量信息，学生要从进行理解与联系出发，学会批判与构建，尝试迁移与应用到新的情境中，最终正确作出决策并解决问题[1]。教学指向“深度学习”，其意义在于：既引领积极参与，更注重知识的系统化传递;既重视激发学习乐趣，更注重学习能力的形成;既追求师生合作愉悦，更强调德育的培塑，最终更好地促进学生形成学习能力，秉承学科素养，追求品质价值[2]。数学深度学习着眼于结构化的数学课程观，可以为学生提供数学整体认识观，从而有效促进学生从整体上把握数学知识、方法和观念;又与过程性原则相辅相成，使得发现式、开放式学习“有章可循”;还能更好地促进学生形成从已知向未知迁移的倾向性，真正提高数学学习的可持续发展性。

二、数学深度学习的实践策略

2019年6月，中共中央、国务院印发《关于深化教育教学改革全面提高义务教育质量的意见》，强调落实立德树人根本任务，树立科学的教育质量观念，提出了全面提高义务教育质量的主要任务，强化课堂主阵地作用，要求优化教学方式，注重启发式、互动式、探究式教学[3]。显然，为达成上述目标，必须从深度学习的视角调整我们的课堂教学行为。

1.深度理解——从关注知识传授转向兼顾知识结构化生成

数学课堂中教师不能仅是传授知识，而应紧紧围绕教学要求和目标，在结构化观念指导下“注重基础，削枝强干”，紧扣重点与难点，卡准关键点，着力挖掘、理顺教学内容主线。同时应尽量凸显“高观点、低起点”的课程安排结构特点，鼓励学生探究，关注课堂对话与留白，让数学学习内容与认知规律和学生的最近发展区相适应、与教学方式相匹配，真正促进学生的深度理解。

案例一 “圆周角”概念的生成[4]

活动1 设置结构化情境，温故探新。

回顾我们前面学习的与圆有关的一种角—圆心角。圆心角是怎么定义的？

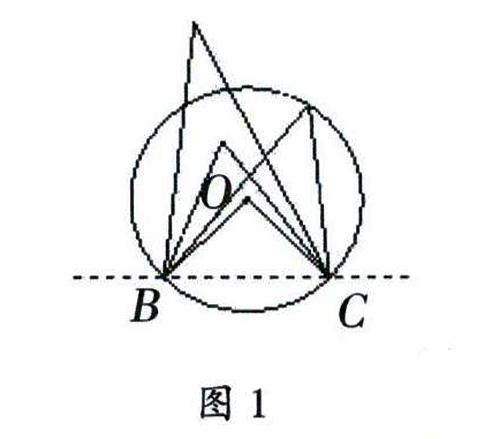
动手操作：在所给的⊙O中，请画出劣弧所对圆心角（如图1）。

若B、C固定不动，改变所画角的顶点位置，确保新的顶点仍与点O保持在BC同侧，观察新顶点与⊙O的位置关系，可分为哪几类情形？

[设计意图]从知识结构出发，作为新知诱发阶段，选择关联知识的切入点，既快速有效再现认知基础，又激发学生介入新知的兴趣。这样的设计既潜移默化复习强调圆心角概念和性质，又水到渠成引领学生获取经验将圆心角的研究方法迁移到新知学习中，自然产生探究新知的欲望。

活动2 揭示生成性概念，体验建构。

观察呈现出的三类角（见图1），按照从特殊到一般的研究策略，重点关注顶点在圆上的角，归纳其位置特征，并尝试命名。

[设计意图]在概念生成的关键环节，促使学生参与意识从潜伏状态转为活跃状态，认真观察，自主思考，想象创造，尝试下定义，培养合作精神，使学生真正经历知识的发生、探索、生成过程。

本案例从学生最近发展区出发，依照数学知识间的结构联系，由图索思，激发学生的好奇心与探知欲。而通过操作、观察、合作，进一步从多角度完善了对图形运动的理解，全过程既注重直观，又与合情推理有机结合，把几何抽象发现作为探究活动的自然延续和必然发展，自然生成式的建构体验，让学生充分感受到数学学习的有趣性和丰富性。

“兼顾知识结构化生成”的教学重视数学知识的发生、发展、提升等基本过程，多采用“概念变式”“图形变式”“过程变式”等策略，强调数学概念的多角度生成与理解。其操作要义包括：创设适切的较为直接的情境、问题，预设阅读、观察、探究、交流等活动，让学生较充分地经历数学概念的概括和抽象过程，数学原理的推导和归纳过程，理解数学概念的生成性，积累数学活动体验和经验[5]。

2.深度思考——从关注学生参与转向立足思维高阶化发展

高阶思维是高阶能力的核心，自然也是深度学习的重要着力点，主要涉及创新能力、问题求解能力、决策力以及批判性思维能力等，集中体现了信息时代对人才素养提出的新要求，也是个体适应时代发展的关键能力。

案例二  生活中的数学智慧——学会退回到最简单的情形[4]

设计游戏：一长方形平整桌面，两人相继轮流往上放置形同的硬币，硬币要求平放，且后放的硬币不能压在先放的硬币上。如此继续下去，桌面上只剩下放置一个硬币位置时，谁放下最后一枚即为获胜者。

当遇到一个难以下手的困难问题时，可以采取退的方法。这样的“退”，往往能使我们获得方法上的帮助。退的最终目的是为了进，这种策略称之为“先退下而后跃上”。可从一般退到特殊，从抽象退到具体，从复杂退到简单，从整体退到部分，从高维退到低维，从较强结论退到较弱结论，一直退到保持特征的最简单的情形。以退求进策略的具体表现包括取值、极端、特殊化、由试验而归纳等。

“立足思维高阶化发展”的教学注重数学思想方法的渗透，而相关数学思想往往蕴涵在数学知识的发生、发展、应用等过程中，是相关数学知识方法在更高层次意义上的抽象与概括，譬如分类、演绎、抽象、归纳等。学生通过独立思考、合作交流，可以在积极参与数学学习的活动中逐步感悟内化数学思想方法，从而迈向思维的高阶化。

3.深度迁移——从关注解题教学转向促进问题策略化解决[6]

当今社会正处在一个多元而高速发展的时代，教育必须担当起培养具有问题解决能力人才的任务。掌握基本的学习策略是衡量学生是否学会思考、是否能持续发展的显要標志;问题的策略化解决，也是促进学习者自身认知发展的重要路径。

案例三  人教版八年级课题学习“最短路径问题”

教材编排了“牧马饮马”与“造桥选址”两个问题，各自独立，无从体现整体性，同时“造桥选址”问题属于非常规性解决思路，绝大多数学生无法直接解决。我们可尝试将这两大问题“合二为一”，设置成统一背景的问题链，有效增强整体性，利于学生识别问题模型，形成解决策略。

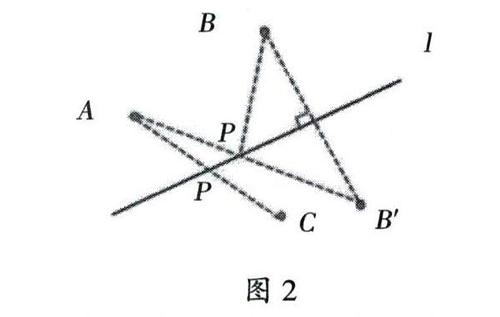
创设问题背景：某勘测队到近似笔直的河流l两侧勘测，为方便，在l两侧共设置了A，B，C三个勘测点（如图2）。

活动1  现拟在A处建一蓄水池，从河岸引流水到蓄水池，则应在河岸何处开挖，能使水渠的长度最短？画图并说明理由。

[设计意图]首先设置了一个单点到直线的最短路径问题，简单自然而易于解决，调动学生参与的积极性，同时也奠定了整个问题链的设置基调，便于学生后续模仿和正向迁移。

活动2  仿照活动1，利用已有相关知识设计一个类似的问题，并在小组内寻求解答。

[设计意图]给出简单明晰的操作要求，强化学生提问题的意识，促使其自觉地运用储备知识，尝试自主设置问题，并学会评价他人方案的可行性。

活动3  变式：忽略河流宽度，要在河岸何处开挖，能使得该处到A，B所挖水渠长度之和最小？画图并说明理由。

[设计意图]变式问题已演变为在直线上找一点，使其到直线同侧两点距离和最小，这即为原教材中经典最短路径问题模型。

“促进问题策略化解决”的教学重在培育学科素养，发展学生能力。数学问题解决不等同于数学解题，它是在特定问题情境中，按照一定的目标，合理应用数学概念、原理、技能与方法等，经过多重操作使问题得以解决的策略化过程。平时教学中可多尝试“单元结构化教学”的形式，基于单元开展活动设计，不断充实教学资源和经验，促进学生数学问题解决策略化的形成。

4.全面育人——从关注教学效果转向立德树人持续化生长

深度学习的终极目标之一是促进“人”的发展，这与中国基础教育学科育人目标的演变是指向一致的，即从双基，到三维目标，再到核心素养。教育部在《关于全面深化课程改革落实立德树人根本任务的意见》中，明确提出要关注并发展学生的核心素养[7]，这将是教育改革长期的必然走向和趋势。要通过初中数学深度学习提升学生核心素养，就应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想，此外，还应特别注重发展学生的应用意识和创新意识。

立德树人指向教育的全方位视角，提出了“培养什么人”与“怎样培养人”的深刻主题。这一根本任务既有对教育者的要求，也是对被教育者的期待。因此，必然要给予师生双方互动的渠道与途径，也就必然要求教者在课堂教学过程中要做到因地制宜、因材施教、灵活机动。立德树人是一个结构化的系统工程，要把教育的育人功能与学校的文化特色建设联系起来，与整个社会的硬、软环境结合起来，而不是仅仅片面追求升学率，只注重结果而忽视过程的生长性。

“立德树人持续化生长”的教学重视教师引领下学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展。在这样的过程中，学生掌握学科的核心知识，理解学习的过程，把握学科的本质及思想方法，形成积极的内在学习动机、高级的社会性情感、积极的态度、正确的价值观，成为既具独立性、批判性、创造性又有合作精神、基础扎实的优秀学习者，成为未来社会历史实践的主力军。

三、对数学深度学习的反思

1.择善而收，在超限与拓展间寻求平衡

在课程建设中最主要的两个方面是学科课程体系和学生身心发展规律，教学活动必须以此为依据持续、连贯地开展。而追求课程结构体系的相对完善必然会带来“超标超限”的风险。这就需要教者理智地处理好二者间的平衡，切莫为追求结构化而走向另一个极端，必须切实考虑到学生的学情基础，以及初中数学课程的基础性与普及性。

2.适切引领，在结构与过程中提升素养

教育既要适应时代的现实需求，又要着眼于学生更全面、更长远的发展。教师必须摈弃狭隘的课程观，并以最适合的方式引领学生。结构化的数学课程理念昭示了数学课程设置的基本目的，即在学生获取数学基础知识、技能与方法之外，还应让学生理解数学，学会用数学的理性眼光去观察、认识自己所生活的世界，在数学课程的系统中以及教学进程中进一步形成数学核心素养，发展创新意识和实践能力，最终落实立德树人根本任务。

参考文献

[1] 何玲，黎加厚.促进学生深度学习[J].现代教学，2005（05）.

[2] 郭华.深度学习及其意义[J].课程·教材·教法，2016（11）.

[3] 中共中央国务院.关于深化教育教学改革全面提高义务教育质量的意见[Z].北京：人民出版社，2019.

[4] 吴小兵.初中数学课堂教学的20个细节[M].南京：南京师范大学出版社，2016.

[5] 刘达，黄华.向世界展示中国的数学教育智慧——义务教育阶段数学课程改革的“上海经验”[J].人民教育，2019（3/4）.

[6] 吴小兵.寻“路”探“径”，“策略”先行[J].中小学数学：初中版，2018（12）.

[7] 中华人民共和国教育部.教育部关于全面深化课程改革落实立德树人根本任务的意见[Z].2014-04-08.【责任编辑  郭振玲】

该文为江苏省教育科学“十三五”规划重点自筹课题“促进初中数学课堂深度学习的校本行动研究”（Eb/2018/08）的阶段性成果