离散力学与最优控制理论在谐波减速器控制中的应用研究

陆 铨，冮铁强，陈立杰

(厦门大学航空航天学院，福建厦门 361005)

1 引言

谐波减速器在航空航天领域有着广泛的应用，如何设计控制策略、解决谐波减速器内部非线性干扰问题是其应用中的一个难点。目前，谐波减速器的建模与控制研究主要基于连续时域。如Tuttle[1]研究了谐波减速器在摩擦损失、柔性阻尼等非线性特性影响下的细分模型。Han 等[2]设计了基于电机角位置和卡尔曼滤波器的角加速度估计器，采用改进前馈补偿控制器来补偿非线性摩擦，但该控制器缺乏稳定性证明。Ding[3]通过仿真发现，线性滑模控制器在到达滑模面之前对摩擦干扰非常敏感，使用二次积分滑模面能在一定程度上提高控制器的鲁棒性，但该控制器的性能指标十分保守。可见连续时域下控制器的性能与稳定性证明问题受制于系统模型的复杂度，而离散时域下的建模与控制能提供新的研究方向。

对于非线性系统的离散，传统方法为局部线性化。如Maes[4]、Diao[5]等分别使用一阶欧拉法和二阶欧拉法计算了线性时变系统的传递函数矩阵，但这两种方法需不断重新计算系统的传递函数矩阵；Han 等[6]基于系统的局部传递函数矩阵设计了模型参考自适应控制器，使用Popov 超稳定性理论保证了控制器的稳定性，但该算法对控制器的实时计算能力要求较高。上述离散控制研究均基于连续时间系统模型，离散精度与控制器性能均不理想。为此，本文将离散力学与最优控制理论应用于谐波减速器的控制研究，在不使用连续时间模型的前提下，考虑柔性关节与粘性摩擦，建立全时域离散模型，研究谐波减速器的最优轨迹控制与最优时间到达问题。

2 谐波减速器的离散时间建模

研究对象为一对由伺服电机和谐波减速器组合而成的串联驱动系统，其模型见图1。该系统有两个自由度，分别为谐波减速器的输出轴转角θl和电机转子的输出转角θm；伺服电机通过转子输出扭矩u，谐波减速器的输出端带有负载。

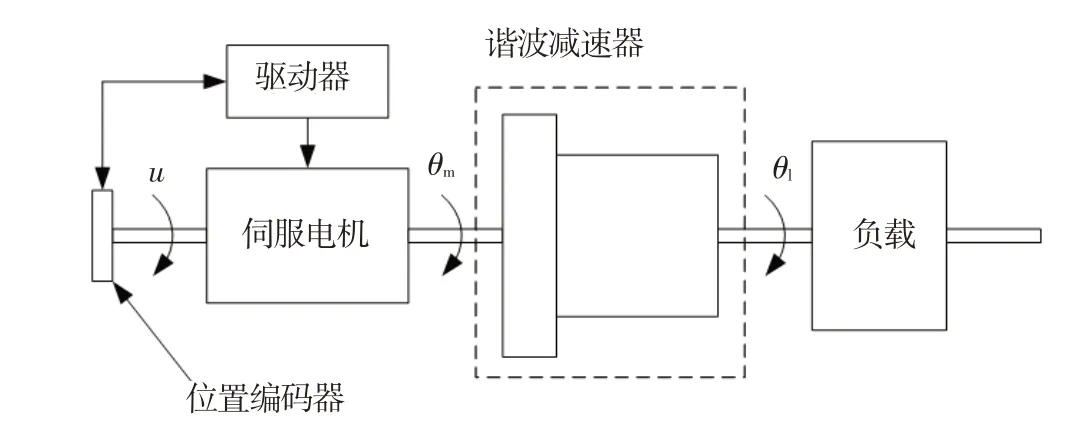
图1 谐波减速器驱动系统模型简图Fig.1 Diagram of harmonic drive transmission system

为平衡计算效率与模型精度，本文所有的近似方法均选择中点法。谐波减速器传动系统的拉格朗日函数构造为：

根据文献[7]中的离散Lagrangian-d′Alembert原理，可得到任意时间区间[kh,(k+1) h]内的等价离散拉格朗日函数为：

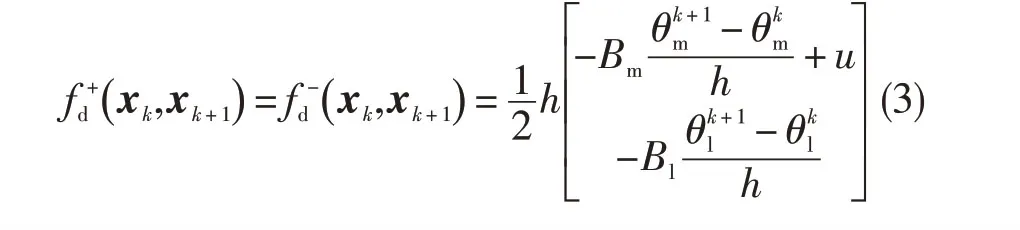
式中：Bm为伺服电机内部的粘性摩擦系数，Bl为谐波减速器内部的粘性摩擦系数。

将式(2)、式(3)带入文献[6]中的离散拉格朗日方程，可得到用代数方程表示的谐波减速器离散模型：

式中：k=1,2,3…,n-1。

初始点与终点的约束为：

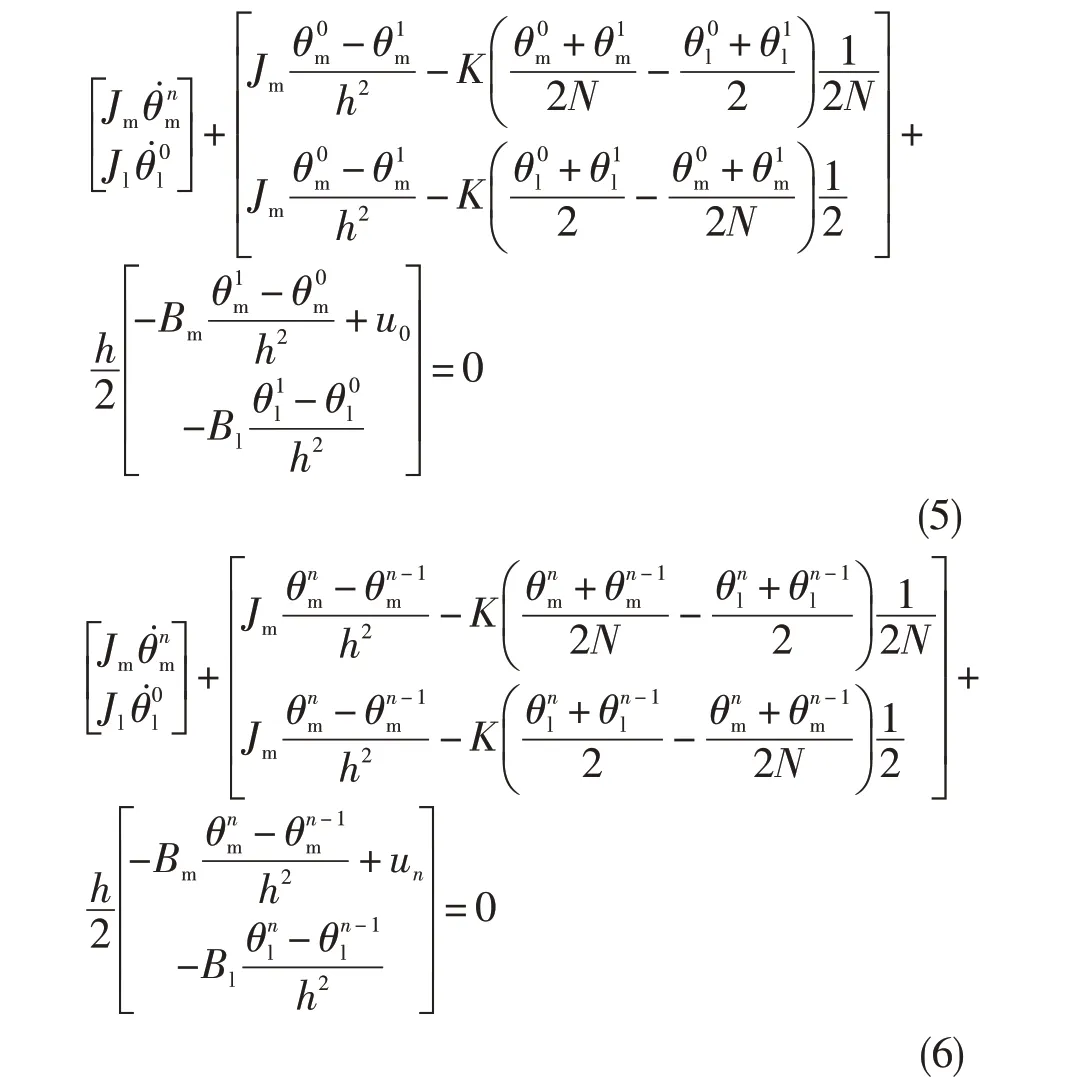
对于上述模型，根据具体控制任务的要求，可以确定系统的总运动时间为T，同时确定系统模型在t=0 时的初始状态为，在t=T 时的末端状态为。该模型的使用可以使多体动力系统控制任务的数学表述式更清晰与简便。从离散模型的建立过程看，本文没有使用经典拉格朗日方程强行求解该系统的连续时间解析解；但是对于任意时间区间，该离散模型的形式仍然恒成立。同时，中间法的使用消除了离散模型中可能出现的导数形式，极大地降低了原连续时间模型的复杂程度。

3 谐波减速器的最优控制

3.1 最优跟踪

最优跟踪问题是指设计控制率使得系统的实际输出y(t)能够跟踪期望轨迹r(t)，同时使指定的目标函数取得极小值的过程。首先需要定义离散时间下最优跟踪问题的目标函数，常用的连续时间最优跟踪性能指标为：

式中：M 和R 均为恒正的权重系数。

对上下限固定的积分号进行等价离散，得到离散时间目标函数：

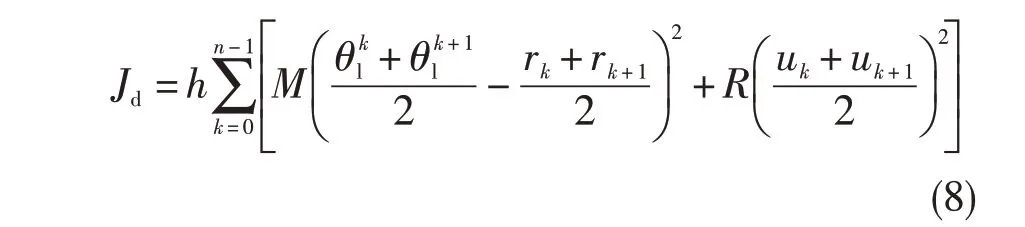
数值实验发现，减小R 或增大M，都可以增加被控系统的输出精度。因此，将最优跟踪问题用下列公式描述：

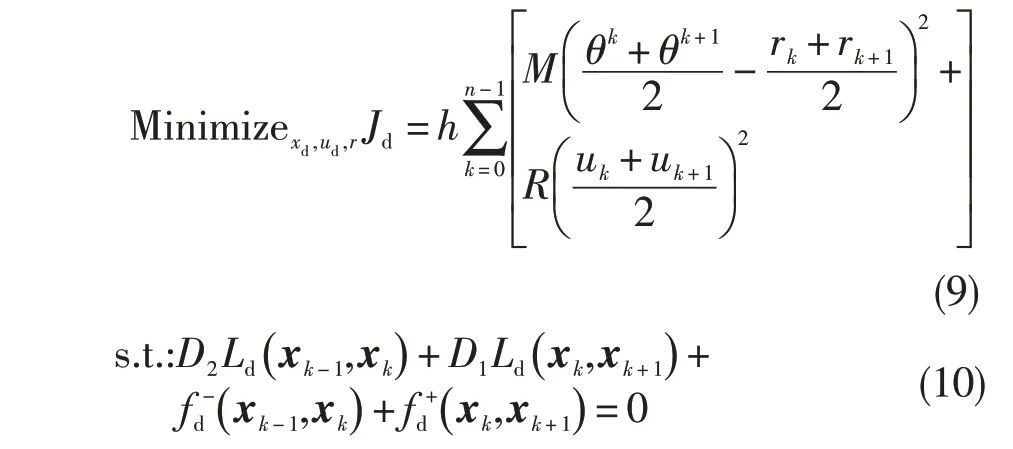
图2 h=0.14 s时离散时间控制下的最优跟踪效果Fig.2 Optimal tracking effect under discrete-time control with h=0.14 s

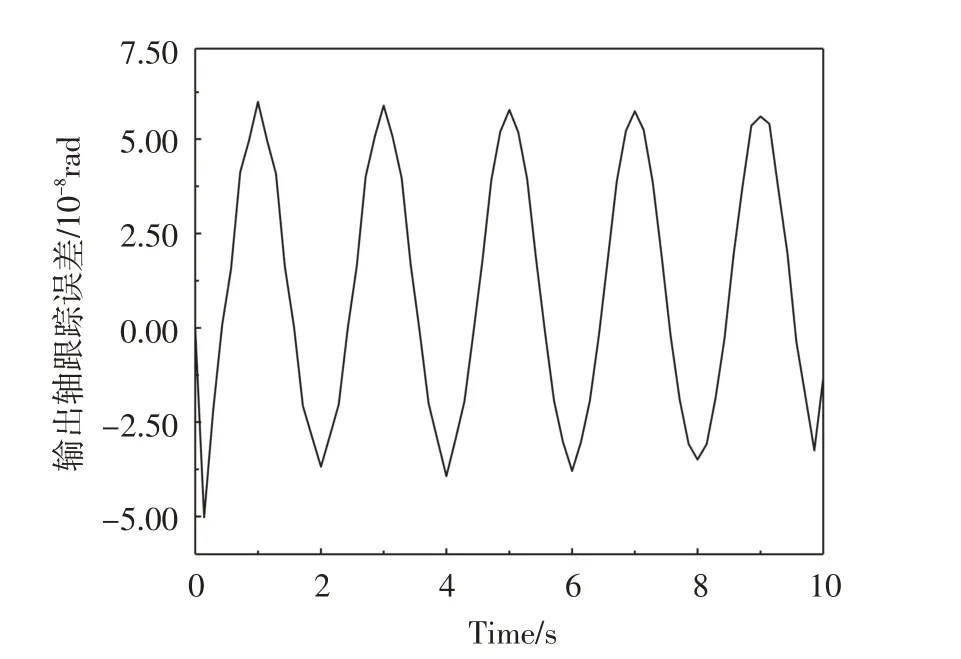
图3 h=0.14 s时的最优跟踪误差Fig.3 Optimal tracking error with h=0.14 s

3.2 时间最优控制

使一个系统的性能指标从初始状态转移到目标集，用时最短的控制率称之为时间最优控制。Shareef等[9]在三角臂机器人上应用了离散最优控制方法，其机械臂在实现最短时间运动的同时还能在起点和终点处均保持零角速度，且离散最优控制方法的求解耗时比相平面法[10]和动态规划法[11]的短。

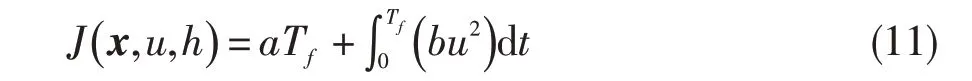
定义连续时间下最速到达问题的目标函数为：式中：Tf为控制时域的长度，a 和b 均为正定的权重系数。

考虑到运动轨迹的光滑性与寻解难度，对上述目标函数进行等价离散，得：

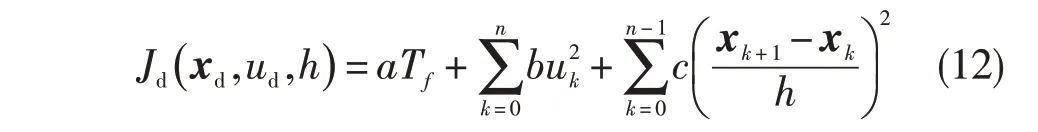
从物理意义上看，式(12)依旧为对最速到达问题的数学描述，通过调整恒正的权重系数a、b 和c的大小，根据具体的控制任务在控制力矩和运动总时间之间权衡。对于起点与终点同时具有严格约束的最速到达问题，使用以下方程组进行描述：

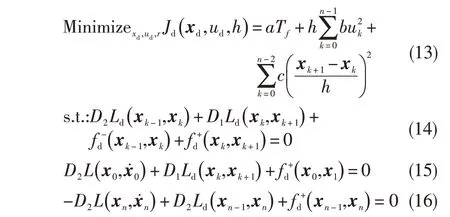
式中：n 为系统模型离散点的个数。

离散时间最优控制所需的系统初始状态为x0=[0,0,0,0]T，系统末端状态为xn=[0,200π,0,4π]T，即谐波减速器从完全静止开始旋转两圈，系统的初始速度和终点速度均为0；假设控制力矩的输出饱和极限为±1 N·m。图4为仿真得到的谐波减速器最速到达曲线。全运动时间约为5.6 s，整个运动过程分为三个阶段，在起始点附近控制系统先使用较小的控制力矩保证平滑启动，之后迅速切换到接近饱和输出状态，使谐波减速器保持匀速运动，并在邻近终点时利用一个反向力矩减速，保证到达速度为0。图5示出了输入轴力矩信号随时间变化的过程。可看出离散控制方法对这三个阶段的时间规划，其中谐波减速器的零速度平滑启动与终点处的零速度平稳到达均使用了很短的调整过程，同时控制信号在整个控制时域中的极值均限制在了±1 N·m以内。

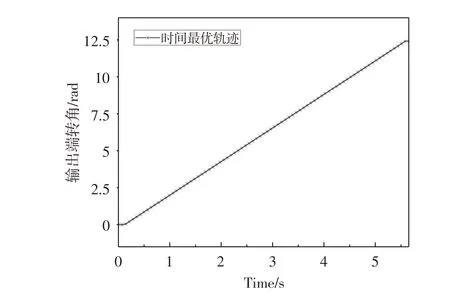
图4 谐波减速器最速到达曲线Fig.4 Time shortest curve of harmonic drive

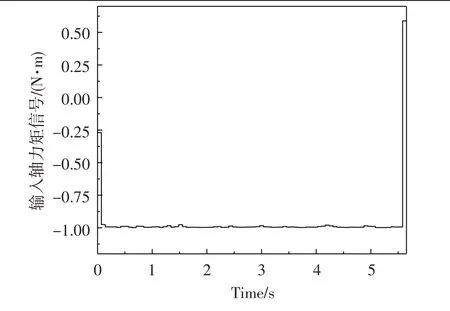
图5 控制力矩信号随时间变化曲线Fig.5 Control torque signals curve with time domain

4 结论

对离散时域下谐波减速器的建模与控制进行了研究，结论如下：

(1) 考虑谐波减速器固有的柔性关节与粘性摩擦特性，在不使用原连续系统模型的前提下建立了全时域离散模型，且该模型代数方程组的表达形式大大降低了系统的复杂度。

(2) 在离散模型的基础上实现了谐波减速器在离散时域下对于复杂轨迹的跟踪能力，且控制系统的调整阶段明显缩短，在全控制时域基本实现了10-8rad量级的跟踪误差。

(3) 对于起始点与终点均具有运动约束的控制任务，离散时间控制通过对不同运动状态的时间规划，在控制力矩具有输出极限的条件下实现了谐波减速器的最短时间控制。