水滴型凸肋通道内流动换热的数值模拟*
2020-06-19胡艺凡闫子豪熊心悦
杨 超,胡艺凡,闫子豪,莫 奇,熊心悦,许 玉
(南京航空航天大学,飞行器环境控制与生命保障工业和信息化部实验室,江苏 南京 210016)
随着微电子技术的快速发展,微流动系统在高热流密度微型器件的散热中应用的越来越多。作为微流动系统的重要组成部分,微通道换热器因具有较好的强化换热效果,得到了广泛关注和研究,并发展出强化换热效果更好的凸肋换热器。
为了研究凸肋换热器,国内外学者开展了一系列相关研究。Kosar等[1-3]对大长宽比微通道内的单相流动的阻力和换热特性进行了研究,发现宏观尺度下的计算关联式不再适用微尺度流动换热。此外,凸肋换热器在高热流密度条件下,可以保持换热表面温度低于70 ℃,并且对凸肋进行设计可在不降低换热效果下有效减小流阻。Shah[4]对微通道内的流阻进行了研究,并基于大量实验数据提出了摩擦因子(f)与通道长宽比的关系式。Naphon和Wiriyasart[5]针对CPU散热,采用铜和铝两种材料,对6种不同凸肋换热器的冷却性能进行了对比分析。Xu和Wu等[6]研究了矩形和方形凸肋在顺排和叉排时的流动换热特性,发现叉排在增大阻力的同时强化换热。夏国栋等[7]对圆形凸肋的高径比进行了研究,发现在相同工况下,圆形凸肋长径比是影响摩擦因子和换热特性的主要因素之一。Patil和Dingare[8]发现凸肋与来流方向夹角为0°时换热系数最高。杨宇辰等[9]通过研究不同孔隙率的圆形凸肋,发现孔隙率较小时,热流密度对凸肋通道的努塞尔数(Nu)影响不大,孔隙率较大时,热流密度升高,Nu升高。
在此基础上,针对凸肋形状的优化研究还相当有限。如Prasher等[10]对圆形和方形凸肋叉排时的流动和换热特性进行了研究,得到了f和Nu在Re=100左右均发生转折,因而它们与Re的对应关系在此处亦变化。Wu等[6]对矩形、圆形、椭圆形凸肋进行大量实验研究,总结出了Nu的经验公式。Sakanova和Tseng[11]设计了两种翼型凸肋并与圆形凸肋对比,得到了性能较好的肋片结构。
总的来说,目前凸肋换热器的研究大都集中在圆柱型和矩柱型等肋片结构,鉴于尾涡滞留区的产生,流动和换热效果有进一步提升的空间。作为一种新型的结构,水滴型肋片对通道内流动和换热特性的影响亟需揭示。
1 数值模拟
1.1 物理模型
本文数值模拟采用的物理模型如图1所示。通道长L=25 mm、宽W=2.4 mm、高H=0.11 mm。工质为水。水滴型凸肋前部半圆直径均为0.1 mm,尾缘角度α分别为25°、30°、35°和60°。此外,建立圆柱型凸肋(直径0.1 mm)和无凸肋通道模型作为对比。水滴型和圆柱形凸肋高度均为Hfin=0.08 mm,凸肋顶端与通道壁面未接触,存在一定间隙。
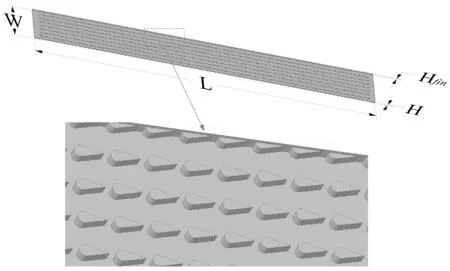
图1 物理模型Fig.1 Physical model
不同通道中凸肋的具体尺寸列于表1,其中SL为凸肋横向间距,ST为凸肋纵向间距,Lfin为凸肋长度,布置方式均为顺排(图2)。

表1 凸肋几何尺寸Table 1 Geometric sizes of pin-fins
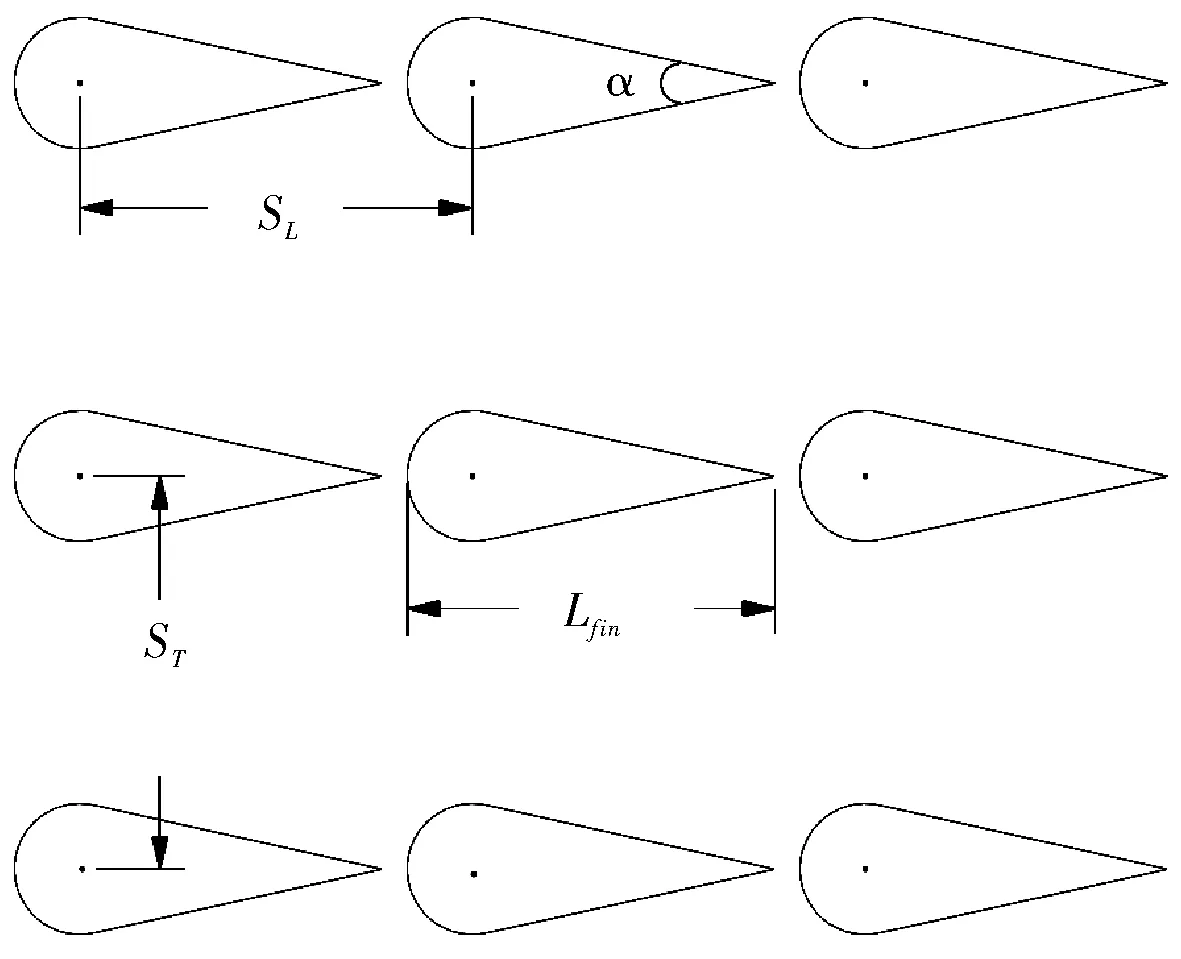
图2 凸肋布置方式Fig.2 Arrangement of pin-fins
1.2 数学模型
为使微尺度凸肋通道内的流动和换热模拟更易收敛,作出以下假设:流体工质不可压缩,忽略热辐射效应,热物性不随温度变化,边界无滑移,材料各向同性。
由于本研究涉及流固耦合问题,控制方程由流体区域的连续性方程、动量方程、能量方程以及固体区域的能量方程组成:
·ρfu=0
(1)
ρf(u·u)=-p+μf2u
(2)
ρfcp(u·T)=λf2T
(3)
λs2T=0
(4)
式中:ρf为流体密度,kg·m-3;u为流速,m·s-1;μf为流体动力粘度,Pa·s;cp为流体定压比热,J/(kg·K);λf为流体导热系数,W/(m·K);λs为固体导热系数,W/(m·K);p为压力,Pa;T为温度,K。
采用速度入口、自由流出口、无滑移壁面等边界条件,通道底面为加热面,热流密度为360 kW·m-2,其他壁面均绝热。初始时刻,进口温度为303.15 K。
1.3 网格划分和验证
利用ICEM对凸肋通道的物理模型进行非结构网格划分,并在凸肋及其附近加密(图3)。

图3 局部网格Fig.3 Partial meshes
为了保证计算结果的准确度,同时节省计算时间,又进行了网格无关性验证。选取3种数量的网格,对比各网格量下的通道进出口压降和温差,结果列于表2。

表2 网格无关性验证Table 2 Independence verification of meshes
从表2中可以看出,与2765820网格相比,862504网格的压降和温差的误差分别为1.3%和2.0%,1937112网格的误差为0.8%和1.4%。因此,本研究选用1937112网格,既可达到足够精度,又可提高计算效率。
1.4 计算方法
利用Fluent进行模拟。开启能量方程,选择层流模型,压力-速度耦合采用SIMPLE方法,松弛因子保持默认值。模拟中,在通道入口、入口后0.8 mm、中部、出口前0.8 mm、出口、加热底面和整个流场设置多处监控器,用于判断收敛情况。残差标准设置为10-5。
1.5 数据处理
在微通道换热器流阻与换热特性研究中,特征参数根据换热器形状按照管束式计算方法来分析,即特征长度取微通道的水力直径Dh:
(5)
雷诺数Re定义为
(6)
式中,uin为入口流速,m·s-1。
通道进出口压降Δp定义为:
Δp=pin-pout
(7)
式中,pin为通道入口压力,Pa;pout为通道出口压力,Pa。
通道换热系数h定义为:
(8)
式中,q为加热面热流密度,kW/(m2·K);Tw为加热面平均温度,K;Tl为流体平均温度,K。
通道努塞尔数Nu定义为:
(9)
通道压降按下式计算:
(10)
式中,f为Darcy-Weisbach摩擦因子。
对于矩形通道内的层流流动,f可按Hartnett和Kostic[12]提出的的多项式简化方程计算:
fRe=96(1-1.3553γ+1.9467γ2-1.7012γ3+0.9564γ4-0.2537γ5)
(11)
式中,γ为矩形微通道截面高宽比。
报案称,2018年2月15日22时30分,在吉林省敦化市××小区,一幢没有保暖设备的车库起火,一辆黑色奥迪A6L及库内物品损毁。
2 模拟结果
2.1 模拟方法可靠性验证
为了验证本文数值模拟方法的可靠性,对Xu和Wu[6]实验中的微凸肋换热器进行模拟,并将模拟结果与实验数据进行对比(图4)。从图4中可以看出,在各个Re下,模拟压降与实验压降均十分接近,因而,可以认为本文的数值模拟方法有效。

图4 压降模拟值与实验值对比Fig.4 Comparison of numerical and experimental pressure drops
2.2 凸肋通道流动特性
流体进入通道后,首先在空白通道中均匀流动,随后进入有凸肋部分,此时流动截面积迅速变小,速度迅速增加,流体撞击凸肋前端面后沿着凸肋二次分离,并在此凸肋后方汇合形成尾流区,然后再次撞击下一排凸肋,如此反复,直至最后一排凸肋。
如图5所示,N2(圆柱)和N3(α=25°)通道的压降明显大于N1(空白)通道的。当Re>400时,N3(α=25°)通道的压降比N2(圆柱)通道的小,且随Re的增大,改善越来越大。这说明水滴型凸肋相对于圆柱型凸肋,具有一定的减小流动阻力的作用,因为尾翼的添加可以改善流体绕流后的流动状况,而且Re增大后,圆柱型凸肋尾部因旋涡脱落而产生的压降进一步增大,而水滴型凸肋仍能抑制此种压降。

图5 N1、N2和N3通道的压降Fig.5 Pressure drops of N1, N2 and N3 channels
如图6所示,N4(α=30°)和N6(α=60°)通道的流动特性与N2(圆柱)相比较都得到了一定改善,且随着Re的增加,改善相对更明显。但是,由于N4(α=30°)通道的凸肋拥有过长的尾翼,绕流后的流体不能充分地再次汇合就撞击在后方凸肋前缘,因而N4(α=30°)通道的压降高于N6(α=60°)的,N6(α=60°)通道拥有更好的流动性能。

图6 N2、N4和N6通道的压降Fig.6 Pressure drops of channels N2, N4 and N6

图7 N3、N4和N5通道的压降Fig.7 Pressure drops of N3, N4 and N5 channels
如图7所示,N3(α=25°)、N4(α=30°)和N5(α=35°)通道的压降在Re<400时几乎相同,α对流阻的影响不大。当Re=700时,N4(α=30°)通道的压降与其他两者有较大差值,此时流动特性最好的为有最长尾翼的N3(α=25°)通道。
2.3 凸肋通道换热特性
如图8所示,水滴型凸肋(N3)改善了尾流区的换热特性,有效地强化了通道的换热能力。在Re<700时,无凸肋通道(N1)的Nu随Re增加的趋势基本呈线性,并且Re对Nu的影响较小。然而,对于有凸肋通道(N2和N3),Nu随Re的变化趋势更明显。对于水滴型凸肋(N3)通道,Re=100~700,Re越大Nu的增加越明显。具体地,Re=400时的Nu比Re=250时的只增大了6.3,而Re=700时的Nu比Re=550时增大了17.6,说明水滴型凸肋对换热的增强在Re越大时越显著。

图8 N1、N2和N3通道的NuFig.8 Nu of N1, N2 and N3 channels
如图9所示,N4(α=30°)和N6(α=60°)通道的换热能力都远强于N2(圆柱)通道。在较低Re时,N6(α=60°)通道的换热能力强于N4(α=30°)通道的,但二者的差距并不明显。随着Re增加,N4(α=30°)通道的Nu反超过N6(α=60°)通道的,并且上升趋势更剧烈。这是因为Re越大,尾流区越长,α=30°的水滴型凸肋拥有更长的尾翼,能保证绕流后的流体更好地换热。总的来说,在Re=100~700时,α=30°的水滴型凸肋平均Nu更大,换热能力更强。图10展示了N1(空白)、N2(圆柱)、N4(α=30°)和N6(α=60°)通道在Re=550时,出口附近加热面的温度场,从中亦可看出α=30°的换热效果更好。
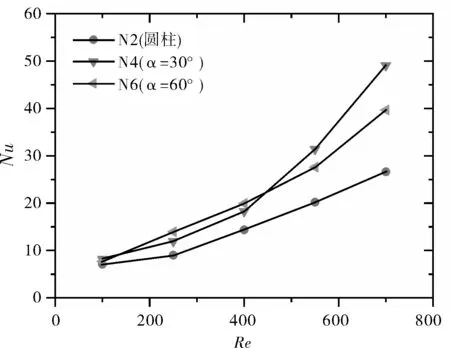
图9 N2、N4和N6通道的NuFig.9 Nu of N2, N4 and N6 channels

图10 N1、N2、N4和N6通道加热面温度场Fig.10 Temperature fields of N1, N2, N4 and N6 channels
如图11所示,N3(α=25°)和N5(α=35°)通道在Re较低时,Nu略高于N4(α=30°)通道的,但在Re较大时,N3(α=25°)和N5(α=35°)通道的Nu则低于N4(α=30°)通道的,且差距随着Re的增大而增大。α=25°和α=35°的水滴型凸肋的换热性能随着Re的增长逐渐变得平缓,而对于α=30°的水滴型凸肋,其增长速率越来越大。
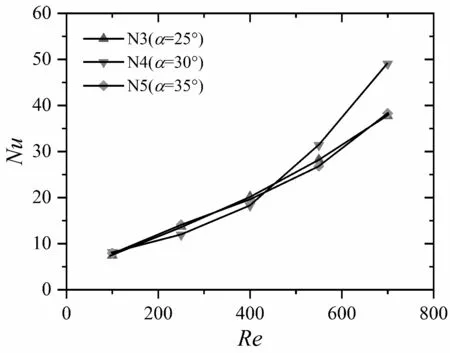
图11 N3、N4和N5通道的NuFig.11 Nu of N3, N4 and N5 channels
3 结 论
本文采用三维数值模拟的方法,对比分析了6种不同通道的流动和换热特性,并得到以下结论:
(1)水滴型凸肋通道的流阻小于圆柱型凸肋通道的,换热性能亦强于圆柱型通道的,具有显著的综合性能优势。
(2)对于水滴型凸肋通道,尾缘角度对流阻的影响相对不明显,而对换热的影响较明显。合理设计水滴型凸肋可以有效提高通道的综合性能。
(3)不同工况存在不同的最佳尾缘角度。当Re=400~700时,α=30°的水滴型凸肋通道为最优解,当Re=100~400时,α=60°的通道为最优解。
